利用气枪声源数据的地声参数反演∗
李佳蔚贾雨晴鹿力成 郭圣明马 力
(1中国科学院声学研究所 北京 100190)
(2中国科学院水声环境特性重点实验室 北京 100190)
(3中国科学院大学 北京 100049)
0 引言
地声反演问题由来已久,且一直是水声学中的热点问题之一。其基本思路为声波通过浅海波导传播时会携带边界上的信息,从而使得通过接收的声场能够间接获取地声参数。Hamilton[1]很早就对各类海底地声属性进行了归纳,获取了各类海底的声学参数范围曲线及参数关系的经验公式。早期的地声反演仅计算与观测量线性相关的地声参数,获取的参数有限。常规匹配场(Matched field processer,MFP)[2−3]的应用使得地声反演得到极大的发展,其主要思想是以某种优化准则建立接收处声传感器阵列测量的声信号与不同海洋参数下仿真的声信号的代价函数,以全局优化算法获取最佳代价函数的参数值为反演值。各类智能优化算法的引入也大幅度提升了计算速度,常见的有模拟退火算法[4−5]、遗传算法、蚁群算法等。
通过接收声场可以获取到不同的声学特征参数,常用于反演的声学特征参数有阵列接收的声压、群速度、模式衰减、模式幅值比、传播损失等。Jiang等[6]在局部区域反演中利用多途信道与声压幅值信息,获得沉积层与基底层声参数信息进行地声反演。李整林等[7]利用简正波过滤技术获取简正波群延时。郭晓乐等[8]利用warping变换提取来获取频散曲线的时间差来反演海底声速与密度。Potty等[9]、Zeng等[10]在各自的文献中均利用模式幅值比来获取海底衰减系数。相比而言,利用传播损失拟合获取海底衰减系数是一种简单易行的方法[8]。不同的声学特征参数对反演海底参数的敏感性不同,利用此原理进行分步反演[11]一方面能获取到最敏感的参数,同时提高计算速率。信号处理的方法能够准确地提取不同的声场特征,其中warping变换的应用较为广泛。Baraniuk等[12]首次将warping变换应用于信号处理,继而被引入到水声信号处理,warping变换通过消除声场瞬时相位的非线性项消除其频散效应。利用warping变换能够实现单声源获取频散曲线[13],分离模态简正波[14]等。
在浅海声学实验中,声源的选择很重要。由于爆炸声源具有源级高、频带宽的特点,常用作各类海洋实验的声源[15−16],其缺点是气泡脉动产生严重干扰,使得获取直达波信号的时长有限,并且由于气泡脉动信号与爆炸声信号的强相关性,基于解卷积[17]、自适应滤波[18]的方法均不能稳定地消除气泡脉动及其造成的影响。气枪声源是利用高压气舱存储的高压气体在水下瞬间释放而产生强声波,它也具有源级高、频带宽的特点,同时气泡脉动影响较小,本文实验选用的气枪声源基本没有气泡脉动的影响。这样用单个水听器就能获得声源信号的时间数据,还可以得到更多的频率数据。在进行地声反演时,本文采取以下措施来降低反演参数的误差:(1)在数据处理时,利用不同的声学特征参数对反演海底参数的敏感性不同进行分步反演,同时它能够减少计算量。(2)在提取声场特征频散曲线时,由于浅海声速剖面存在一个较大的跃层,破坏了部分声场的频散结构。在利用warping变换提取气枪声源信号的频散曲线时,舍掉因声速剖面跃变造成的频散结构被破坏的低模态频散曲线,提取较为准确的第三阶到第八阶简正波的频散曲线。(3)修正因接收水听器阵起伏引起的传播损失误差。
本文第一部分基于浅海声场简正波理论与理想波导的warping变换,导出含海底声学参数的代价函数,给出反演方法及流程图;第二部分介绍实验及数据处理情况,分别反演求得海底声速、密度,通过回归的方法得出海底衰减随频率的变化关系,将地声反演获得的声学参数分别代入频散曲线和传播损失公式进行数值模拟,由模拟与实测曲线拟合程度检验参数反演方法的有效性;第三部分为讨论与结论。
1 理论及反演方法
1.1 浅海简正波理论及warping变换[10]
假设浅海地声模型为半无限空间,声源和接收点在二维空间中的位置分别为(0,zs)、(r,zr),其中0、r和zs、zr分别为声源、接收点的水平位置和垂直深度。根据浅海简正波理论,接收点声场P可以表示为
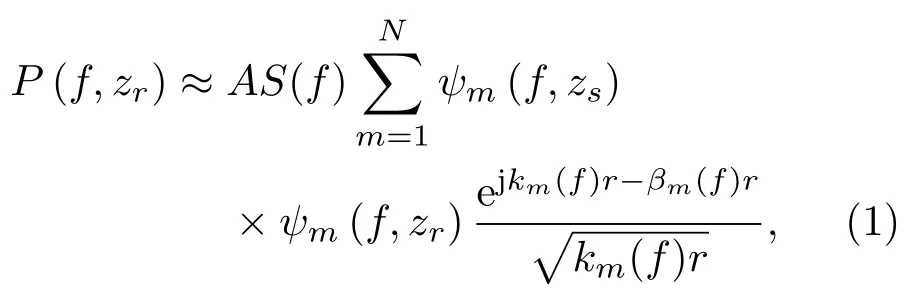
其中,N为传播的最大模式数,ψm为第m阶简正波的本征函数是第m阶简正波的水平波束,βm(f)是第m阶简正波的衰减系数,S(f)是声源的谱级。其中,ρ(zs)是声源所在深度水的密度。
由稳相法其可以表示为
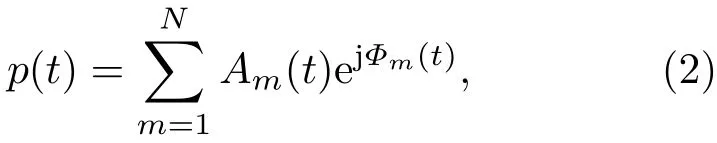
其中,Am(t)、Φm(t)是在t时刻m模态的幅值和相位。对于理想的波导环境其瞬时相位,

式(3)中,fcm为理想波导条件下第m阶简正波的截止频率,绝对硬海底情况下为

因为低频带声信号在浅海波导中呈现出频散效应,第m阶模态简正波的频散曲线满足

其中,tm为第m阶简正波到达的时间,vgm是第m阶简正波的群速度。对于既定的浅海波导,群速度vgm是一个常数,它由波导的环境参数决定,所以在获取到不同号简正波的群速度后,可以用它来反演海洋环境参数。
将式(3)中理想波导的瞬时相位带入式(2)中,得
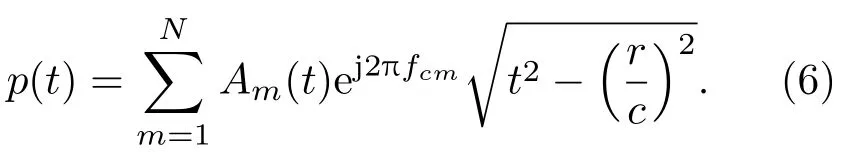
由式(6)知其相位随时间呈非线性关系,为消除相位的非线性,引入算子

其中,warping变换算子为

将式(8)代入式(6),则式(7)为

经过warping变换以后,信号的相位变成了时间t的线性函数,这里信号的幅值不太直观。现在,分别由式(6)与式(9)求得各自时间域上的能量,式(6)能量表示为
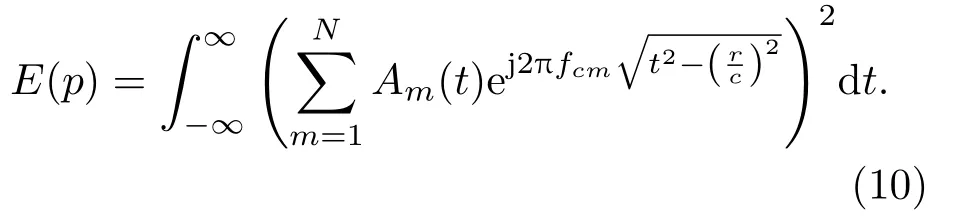
式(9)能量为
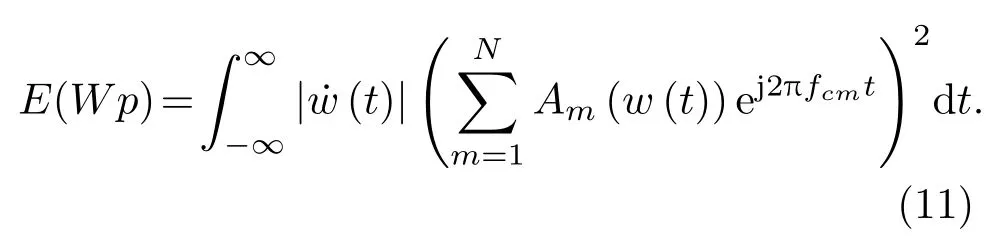
将式(8)变为
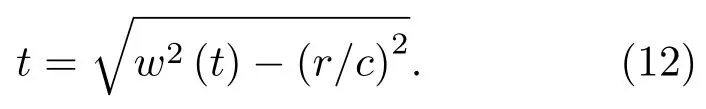
将式(12)代入式(11),可得
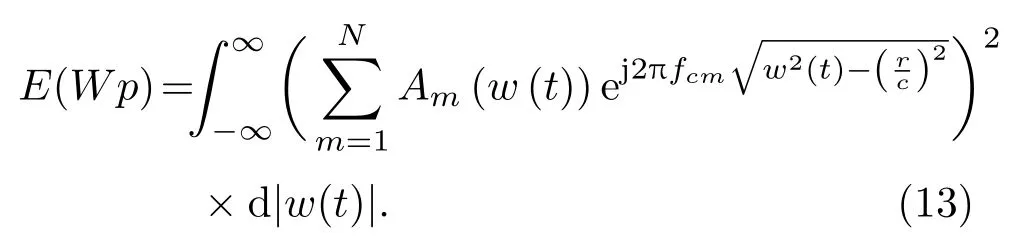
因为变换过程中满足能量守恒,所以式(10)与式(13)分别表示的E(p)、E(Wp)满足E(p)=E(Wp),即warping域的帕萨瓦尔定律。warping变换基于理想波导得出,但它适用于大部分海底反射类简正波情况[19]。
1.2 海底参数反演方法
由于海底不同的声学参数对声场测量值敏感性不同,可将海底声学参数分步反演。其中,海底声速对模态的频散曲线最为敏感,故利用频散曲线反演海底声速最为有效。而海底沉积层中的声速、密度均与孔隙率有着密切的关系,这里利用Hamilton经验公式中海底声速c和密度ρ的关系:
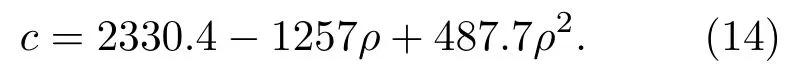
根据反演海区声速变化范围的先验知识,在合理的范围内对海底声速进行搜索获取海底密度,然后将其代入声场计算程序。代价函数为

这里,m代表简正波的阶数,f代表反演频点数,频带范围约为60∼300 Hz,(r/t)mf为按照式(5)计算所得第m阶简正波的群速度,Ω为待反演参数,反演过程中考虑了海深对频散曲线的影响。
声波在浅海传播过程中,波阵面的几何扩展、波导介质吸收以及边界散射均可引起声能量的损失。海表面近似为软边界,对声波造成的能量损耗较少。对于低频段,由于海底衰减远大于海水吸收产生的能量损失,故在传播损失表达式中略去海水吸收的影响,这样可直接利用传播损失拟合获取海底衰减。在获取海底声速与密度后,代价函数为

其中,d代表不同深度的传播损失值,TL为传播损失,TL测量、TL仿真分别为传播损失测量值和不同衰减系数下的仿真值,当式(16)取最小时,获得的衰减系数α为对应频率的衰减系数。
基于上述理论分析,可给出如图1所示的反演海底参数流程图。首先,对接收到的气枪声源数据进行预处理,选择距离合适的气枪声源进行短时傅里叶时频分析与warping变换,通过提取不同阶简正波的频散曲线来反演海底声速;然后,利用实验测量的传播损失拟合来获取海底衰减;通过选择多个距离的气枪声源及多个深度的传播损失使得反演结果更稳健,同时拟合的频散曲线与传播损失也是对反演结果有效性较好的验证。

图1 地声反演流程图Fig.1 The flow chart of geoacoustic inversion
2 实验与数据处理
2.1 实验情况
海试数据于2017年7月东中国海海域获得,实验船为“实验一号”,船在指定站位点将32元垂直阵布放到海中,阵元从上到下依次标记为1号∼32号,阵元间距为1.5 m,阵元处附有深度传感器,可记录阵随时间变化的阵元深度,1号阵元开始位于海深47.85 m处。布阵完毕后,测量海水声速剖面;阵元采集信号频率为17067 Hz;“实验一号”发射船沿着指定航线在一定距离上使用气枪声源发射信号,发射深度约为10 m,气枪的声源级频响曲线如图2所示;船在航行过程中同时记录航线的GPS及海深变化情况,实验期间约为一级海况。声速剖面见图3,表层声速约为1540 m/s,在海深60∼85 m为跃层,之后声速恒定于1518 m/s;实测海深环境如图4所示,大致在30 km的范围内海底较为平坦。

图2 气枪的声源级频响曲线Fig.2 The frequency response curve of source level of air gun

图3 声速剖面Fig.3 Sound speed profile

图4 实测海深情况Fig.4 Environment parameters of the experimental sea area
2.2 数据处理与参数反演
选择接收深度合适、水平距离在10 km∼20 km范围内的七个距离点的水听器阵接收数据。进行预处理后根据式(9)对信号进行warping变换。图5(a)和图5(b)分别为水听器阵水平距离13.87 km处接收到的信号及warping变换时域图。对其做短时傅里叶变换可得时频图(图6),由图6(a)可见其频散结构较为明显,图6(b)中某些频点处呈现一定宽度且稍微倾斜的亮条纹。其每一个条纹对应式(9)相位中的第m阶简正波截止频率fcm。按照理想波导条件,若海底为理想硬边界,fcm精确值可由式(4)得出:取测量海深约115 m,海水平均声速约1530 m/s,得出其前八阶简正波截止频率约为3.25 Hz、9.74 Hz、16.24 Hz、22.73 Hz、29.23 Hz、35.73 Hz、42.22 Hz、48.72 Hz。观察图6(b)可知实际浅海波导较为复杂:其中第一阶简正波受干扰较大且与第二阶简正波之间有明显干涉现象,高阶简正波呈现倾斜的宽条纹。这些现象主要由以下两点原因引起:海洋中低频段噪声较大,包括外来噪声及阵摆动的流噪声;warping变换基于理想波导得出,海水声速剖面和浅海波导对其影响较大,特别是本次实验海区的声速剖面存在一个较大的跃层,破坏了部分声场的频散结构。
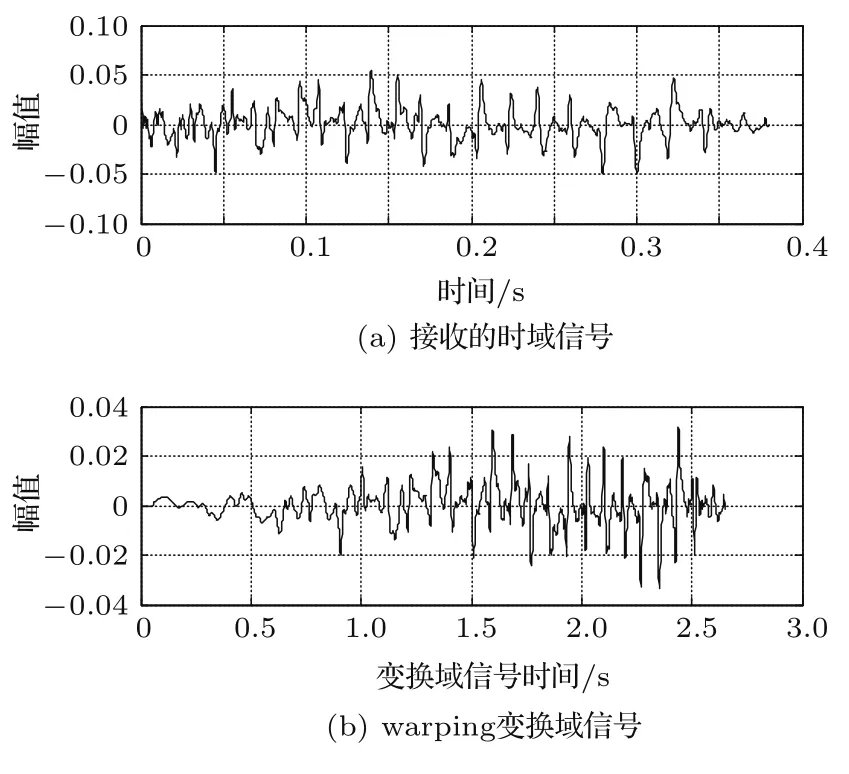
图5 接收的时域信号和warping变换域信号Fig.5 Original signal and warped signal
针对提取低模态频散曲线有较大误差的情况,在实际数据处理时,仅提取部分较为准确的频散曲线:首先对接收信号进行warping变换,从图6(b)所示的时频谱及频散曲线可看出各模态之间分离较为明显,再分别取第三阶至第八阶简正波各自频带内的极值,进行warping逆变换获得频散曲线,见图6(a)中白线。
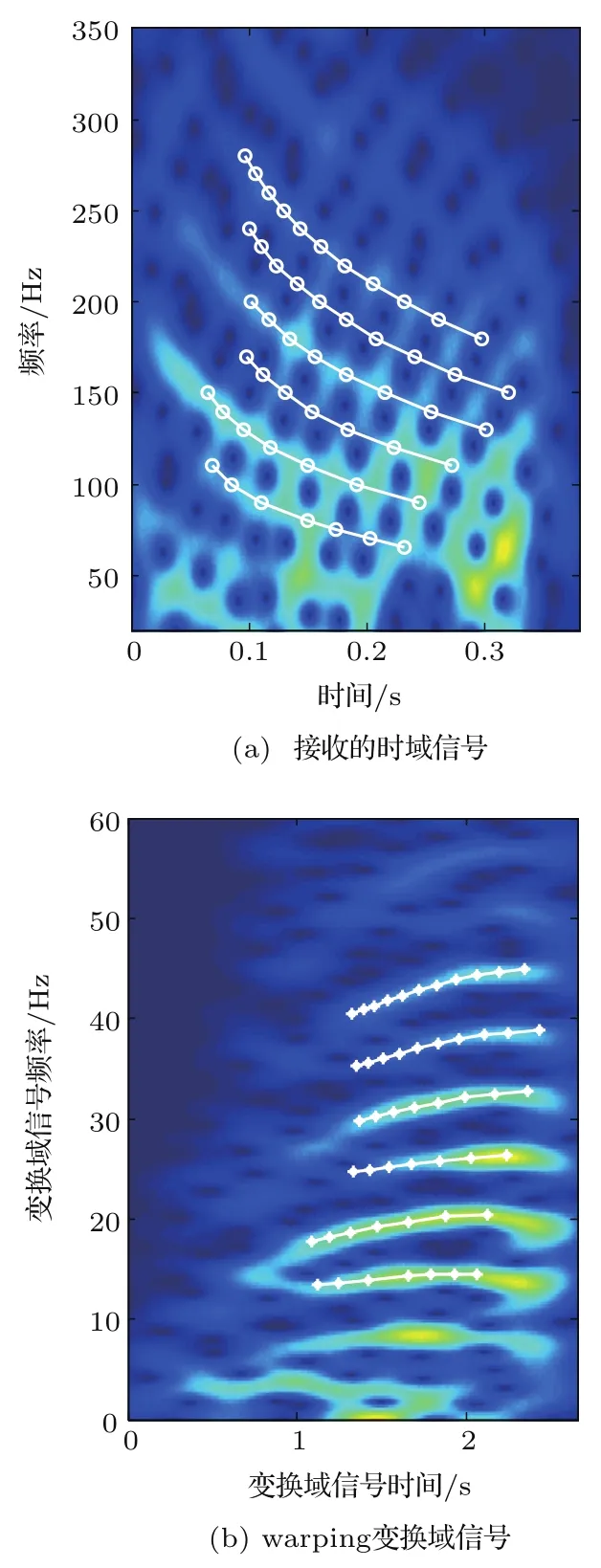
图6 接收的时域信号和warping变换域信号的时频谱及提取的频散曲线Fig.6 Spectrogram and the extracted dispersion curves of the original signal and warped signal
在获取第三阶至第八阶简正波的频散曲线后可进行地声参数反演。地声模型的选择是反演的基础,较为广泛使用的模型为水平均匀的半无限海底与沉积层加基底的双层海底模型。这两种模型能够较好地解决大部分的地声反演问题且模型简单,需要反演的参数较少。本次实验的海区地势较为平坦,故选取的海底地声模型为水平均匀的半无限海底,所需的反演地声模型参数包括海底声速、海底密度以及海底衰减系数。其中,海底声速对频散曲线最为敏感,海底衰减只影响各阶简正波的能量衰减,对频散结构几乎没有影响,故利用频散曲线反演海底声速和密度时,衰减系数可以设为任一合理值即可,在实际处理中取0.1 dB/波长。本文采用声场计算模型为Kraken,算法采用自适应模拟退火算法[20]。如图6(a)中,每一阶简正波频散曲线(白线)上的白色圆圈代表反演使用的频点数。
表1为七个不同距离数据的反演结果。图7给出反演参数及其均值,从图7中可以看出,不同距离点反演的海底声速较一致。将反演结果带入求得数值仿真的群速度,并与实验提取的群速度进行对比,结果见图8。其中黑线为数值计算的群速度,红色圆圈为实验提取的群速度。

表1 地声参数反演结果Table 1 The invert result of seabed parameters

图7 反演海底声速、密度及其均值Fig.7 The inversion result of the seabed sound speed,bottom density and their average values
式(1)中,βm(f)代表第m阶简正波的衰减系数,在低频段(1kHz以下),海水吸收相比于海底小几个数量级,其主要受海底衰减影响。获取单模态简正波较难,相比之下,利用传播损失直接拟合更为简单。实际海洋实验中,海流冲击等会引起接收阵姿势变化,需要根据深度传感器数据、水听器阵接收时间及气枪发射声信号时间,对不同距离的阵元进行深度修正,修正结果见图9。

图8 实验数据计算的群速度与反演结果数值仿真的群速度Fig.8 The contrast between numerical calculation in spectrum and extracted result of group velocity

图9 实验实测阵元深度及修正深度Fig.9 The measured depth of hydrophone and modified depth
在获得海底声速和密度的条件下,根据修正的传播损失来估计海底衰减系数。本次处理分别取修正传播损失上、中、下三个深度的数据进行拟合。所得衰减系数结果见表2。根据表2中海底衰减与频率的对应关系,利用回归分析方法对数据结果按照关系式进行了拟合,在80∼630 Hz频段范围内,拟合结果为α0=0.18,n=1.2,如图10(a)所示,图10(b)是频率用对数表示的情况。Stoll等[21]通过实验数据得出在10∼1000 Hz频率范围内,海底衰减随频率的变化呈非线性(1 图10 海底衰减拟合曲线及随频率的变化关系Fig.10 The fitting of seabed attenuation and it as a function of frequency 本文通过对七个距离点的气枪声源数据进行处理,首先提取第三阶简正波至第八阶简正频段覆盖60∼300 Hz的频散曲线,并结合海底声速与密度关系的Hamilton经验公式获取到对频散曲线敏感的海底声速与密度,频点包括80 Hz、100 Hz、160 Hz、200 Hz、250 Hz、315 Hz、400 Hz、500 Hz、630 Hz等涉及三个倍频程。传播损失修正与拟合,得到半无限海底的衰减。由此过程及结果得知: (1)气枪声源能够获取到频带更宽的频散曲线,可用于海底反演的有效数据比爆炸声源多,但要获取各阶简正波的截止频率处及附近的频点数据还有困难。 (2)为使得反演结果具有可靠性,利用不同距离的多个数据进行反演。同时,反演过程中要考虑复杂海洋环境对实验数据产生的影响,数据预处理阶段分别对低模态影响较大的频散曲线进行舍弃以及对传播损失进行修正。 表2 海底衰减系数Table 2 Seabed attenuation 图11 修正深度59.7 m处多个频率对应的传播损失实验值与反演参数计算理论值的对比Fig.11 The contrast between numerical calculation of transmission loss and extracted result from different frequency points at the modified depth of 59.7 meters (3)利用不同观测量对地声参数的敏感性不同,分步参数反演所得海底地声模型不仅能减少计算量,且能很好地应用于传播损失的预报。 (4)反演参数数值仿真的和实测的频散曲线间(见图8)、在各个频率点传播损失随距离变化曲线间(见图11)呈现了较高的吻合度,证明反演参数值是可信的,提出的反演方法是有效的。 致谢感谢中国科学院水声环境特性重点实验室的出海实验及“实验一号”海洋调查船的全体工作人员,他们为本文获取了宝贵的实验数据。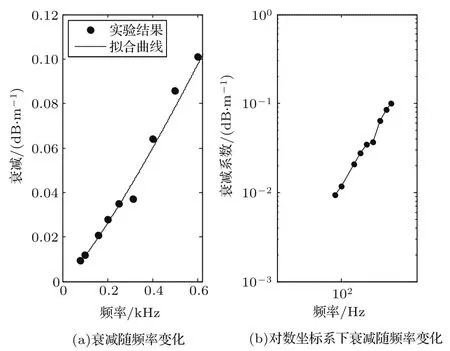
3 讨论与结论



