各向异性油藏水平井变流量压力动态响应计算方法

孟宪伟 刘洪杰 王佩文 郑建军 刘军 张浩

中海石油（中国）有限公司蓬勃作业公司

水平井作为一项高效开采技术以提高单井产能、提高储量动用程度、提高采收率等优势，在底水油藏、稠油油藏、裂缝性油藏、低渗透油藏、天然气藏等各种类型油气藏开发中得到广泛应用。国内外学者对水平井的压力动态分析和产能等关键技术都进行了深入的研究。针对水平井压力动态分析，目前有以点源函数理论为基础建立不同油藏类型下的水平井试井模型，此外还有通过建立拉氏空间无因次压力关系分析压力动态的方法。其中以点源函数理论建立试井模型研究最为广泛和深入。

1959年，Carslaw第1次将点源函数和Green函数引入热力传质学［1］。Gringarten于1973年对于点源函数方法进行了基于实数空间下的详细推导和说明，给出了用于不稳定压力分析的诸多实用的瞬时源函数，为建立水平井实空间渗流数学模型奠定了基础［2］。一些学者采用拉普拉斯变换和数值反演求解不同情况下的压力动态，如Ozkan于1991年依据拉氏变换提出一般情况下的拉氏空间中点源解的压力分布渗流数学模型，该通解考虑不同的井型、边界类型以及不同油藏类型的拉氏空间解析模型并提供相应的快速算法，对研究不稳定压力分析产生深远影响，但仍然没有很好地解决其计算方法问题［3］。Clonts、Goode、Daviau、lssaka等学者对水平井试井问题进行了充分的研究［4-7］。Ezulike从基本流动方程出发，建立了拉氏空间内水平井分段无因次线源函数解，最后通过stehfest数值反演进行求解，该方法解决了水平井在分采条件下，关掉贼层后相应水平段流量变化时的压力典型曲线，该试井模型假设在单分采水平段内的流量不变［8］。

国内学者对点源函数理论研究及水平井试井模型的研究始于上世纪90年代。孔祥言针对分支水平井各向异性气藏，导出气藏拟压力的瞬时点源解,利用瞬时源函数和Newman乘积原理，给出气藏中各种分支水平井的Green函数解析表达式，并给出了常用的基本源函数表，方便了点源函数理论应用［9］。廖新维用点源函数和格林函数法推导出拉普拉斯空间线源解。沿井筒平均流量解可得无限导流解,在拉普拉斯空间用叠加原理加上井筒储存和表皮效应的影响,再用数值反演方法得到含井储和表皮的真实空间解。通过参数组合得出考虑井筒储存和表皮因子的更具有实用价值的理论图版［10］。宋付权应用源函数理论研究了单一直线边界油藏水平井的压力动态，得到水平井应平行于单一直线边界布置的结论为实际的水平井布井提供理论依据［11］。王晓冬、刘慈群利用积分变换方法和源汇叠加原理建立了拉氏空间箱式封闭油藏中定产量水平井无因次压力分布式，分析了箱式油藏水平井压力动态分析，提供了实用可靠的计算方法；用积分变换、汇源叠加方法求得其数学模型的Laplace变换解式并建立了快速、实用的应用方法，通过典型曲线计算方法、调参分析方便了水平井不稳定试井资料的分析与解释［12-13］。汪志明根据Newman乘积原理和叠加原理，利用瞬时点源方法推导出了多分支水平井在箱形有限地层中的压力分布通式，研究了水平井分支数、渗透率平面非均质性以及水平井水平段长度与水平井产量的关系［14］。段永刚采用点源函数的方法通过对水平井在无限大油藏、一条断层、直角断层以及封闭矩形等条件下的压力动态，在数值反演计算中同时考虑表皮系数和井筒存储对压力动态的影响,分析了水平井压力动态［15］。李成勇利用点源函数的思想建立了边水气藏渗流常产量下的数学模型，利用stehfest反演算法求解该模型；并且利用点源函数的思想,求解了各向异性无限大地层水平井在拉氏空间中的无因次压力响应，在拉氏空间中,讨论了无穷累加项中累加次数的取值问题,简化了其理论压力动态响应曲线的计算过程［16］。李树松利用点源函数为基础建立了水平井和多分支井的不稳定渗流模型，同时在拉氏空间进行了求解［17］。刘振宇以点源函数和格林函数的思想为基础求解出一条直线边界油藏中的水平井压力响应模型，对流动阶段及边界影响进行分析认为边界对水平井压力的影响主要表现在边界的类型及距离上［18］。周密采用Green函数和叠加原理方法求解了在Laplace空间下水平井井底压力计算公式，并利用改进的Stehfest算法反演得到实空间的井底压力，分析了水平方向钻遇断层后压力变化特征［19］。杨志刚运用Lord Kelvin点源修正解，考虑启动压力梯度影响，结合杜哈美原理和泊松公式求解了低渗透油藏水平井的点源解，通过无因次压力导双对数图版分析了低渗气藏水平井渗流特征及其影响因素［20］。方思冬利用Green函数和拉普拉斯变换建立裂缝流动的一维单元，建立有限导流裂缝井底压力的求解方法分析了多裂缝水平井在不同流动形态下的压降变化和对产能影响［21］。王家航应用点源函数理论和边界元思想，建立一种可用于非均质油藏多段压裂水平井非稳态压力分析的半解析模型，对储容比、窜流因数、裂缝导流能力、长度及各裂缝泄流面积的影响进行讨论［22］。

对于各向异性油藏的研究，刘月田利用坐标变换，将各向异性油藏转化为各向同性油藏进行求解［23］；何应付将各向异性坐标变换应用到边界元方法中求解封闭地层各向异性油藏压力动态［24］。由于油藏各向异性是在自然条件下随机形成，影响因素较多，利用试井分析油藏系统本身就是黑箱问题，考虑各向异性的角度是从笛卡尔坐标系下直接建立各向异性油藏模型，在计算时要求各向异性物性参数在求解时满足一定约束条件以符合实际生产动态。最后在求解结果的基础上对模型后续动态进行预测，达到可现场应用目的。

综上所述，对于空间连续点源情形的压力分布数学模型的研究，大部分学者主要从实数空间和拉氏空间2个方向建立数学模型。其中在实数空间中建立点源函数的数学模型复杂度高，在复杂地质油藏条件下由于模型复杂程度高在实际应用时受到限制，为满足实际应用条件，通常需要设立诸多限制条件，如对边界形状、油藏压力和产量等条件进行限制；而在拉氏空间建立的数学模型虽然可建立较复杂模型，如解决近井存在有限或无限导流能力的情况、井储和表皮情况、水平井过断层情况等复杂条件；但涉及的反演计算复杂，由于目前工程上常用的数值反演算法有基于函数概率密度的Stehfest反演算法和基于Fourier变换的Crump反演算法。Stehfest算法稳定性和精度不如Crump算法，但Crump算法的计算速度较慢阻碍了在实际中的应用。另外，通过大量文献调研，国内外学者对于水平井试井数学模型的建立多数定流量条件下的试井压力分析，对变流量情况下的压力分析较少。

通过引入信号与系统分析理论中卷积和矩阵概念，结合点源函数理论建立水平井变流量压力动态响应离散模型。最后利用最优化方法对该模型直接计算，求解模型最优解，避免了反演计算。计算过程和结果精简可靠。克服了缺少精密压力数据条件下不稳定试井分析方法的应用，克服了常规模型中流量不变的假设，解决了流量变化条件下的压力响应问题。文章中推导的试井解释模型适用于解决有界断块内封闭边界，水平和垂直方向各向异性油藏中水平井在变流量条件下的压力响应问题。在不同边界形状和条件下，对点源函数进行扩展，可适用于定压边界和混合边界的模型应用。扩展后可适用于对应地质油藏条件下的试井模型建立和计算。

1 各向异性油藏变流量水平井试井模型

在变流量条件下，试井数学模型建立的理论依据为格林函数和Newman乘积原理，同时结合系统理论中单位冲击响应函数和系统输入输出关系，对水平井流量变化时的压力响应进行分析和计算。利用格林函数理论构造点源函数和Newman乘积方法建立矩形断块内各向异性油藏水平井的点源函数，该函数在模型中表征了系统的单位冲击响应。变流量条件时表征为系统输入信号的变化，水平井跟端压力响应即为系统的输出。该系统模型在实域空间的解析式即为杜哈美原理导出的褶积表示式。

从基于格林函数的点源函数理论出发，将模型分解成实空间3个方向的瞬时点源解，结合Newman乘积原理构造水平井瞬时源函数解。最后建立基于变流量条件下瞬时点源解的连续系统卷积公式。并根据离散系统的卷积和关系，将连续系统卷积公式变换成为基于各个测试点的卷积和矩阵关系式，最后利用该卷积和矩阵关系进行模型的计算。

1.1 各向异性油藏基本控制方程

考虑到矿场实际条件下，可获取的数据质量情况，地质油藏状况，以及井筒状况，同时为简化计算，降低计算的复杂度。针对模型建立如下假设条件：将水平井假设为封闭断块内的水平直线源，因此模型不考虑水平井井筒半径的影响；有界断块内各点水平渗透率和垂向渗透率分布一致，模型假设为均质各向异性油藏；单相弱可压缩流体，流体黏度均匀分布；水平井井筒流量随而时间变化。

在不考虑井筒储集效应和表皮系数的条件下，考虑水平方向和垂直方向的各向异性，利用连续性方程和达西定律建立各向异性油藏控制方程为

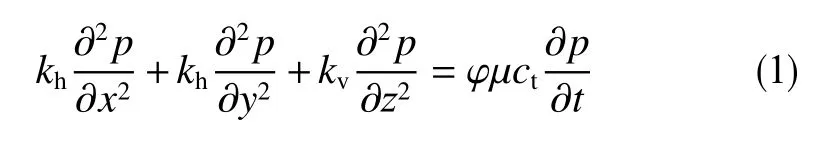
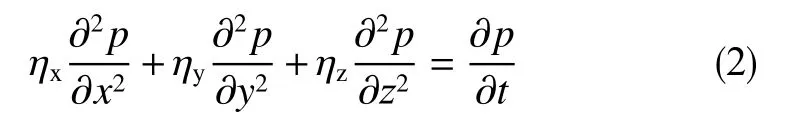
由于求解该扩散方程的水平井变流量模型涉及带时间变量的复杂边界条件，直接求解困难。而利用Green函数理论建立变流量条件下点源函数模型将边界条件影响体现在不同的瞬时点源函数。

1.2 各向异性油藏水平井点源函数构成

由于控制方程满足线性叠加原理，其解也满足叠加原理，利用点源函数思想解决水平井不稳定渗流问题，将各种类型的边界条件体现在点源函数的源函数上，结合卷积原理解决变流量问题；对于空间连续点源情形的压力分布Gringarten利用了热力学方面研究成果，采取Newman乘积方法在实域中给出变流量解，该压力解为褶积形式为

式中，S(x,y,z,t-τ)为模型源函数，cm-2；q(τ)为模型中源的单位冲击强度，cm3/(s·cm)。

设地层顶底面为封闭不渗透地层，地层厚度h/cm，水平井位于封闭断块内且平行于顶底面，平行于水平井井筒方向的断块边界水平距离xe/cm，垂直于井筒方向断块边界水平距离ye/cm。建立坐标系如图1所示，水平井水平段长度为L/cm，水平井中点坐标为(xw，yw，zw)。水平渗透率为kh，垂直渗透率为kv。

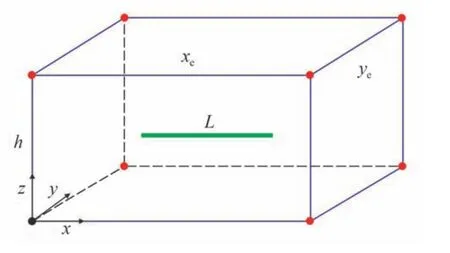
图1 边界为封闭断块内一口水平井油藏模型Fig.1 Reservoir model of horizontal well in a closed fault block

对于顶底面封闭不渗透层、有界封闭断层内一口水平井油藏系统来说可分解成为x方向为条带形封闭边界内宽度为L的条带源、y和z方向为条带形封闭边界内直线源，断块内水平井瞬时源函数为3个方向瞬时源函数乘积。如图2所示为3个方向的边界条件示意图。

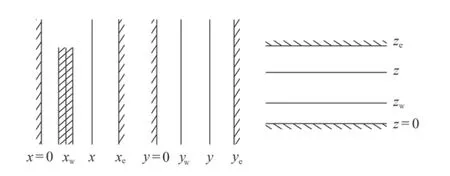
图2 封闭断块内平行于顶底面水平井分解为源函数模型Fig.2 Decomposition of horizontal well parallel to the top and bottom surface in a closed fault block into the source function model

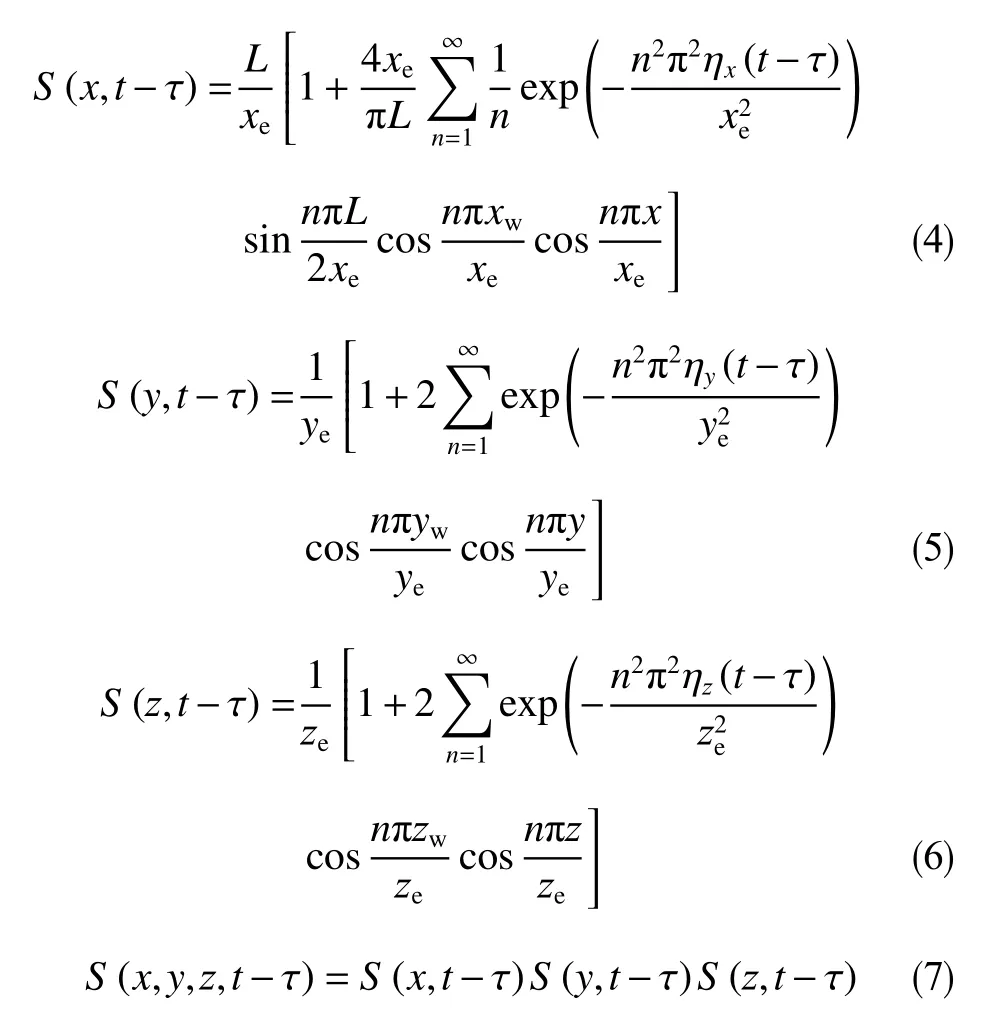
上述3个源函数反映了3个方向上对应的边界条件下的表达式，根据Newman乘积原理整体模型的源函数可表示为3个方向的源函数乘积，该模型同时满足整体的边界条件。

1.3 变流量下水平井压力动态响应关系式建立

以水平井跟部位为压力测试基准点，可得到水平井跟部井壁流压变化关系式，由式(3)得到变流量下水平井跟部流动压力动态响应关系式为

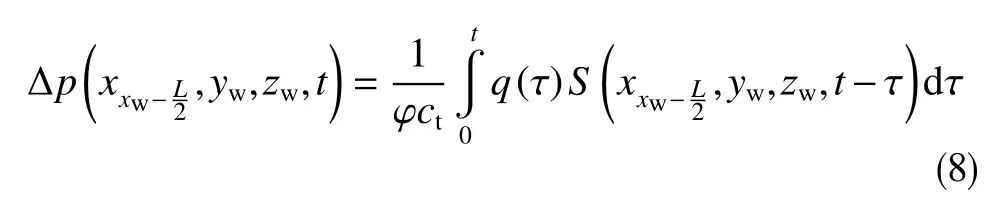
对于封闭边界条件下，式(8)中点源函数在跟端的表达式为

式(8)中q(τ)的数学物理意义为输入该模型的单位冲击信号，在变流量情况时表征为单位空间尺度下的流量随时间变化的函数。针对所建立的模型为封闭断块内各向异性油藏水平井可表示为q(τ)=BQ(τ)/L。而源函数即为信号与系统理论中的单位冲击响应函数，两者的卷积为系统的输出信号，此处即为压力响应。式(9)为封闭边界条件下点源函数在跟端的表达式。同理，依据文献[2]提供的基本源函数，基于上述相同的假设条件，可建立定压边界和混合边界条件下断块内水平井跟端点源函数表达式如下 (10)、(11)所示。

在上下顶底面封闭边界、平面定压边界条件下，水平井跟端压力响应点源函数(单位冲击响应函数)表达式为

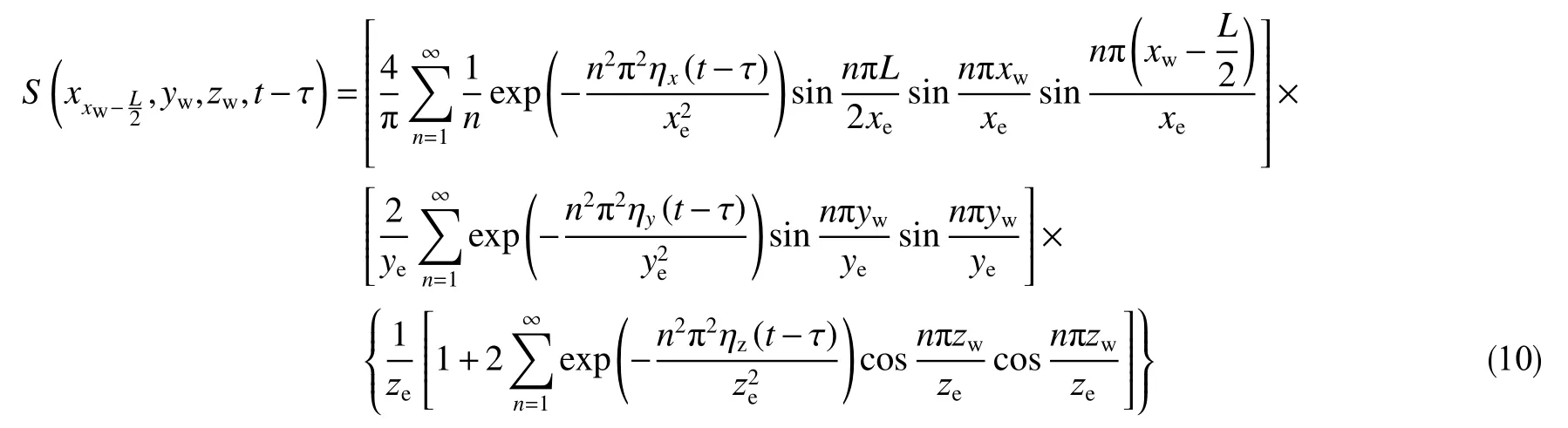
在上下顶底面封闭边界、平面混合边界条件下，点源函数表达式为

在得到不同边界条件下的点源函数后，根据实际情况可将对应点源函数带入各向异性油藏水平井井底流压动态响应关系式(8)中进行计算。由于响应关系式为连续系统的表示形式，为了使该实数连续空间表达式具有可应用价值，将连续系统的褶积形式写成等价的离散系统卷积和形式为

为简化公式对式(12)进行简化，令

则式(12)简写成为式(15)为

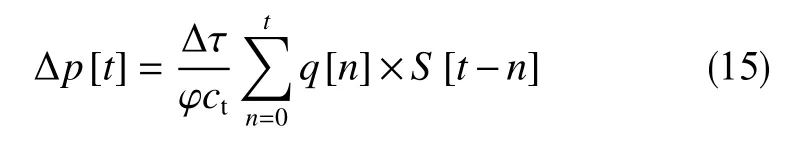
可以在每个测试点n=0,1,2,···,t，依据式 (15)进行展开后得到矩阵形式为

上述(16)式中Δτ取决于测试数据密度，对于每日测试数据可取Δτ=24 h。由于流量历史q[n]和压力历史Δp[n]已知，利用文献[25]中的计算思路和最优化算法求得该模型参数的最优解，编制计算机最优化程序实现计算结果。

2 矿场计算实例

由于上述卷积和形式的关系式反映了水平井跟端压力在变流量时动态压力响应，实际测试数据密度决定了模型的输入和输出数据质量，也决定了模型可认识程度。该井实例测试数据来源于混合边界断块中水平井日产数据，流压测试数据为日度数据。

X井为渤海区域某有界封闭边界和定压边界构成的混合边界断块内1口水平井，该井初期流量和压力变化实测数据见表1。从该井实测流量数据可知，该水平井流量变化较大，常规定产量模型不适用。为了利用动态监测中的日频度数据进行不稳定试井压力解释和分析，应用前面推导的基于源函数卷积和矩阵关系式模型进行模型拟合和计算。

基于油田矿场X井附近断层信息和该井附近压力支持的实际情况，建立该井静态模型，该模型中断层边界及水平井位置参数详细信息见表2。

由于3个方向源函数的计算都涉及到无穷级数项，在实际应用中，级数项个数n的取值会影响计算精度。为了在不影响计算精度的条件下减少不必要重复计算，应用本模型中源函数，对不同数目级数项下的源函数计算结果进行对比，如图3所示。

图3显示了不同级数项目个数的计算结果对比，在级数项个数n≤5时，源函数计算结果差别较大；而在级数项个数取值n＞5时，源函数计算结果差别较小。实际应用中建议级数项个数取值大于5，计算结果可以满足准确性和精度的要求。

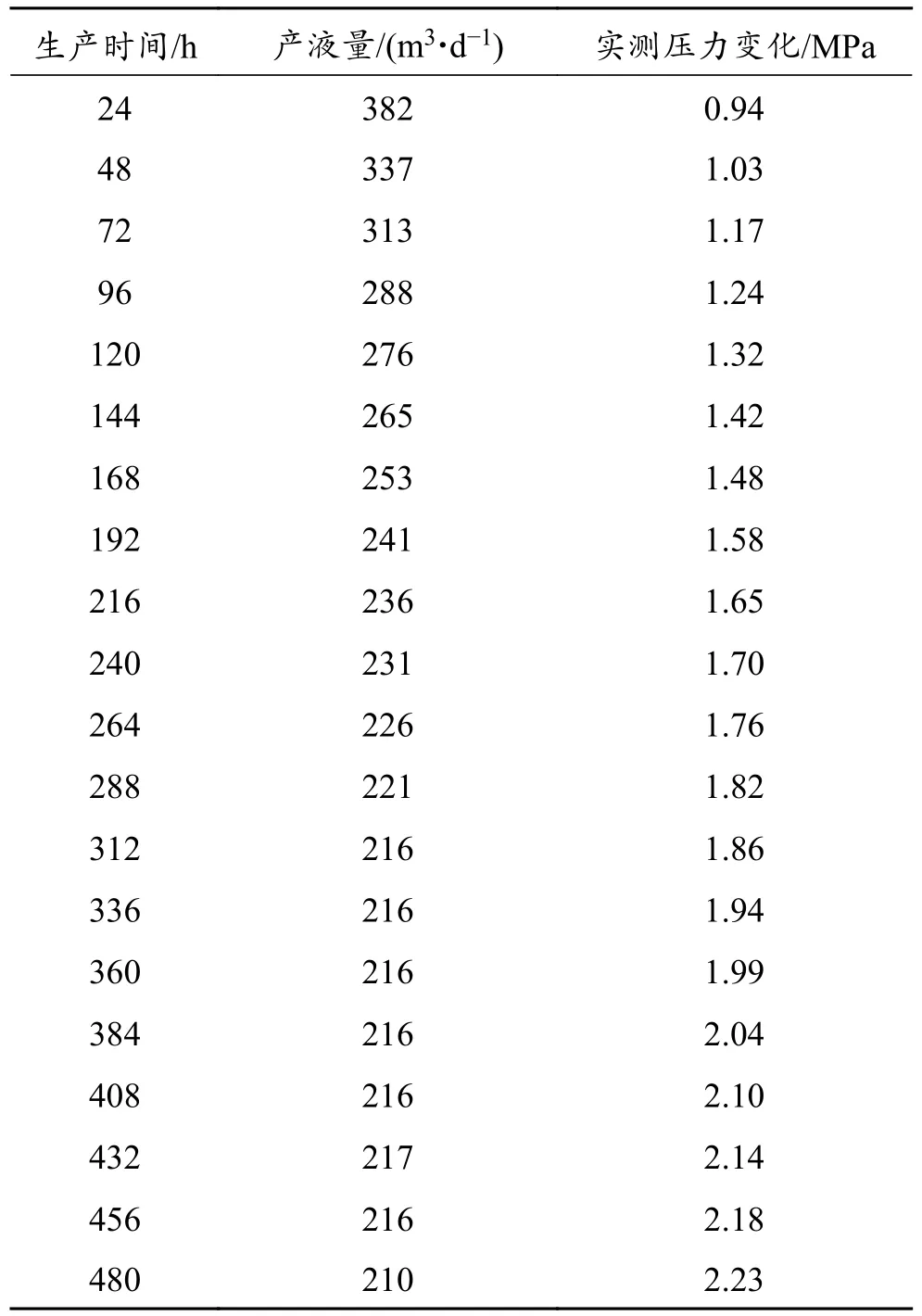
表1 X 井实测流量和压力动态响应Table 1 Flow rate and pressure behavior response measured in Well X

表2 X 井静态模型参数Table 2 Static model parameters of Well X

利用初期测试流量和压差数据，结合上述卷积和矩阵乘积得到p[n]*，设置目标函数最小化为利用初始值计算模型的压力响应。利用优化方法求解目标函数极小值，达到优化模型参数符合该井实际测试数据，编制计算机最优化程序算法，计算后得到模型的压差。如图4所示，可知模型和实测的压力响应拟合结果吻合程度较高。模型计算结果与实际测试数据对比其相对误差情况统计见表3，相对误差平均在3.1%左右。从实际应用表明，该模型所用方法具有较高的可靠性，具有应用价值。

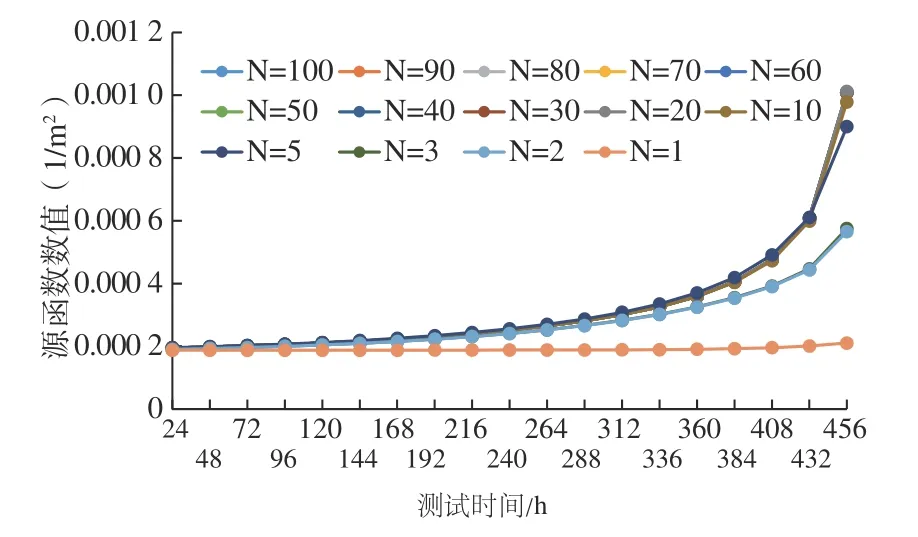
图3 级数项不同取值个数下源函数计算结果对比Fig.3 Calculation results of source function at different numbers of series terms

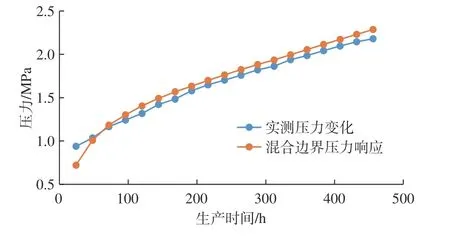
图4 各向异性混合边界油藏水平井变流量实测与模型压力对比Fig.4 Comparison between the calculated pressure and measured value of horizontal well at variable flow rate in anisotropic reservoirs with combined boundaries

表3 实测压力变化与模型压力变化相对误差统计Table 3 Relative errors between well test pressure change and model pressure change

最优化方法求解得到模型的决策参数结果见表4。由于该模型和求得的对应参数符合该井生产初期动态，后续可综合利用该模型的各项参数，对模型后续的动态表现进行预测。参数预测后续模型结果和实际生产数据对比如图5所示，预测结果与实际生产数据吻合程度较高。

表4 模型参数解释结果汇总Table 4 Summary of interpretation results of model parameters

图5 基于模型参数预测定流量下实测压力与模型压力响应对比Fig.5 Comparison between the measured pressure at constant flow rate and the modeled pressure response result

上述计算实例为混合边界条件下的变流量压力响应结果，通过历史动态数据拟合得出模型参数后，对模型后续动态进行预测，预测结果和实测数据吻合程度高，模型具有实际应用价值。利用封闭边界和定压边界下的点源函数，计算在相同的输入(流量变化史)、相同的模型参数下，得到不同的边界情况下该水平井压力动态响应结果，如图6所示。可以看出，模型在相同的流量变化条件和相同的模型参数条件下，实测压力数据与混合边界模型压力拟合程度较高，而封闭边界和定压边界模型在初期吻合程度较好，随着压力传递到边界后，后续的压力动态响应出现了明显的差异。说明了不同边界条件下，该井在相同的输入(流量变化史)时，不同边界模型初期的压力响应基本一致。为了后续能够预测该井动态，本计算实例采用混合边界模型更符合生产实际。

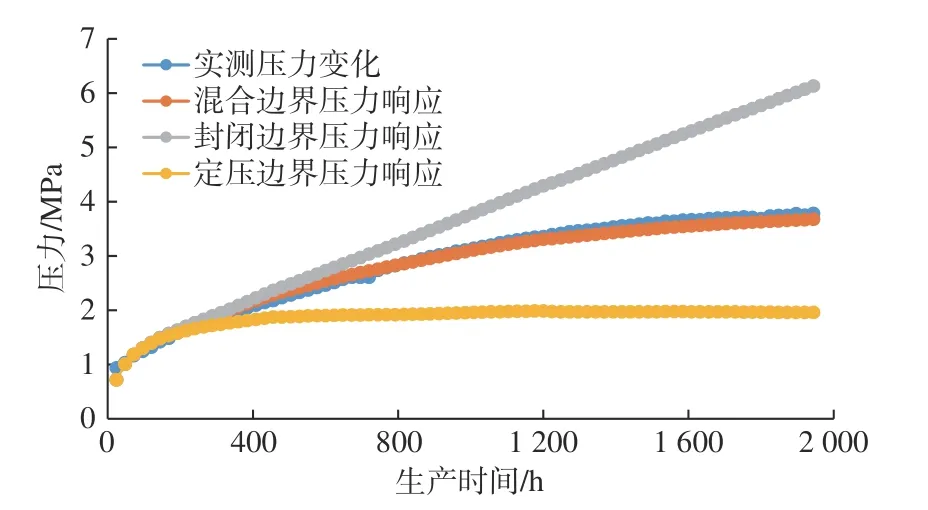
图6 不同边界条件水平井实测压力与模型压力响应结果对比Fig.6 Comparison between the measured pressure of horizontal well under different boundary conditions and the modeled pressure response result

3 结论

(1)利用点源函数理论和Newman乘积原理建立的各向异性油藏水平井在不同边界条件下的变流量压力动态响应卷积关系式，该模型适用于定压边界、封闭边界、混合边界条件下的不稳定压力分析。通过变换得到的矩阵关系式可利用计算的数据适用范围广，对数据频度要求低；计算结果可反求出油藏参数，该方法建立的模型反映出各向油藏水平井实际动态情况。

(2)模型实际计算过程中，水平井点源函数的级数项取值应大于5，以满足模型计算准确性和精度要求。利用最优化方法快速拟合了历史数据并求得了模型参数，实例应用表明对单井模型后续预测准确性较高，对油田开发评价和后续实际生产具有较高的实用价值。

符号说明

B为流体的体积系数；ct为综合压缩系数，atm-1；h为地层厚度，cm；kh为地层水平渗透率，μm2；kv为地层垂直渗透率，μm2；L为水平井水平段长度，cm；Δp为水平井跟端压力变化差值，atm(一个标准大气压)；q为水平段内单位长度井底流量，cm3/(s·cm)；Q为水平井井口流量，cm3/s；t为生产时间，s；ηx,y为地层水平导压系数，cm2/s；ηz为地层垂直导压系数，cm2/s；μ为流体黏度，mPa·s；φ为地层孔隙度。