沉井下沉侧壁摩阻力离心模型试验研究

张 凯，马建林，周和祥，罗朝洋，褚晶磊

(西南交通大学 土木工程学院，四川 成都 610031)

沉井[1-3]以其整体性强、刚性好、承载力高、施工方便等特点广泛应用于各类大跨度桥梁基础。对于超深大沉井的设计与施工，其核心问题之一是如何准确可靠地计算沉井下沉系数与稳定系数以保证下沉过程的安全稳定。而如何确定沉井侧壁摩阻力的大小及分布规律，并在此基础之上建立一个相应的计算模型是确定上述参数的关键。现行规范[4]对于深大沉井侧壁摩阻力的计算方法是依据大直径桩的下沉机理分析或针对中小沉井得出。虽然简单易行，但与现场实测结果[5]存在很大差异。在现场试验与室内试验方面，国内外学者均做了相关研究。陈晓平等[6]以海口某大桥沉井现场资料分析沉井下沉机理和受力特征，得出不同下沉深度下侧壁摩阻力的分布规律及计算模型。王建等[7]研制了直接测量沉井侧壁摩阻力的微型摩阻力仪器，并以此获得了侧壁摩阻力随下沉深度的发展曲线，对其发展趋势进行了理论分析。

现场监测试验存在数据波动性较大，数据量有限等问题；而针对沉井侧壁摩阻力的室内试验开展得较少，并且试验结果均在1g重力场条件下获得。离心模型试验借助离心力场模拟重力场，克服了重力场模型试验不能模拟原型重力场的缺陷，使模型具有与原型相似的边界条件和受力状态，可对沉井下沉过程中侧壁摩阻力大小及分布研究提供很好的支持。

本文依托沪通长江大桥29#墩沉井基础，开展室内离心模型试验，研究超深大沉井下沉过程中侧壁摩阻力的大小及其分布特性，并在此基础上提出可靠、合理的沉井侧壁摩阻力的计算模型，试验结果可为类似的工程提供参考。

1 工程概况

沪通长江大桥[8-9]位于江阴长江公路大桥下游约45 km处，是沪通铁路的控制性工程。主航道采用双塔五跨布置，跨度为(168+462+1092+462+168)m。桥梁主跨位于28#墩和29#墩之间，主跨长 1 092 m，设计为4线6车道公铁两用斜拉桥。

沪通铁路为双线Ⅰ级铁路，设计时速为200 km/h，公路为双向6车道高速公路。为满足桥梁结构承载力、沉降、防冲刷等要求，29#墩沉井基础设计为倒圆角的矩形沉井基础，平面尺寸为86.9 m×58.7 m。为方便吸泥下沉，平面布置为24个倒圆角矩形井孔，竖向由下部56 m的钢沉井和上部59 m的混凝土沉井组成。29#墩沉井基础结构见图1。

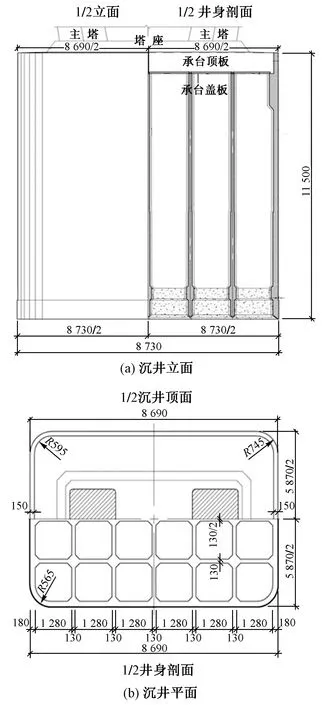
图1 29#墩沉井基础结构(单位：cm)

2 离心模型试验方案

2.1 试验设备与装置

2.1.1 土工离心机

试验采用西南交通大学数据自动化采集系统的TLJ-2型土工离心机，其最大加速度为200g，有效半径为2.7 m。

2.1.2 试验用模型箱

试验选用尺寸相对较大的自制模型箱，以减小尺寸效应的干扰进而提高数据的准确性。试验用模型箱内缘尺寸：长 800 mm、宽700 mm、高700 mm，重心高度302.2 mm。

试验模型箱底板与3个侧面板材质为钢板，正面采用有机玻璃，便于观察模型箱内的试验情况。在模型箱顶部相应位置按照设计依次钻孔，用于模型箱吊装以及与加载装置的连接。

试验模型处于水下环境，为保证模型箱的密封性，在模型箱内各接缝处涂抹一定厚度的玻璃胶。

2.1.3 试验用土的制备及其物理力学特性

选用粉质砂土作为试验用土，平均粒径为0.3 mm。在离心模型试验中，由于模型与材料缩尺的不一致，往往存在粒径效应[10-11]。本次试验沉井侧壁模型的宽度与试验用砂平均粒径之比为67，可忽略粒径效应对试验结果的影响。

试验中将砂土分层摊铺并利用室内轻型压实仪进行多遍夯实，直至到达设计高度。试验土样全部填筑完成后，通过模型箱中预先埋设的注水管缓慢从模型箱底部向上注水，当注水高度高于土面1 cm后停止注水，静置24 h，以保证土样的均一性。试验土样为粉质砂土，基本参数为：黏聚力0，内摩擦角36.2°，天然孔隙比0.73，干密度1.56 g/cm3，饱和密度1.984 g/cm3,土颗粒密度2.7 g/cm3。

2.1.4 沉井侧壁模型

沉井侧壁模型材质选用钢板，由上至下以中心线为对称轴依次布置2排土压力盒以保证试验数据的准确性与稳定性。沉井侧壁模型如图2所示。

图2 沉井侧壁模型示意(单位：cm)

2.1.5 试验元器件

试验选用江苏溧阳科源仪器厂研发的BW箔式微型土压力盒量测沉井侧壁外侧土压力大小；选用YWC型应变式位移传感器量测沉井侧壁的下沉距离。

2.2 试验过程

2.2.1 试验安排

通过离心模型试验[12-15]模拟沉井连续动态吸泥下沉的过程极为困难，因此试验选取沉井下沉过程中几个特定的时间点阶段性地分析其动态下沉过程。尽管存在一定的误差，但大大提高了试验的可操作性。

试验共分为4组，埋深分别为10，20，30，40 cm，离心加速度设定为90g，加载前保证沉井内侧土面与刃脚踏面相平。离心模型试验安排见表1。

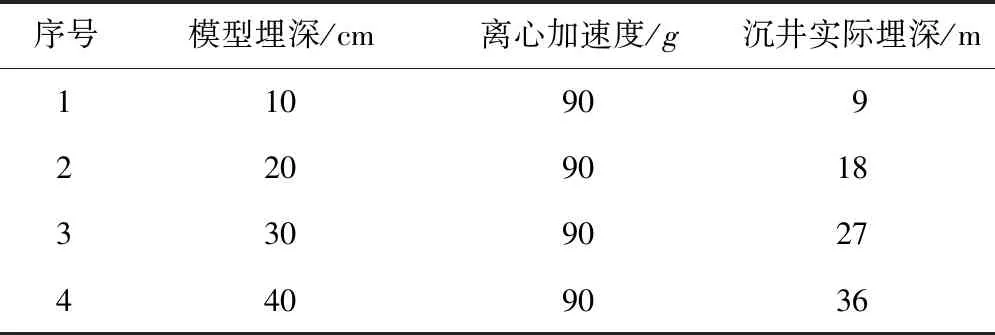
表1 离心模型试验安排

2.2.2 试验加载

采用自行研制的加载装置对沉井侧壁施加竖向荷载，通过操作系统控制加载装置缓慢匀速下降并通过加载装置与沉井侧壁上的连接装置带动沉井缓慢匀速下沉。当下沉距离达到2～3 cm后，停止加载。试验布置如图3所示。

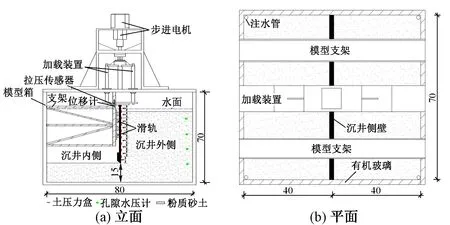
图3 试验布置示意(单位：cm)

3 试验结果分析

3.1 沉井侧壁摩阻力分析

根据上述试验条件，得到不同埋深情况下沉井侧壁有效土压力、摩阻力的大小及分布，见图4。

图4 不同埋深下沉井侧壁土压力、摩阻力分布曲线

不同埋深下沉井侧壁土压力分布曲线见图4(a)。由图4(a)可知：沉井侧壁有效土压力介于静止土压力与被动土压力之间，当入土深度较小时，侧壁有效土压力更接近于被动土压力。随着下沉深度的增加，沉井侧壁土压力逐渐增大，在入土深度达到2/3倍沉井埋深时，有效土压力达到最大值，随后由于沉井下沉使刃脚外侧土体有向内的趋势，在沉井外侧某一范围内形成压力松弛区造成侧壁有效土压力减小，且在靠近刃脚附近其减小幅度更大，数值偏向于静止土压力。

沉井侧壁摩阻力

fs=σatanφ

(1)

通过离心模型试验结果计算得到的σa和已知摩擦因数值0.47，由式(1)计算得到沉井在下沉过程中的侧壁摩阻力的大小，不同埋深下沉井侧壁摩阻力分布见图4(b)。由图4(b)可知：不同埋深下沉井侧壁摩阻力整体呈现上下小中间大的分布形式。当下沉深度较小时，沉井侧壁摩阻力与入土深度基本呈线性关系，且埋深增加时其线性增加部分比例逐渐降低。当下沉深度增加时，侧壁摩阻力随入土深度的增加先增大后减小。不同埋深下相应的摩阻力极值在一定的下沉深度内随着下沉深度的增加而增大，且发生的部位逐渐下移。

3.2 沉井侧壁摩阻力计算模型

根据离心模型试验结果，沉井侧壁摩阻力呈现上下小中间大的分布形态，考虑几种不同的数学模型进行结果拟合[16]，从而确定一种合适的计算模型。

3.2.1 抛物线形

根据离心模型试验结果，选取抛物线形函数进行拟合。拟合公式为

f=C+B1h+B2h2

(2)

式中：f为沉井侧壁摩阻力，kPa;h为沉井入土深度，m;C,B1，B2为拟合参数。

不同埋深下沉井侧壁摩阻力抛物线拟合曲线见图5，拟合参数见表2。

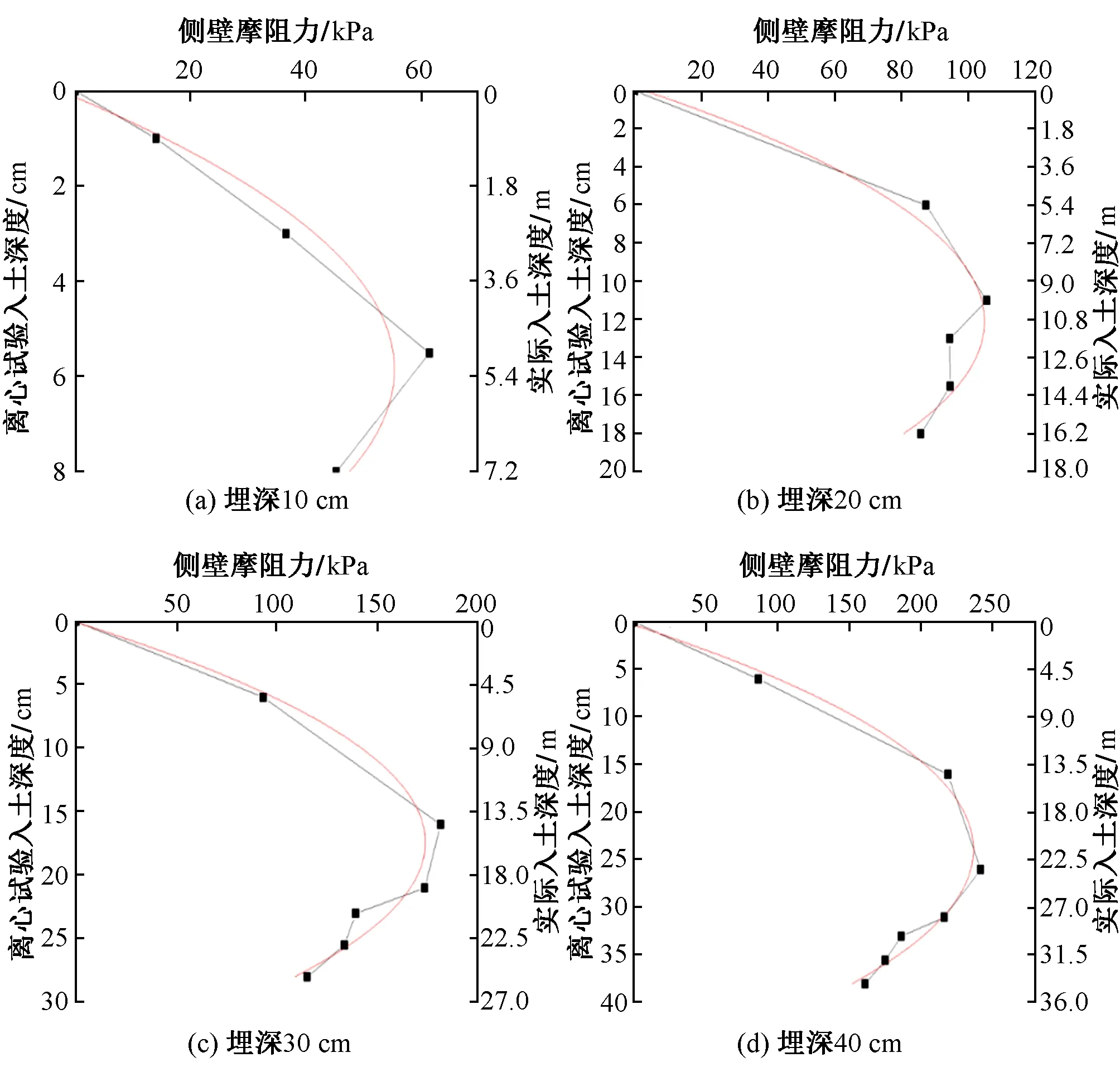
图5 不同埋深下沉井侧壁摩阻力抛物线拟合曲线

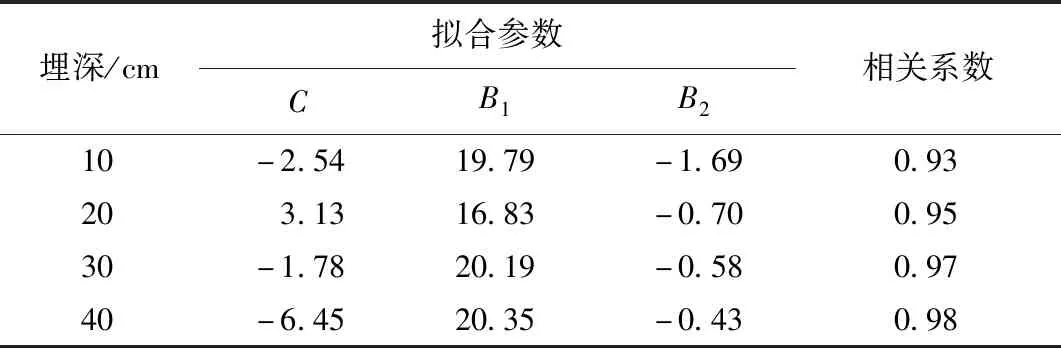
表2 抛物线形拟合参数

由图5及表2可知：在一定的入土深度范围内，采用二次函数曲线对不同埋深下沉井侧壁摩阻力的分布进行拟合，其相关系数较高，可以很好地反映侧壁摩阻力的大小及分布。但其拟合参数C，B1，B2规律性不强，且与土体性质、埋深等参数之间的关系无法较准确地确定，使其不便于工程应用。

3.2.2 分段函数包络线

考虑工程中的应用方便，采用分段函数包络线的形式拟合。拟合公式为

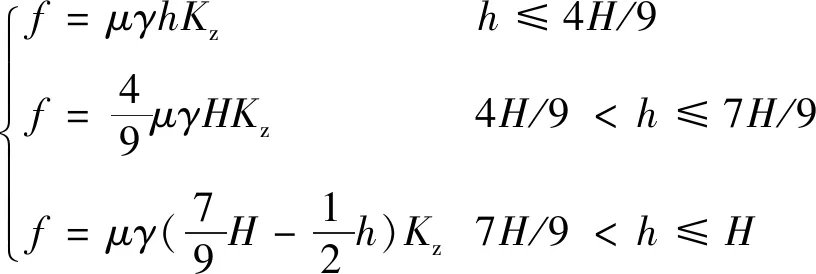
(3)

式中：μ为沉井侧壁与土体之间的摩擦因数；γ为土体的有效重度，kN/m3；H为总的入土深度,m；Kz为增大土压力系数，介于K0与Kp之间(K0为静止土压力系数，Kp为被动土压力系数)，考虑土体性质等因素的影响，本次试验中取0.85Kp。

不同埋深下沉井侧壁摩阻力分段函数拟合曲线见图6。

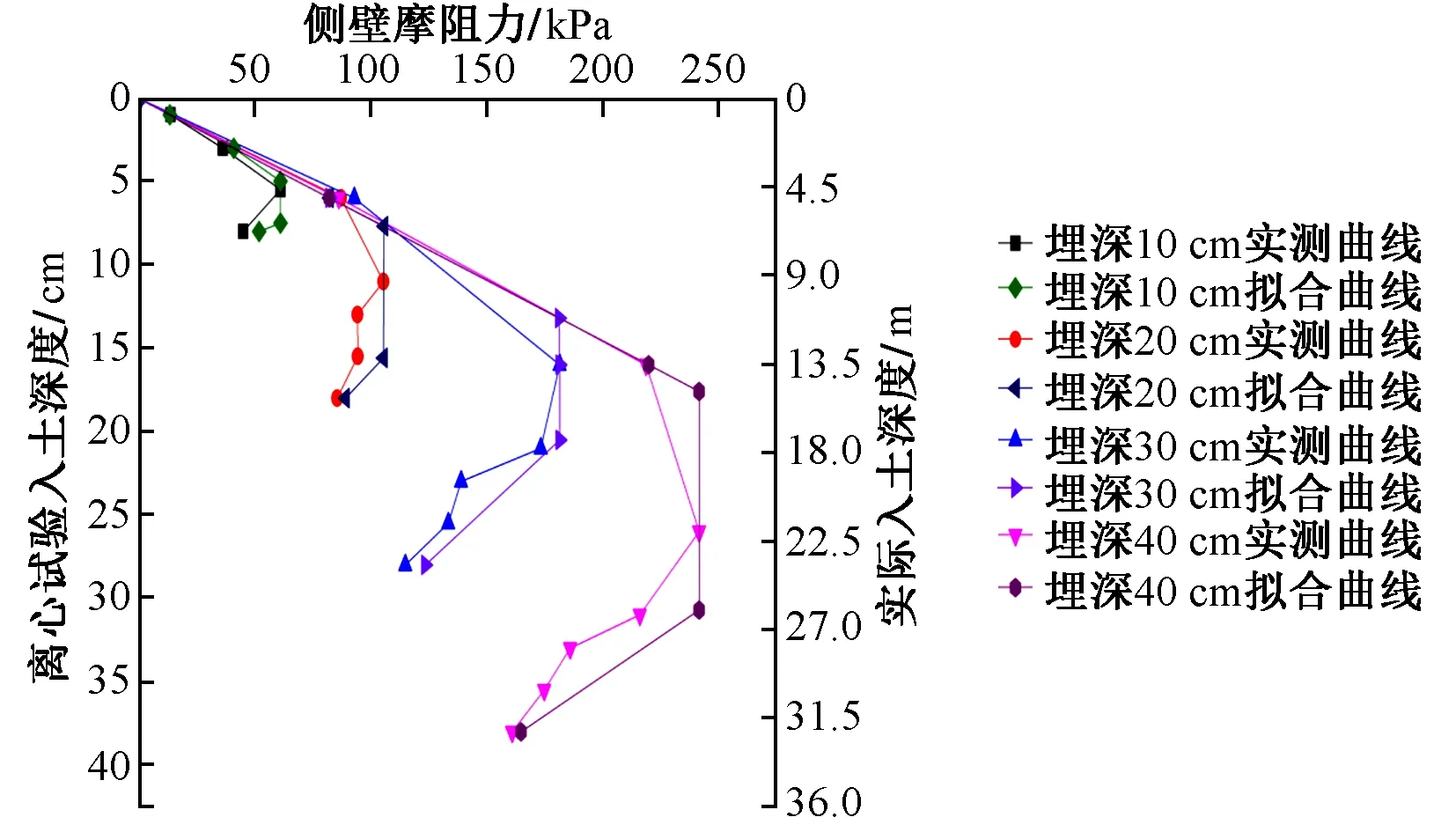
图6 不同埋深下沉井侧壁摩阻力分段函数拟合曲线

由图6可知：当h≤4H/9时，侧壁摩阻力随着深度的增加而线性增大至极限侧壁摩阻力；4H/9

4 结论

本文采用多功能数据自动化采集系统TLJ-2型土工离心机，对4组不同埋深下的沉井侧壁开展离心模型试验。通过对试验结果的分析，得到如下结论：

1)离心模型试验利用离心机产生的离心加速度场代替1g重力场，可使得模型与原型应力相等、应变相等，可以更好地模拟沉井下沉过程中侧壁摩阻力的大小及特性。

2)在一定的下沉深度范围内，沉井侧壁摩阻力随下沉深度的增加呈先增大后减小的趋势，且当入土深度为2/3倍沉井埋深时，沉井侧壁摩阻力达到极大值。

3)依据试验结果，分别采用抛物线、分段函数包络线形式对试验结果进行拟合，二者拟合程度均较高。考虑到工程应用的方便，选择分段函数作为侧壁摩阻力大小及分布计算模型，并给出了计算公式，可为今后类似工程提供参考。