摩擦摆支座隔震连续梁桥抗震分析的简化计算方法
李 健,邵长江
(1.中国铁路总公司建设管理部,北京 100844;2 西南交通大学 土木工程学院,四川 成都 610031)
桥梁通过在桥墩上设置减隔震支座等,将地震输入的动能转化为支座摩擦耗能和动能,从而减小了传递给桥墩的地震力,同时结构基本周期的延长使其远离了地震峰值加速度区段(从反应谱的角度看),降低了结构的动力响应[1-3]。由于减隔震支座能够显著改善结构的抗震性能,被广泛应用于强震区的桥梁工程中,是桥梁抗震设计中的重要减灾措施和研究课题。摩擦摆隔震(Friction Pendulum System,FPS)支座是Zayas等[4]提出的一种有效的干摩擦滑移隔震体系,它通过摩擦滑移件在球形凹面上的滑动进行隔震。摩擦摆隔震支座具有对地震激励频率范围低敏感性和抗震性能高稳定性的特点,特有的圆弧滑动面使其具有自复位功能,无需附设阻尼向心机构。与普通的摩擦滑移隔震支座相比,它很好地利用了摆的原理,通过上部结构的自重提供回复力,从而有效减小结构在震后的残余位移[5-8]。采用减隔震措施后的桥梁比延性桥梁的抗震计算方法复杂。基于此,本文通过建立摩擦摆隔震梁桥的简化模型,提出隔震连续梁桥的抗震简化计算方法,并通过对比分析有限元结果和简化计算结果来验证模型和算法的合理性。
1 摩擦摆支座隔震梁桥的简化算法
摩擦摆支座具有结构紧凑、物理模型简单、抗震机理可靠的优点。采用摩擦摆支座(见图1)的桥梁可以简化为质量弹簧力学系统(见图2)。

图1 摩擦摆支座示意
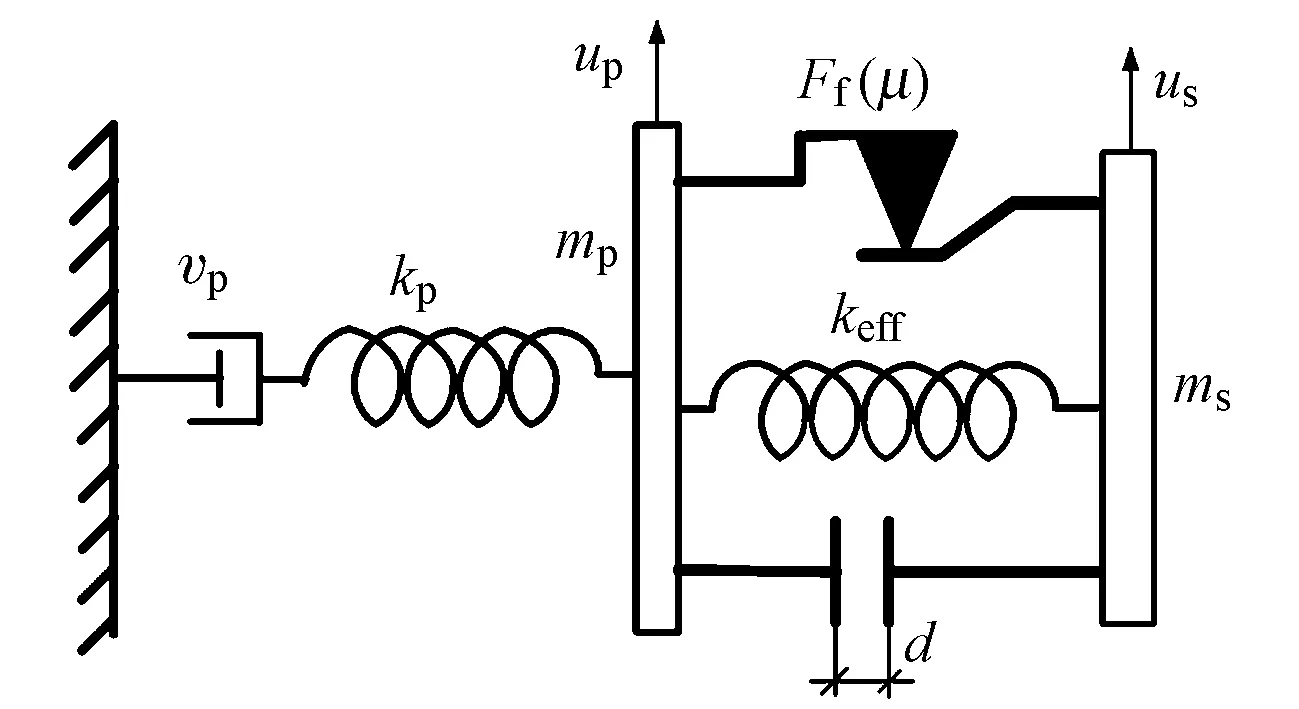
图2 摩擦摆支座系统简化模型
图2中:keff为摩擦摆的等效刚度;Ff(μ)为摩擦摆支座的摩擦力;d为摩擦摆支座的设计位移;kp为桥墩刚度;vp为桥墩结构的阻尼;mp和ms分别为桥墩和上部结构的质量。
小振幅摆动时,摩擦摆支座的侧向力F等于回复力Fe与摩擦力Ff之和[8],即
(1)
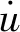
摩擦摆支座通过结构自重沿滑动曲面的切线方向的分力提供回复力,帮助上部结构回到原来的位置。如同普通钟摆一样,摩擦摆支座上部的结构也有一个振动周期,即
(2)
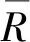
研究发现滑动面上的动摩擦因数与支座的运动形态相关,滑动摩擦因数的大小依赖于滑块的运动速度和曲面上的压力,表达式为
(3)
式中:μmax为滑动稳定时的最大摩擦因数,取0.06;μmin为速度极小时的摩擦因数,取0.02;a为速度相关系数,取20。
对结构进行反应谱或等效线性分析时,应将支座进行等效线性化处理,得到该支座的等效刚度和等效阻尼比[9],分别为
(4)
(5)
只要合理选取地震下支座的设计位移d、半径R和摩擦因数μ,就能满足不同的减隔震设计要求。设梁桥的第i个桥墩刚度为kp,i,单个桥墩与其上隔震支座的串联刚度为Keq,则纵桥向结构总体等效刚度为上述所有串联刚度的总和,即
(6)
主桥一联的换算质量Mt[9]为
Mt=Ms+ηpMp+ηbMb
(7)
式中:Ms,Mp,Mb分别为上部结构、桥墩和固定盖梁的质量;ηp,ηb分别为桥墩和盖梁的质量换算系数,计算时应考虑地基变形的影响。
由上述结构的等效刚度和换算质量可得结构的等效周期为
(8)
减隔震结构的等效阻尼比为
(9)
式中:di为第i个支座的设计位移;ξp,i为第i个桥墩的等效阻尼。
根据全桥结构有限元模型的动力特性计算结果,该结构基本周期为4.117 s,参照CJJ 166—2011《城市桥梁抗震设计规范》[9],当结构基本周期大于5.0Tg=1.65 s(Tg为特征周期)时,反应谱曲线为
S=2.25[0.02γη1-η2(T-5Tg)]Amax
(10)
式中:γ为反应谱曲线下降段的衰减指数;η1为反应谱直线下降段下降斜率调整系数;η2为阻尼调整系数;Amax为地震动加速度峰值。
由反应谱曲线和结构的等效周期可得到简化后的支座设计位移,即
(11)
隔震支座设计位移求解的迭代过程为:先设定摩擦摆的摩擦因数,根据式(2)得到支座的振动周期;由式(4) 和式(5)分别计算得到摩擦摆的等效刚度和等效阻尼比;根据式(6)和式(7)分别得到结构的等效刚度和等效质量;根据式(8)和式(9)分别得到结构的等效周期和等效阻尼比;根据式(10)得到等效结构的反应谱曲线。在此基础上由式(11)可以得到隔震结构的最大位移。当设计位移和最大位移的相对误差小于5%时,认为所得数值即为支座的设计位移。
2 工程概况及简化模型
2.1 工程概况
一大桥主桥部分桥跨布置为(61+108+61)m三跨连续梁桥(如图3所示),主梁采用变截面预应力混凝土箱梁,辅助结构的拱肋为钢箱截面,左右两幅主梁在桥墩处通过横梁连接。中支点处梁高6.5 m,跨中梁高2.5 m。主墩高9.0 m,过渡墩高15.0 m,主墩及过渡墩截面均为实心矩形双柱式桥墩,两墩柱通过系梁连接。基础采用群桩基础,中间墩桩长90.0 m,左边过渡墩桩长83.0 m,右边过渡墩桩长87.0 m。

图3 主桥立面及平面(单位:cm)
根据桥梁地勘报告,桥址场地为Ⅲ类场地。由桥址地震安全评价报告可知,桥址处于Ⅷ度设防区,桥址2000年重现期(E2水准)的地震峰值加速度为0.333 7g,潜在震源距30 km。摩擦摆支座的最大等效阻尼比为0.257(小于0.300)。有限元模型分析的基本振型为桥墩纵向弯曲,基本周期4.117 s,其质量参与系数为0.689。因此该桥沿纵向属于规则结构,可以采用简化算法分析桥梁结构的抗震性能。
2.2 结构抗震计算的简化模型
为了方便简化模型的建立,桩土效应通过现行规范中的M法计算桩周土的刚度,并作为弹簧施加在桩体上。根据沿墩顶顺桥向作用的单位力,分别求得各桥墩的纵桥向抗推刚度,同时给出各桥墩的换算质量,见表1。
为了得到抗震性能优良、设计方案经济的隔震支座参数,给出3种摩擦摆隔震支座设计方案,见表2。

表1 桥墩纵桥向抗推刚度和换算质量

表2 等效单自由度系统摩擦摆隔震支座的设计方案
由于规范要求结构隔震后的基本周期应该是隔震前结构的2.5倍以上[9],根据有限元模型计算得到未隔震结构的基本周期为1.74 s。由表2可知,当摩擦摆的半径为5.85 m时隔震结构的基本周期为4.067 s,可以满足要求。此时,结构的总体水平地震力Ehp=SMt=26 863 kN。根据桥墩刚度将水平地震力分配各个桥墩,可得到墩底的弯矩和竖向地震力。
根据桥梁结构设计参数建立SAP2000有限元模型进行非线性时程分析。摩擦摆支座参数取方案1,计算得到桥墩关键截面的地震响应,见表3。

表3 罕遇地震作用下关键截面的地震响应
注:轴力以受压为正。
由表3可知:简化算法得到的左右主墩墩底剪力和弯矩大于非线性有限元的数值,可使得主墩的抗震设计偏于安全;而左右过渡墩因为计算过程中忽略了相邻跨的影响,其剪力和弯矩简化计算结果小于非线性有限元的分析结果,故采用简化方法进行过渡墩抗震设计时,需采取有效措施适当增强其抗震能力。
罕遇地震作用下支座沿地震方向的位移响应见表4。简化计算得到的支座位移设计值为0.52 m(参见表2),对比表4发现支座的位移响应小于位移能力,说明支座设计是合理的。

表4 罕遇地震作用下支座沿地震方向的位移响应 m
3 结论
1)本文给出的简化计算公式具有较高的精度,能够较好地反映结构纵向的地震需求和考虑结构的基本特性,可以用于规则连续梁桥的初步抗震设计。
2)摩擦摆支座设计位移除了受自身参数(如摆的半径、摩擦系数等)影响外,还需考虑桥梁墩刚度、基础以及地震强度的影响。有限元模型计算的位移响应表明,支座的设计位移能力能够满足罕遇地震下的支座位移需求。

