非一致激励下大跨度铁路斜拉桥地震响应规律

黎 璟，杨华平，钱永久，龚婉婷

(1.西南交通大学 土木工程学院，四川 成都 610031；2 四川省交通勘察设计研究院有限公司，四川 成都 610017)

在同一场地震下，地震波的幅值、相位及频谱特性存在与场地相关的空间变异性，通常体现为弱相干效应、行波效应和局部场地效应[1]。其中，行波效应导致地震波到达桥梁各支承处的时间存在滞后效应，结构体系受到的激励不同步，其地震响应特征与一致激励有明显差异[2]。因此大跨桥梁抗震设计过程中通常需要进行非一致激励分析来研究行波效应的影响。

近年来，研究者们针对非一致激励下结构的地震响应规律展开了一系列研究。武芳文等[3]以苏通大桥为工程背景，比较了一致激励与非一致激励下结构地震响应的区别，指出了大跨度斜拉桥抗震设计过程中考虑非一致激励的必要性。方诗圣等[4]讨论了行波效应视波速与结构地震响应之间的关联，结果表明随着视波速的增大，行波效应对结构地震响应的影响逐渐减弱。黄小国等[5]分析了4个相位差范围内大跨度桥梁地震响应的规律，认为结构内力响应随相位差的增大呈增加趋势。许智强等[6]则研究了叠合梁斜拉桥在非一致激励作用下的地震响应特性。

尽管目前关于非一致激励下桥梁地震响应规律的研究已取得了一定的进展，然而主要局限于分析视波速在行波效应中的作用，鲜见对广泛相位差区间内非一致激励的探讨，且缺乏指导桥梁工程抗震设计的实用性建议。本文以一座主跨228 m的高速铁路钢桁梁斜拉桥为工程背景，采用大质量法分析不同相位差下结构的动力响应，建立相位差与结构自振周期之间的关联，探讨斜拉桥地震响应受行波效应影响的变化规律，提出适用于工程结构抗震设计的建议。

1 工程概况与计算模型

1.1 桥梁概况

一座双塔钢桁梁斜拉桥全长492 m，跨径布置为(36+96+228+96+36)m，设计速度250 km/h，线间距4.6 m。采用宝瓶形钢筋混凝土索塔，塔高105 m，两主塔分别为1号塔和2号塔。主梁为钢桁梁，梁宽15 m，桁高14 m，节间长度12 m。全桥为板桁组合结构，上下弦杆采用箱形截面，斜腹杆及横向连接系为H形截面，下弦平面采用正交异性板的整体道砟桥面结构。每3 m设置1道横梁，纵梁全桥连续，共设置5道。桥塔与主梁间设置纵向活动支座，辅助墩上的支座均为纵向活动支座，全桥在纵向为半漂浮体系。桥型总体布置如图1所示。

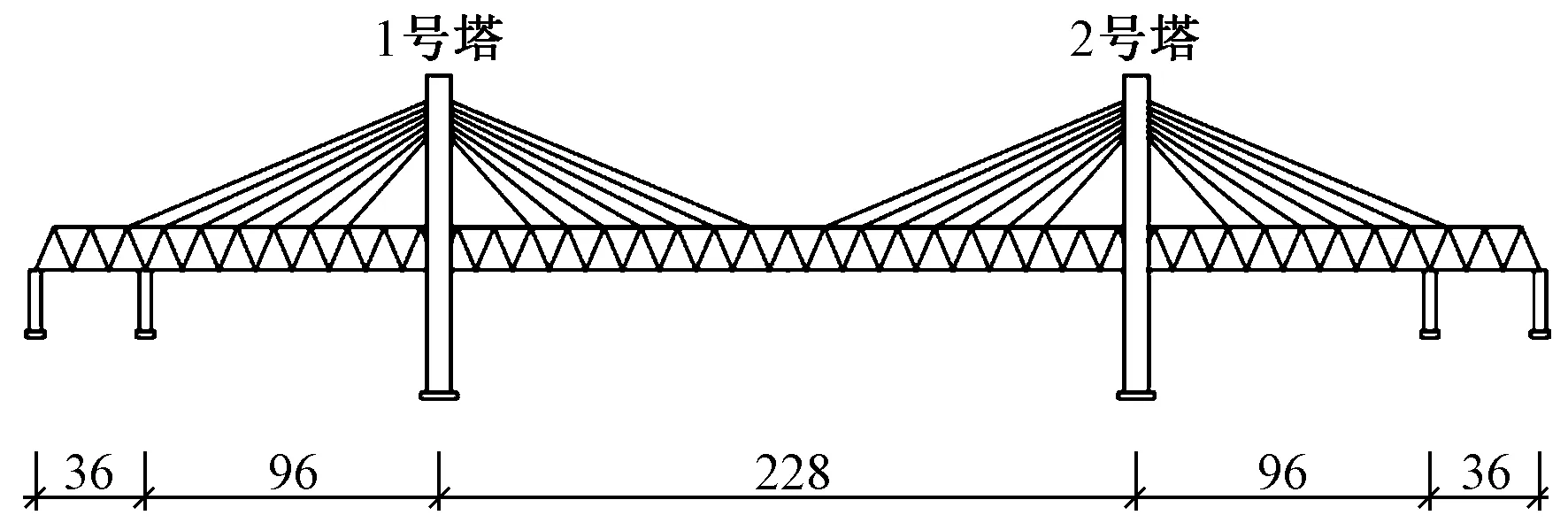
图1 桥型总体布置(单位：m)

1.2 结构有限元模型

大质量法[7-8]是进行非一致激励下大跨度结构动力响应分析的有效方法，在工程实践中得到广泛应用。本文采用有限元软件SAP2000建立了基于大质量法的动力分析模型，其中主梁钢桁架体系及混凝土桥塔采用空间梁单元模拟，斜拉索采用空间索单元模拟，桥面板采用板壳单元模拟，与主桁架刚性连接，桥墩墩底固结，主梁与主塔之间用弹性连接模拟纵向活动支座。全桥共 6 205 个单元，其中空间梁单元 4 501 个，索单元64个，板壳单元 1 640 个。动力分析模型如图2所示。

图2 动力分析模型

采用子空间迭代法计算结构振动特性，前5阶振型及周期见表1。

表1 前5阶振动特性

1.3 地震波选取

桥址位于8度区二类场地，设计地震下峰值加速度为0.2g。从NGA-West2数据库中选取了地表以下30 m深度范围内土层平均剪切波速VS30处于260～500 m/s，矩震级范围为6.9～7.1，加速度峰值(Peak Ground Acceleration,PGA)接近0.2g的7条地震动记录，通过乘以调幅系数将各波加速度峰值统一调整至0.2g后用于分析。各地震动记录特性见表2。

表2 地震动记录特性

2 行波效应影响规律

地震作用下结构的动力响应与自身动力特性密切相关，而行波效应对结构动力响应的影响主要源于相位差引起的拟静力项[9]。因此，建立相位差Δt与桥梁一阶纵向自振周期T之间的关联，并探讨Δt为0.1T～2.2T时桥梁在纵向非一致激励下的动力响应规律，每间隔0.1T进行1次动力分析。

2.1 塔顶位移分析

纵向一致激励下斜拉桥主塔塔顶位移响应峰值为u0，相位差纵向非一致激励下位移响应峰值为u。不同相位差下两主塔塔顶位移响应比值见图3。

由图3可见：两主塔塔顶位移响应比值均随Δt呈周期性变化，且变化周期与结构一阶自振周期T基本一致。在Δt为0.5T和1.5T时，塔顶位移响应达到谷值；在Δt为1.0T和2.0T时，塔顶位移响应达到峰值。同时，在Δt为0.5T时，各地震波计算结果取均值后，两桥塔塔顶的位移响应值仅为一致激励时的7.3%和6.2%；在Δt为1.5T时，两桥塔塔顶的位移响应值为一致激励时的31.9%和32.3%。可见在非一致激励下，相位差为结构自振周期(2n+1)/2倍(n为整数)时，桥梁位移响应值会极大降低。因而在进行结构抗震设计时，综合调整桥梁主跨跨径及自振周期，使得地震波到达主墩之间的时差尽量接近结构自振周期的(2n+1)/2倍，对控制结构的位移响应极为有利。此外，u/u0均小于1。对于纵向漂浮体系斜拉桥，纵向非一致激励可以减小结构位移响应，相位差效应有利于控制主塔位移。

图3 不同相位差下两主塔塔顶位移响应比值

2.2 墩底弯矩分析

纵向一致激励下斜拉桥墩底纵向弯矩响应峰值为M0，相位差非一致激励下墩底纵向弯矩响应峰值为M。不同相位差下两主墩墩底弯矩响应比值见图4。

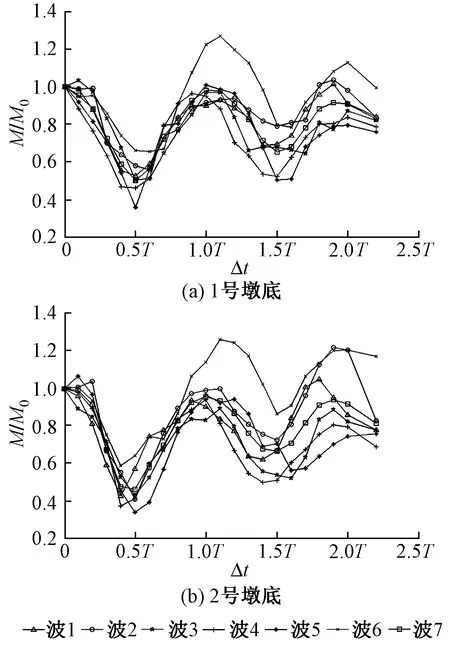
图4 不同相位差下两主墩墩底弯矩响应比值

由图4可见，主墩墩底弯矩响应峰值随Δt的变化具有周期性，且变化周期与结构自振周期大小基本相同。墩底弯矩响应在Δt为0.5T和1.5T时达到谷值，而在Δt为1.0T和2.0T时达到峰值。Δt=0.5T时，各地震波计算结果取均值后，两桥墩墩底的弯矩响应值为一致激励时的51.9%和45.8%；Δt=1.5T时，两桥墩墩底的弯矩响应值为一致激励时的67.3%和61.1%。与位移响应分析规律相一致。说明在结构抗震设计中，控制相位差接近结构自振周期的(2n+1)/2倍可以有效降低结构内力响应。

当Δt为0.1T～2.2T时，非一致激励下弯矩响应峰值最大可达一致激励时的1.26倍。对于大跨度结构抗震设计，仅进行一致激励分析可能会低估结构的内力响应，因此有必要进行非一致激励计算。为节省计算量，可分析相位差为自振周期整数倍的情况。

3 结论

1)非一致激励下塔顶位移响应峰值与墩底弯矩响应峰值均随相位差呈明显周期性变化，同时变化周期与结构一阶自振周期基本相同。在相位差为自振周期的(2n+1)/2倍时结构的动力响应最小，在相位差为自振周期的整数倍时结构的动力响应最大。

2)由于行波效应下结构动力响应与相位差存在明显的相关性，控制相位差与结构自振周期比值能有效调整结构动力响应。在结构抗震设计中，可参考特定场地条件下的剪切波速及最危险临近潜在发震断层的位置及走向，综合调整主跨跨径与结构自振周期，使地震波到达两主墩的时差接近结构自振周期的(2n+1)/2倍，降低结构地震响应。

3)非一致激励可能会增大结构地震内力响应，在对大跨度桥梁进行抗震设计时，行波效应影响不可忽略，应当分析相位差为结构自振周期整数倍的情况以控制设计。

近年来，我国建成的铁路钢桁梁斜拉桥多在塔梁间设置纵向黏滞阻尼器，其约束体系与本文半漂浮体系之间有明显区别，动力响应特征也存在一定差异，在非一致激励下半漂浮体系斜拉桥的地震响应规律尚不明确，有待后续研究探讨。