Closed-Form and Analytical BER Expression for OFDM System with μ-Law Companding Operation

Zhitong Xing＊,Kaiming Liu,Yuan'an Liu

Institute of Smart Wireless Information Technology,Beijing University of Posts and Telecommunications,Beijing 100086,China

Abstract: The μ-law companding function has been applied widely in orthogonal frequency division multiplexing (OFDM) to reduce the peak-to-average power ratio (PAPR).However,nonlinear distortion caused by the μ-law companding function is considered a key impairment in OFDM communication systems.Few studies have addressed theoretical nonlinear distortion caused by μ-law companding function for OFDM systems.In this paper,we derive a closed-form expression of signal distortion as well as the closed-form bit error rate (BER) of OFDM system caused by the μ-law companding function.Based on the theoretical signal distortion and BER expression,the theoretical BER value and signal distortion value can also be calculated,which can guide us to choose appropriate μ value for different BER condition and bit-to-noise (Eb/N0) condition efficiently.Then the PAPR performance can also be predicted.The results show good agreement on the Monte-Carlo simulation results and the obtained theoretical BER results.Furthermore,based on theoretical signal distortion and theoretical BER expression,the figure of the relationship among BER value,Eb/N0 and μ is also given.Based on this figure,we can find the appropriate μ law for different BER and Eb/N0 condition.And then the PAPR performance can also be predicted.

Keywords: OFDM; PAPR; nonlinear companding function; μ law companding scheme

I.INTRODUCTION

Orthogonal frequency division multiplexing (OFDM) has received interest in the challenging new spectrum use scenarios,such as cognitive radio (CR) and opportunistic dynamic spectrum access.However,despite its advantages,the inherent drawback of the long tail effect of the Rayleigh distribution obeyed by the OFDM signal amplitude leads to a wide range of OFDM signal amplitude fluctuations.It can cause the amplitude of OFDM signals to suffer from high peak-to-average power ratio (PAPR) [1,2].High PAPR may cause serious performance degradation with a nonlinear high-power amplifier at the transmitter.

In order to address the high PAPR problem,several techniques have been developed.The PAPR reduction schemes can be divided roughly into three categories.

The first is to reduce the probability of the emergence of a large PAPR signal.This type of method gives priority to reducing the PAPR by signal perturbation,taking selective mapping [2] and partial transmit sequence [3] as typical examples.

The second type of PAPR reduction method is the coding techniques.Code used for error detection and correction,such as linear block code,Golay sequences,and Turbo Codes [14-16] are desirable options to perform PAPR reduction.

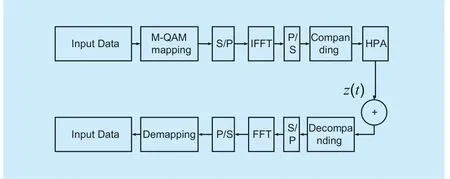
Fig.1.The diagram of OFDM modulation.

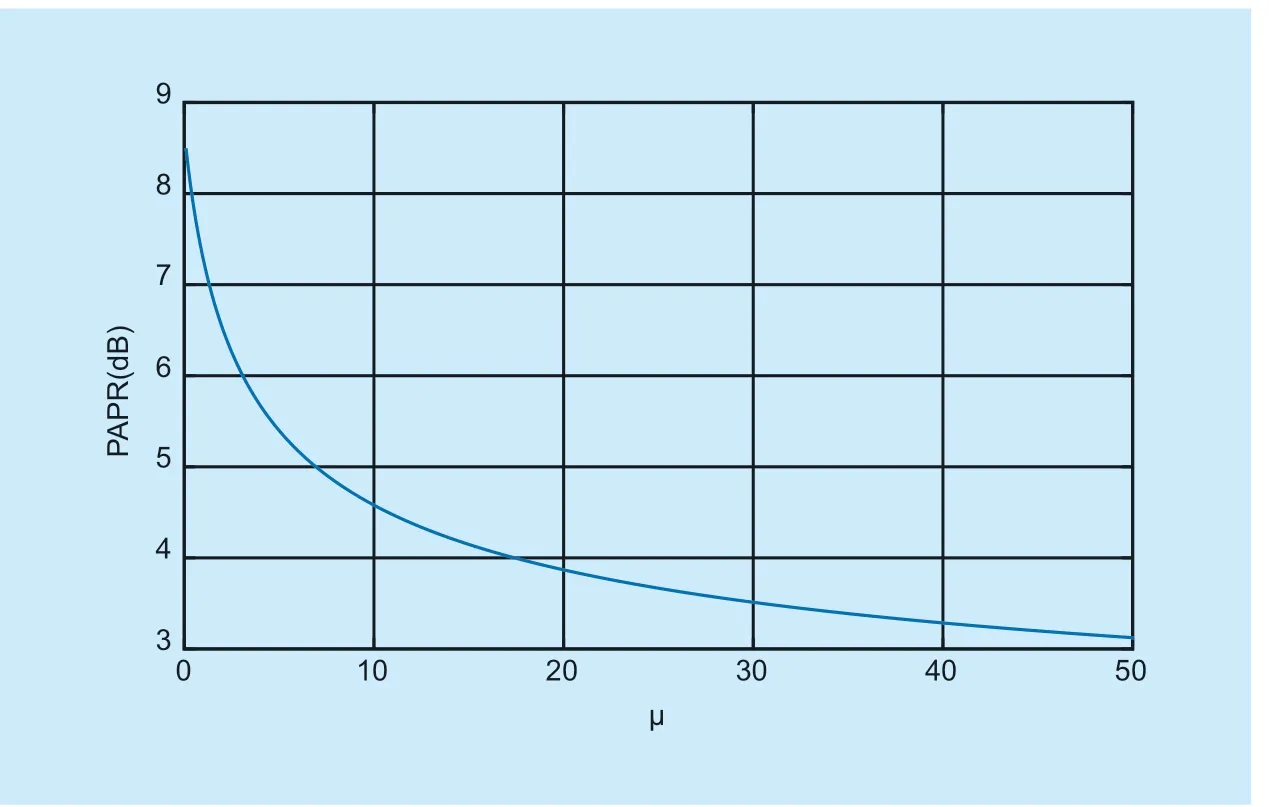
Fig.2.The PAPR performance for different μ.

The first two types of PAPR reduction method require large-complexity computation,which may not be suitable when the number of subcarriers is large.Performing a companding operation after multicarrier modulation may be an option.Among all the companding schemes,the most widely applied method is clipping [5].However,the clipping method introduces extra noise,which greatly affects the bit error rate (BER) and the out-ofband (OOB) of power spectral density (PSD).Subsequently,people designed linear companding schemes [6-8] to reduce the PAPR of OFDM.In previous work [6,7],the authors provided linear companding functions with several inflection points,and a different signal amplitude was companded with different scales.In other work [8],the authors provided a two-piecewise linear companding scheme.It transforms a small signal amplitude with a scale and a large signal amplitude with both a scale and a shift.It can maintain the same signal power before and after companding and obtain one-to-one mapping.Elsewhere [21,23-25],the authors employed minimum mean square error to issue the parameters of the companding function,which minimizes the companding distortion.Apart from the linear companding function,the nonlinear companding function is also an option to reduce the PAPR of OFDM signals.In previous research [9],Wang first proposed theμ-law companding (MC) scheme to reduce the PAPR.However,the MC increases the average power of the OFDM signal.In other work [15],a modification of MC,called “root based MC” (RMC),was provided to reduce the PAPR of the OFDM signal.RMC can guarantee the average power conservation.In previous work [16],the authors provided a function called amplitude limiting companding (ALC) scheme,which used polynomials to compress the signal amplitude.In fact,the companding function converts the amplitude of the OFDM signal from Rayleigh distribution to another probability distribution.Therefore,to find an appropriate nonlinear companding function [10-13],assigning a probability density function (PDF) of the OFDM signal amplitude after companding is also an alternative method.The nonlinear companding function is found based on the original signal PDF and assigned signal PDF.

Among all the PAPR reduction schemes,the nonlinear companding function is attractive owing to its high PAPR reduction ability and low-complexity calculation.Theμ-law companding function proposed in [10] and some modifications thereto [7,8] have been widely applied.Despite the wide use ofμ-law companding function,the closed-form BER expression of an OFDM system with aμ-law companding function has not been presented.

In this paper,we aim to analyses the effect of the signal distortion caused by aμ-law companding function,which causes BER performance degradation of OFDM systems.The theoretical relationship betweenμand signal distortion is derived.Based on the theoretical distortion value,the closed-form BER expression is also given.According to theoretical signal distortion and theoretical BER expression,we plot the figure for the relationship among BER value,Eb/N0andμ.Then appropriateμvalue can be chosen for different BER andEb/N0condition efficiently.In addition,the PAPR performance can also be predicted.

The organization of our paper is follows.Section II presents the system model of an OFDM system and theμ-law nonlinear companding function,which is used to reduce the PAPR.In section III,we detail the derivation of the closed-form signal distortion and closed-form BER.The figure of the relationship between theoretical signal distortion andμvalue is also given.In section IV,based on the theoretical BER expression,Numerical results are presented.Furthermore,the relationship among BER,Eb/N0andμ.is also presented.Then for appropriateμvalue,we can predict the PAPR performance.Finally,conclusions are given in section V.

II.SYSTEM MODEL

We consider OFDM systems (Figure 1) that are modulated by data symbols taken from theM-QAM constellation.The discrete-time transmitted OFDM signal is given by

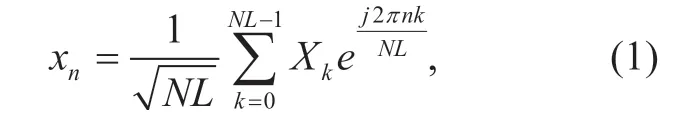
where

Considering the polar coordinates of (1),we can write

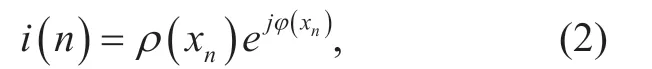
whereρ(xn) andφ(xn) are the modulus and phase ofxn,respectively.In general,ρ(xn) obeys the Rayleigh distribution,of which the PDF can be represented as

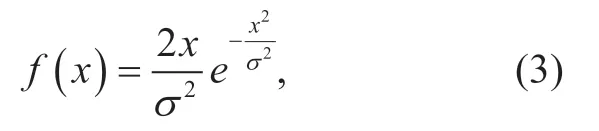
whereσ2is the average power of the OFDM signal.Without loss of generality,the average power of the OFDM signal is normalized to one.Then,equation (3) can be written as

The PAPR of the transmitted signal can be expressed as

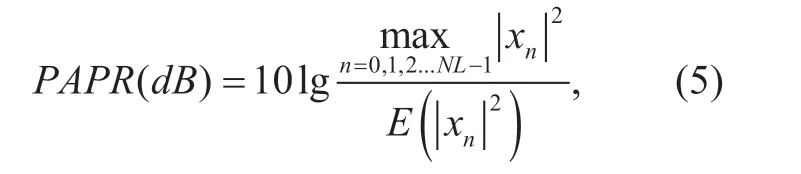
In the transmission chain,theμ-law companding function is used to reduce the PAPR of OFDM signals.The signal at the output of theμ-law companding function can be expressed as

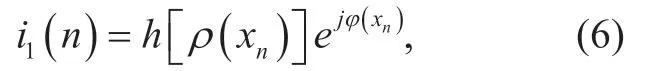
whereh(.) denotes theμ-law companding function being expressed as

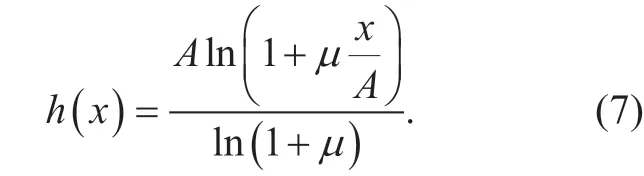
In equation (7),xis the amplitude of the OFDM signal andAis a normalization constant such thatThis means that

Theμ-law companding function causes an increase in the average power.In order to constrain the signal before and after to companding to the same power level,a normalization factoris applied after theμ-law companding function.Then,(7) can be rewritten as

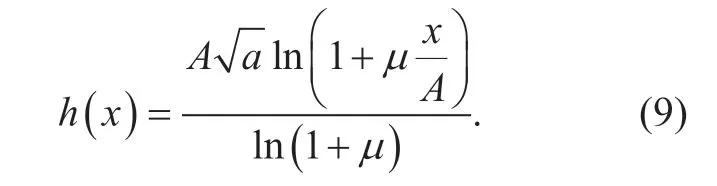
Figure 2 shows the PAPR performance for differentμvalues.From Figure 2,we observe that the PAPR value will decrease with the increasing ofμ.

In order to evaluate the signal distortion caused by theμ-law companding function,the authors in [11] demonstrated that the transmission of a fixed symbol can be modeled as

whereb(n) is an additive zero-mean noise with variancePbn,which is not correlated toi1(n) andαis attenuation value.Obviously,

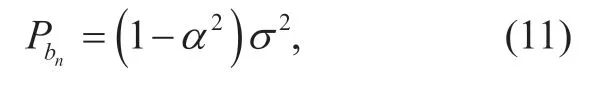
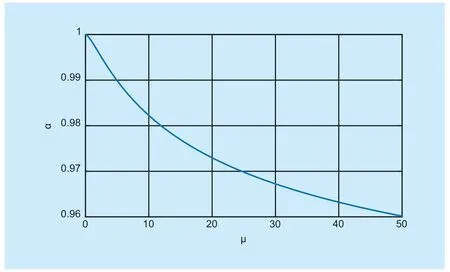
Fig.3.The relationship between μ and α.

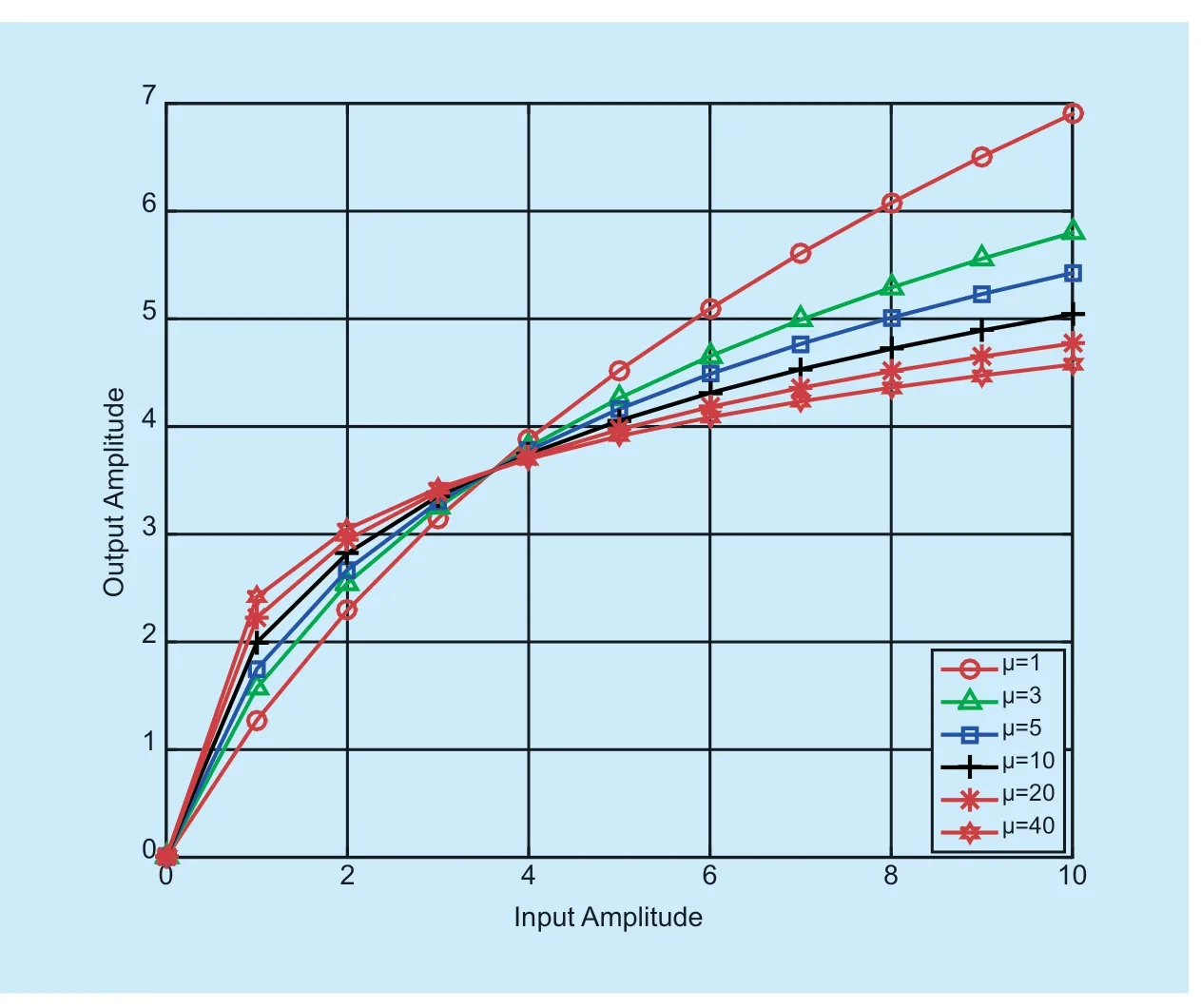
Fig.4.The nonlinear companding curve for different μ.

Equation (10) means that the companded signal can be modeled as the aggregate of an attenuated signal component and compandeing noisePbn.Soαis also the representation of signal distortion.Furthermore,according to [11],α≤1 and the closerαto 1,the smaller the signal distortion will be.

When passing through an Additive White Gaussian Noise (AWGN) channel,equation (10) can be rewritten as

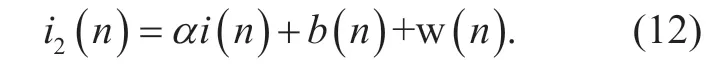
Obviously,at the decision end,signal to noised ratio (SNR) can be written as

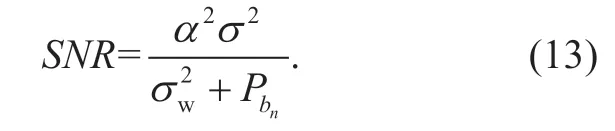
Substituting equation (11) into (13),the SNR can be written as

In an AWGN channel,considering the orthogonality of OFDM system,the relationship between BER and SNR is [27,28]

whereQ() is the Q function.The theoretical BER expression for OFDM is equal to QPSK.The computation of the BER requires a determination ofα.According to [6],αcan be represented as

The key problem to derive theoretical BER expression in (15) is to derive the integral in (16).The deriving of (16) can help us know the theoretical value of BER as well as theoretical signal distortion for differentμvalue.This can help us know the BER performance for differentμvalue,which can guide us to choose appropriateμvalue.

III.PERFORMANCE ANALYSIS

In this part,we derive the closed-form expression ofαfor an uncoded QAM-based OFDM signal using aμ-law nonlinear companding function.αof (16) can be obtained by substituting (4) and (9) into (16).Furthermore,the logarithmic functiony=ln(1+x) can be written as a Taylor expansion

with the convergence domain [-1,1].Then,for theμ-law companding function,the signal amplitudexshould satisfy

Based on this,the calculation ofαdepends on the value ofμ.

a.μ≤1

In this case,all of the signal amplitudes are in the convergence domain,then,∀0,the Taylor series expansion of theμ-law companding function is given by

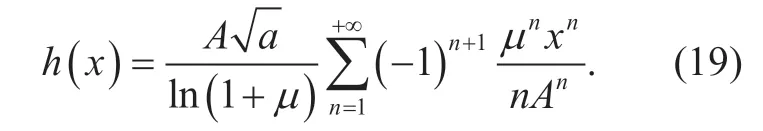
Substituting (19) into (16),we obtain

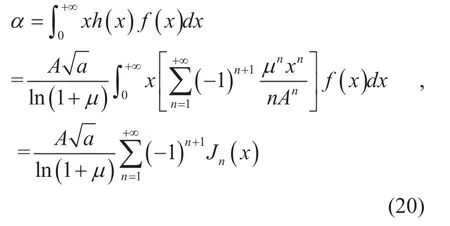
where

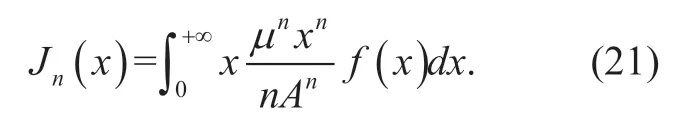
Table I in the Appendix shows for different valuen,the corresponding value ofJn(x).

Although calculating the infinite series summation ofJn(x) is difficult,we can approximateαby rewriting the infinite series summation in (20) to finite series summation,which can be represented as

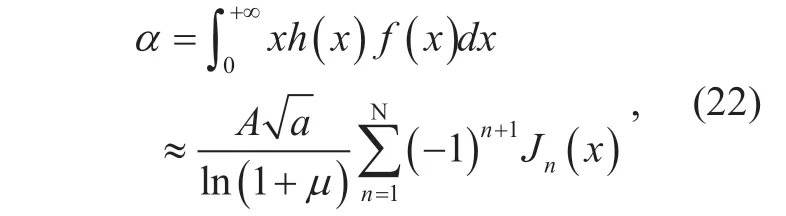
whereNindicates the number of items we have taken in the series in (21).

b.μ＞1

In this case,the integral in (16) can be separated as

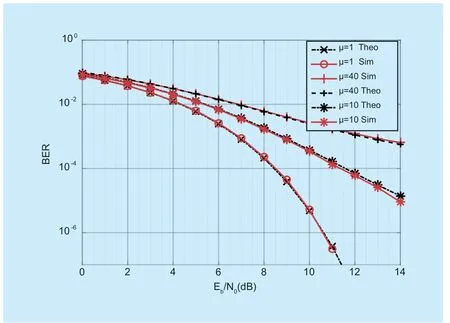
Fig.5.The BER vs Eb/N0for μ law companding function for OFDM system,N=64.

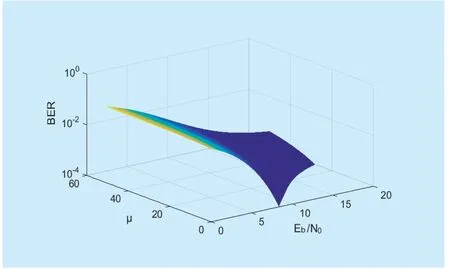
Fig.6.The relationship between Eb/N0,BER and μ value.

For the first summation term in (22),the amplitude value is in convergence domain,such that the integralcan be written as

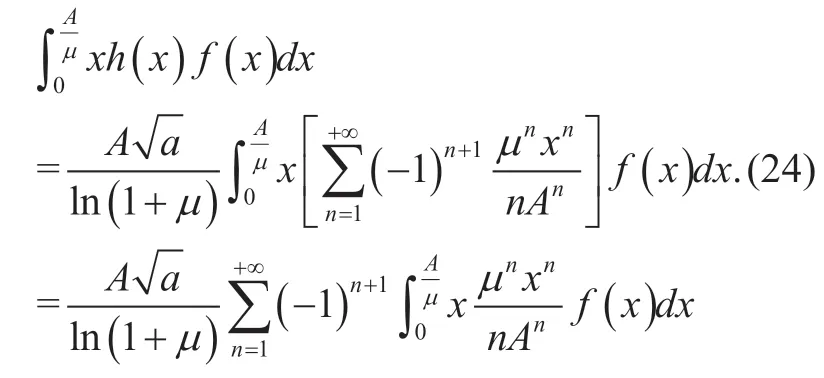
We further assume that

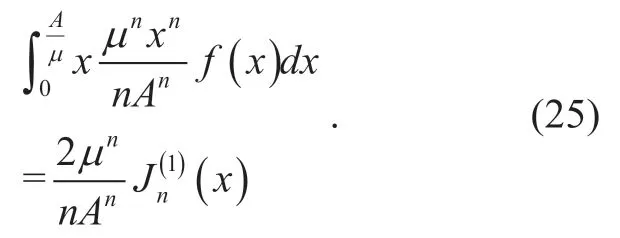
Similarly,the infinite series summation in (24) can also be simplified as a finite series summation.Table II in Appendix shows for different value ofn,the corresponding value of(x).

For the second summation term in (22),the integral

cannot be calculated in a closed form.Therefore,we consider calculating the numerical value [22] for equation (26).

Considering that

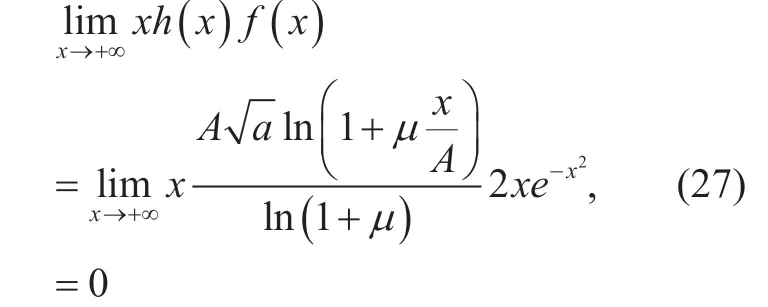
so ifxis enough large,xh(x)f(x)≈0.This means that we can use definite integral to approximate infinite integral in (26) with

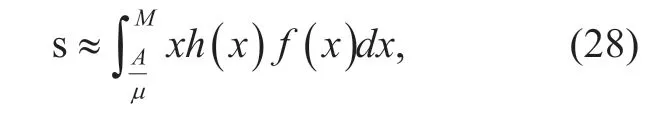
whereMis a sufficient large number.The numerical integral can be calculated by using rectangular method [22].

We divide the domain [A/μ,M] intoLpieces,then the integral can be regarded as the sum of the small rectangular areas.For theith piece of small rectangular,the length is (M-A/μ)/Lwhile the width isxih(xi)f(xi).So the area for the ith small rectangular is

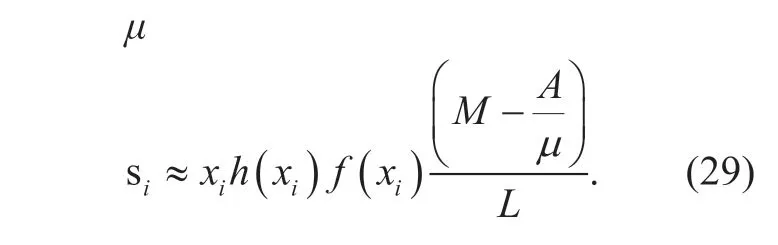
So the total numerical integral is

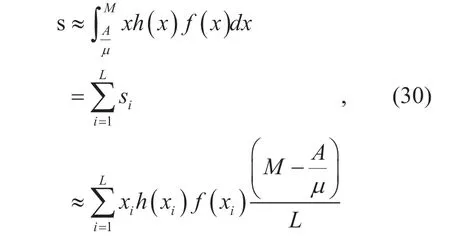
where

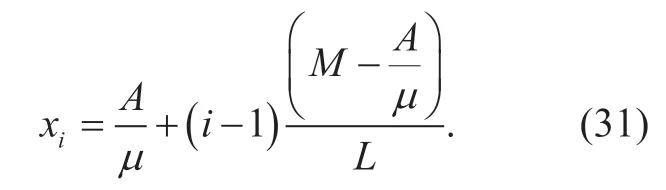
Having completed the calculation ofα,we can calculate the theoretical closed-form BER expression as well as the BER upper bound by substituting (20) or (30) into (14) and (15).

Figure 3 shows the relationship betweenμandα.It can be obtained that an increase inμleads to a decrease inα.This means that increasingμvalue will make the BER performance decrease.The reason why a largeμvalue will make the BER performance decrease can be found in figure 4.In figure 4,we can find that whenμis large,the curvature of theμlaw nonlinear companding function is large.This will make the OFDM signals after nonlinear companding suffer from large nonlinear signal distortion.

IV.SIMULATION RESULTS

In this section,the closed form expression in (20) and the upper bound of the BER performance related with (30),as well as the simulation results are presented.We consider OFDM systems withN=64 subcarriers.For the nonlinear companding function,we choose theμ-law companding function,andμ∈{1,10,40} to represent different cases ofμ.It should be noted that this study is valid for any value of nonlinear compandingμ.Figure 5.Shows an evaluation of the closed-form BER expression given related with (20),(30) and (15).For each value ofμ,we can see a very good agreement between the Monte-Carlo simulation results and those obtained analytically by using (20),(30) and (15).We can also underline that for a given value ofμ,the number of terms required in the infinite series of (20) and (30) should be even.Only a few terms can have negligible loss in precision.

Furthermore,figure 6 plots the relationship among BER,Eb/N0andμvalue.From the figure,we can find that whenEb/N0becomes larger,the BER will decrease for a certainμvalue.And an increasing ofμvalue will cause the increasing of BER.Table III in the appendix shows the value of BER whenEb/N0is 10dB.The PAPR value is also presented for differentμvalues.

V.CONCLUSION

In this study,we investigated the impact of a nonlinear companding function on the performance of an OFDM system.We derived a closed-form BER expression for an OFDM system passing through aμ-law nonlinear companding function.From the simulation results,we found that the theoretical value coincides with the simulated value.Furthermore,based on the theoretical signal distortion and theoretical BER expression,the relationship figure among BER,Eb/N0andμvalue has been plotted.From the figure,we can find the appropriateμvalue for a certain BER constraint.And the PAPR can also be predicted.

Appendix

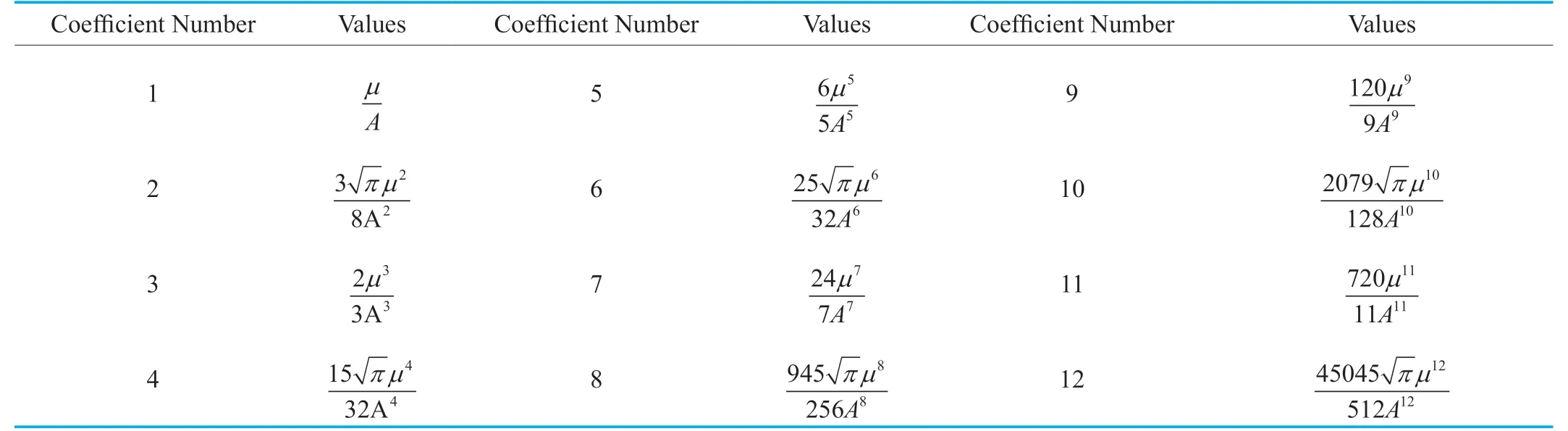
Table I.The value of Jn(x) for different terms

Table II.The value of x ()for different terms.

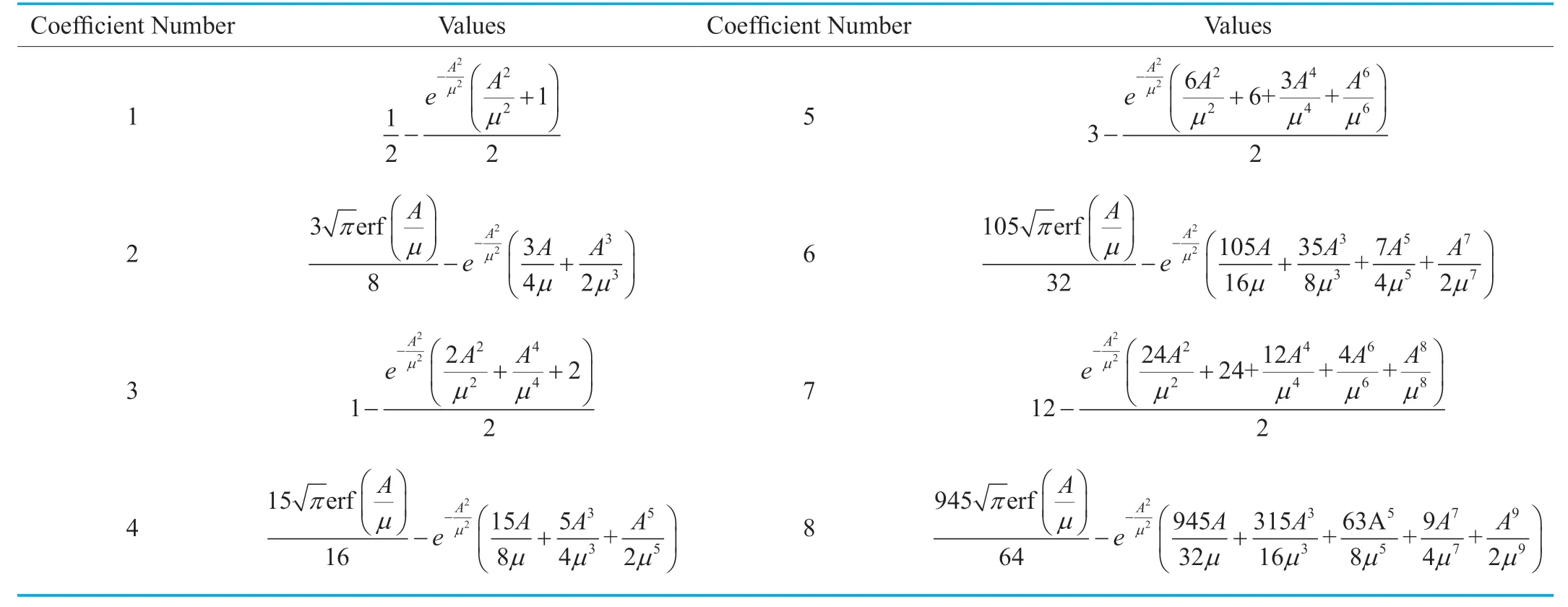
Table II.The value of x ()for different terms.

Coefficient Number Values Coefficient Number ValuesA2A2e-µA2 2■ ■■ ■■ ■µ2 4 6 2+1 5e-µA A A 1 1 2 4 6-3-2■ ■■■■■6 3µ µ µ2 2+6+ +2 2 3 erfπ 8A2A 3A A3■ ■■ ■■ ■µ- +e-µ2■ ■■ ■■ ■4 2 3µ µ6A2A 105 erfπ 32 16 8 4 2 3 5 7 105 35 7µµµµ■ ■■ ■■ ■µ-e-µ2■ ■■ ■■■A A A A++ +3 5 7 3A2e-µ2 4 2A A 2 4 1-2■ ■■■■■µ µ+ +2 7 2A2e-µ2 4 6 8A A A A 24 12 4µ µ µ µ2■ ■■■■■2 4 6 8 12-+24+ + +2 4A2A 15 erfπ 16 8 4 2A A A3 5■ ■■ ■■ ■µe-µ- +2■ ■■■■■15 5µµµ+3 5 8A2A 3■ ■■ ■■ ■µ945 erfπ 64 32 16 8 4 2-e-µ5 7 9 2■ ■■■■■945 315 63A 9µµµµµA A A A+3+ + +5 7 9

Table III.BER and PAPR Values for different μ in Eb/N0=10dB.

ACKNOWLEGDEMENT

This work is supported by the National Natural Science Foundation of China(61821001/61272518).