Constructing Certificateless Encryption with Keyword Search against Outside and Inside Keyword Guessing Attacks

Yang Lu＊,Jiguo Li

1 School of Computer Science and Technology,Nanjing Normal University,Nanjing 210023,China

2 College of Mathematics and Informatics,Fujian Normal University,Fuzhou 350117,China

3 Fujian Provincial Key Laboratory of Network Security and Cryptology,Fuzhou 350007,China

Abstract: Searchable public key encryption is a useful cryptographic paradigm that enables an untrustworthy server to retrieve the encrypted data without revealing the contents of the data.It offers a promising solution to encrypted data retrieval in cryptographic cloud storage.Certificateless public key cryptography (CLPKC) is a novel cryptographic primitive that has many merits.It overcomes the key escrow problem in identity-based cryptography (IBC) and the cumbersome certificate problem in conventional public key cryptography (PKC).Motivated by the appealing features of CLPKC,several certificateless encryption with keyword search (CLEKS) schemes have been presented in the literature.But,our cryptanalysis demonstrates that the previously proposed CLEKS frameworks suffer from the security vulnerability caused by the keyword guessing attack.To remedy the security weakness in the previous frameworks and provide resistance against both inside and outside keyword guessing attacks,we propose a new CLEKS framework.Under the new framework,we design a concrete CLEKS scheme and formally prove its security in the random oracle model.Compared with previous two CLEKS schemes,the proposed scheme has better overall performance while offering stronger security guarantee as it withstands the existing known types of keyword guessing attacks.

Keywords: searchable public key encryption; certificateless encryption with keyword search; inside keyword guessing attack; outside keyword guessing attack; random oracle model

I.INTRODUCTION

With the rapid development and widespread application of cloud computing,there is an emerging trend that increasingly more users are beginning to use the cloud for online data storing and data sharing.To protect the confidentiality and privacy of personal data,a user may encrypt his/her data.Because the cloud storage server does not know the corresponding decryption keys,the data confidentiality and privacy is guaranteed.However,the conventional encryption technique makes it very difficult to retrieve data in cloud storage.One common solution is that the user downloads all his/her encrypted data from the cloud storage server and decrypts them all regardless of what data he/she is searching for.Obviously,it is extremely inefficient due to the high cost of network transmission and the heavy overhead at the user devices.

In 2000,Songet al.[1] introduced the notion of searchable encryption.The searchable encryption mechanism enables an untrustworthy storage server to retrieve the encrypted data while keeping the data contents secret.Therefore,it offers a promising cryptographic solution to the problem of encrypted data retrieval.In [1],Songet al.presented a searchable symmetric encryption (SSE) scheme.However,SSE inevitably suffers from the key distribution and management problems due to the property of symmetric cryptography.In Eurocrypt’04,Bonehet al.[2] brought forth the notion of public key encryption with keyword search (PEKS) and the first PEKS scheme.PEKS allows the users to execute keyword search queries on the encrypted data generated by a standard public key encryption (PKE) system.In PEKS,three types of entities are involved:a sender,a server (also called a tester) and a receiver.The sender employs a PKE scheme to encrypt the data to be sent and then a PEKS scheme to produce a keyword ciphertext which is appended to the encrypted data.Both the data ciphertext and the keyword ciphertext are generated by using the receiver’s public key.In order to execute search queries on the encrypted data,a receiver generates and sends the server a keyword trapdoor in which the search keyword is encoded.After receiving the keyword trapdoor,the server tests whether the keyword in the keyword trapdoor is the same as that in the keyword ciphertext without seeing the plaintext of the data and the search keyword.Finally,the server returns the receiver all encrypted data that contain the search keyword.Since its introduction,PEKS has aroused great attention in the research community.So far,numerous PEKS schemes and variants have been presented in the literature,e.g.[3-13].However,most of them were constructed under conventional public key cryptography (PKC) and thus inevitably suffers from the cumbersome certificate problem.To solve this issue,Abdallaet al.[14] introduced searchable encryption into identity-based cryptography (IBC) [15] and brought forth the notion of identity-based encryption with keyword search (IBEKS).Compared with PEKS,IBEKS has the merit of no certificate.In [14],Abdallaet al.provided the definition of IBEKS,together with a general construction of IBEKS from anonymous hierarchical identity-based encryption.Since then,several IBEKS schemes have been proposed [16-22].In addition,searchable encryption was also introduced into attribute-based encryption so as to extend IBEKS by associating ciphertexts and trapdoors with sets of descriptive attributes [23-26].However,the user private keys in IBEKS are issued by a completely trusted private key generator,which leads to the key escrow problem.

In order to address the problems imposed on the previous searchable PKE schemes,Penget al.[27] proposed certificateless encryption with keyword search (CLEKS) that follows the idea of certificateless public key cryptography (CLPKC) presented by Al-Riyamiet al.[28].The concept of CLPKC lies between conventional PKC and IBC.When using CLPKC,a user should first apply for a partial private key from a trusted third party called key generation center (KGC).Then,he/she randomly picks a secret value and produces his/her full private key by combining the secret value with the partial private key.The user public key is also calculated by using the secret value.Because the user private key is unknown to the KGC,CLPKC avoids the key escrow problem inherently in IBC while preserving the certificateless property.In [27],Penget al.first put forward a CLEKS scheme with a designated server.Later,Zhenget al.[29] presented another CLEKS scheme but without a designated server.Recently,Maet al.[30,31] respectively presented a CLEKS scheme and a designated server CLEKS scheme.

Motivations and contributions.In [32,33],Byunet al.and Yauet al.respectively observed the keyword guessing (KG) attacks on some PEKS schemes.By performing the KG attack,an attacker (an outside attacker or a malicious inside storage server) may reveal the keyword from a keyword ciphertext or a keyword trapdoor.This attack exploits the low-entropy property of the commonly-used keywords.Because the users often select some keywords from a small keyword space (such as the English words from an English dictionary) to generate their encrypted data,the attacker may successfully guess the keywords encoded in the users’ encrypted data and trapdoors in an exhaustive manner.As introduced in [32],the latest edition of Merriam-Webster’s collegiate dictionary includes approximately 225000 entries.Thus,the probability to guess a keyword correctly in a brute force way is about 1/218.For another example,the current Oxford English Dictionary contains approximately 600000 entries and thus the probability is about 1/219to guess a correct keyword.Actually,this probability will be higher if the attack applies to some particular application,e.g.email application,which has much smaller keyword space containing commonly-used keywords such as {urgent,high,normal,low,…}.Undoubtedly,the KG attack has become the most devastating attack on the keyword search encryption schemes,since it may lead to the disclosure of the information pertaining to the encrypted data.Till now,many PEKS schemes have been demonstrated to be insecure under the KG attack [32-35].

In this paper,we demonstrate that the CLEKS frameworks introduced in [27,29] are inherently vulnerable to the KG attack.By presenting concrete attacks,we show that both CLEKS with a designated server [27] and CLEKS without a designated server [29] suffer from either the inside offline KG attack or the outside online KG attack.The security vulnerability of these two CLEKS frameworks lies in the fact that anyone can compute the ciphertext of any keyword by the target receiver’s public key.Thus,an outside attacker or a malicious inside storage server is able to prepare the ciphertexts of all possible keywords and then run the testing algorithm or use the server as a testing oracle to reveal the keyword in a given trapdoor.Our attacks imply that it is impossible to build a CLEKS scheme resisting KG attacks under the previously proposed frameworks.Therefore,how to devise a secure CLEKS scheme is still an unsolved problem.

To fight against KG attacks,we put forward a new framework for CLEKS.The presented framework remedies the inherent security weakness in the previous CLEKS frameworks [27,29] and provides resistance to both the inside and outside KG attacks.Under the new framework,we construct a concrete CLEKS scheme.In the random oracle model [36],the proposed scheme is formally proved to achieve the ciphertext indistinguishability under the bilinear Diffie-Hellman (BDH) assumption and the trapdoor indistinguishability under the hash Diffie-Hellman (HDH) assumption.Compared with the previous CLEKS schemes [27,29-31],our CLEKS scheme has better overall performance and offers stronger security guarantee as it can withstand the existing known types of keyword guessing attacks.

Paper organization.In Section 2,we briefly review the notion of bilinear pairing and two computational assumptions.In Section 3,we present the KG attacks on the previous CLEKS frameworks.In Section 4,we define a new framework for CLEKS and the corresponding security notions.The proposed CLEKS scheme is described and analyzed in Section 5.Finally,we give our conclusions in Section 6.

II.BILINEAR PAIRING AND COMPUTATIONAL ASSUMPTIONS

Assuming thatqis a big prime number and (G1,G2) are two cyclic groups of same orderq.A mape:G1×G1→G2is called a bilinear pairing if it satisfies the following attributes:

- Bilinearity:For anyU,V∈G1andx,y∈Zq,e(xU,yV) =e(U,V)xy;

- Non-degeneracy:There existU,V∈G1such thate(U,V)≠1;

- Computability:For anyU,V∈G1,there exists an efficient algorithm to calculatee(U,V).

Our CLEKS scheme is proven secure under the bilinear Diffie-Hellman (BDH) assumption [37] and the hash Diffie-Hellman (HDH) assumption [38].

Definition 1.Given a tuple (P,xP,yP,zP)∈(G1)4for unknown valuesx,y,z∈Zq,the BDH problem in (G1,G2) is to computee(P,P)xyz∈G2.The advantage of an algorithmABDHin solving the BDH problem is defined to be

Adv(ABDH) = Pr[ABDH(P,xP,yP,zP) =e(P,P)xyz|P∈G1∧x,y,z∈Zq].

The BDH assumption states that the advantageAdv(ABDH) is negligible for any algorithmABDH.

Definition 2.LetH:G1→{0,1}lbe a hash function,wherelis an integer denoting the length of the hash value.Given the hash functionHand a tuple (P,xP,yP,Z)∈(G1)3×{0,1}lfor unknownx,y∈Zq,the HDH problem inG1is to decide whetherZ=H(xyP).The advantage of an algorithmAHDHin solving the HDH problem is defined to be

Adv(AHDH) = |Pr[AHDH(H,P,xP,yP,H(xyP)) = 1 |P∈G1∧x,y∈Zq]

- Pr[AHDH(H,P,xP,yP,H(zP)) = 1 |P∈G1∧x,y,z∈Zq]|.

The HDH assumption states that the advantageAdv(AHDH) is negligible for any algorithmAHDH.

III.CRYPTANALYSIS OF PREVIOUS CLEKS FRAMEWORKS

3.1 Description of previous CLEKS frameworks

So far,two different CLEKS frameworks have been proposed in the literature.They are CLEKS with a designated server [27] and CLEKS without a designated server [29].

A CLEKS scheme with a designated server is composed of eight algorithms [27]:

- Setup:On input a security parameterl,this algorithm produces the KGC’s master secret keymkand a set of public system parameterspp.

- Extract-Partial-Private-Key:On input the set of public system parameterspp,the KGC’s master secret keymkand an entityE’s identityIDE,this algorithm produces a partial private keyPSKEfor the entityE,where the entityEis either a designated server or a user.

- Set-Secret-Value:On input the set of public system parametersppand an entityE’s identityIDE,this algorithm produces a secret valuesvEfor the entityE.

- Set-Private-Key:On input the set of public system parameterspp,an entityE’s identityIDE,secret valuesvEand partial private keyPSKE,this algorithm produces a private keySKEfor the entityE.

- Set-Public-Key:On input the set of public system parameterspp,an entityE’s identityIDEand secret valuesvE,this algorithm produces a public keyPKEfor the entityE.

- Encrypt:On input the set of public system parameterspp,a keywordw,a designated serverS’s identityIDSand public keyPKSand a receiverR’s identityIDRand public keyPKR,this algorithm produces a keyword ciphertextCw.

- Trapdoor:On input the set of public system parameterspp,a keywordw,a designated serverS’s public keyPKSand a receiverR’s private keySKR,this algorithm produces a keyword trapdoorTw.

- Test:On input the set of public system parameterspp,a keyword ciphertextCw,a keyword trapdoorTw′and a designated serverS’s private keySKS,this algorithm outputs 1 meaning thatCwandTw′correspond to the same keyword (i.e.,ww= ′) or 0 otherwise.

The framework of CLEKS without a designated server [29] is almost as same as that of CLEKS with a designated server,except that the algorithmsEncrypt,TrapdoorandTestdo not require the input of a designated server’s public/private key.

3.2 Types of adversaries and KG attacks

Two types of adversaries are involved in our presented KG attacks.They are the outside attacker and the malicious inside server:

-Outside attacker:This adversary is able to eavesdrop on the public channel and then obtain the ciphertexts and the trapdoors that are transmitted over the public channel.However,it cannot perform the algorithmTestagainst the CLEKS scheme with a designated server,because the algorithm Test needs a designated server’s private key as input.

-Malicious inside server:This adversary can receive the encrypted data and the keyword ciphertexts from a sender.It can also receive the keyword trapdoors from a receiver.Most importantly,it is able to execute the algorithmTestto verify whether a keyword ciphertext matches with a given keyword trapdoor.Therefore,compared with the outside attacker,the malicious inside server has the stronger attack ability.

Till now,three types of KG attacks have been introduced in the literature:

-Offline outside KG attack[32]:In this attack,once capturing a trapdoor from a target receiver,the outside attacker generates the ciphertexts of all possible keywords by using the target receiver’s public key and then verifies whether his guess is correct by matching these ciphertexts with the trapdoor in an offline manner.

-Online outside KG attack[39]:This attack was proposed by Yauet al.[39] against the security of PEKS with a designated server.In this attack,the outside attacker simulates a sender by sending some false encrypted data that are associated with the candidate keywords to the designated serverand then makes use of the latter as a testing oracle to verify its guess.This attack is feasible as it only requires the outside attacker to eavesdrop the communication between the designated server and the target receiver without compromising either the server or the receiver.

-Offline inside KG attack[32]:In this attack,the malicious inside server traverses the keyword space to guess the keyword encoded in a keyword trapdoor in an offline manner since it has the ability to execute both the algorithmsEncryptandTest.After guessing a correct keyword,it can further determine which encrypted data contains the keyword.

3.3 Cryptanalysis of CLEKS with a designated server

In a CLEKS scheme with a designated server,the keyword is encrypted by using both the designated server’s and the receiver’s public keys.Thus,only the designated server is able to perform the algorithm Test to verify whether a keyword ciphertext matches a given keyword trapdoor by using its private key.Therefore,the CLEKS scheme with a designated server resists the offline outside KG attack.However,it suffers from the online outside KG attack.Concretely,an outside attacker can perform an online outside KG attack on a CLEKS scheme with a designated server as follows:

- Step 1:Guess all possible keywords {w1,w2,…,wn} and then perform the algorithmEncryptto calculate the ciphertexts of these keywords {C1,C2,…,Cn} by using the designated serverS’s public keyPKSand the target receiverR’s public keyPKR.

- Step 2:Fake the encrypted data {Enc(data1),Enc(data2),…,Enc(datan)} corresponding to the keywords {w1,w2,…,wn} by using the target receiverR’s public keyPKRand then simulate a sender by sendingEnc(data1)||C1,Enc(data2)||C2,…,Enc(datan)||Cnto the receiverR.Note that the encrypted dataEnc(-data1)||C1,Enc(data2)||C2,…,Enc(datan)||Cnwill be transmitted to the designated serverS.

- Step 3:When receiving a trapdoorTwfrom the receiverR,the designated serverSreturns all matching encrypted data (including the one corresponding to the correct keyword guess as previously sent by the outsider attacker) to the receiverRbased on the testing result.

- Step 4:Recall that a CLEKS scheme with a designated server does not assume a secure communication channel.Therefore,the outside attacker can wiretap the communication channel between the serverSand the receiverR.It knows which trapdoor has been sent by the receiver.Upon observing the encrypted data including one of its crafted encrypted data (i.e.implying a correct guess) that is verifiable by it (e.g.Enc(datai) in the scenario above),it is able to determine that the embedded keyword iswi.

In the above attack,although the outside attacker cannot run thealgorithmTest,it can still make use of the designated server as a testing oracle to get the testing results.This attack can be avoided if a secure channel is established between the designated server and each receiver.Even so,a CLEKS scheme with a designated server is still vulnerable to the offline inside KG attack.Concretely,a malicious inside server can perform an offline inside KG attack as follows:

-Step 1:Receive a keyword trapdoorTwfrom any receiverR;

-Step 2:Guess a candidate keywordw*and then execute the algorithmEncryptto calculate the ciphertextCw*of the keywordw*by using its public keyPKSand the receiverR’s public keyPKR.

-Step 3:Execute the algorithmTestto verify whetherTwmatches withCw*.If it does,thenw*is a correct keyword.Else,go to Step 2 and repeat.

By the above attack,a malicious inside server can successfully disclose the keyword in a given keyword trapdoor.What’s worse is that after guessing a correct keyword,the malicious inside server can further execute the algorithmTestto determine which encrypted data contains the keyword.

3.4 Cryptanalysis of CLEKS without a designated server

In a CLEKS scheme without a designated server,the keyword is encrypted under the receiver’s public key and anyone is able to perform the algorithmTestto verify whether a keyword ciphertext matches with a given keyword trapdoor.Therefore,the keyword trapdoors must be sent to the storage server via secure channels.If not,an outside attacker can intercept the trapdoors from the public channel and then perform the offline outside KG attack to disclose the keywords encoded in these trapdoors.However,even if the keyword trapdoors are transmitted secretly,a CLEKS scheme without a designated server is still vulnerable to the offline inside KG attack.Concretely,a malicious inside server can attack the scheme through the following steps:

-Step 1:Receive a keyword trapdoorTwfrom any receiverR;

-Step 2:Guess a candidate keywordw*and then perform the algorithmEncryptto calculate the ciphertextCw*of the keywordw*by using its public keyPKSand the receiverR’s public keyPKR;

-Step 3:Perform the algorithmTestto verify whetherTwmatches withCw*.If it does,thenw*is a correct keyword.Else,go to Step 2 and repeat.

Similarly,after guessing a correct keyword,the malicious server can further execute the algorithmTestto determine which encrypted data contains the keyword.

IV.NEW FRAMEWORK AND SECURITY MODEL OF CLEKS

4.1 Design idea of the new framework

As shown by the attacks presented in the above section,the main reason that the previous CLEKS frameworks suffer from either the online outside KG attack or the offline inside KG attack is that the keyword ciphertext is calculated under the designated server’s and the receiver’s public keys (in CLEKS with a designated server [27]) or the receiver’s public key (in CLEKS without a designated server [29]).Therefore,an attacker (either a malicious designated server or an outside attacker) has the ability to generate the ciphertext of any keyword for any receiver.By guessing all possible keywords and generating the ciphertexts of these candidates,the attacker is able to run the algorithmTest(in the case of offline inside KG attack) or use the designated server as a testing oracle (in the case of online outside KG attack) to reveal the keyword in a given trapdoor.

To fight against the KG attack,our CLEKS framework embeds the sender’s private key into the calculation of keyword ciphertexts so that a keyword ciphertext can be generated correctly only by both the sender’s private key and the receiver’s public key.Because the sender’s private key is unknown to anyone except the sender,it prevents the attackers (including the outside attackers and the malicious inside servers) from running the keyword encryption algorithmEncryptto generate a valid ciphertext of any keyword.Without the ability to generate the ciphertexts of the keywords it guesses,the attacker cannot launch a successful KG attack anymore.In this way,our new framework provides resistance against both the outside KG attack and the inside KG attack.

4.2 Framework definition

As illustrated in figure 1,the proposed CLEKS framework involves four different entities,namely:a KGC,a storage server,a sender and a receiver.The KGC controls the generation of the master secret key and the public system parameters.It is also responsible for producing a partial private key for the sender and the receiver.The sender produces the data ciphertexts and the corresponding keyword ciphertexts,and sends them to the storage server.The receiver is able to retrieve the data ciphertexts sent to him/her on the storage server.To do so,the receiver should first send the storage server a trapdoor of the search keyword.When receiving a keyword trapdoor from the receiver,the storage server searches the encrypted data for the receiver by using the keyword trapdoor and then returns all matching encrypted data.

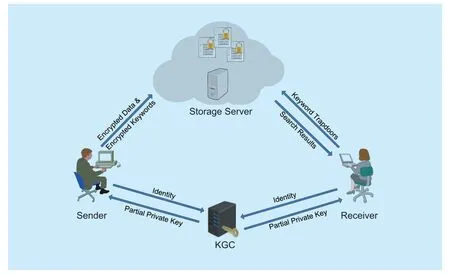
Fig.1.System model of the proposed CLEKS framework.

Formally,the proposed CLEKS framework is composed of the following six algorithms:

-Setup(l):On input a security parameterl,this algorithm produces the KGC’s master secret keymkand a set of public system parameterspp.

-Extract-Partial-Private-Key(pp,mk,IDU):On input the set of public system parameterspp,the KGC’s master secret keymkand a userU’s identityIDU,this algorithm produces a partial private keyPSKUfor the userU.

-Set-User-Key(pp,IDU,PSKU):On input the set of public system parameterspp,a userU’s identityIDUand partial private keyPSKU,this algorithm produces a private keySKUand a public keyPKUfor the userU.Specially,a senderS’s private/public key pair is denoted by (SKS,PKS),while a receiverR’s private/public key pair is denoted by (SKR,PKR).

-Encrypt(pp,w,IDS,SKS,IDR,PKR):On input the set of public system parameterspp,a keywordw,a senderS’s identityIDSand private keySKSand a receiverR’s identityIDRand public keyPKR,this algorithm produces a keyword ciphertextCw.

-Trapdoor(pp,w,IDS,PKS,IDR,SKR):On input the set of public system parameterspp,a keywordw,a senderS’s identityIDSand public keyPKSand a receiverR’s identityIDRand private keySKR,this algorithm produces a keyword trapdoorTw.

-Test(pp,Cw,Tw′):On input the set of public system parameterspp,a keyword ciphertextCwand a keyword trapdoorTw′,this algorithm outputs 1 meaning thatCwandTw′correspond to the same keyword (i.e.,ww= ′) or 0 otherwise.

Definition 3.A CLEKS scheme is correct if for any keywordw,Cw=Encrypt(pp,w,IDS,SKS,IDR,PKR) andTw′=Trapdoor(pp,w,IDS,PKS,IDR,SKR),thenTest(pp,Cw,Tw′) = 1,wherepp,(SKS,PKS) and (SKR,PKR) are respectively generated according to the specification of the algorithmSetup,the algorithmExtract-Partial-Private-Keyandthe algorithmSet-User-Key.

4.3 Security model

As introduced in [27,29],two distinct adversaries should be considered in the security model of CLEKS,namely the Type 1 adversary and the Type 2 adversary.The Type 1 adversary models a malicious inside server or an outside attacker who cannot access the KGC’s master secret keymk,but is able to replace public keys.The Type 2 adversary models an honest-but-curious KGC in possession of the KGC’s master secret key who can produce a partial private key for any user,but is disallowed to replace public keys.

To formalize the security model,we first define seven oracles.A Type 1 (or Type 2) adversary can query some of these oracles adaptively.These oracles are controlled by a challenger and responded as follows:

-OCreateUser:On input a user’s identityIDU,a public keyPKUis responded ifIDUhas already been created.Else,the identityIDUis created by producing a private/public key pair (SKU,PKU) and thenPKUis returned.We assume that the following six oracles merely respond to a user’s identityIDUthat has been created.

-OPrivateKey:On input a user’s identityIDU,a private keySKUis responded.

-OPartialPrivateKey:On input a user’s identityIDU,a partial private keyPSKUis responded.

-OReplaceKey:On input a user’s identityIDUand a false public keyPKUf,the current public key associated with the identityIDis replaced byHere,the adversary is asked to supply the corresponding private keySKUf.This restriction is imposed due to the fact that the challenger may not know the corresponding private key if a user’s public key has been replaced.This oracle is merely queried by the Type 1 adversary.

-OEncrypt:On input a keywordw,a senderS’s identityIDSand a receiverR’s identityIDR,a keyword ciphertextCwis responded.

-OTrapdoor:On input a keywordw,a senderS’s identityIDSand a receiverR’s identityIDR,a keyword trapdoorTwis responded.

-OTest:On input a keyword ciphertextCwand a keyword trapdoorTw′,this oracle outputs 1 meaning thatCwandTw′correspond to a same keyword or 0 otherwise.This oracle models the ability of an adversary to run the algorithmTestor make use of the server as a testing oracle.

A CLEKS scheme must achieve ciphertext indistinguishability under the adaptive chosen-keyword attack (hereafter referred to as “CT-IND-CKA security”),which guarantees that an adversary cannot distinguish the ciphertexts of two different keywords on which they want to be challenged.This security notion can be defined by the following adversarial gameCT-IND-CKA-Gamethat is played between a challenger and a Type 1/Type 2 adversaryA.

(1)Setup.The challenger simulates the algorithmSetup(l) to produce the KGC’s master secret keymkand a set of public system parameterspp.Then,it provides the adversaryAwithppif it is a Type 1 adversary or bothppandmkif it is a Type 2 adversary.

(2)Phase 1.During the query-answer phase,the adversaryAadaptively queries the oracles {OCreateUser,OPrivateKey,OPartialPrivateKey,OReplaceKey,OEncrypt,OTrapdoor,OTest} if it is a Type 1 adversary or the oracles {OCreateUser,OPrivateKey,OEncrypt,OTrap-door,OTest} if it is a Type 2 adversary.

(3)Challenge.The adversaryAoutputs a senderS’s identityIDS,a receiverR’s identityIDRand two different keywords (w0,w1).The challenger randomly selects a bitb∈{0,1} and calculatesCwb=Encrypt(pp,wb,IDS,SKS,IDR,PKR) as a challenge keyword ciphertext.Then,it returnsCwbto the adversaryA.

(4)Phase 2.As in Phase 1,the adversaryAcontinues to make a sequence of oracle queries.

(5)Guess.Eventually,the adversaryAgives its guessb′∈{0,1}.It wins ifb=b′ and the following conditions are simultaneously satisfied:

- The adversaryAhas never queried the oracleOTrapdooron either (IDS,IDR,w0) or (IDS,IDR,w1);

- The adversaryAhas never queried the oraclesOPrivateKeyandOPartialPrivateKeyon eitherIDSorIDRif it is a Type 1 adversary;

- The adversaryAhas never queried the oracleOPrivateKeyon eitherIDSorIDRif it is a Type 2 adversary.

The advantage of the adversaryAin winning the above game is defined to be 2|Pr[b=b′] - 1/2|.

Definition 4.A CLEKS scheme satisfies the CT-IND-CKA security if no PPT adversary has a non-negligible advantage in the above game.

To prove a CLEKS scheme to be secure against KG attacks,we next define the security of trapdoor indistinguishability under the KG attack (hereafter referred to as “TD-INDKGA security”).The TD-IND-KGA security guarantees that a Type 1/Type 2 adversary who has obtained the trapdoor of the challenge keyword under the challenge identities is unable to determine the relation between the trapdoor and the challenge keyword.This security notion can be defined by the following adversarial gameTD-IND-KGA-Gamethat is played between a challenger and a Type 1/Type 2 adversaryA.

(1)Setup.The challenger simulates the algorithmSetup(l) to produce the KGC’s master secret keymkand a set of public system parameterspp.Then,it provides the adversaryAwithppif it is a Type 1 adversary or bothppandmkif it is a Type 2 adversary.

(2)Phase 1.During the query-answer phase,the adversaryAadaptively queries the oracles {OCreateUser,OPrivateKey,OPartialPrivateKey,OReplaceKey,OEncrypt,OTrapdoor,OTest} if it is a Type 1 adversary or the oracles {OCreateUser,OPrivateKey,OEncrypt,OTrap-door,OTest} if it is a Type 2 adversary.

(3)Challenge.The adversaryAoutputs a senderS’s identityIDS,a receiverR’s identityIDRand two different keywords (w0,w1).The challenger randomly selects a bitb∈{0,1} and calculatesTwb=Trapdoor(pp,wb,IDS,PKS,IDR,SKR).Then,it returnsTwbas a challenge keyword trapdoor to the adversaryA.

(4)Phase 2.As in Phase 1,the adversaryAcontinues to make a sequence of oracle queries.

(5)Guess.Eventually,the adversaryAgives its guessb′∈{0,1}.It wins ifb=b′ and the following conditions are simultaneously satisfied:

- The adversaryAhas never queried the oracleOEncrypton either (IDS,IDR,w0) or (IDS,IDR,w1);

- The adversaryAhas never queried both the oraclesOPrivateKeyandOPartialPrivateKeyon eitherIDSorIDRif it is a Type 1 adversary;

- The adversaryAhas never queried the oracleOPrivateKeyon eitherIDSorIDRif it is a Type 2 adversary.

The advantage of the adversaryAin winning the above game is defined to be 2|Pr[b=b′] - 1/2|.

Definition 5.A CLEKS scheme satisfies the TD-IND-KGA security if no PPT adversary has a non-negligible advantage in the above game.

V.A NEW CLEKS SCHEME

5.1 Description of the scheme

The proposed CLEKS scheme is described as follows:

-Setup(l):On input a security parameterl,this algorithm produces two cyclic groups (G1,G2) of samel-bit prime orderqand a bilinear mape:G1×G1→G2.It then randomly selects a generatorP∈Gand an integers∈Zq,computesPpub=sP.Assuming thatH0:{0,1}*→G1,H1:G2→{0,1}l,H2:G1→{0,1}l,H3:G2→{0,1}landH4:{0,1}*×{0,1}l×{0,1}l→Zqare five hash functions,wherel∈Z+is the bit-length of the hash value.Finally,this algorithm returns the KGC’s master secret keymk=sand a set of public system parameterspp= {q,G1,G2,e,P,Ppub,H0,H1,H2,H3,H4}.

-PartialKeyGen(pp,mk,IDU):On input the set of system public parameterpp,the KGC’s master secret keymk=sand a userU’s identityIDU,this algorithm computes a partial private keyPSKU=sQUfor the userU,whereQU=H0(IDU).

-UserKeyGen(pp,IDU,PSKU):On input the set of public system parameterpp,a userU’s identityIDUand partial private keyPSKU=sQU,this algorithm randomly choosesxU∈Zq,sets the user’s private keySKU= (SKU1,SKU2) = (xU,sQU) and computes the corresponding public keyPKU=xUP.

-Encrypt(pp,w,IDS,SKS,IDR,PKR):On input the set of public system parameterpp,a keywordw,a senderS’s identityIDSand private keySKS= (SKS1,SKS2) and a receiverR’s identityIDRand public keyPKR,this algorithm randomly choosesr∈Zqand computes the keyword ciphertextwhereQR=H0(IDR),st1=H2(SKS1PKR) andst2=H3(e(SKS2,QR)).

-Trapdoor(pp,w′,IDS,PKS,IDR,SKR):On input the set of public system parameterpp,a keywordw′,a senderS’s identityIDSand public keyPKSand a receiverR’s identityIDRand private keySKR= (SKR1,SKR2),this algorithm computes the keyword trapdoorTw′=H4(w′,st1′,st2′)(SKR1QR+SKR2),whereQS=H0(IDS),QR=H0(IDR),st1′=H2(SKR1PKS) andst2′=H3(e(QS,SKR2)).

-Test(pp,Cw,Tw′):On input the set of public system parameterpp,a keyword ciphertextCw= (Cw1,Cw2) and a keyword trapdoorTw′,this algorithm checks whetherCw2=H1(e(Cw1,Tw′)) holds.It outputs 1 if it does or 0 otherwise.

5.2 Correctness of the scheme

Theorem 1.Our CLEKS scheme is correct.

Proof.According to the description of the proposed CLEKS scheme,we have

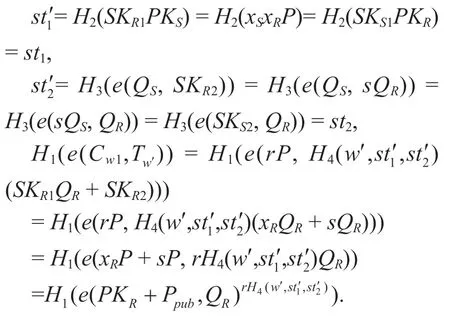
Obviously,ifw=w′,thenCw2=H1(e(Cw1,Tw′)).

Therefore,the proposed CLEKS scheme is correct.

5.3 Security proof

Theorem 2.Our CLEKS scheme achieves the CT-IND-CKA security under the BDH assumption in the random oracle model.

We prove this theorem by the following two lemmas.

Lemma 1.LetH0～H4be five random oracles.If there exists a Type 1 adversaryA1who has a non-negligible advantageeagainst the CT-IND-CKA security of our CLEKS scheme,then there must be an algorithmABDHwho has a non-negligible advantageε′ ≥ (ε/q1qCU)(1-1/qCU)qTto solve theBDH problem,whereq1,qCUandqTrespectively denote the maximal number of the adversaryA1’s queries toH1,OCreateUserandOTrapdoor.

Proof.Let (P,aP,bP,cP) be a BDH problem instance given to the algorithmABDH.To computee(P,P)abc,the algorithmABDHsimulates a CT-IND-CKA-Game challenger and interacts with the adversaryA1as follows:

Setup.The algorithmABDHfirst setsPpub=aP.It then randomly selects an indexq∈{1,2,…,qCU} and provides the adversaryA1with the set of public system parameterspp= {q,G1,G2,e,P,Ppub,H0,H1,H2,H3,H4},whereH0～H4are five random oracles.

Phase 1andPhase 2.During two query-answer phases,the adversaryA1can query the oracles {H0,H1,H2,H3,H4,OCreateUser,OPrivateKey,OPartialPrivateKey,OReplaceKey,OEncrypt,OTrapdoor,OTest} in an adaptive manner.The algorithmABDHanswers the adversaryA1’s various queries in the following way:

-H0queries:To answer these queries,the algorithmABDHkeeps a listH0-Listthat is composed of the tuples (IDi,Qi,h0i).On receiving an identityIDi,the algorithmABDHperforms as follows:(1) If the identityIDihas been contained in a tuple (IDi,Qi,h0i) on the listH0-List,it outputsQidirectly; (2) Else ifIDi=IDθ(i.e.,IDiis theq-th distinct identity submitted to the oracleOCreateUser),it setsQθ=bP,inserts a new tuple (IDθ,Qθ,⊥) intoH0-Listand outputsQθ; (3) Otherwise,it randomly choosesh0i∈Zq,setsQi=h0iP,inserts a new tuple (IDi,Qi,h0i) intoH0-Listand outputsQi.

-H1queries:To answer these queries,the algorithmABDHkeeps a listH1-Listthat is composed of the tuples (Ti,h1i).On receiving a valueTi∈G2,the algorithmABDHperforms as follows:(1) If the valueTihas been contained in a tuple (Ti,h1i) on the listH1-List,it outputsh1idirectly; (2) Otherwise,it randomly choosesh1i∈{0,1}l,adds a new tuple (Ti,h1i) toH1-Listand outputsh1i.

-H2queries:To answer these queries,the algorithmABDHkeeps a listH2-Listthat is composed of the tuples (mi,h2i).On receiving a valuemi∈G1,the algorithmABDHperforms as follows:(1) If the valuemihas been contained in a tuple (mi,h2i) on the listH2-List,it outputsh2idirectly; (2) Otherwise,it randomly choosesh2i∈{0,1}l,adds a new tuple (mi,h2i) toH2-Listand outputsh2i.

-H3queries:To answer these queries,the algorithm ABDHkeeps a listH3-Listthat is composed of the tuples (ni,h3i).On receiving a valueni∈G2,the algorithm ABDHperforms as follows:(1) If the valuenihas been contained in a tuple (ni,h3i) on the listH3-List,it outputsh3idirectly; (2) Otherwise,it randomly choosesh3i∈{0,1}l,adds a new tuple (ni,h3i) toH3-Listand outputsh3i.

-H4queries:To answer these queries,the algorithmABDHkeeps a listH4-Listthat is composed of the tuples (wi,st1i,st2i,h4i).On receiving (wi,st1i,st2i),the algorithmABDHperforms as follows:(1) If (wi,st1i,st2i) has been contained in a tuple (wi,st1i,st2i,h4i) on the listH4-List,it outputsh4idirectly; (2) Otherwise,it randomly choosesh4i∈Zq,adds a new tuple (wi,st1i,st2i,h4i) toH4-Listand outputsh4i.

-OCreateUserqueries:To answer these queries,the algorithmABDHkeeps a listUser-Listthat is composed of the tuples (IDi,PKi,SKi).On receiving an identityIDi,the algorithmABDHperforms as follows:(1) If the identityIDihas been contained in a tuple (IDi,PKi,SKi) on the listUser-List,it outputsPKidirectly; (2) Else ifIDi=IDθ(namely thatIDiis theq-th distinct identity submitted to this oracle),it randomly choosesxθ∈Zq,setsPKθ=xθPandSKθ= (xθ,⊥),adds a new tuple (IDθ,PKθ,SKθ) toUser-Listand then outputsPKθ; (3) Otherwise,it randomly choosesxi∈Zq,simulates a queryH0(IDi)to obtainh0i,setsPKi=xiPandSKi= (xi,h0i(aP)),adds a new tuple (IDi,PKi,SKi) toUser-Listand outputsPKi.

-OPrivateKeyqueries:When receiving an identityIDi,the algorithmABDHaborts ifIDi=IDθ.Otherwise,it searchesIDiin the listUser-Listto find a tuple (IDi,PKi,SKi) and outputsSKi.

-OPartialPrivateKeyqueries:When receiving an identityIDi,the algorithmABDHaborts ifIDi=IDθ.Otherwise,it searchesIDiin the listUser-Listto find a tuple (IDi,PKi,SKi) and outputsSKi2.

-OReplaceKeyqueries:When receiving an identityIDiand a false public keyPKif,the algorithmABDHrecords the replacement.Note that the adversaryA1needs to supply the secret value used to produce the false public keyPKif.

-OEncryptqueries:When receiving a keywordw,a sender’s identityIDiand a receiver’s identityIDj,the algorithmABDHrespectively searches the identitiesIDiandIDjin the listsUser-ListandH0-Listto find tuples (IDi,PKi,SKi),(IDj,PKj,SKj) and (IDj,Qj,h0j).Then,it randomly choosesr∈Zqand calculatesCw= (Cw1,Cw2) = (rP,H1(e(PKj+Ppub,H4(w,st1,st2)Qj)r)),wherest1=H2(SKi1PKj) andst2=H3(e(aP,h0j(bP))) ifidi=iDθorH3(e(SKi2,Qj)) otherwise.Finally,it outputsCw.

-OTrapdoorqueries:When receiving a keywordw,a sender’s identityIDiand a receiver’s identityIDj,the algorithmABDHaborts ifidj=iDθ.Otherwise,it respectively searches the identitiesIDiandIDjin the listsUser-ListandH0-Listto find tuples (IDi,PKi,SKi),(IDj,PKj,SKj) and (IDj,Qj,h0j).Then,it computesTw=H4(w,st1,st2)(SKj1Qj+SKj2),wherest1=H2(SKj1PKi) andst2=H3(e(aP,h0j(bP))) ifidi=iDθorH3(e(SKi2,Qj)) otherwise.Finally,it outputsTw.

-OTestqueries:On receiving a keyword ciphertextCw= (Cw1,Cw2) and a keyword trapdoorTw′,the algorithmABDHoutputs 1 if the equationCw2=H1(e(Cw1,Tw′)) holds or 0 otherwise.

Challenge.In this phase,the adversaryA1outputs its challenge (IDS,IDR,w0,w1).IfIDR≠IDθ,then the algorithmABDHaborts.Else,it randomly selectsb∈{0,1},produces a challenge keyword ciphertextand outputsCwβ,wheregis randomly selected from {0,1}l.Note thatCwβ2is implicitly defined asH1(e(PKθ+Ppub,H4(wb,st1*,st2*)Qθ)c),wherest1*=H2(SKS1PKθ) andst2*=H3(e(SKi2,Qθ)).

Guess.Eventually,the adversaryA1outputs its guess that is ignored by the algorithmABDH.To solve the given BDH problem,the algorithmABDHrandomly selects a tuple (Ti,h1i) from the listH1-Listand then calculates

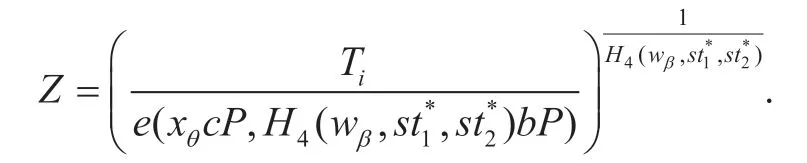
Recall that we havePpub=aPandQθ=bP.Thus,ifTi=e(PKθ+Ppub,H4(wb,st1*,st2*)Qθ)c,then we can easily deduce thatZ=e(P,P)abc.Therefore,the valueZis a correct answer to the BDH problem.

Next,we derive the bound on the advantage of the algorithmABDH.LetAbortdenote the event that the algorithmABDHabnormally aborts during the game andQueryH1denote the event that the adversaryA1makes a queryH1(e(PKθ+Ppub,H3(wb,st)Qθ)c) respectively.According to the above simulation,the eventAbortoccurs only when one of the following events occurs:

-E1:In the challenge phase,the adversaryA1does not chooseIDθas the target receiver’s identity;

-E2:The adversaryA1queries the oracleOPrivateKeyonIDθ;

-E3:The adversaryA1queries the oracleOPartialPrivateKeyonIDθ;

-E4:The adversaryA1submits the identityIDθas a receiver’s identity to the oracle OTrapdoor;

We clearly have that Pr[¬E1] = 1/qCU,Pr[¬E4] =(1 - 1/qCU)qTand the event ¬E1implies both the events ¬E2and ¬E3.Thus,Pr[¬Abort] = Pr[¬E1∧¬E2∧¬E3∧¬E4] ≥(1/qCU)(1- 1 /qCU)qT.

LetE*=QueryH1|¬Abort.Clearly,if the eventE*does not occur,then the adversaryA1cannot gain an advantage greater than 1/2 in guessingb.Therefore,Pr[β=β′|¬E*] = 1/2.By splitting Pr[β=β′],we get Pr[β=β′] = Pr[β=β′|¬E*]×Pr[¬E*] + Pr[β=β′|E*]×Pr[E*]≤Pr[¬E*]/2 + Pr[E*] = 1/2 +Pr[E*]/2.According to the definition of the adversary’s advantage in the game CTIND-CKA-Game,we havee≤Pr[E*]≤Pr[QueryH1]/Pr[¬Abort].Hence,Pr[QueryH1]≥e× Pr[¬Abort].

Because once the eventQueryH1happens,the algorithmABDHcan computee(P,P)abcby selecting the correct tuple fromH1-Listwith probability 1/q1.Therefore,we get the algorithmABDH’s advantage

ε′≥Pr[QueryH1]/q1≥(ε/q1qCU)(1- 1/qCU)qT.

This completes the proof of Lemma 1.#

Lemma 2.LetH0～H4be five random oracles.If there exists a Type 2 adversaryA2who has a non-negligible advantageeagainst the CT-IND-CKA security of our CLEKS scheme,then there must be an algorithmABDHwho has a non-negligible advantageε′ ≥ (ε/q1qCU)(1-1/qCU)qTto solve theBDH problem,whereq1,qCUandqTrespectively denote the maximal number of the adversaryA2’s queries toH1,OCreateUserandOTrapdoor.

Proof.Let (P,aP,bP,cP) be a BDH problem instance given to the algorithmABDH.To computee(P,P)abc,the algorithmABDHsimulates a CT-IND-CKA-Game challenger and interacts with the adversaryA2as follows:

Setup.The algorithmABDHfirst randomly selectssZ∈q*and calculatesPpub=sP.It then randomly selects an indexq∈{1,2,…,qCU} and provides the adversaryA2with the set of public system parameterspp= {q,G1,G2,e,P,Ppub,H0,H1,H2,H3,H4} and the master secret keymk=s,whereH0～H4are five random oracles.

Phase 1andPhase 2.During two query-answer phases,the adversaryA2can query the oracles {H0,H1,H2,H3,H4,OCreateUser,OPrivateKey,OEncrypt,OTrapdoor,OTest} in an adaptive manner.The algorithmABDHanswers the queries toH0,H1,H2,H3,H4,OPrivateKeyandOTestas in the proof of Lemma 1 and handles other queries as follows:

-OCreateUserqueries:To answer these queries,the algorithmABDHkeeps a listUser-Listthat is composed of the tuples (IDi,PKi,SKi).On receiving an identityIDi,the algorithmABDHperforms as follows:(1) If the identityIDihas been contained in a tuple (IDi,PKi,SKi) on the listUser-List,it outputsPKidirectly; (2) Else ifIDi=IDθ(namely thatIDiis theq-th distinct identity submitted to this oracle),it setsPKθ=aPandSKθ= (⊥,sbP),adds a new tuple (IDθ,PKθ,SKθ) to the listUser-Listand outputsPKθ; (3) Otherwise,it randomly choosesxi∈Zq,simulates a queryH0(IDi)to obtainh0i,setsPKi=xiPandSKi= (xi,h0i(sP)),adds a new tuple (IDi,PKi,SKi) to the listUser-Listand outputsPKi.

-OEncryptqueries:On receiving a keywordw,a sender’s identityIDiand a receiver’s identityIDj,the algorithmABDHrespectively searches the identitiesIDiandIDjin the listsUser-ListandH0-Listto find tuples (IDi,PKi,SKi),(IDj,PKj,SKj) and (IDj,Qj,h0j).Then,it randomly selectsr∈Zqand calculatesCw= (Cw1,Cw2) = (rP,H1(e(PKj+Ppub,H4(w,st1,st2)Qj)r)),wherest2=H3(e(SKi2,Qj)) andst1=H2(SKj1aP) ifIDi=IDθorH2(SKi1aP) ifIDj=IDθ.Finally,it outputsCw.

-OTrapdoorqueries:When receiving a keywordw,a sender’s identityIDiand a receiver’s identityIDj,the algorithmABDHaborts ifidj=iDθ.Otherwise,it respectively searches the identitiesIDiandIDjin the listsUser-ListandH0-Listto find tuples (IDi,PKi,SKi),(IDj,PKj,SKj) and (IDj,Qj,h0j).Then,it computesTw=H4(w,st1,st2)(SKj1Qj+SKj2),wherest1=H2(SKj1PKi) andst2=H3(e(SKi2,Qj)).Finally,it outputsTw.

Challenge.In this phase,the adversaryA2outputs its challenge (IDS,IDR,w0,w1).IfIDR≠IDθ,then the algorithmABDHaborts.Else,it randomly selectsb∈{0,1},produces a challenge keyword ciphertextCwβ=(Cwβ1,Cwβ2) =(cP,γ) and outputsCwβto the adversaryA2,wheregis selected from {0,1}lrandomly.Note thatCwβ2is implicitly defined asH1(e(PKθ+Ppub,wherest1*=H2(SKS1PKθ) andst2*=H3(e(SKS2,Qθ)).

Guess.Eventually,the adversaryA2outputs its guess that is ignored by the algorithmABDH.To solve the given BDH problem,the algorithmABDHrandomly selects a tuple (Ti,h1i) from the listH1-Listand then calculates

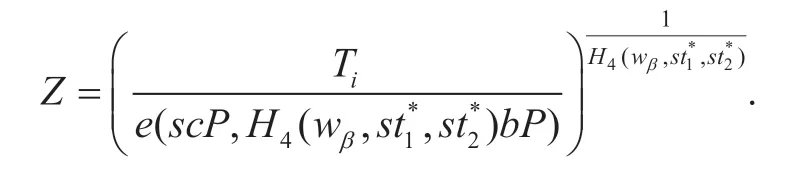
Recall that we havePpub=sP,PKθ=aPandQθ=bP.Thus,ifTi=e(PKθ+Ppub,H4(wb,st1*,st2*)Qθ)c,then we can easily deduce thatZ=e(P,P)abc.Therefore,the valueZis a correct answer to the BDH problem.As in the proof of Lemma 1,we can deduce that the algorithmABDH’s advantage is bounded byε′ ≥ (ε/q1qCU)(1-1/qCU)qT.

This completes the proof of Lemma 2.#

Theorem 2.Our CLEKS scheme achieves the TD-IND-KGA security under the HDH assumption in the random oracle model.Concretely,suppose that there exists a Type 1/Type 2 adversaryAwho has a non-negligible advantageeagainst the TD-IND-CKA security of our CLEKS scheme,then there must be an algorithmAHDHwho has a non-negligible advantageε′ ≥ε/qCU(qCU-1) to solve theHDH problem,whereqCUis the maximal number ofA’s queries toOCreateUser.

Proof.Let (H2,P,aP,bP,Z) be a HDH problem instance given to the algorithmAHDH.To decide whetherZ=H2(abP),the algorithmAHDHsimulates a CT-IND-KGA-Game challenger and interacts with the adversaryAas follows:

Setup.The algorithmAHDHfirst randomly selectss∈Zqand calculatesPpub=sP.It then randomly selects two random indicesI,J∈{1,2,…,qCU} and provides the adversaryAwith the set of public system parameterspp= {q,G1,G2,e,P,Ppub,H0,H1,H2,H3,H4},whereH0～H4are five random oracles.The adversaryAis also given the master secret keymk=sif it is a Type 2 adversary.

Phase 1andPhase 2.During two query-answer phases,the adversaryAis able to query the oracles {H0,H1,H2,H3,H4,OCreateUser,OPri-vateKey,OPartialPrivateKey,OReplaceKey,OEncrypt,OTrapdoor,OTest} if it is a Type 1 adversary or the oracles {H0,H1,H2,H3,H4,OCreateUser,OPrivateKey,OEncrypt,OTrapdoor,OTest} if it is a Type 2 adversary.The algorithmAHDHanswers the queries toH1,H3,H4,OReplaceKeyandOTestas in the proof of Lemma 1 and handles other oracle queries in the following way:

-H0queries:To answer these queries,the algorithmAHDHkeeps a listH0-Listthat is composed of the tuples (IDi,Qi,h0i).When receiving an identityIDi,the algorithmAHDHperforms as follows:(1) If the identityIDihas been contained in a tuple (IDi,Qi,h0i) on the listH0-List,it outputsQidirectly; (2) Otherwise,it randomly choosesh0i∈Zq,setsQi=h0iP,adds a new tuple (IDi,Qi,h0i) toH0-Listand outputsQi.

-H2queries:To answer these queries,the algorithmAHDHkeeps a listH2-Listthat is composed of the tuples (mi,h2i).When receiving a valuemi∈G1,the algorithmAHDHperforms as follows:(1) If the valuemihas been contained in a tuple (mi,h2i) on the listH2-List,it outputsh2idirectly; (2) Else ife(mi,P) =e(aP,bP),it adds a new tuple (mi,Z) to the listH2-Listand outputsZ; (3) Otherwise,it randomly choosesh2i∈{0,1}l,adds a new tuple (mi,h2i) toH2-Listand outputsh2i.

-OCreateUserqueries:To answer these queries,the algorithmAHDHkeeps a listUser-Listthat is composed of tuples (IDi,PKi,SKi).When receiving an identityIDi,the algorithmAHDHperforms as follows:(1) If the identityIDihas been contained in a tuple (IDi,PKi,SKi) on the listUser-List,it outputsPKidirectly; (2) Else ifIDi=IDI(namely thatIDiis theI-th distinct identity submitted to this oracle),it setsPKI=aPandSKI= (⊥,sQI),adds a new tuple (IDI,PKI,SKI) to the listUser-Listand outputsPKI; (3) Else ifIDi=IDJ(namely thatIDiis theJ-th distinct identity submitted to this oracle),it setsPKJ=bPandSKJ= (⊥,sQJ),adds a new tuple (IDJ,PKJ,SKJ) to the listUser-Listand outputsPKJ; (4) Otherwise,it randomly choosesxi∈Zq,setsPKi=xiPandSKi= (xi,sQi),adds a new tuple (IDi,PKi,SKi) to the listUser-Listand outputsPKi.

-OPrivateKeyqueries:When receiving an identityIDi,the algorithmAHDHaborts ifIDi=IDIorIDi=IDJ.Otherwise,it searchesIDiin the listUser-Listto find a tuple (IDi,PKi,SKi) and outputsSKi.

-OPartialPrivateKeyqueries:When receiving an identityIDi,the algorithmAHDHaborts ifIDi=IDIorIDi=IDJ.Otherwise,it searchesIDiinthe listUser-Listto find a tuple (IDi,PKi,SKi) and outputsSKi2.

Table I.Different cases during the simulation of the OEncryptoracle.

Table II.Different cases during the simulation of the OTrapdoororacle.

-OEncryptqueries:When receiving a keywordw,a sender’s identityIDiand a receiver’s identityIDj,the algorithmAHDHfirst randomly selectsr∈Zq,searches the identitiesIDiandIDjin the listsUser-ListandH0-Listto find tuples (IDi,PKi,SKi),(IDj,PKj,SKj) and (IDj,Qj,h0j).It then responds with a keyword ciphertext as shown in Table 1.

-OTrapdoorqueries:When receiving a keywordw,a sender’s identityIDiand a receiver’s identityIDj,the algorithmABDHfirst respectively searchesIDiandIDjin the lists

User-ListandH0-Listto find tuples (IDi,PKi,SKi),(IDj,PKj,SKj),(IDi,Qi,h0i) and (IDj,Qj,h0j).It then responds as shown in Table 2.

Challenge.In this phase,the adversaryAoutputs its challenge (IDS,IDR,w0,w1).If ¬(IDS=IDI∧IDR=IDJ) and ¬(IDS=IDJ∧IDR=IDI),then the algorithmAHDHaborts.Clearly,the probability that the game is not aborted abnormally isElse,it randomly choosesb∈{0,1},searchesIDRin the listsUser-ListandH0-Listto find tuples (IDR,PKR,SKR) and (IDR,QR,h0R) and then does the following:(1) IfIDS=IDIandIDR=IDJ,it setsTwβ= H4(wb,st1*,st2*)(h0JbP+sQJ),wherest1*=Zandst2*=H3(e(QI,sQJ)); (2) Else ifIDS=IDJandIDR=IDI,it setsTwβ= H4(wb,st1*,st2*)(h0IaP+sQI),wherest1*=Zandst2*=H3(e(QJ,sQI)).

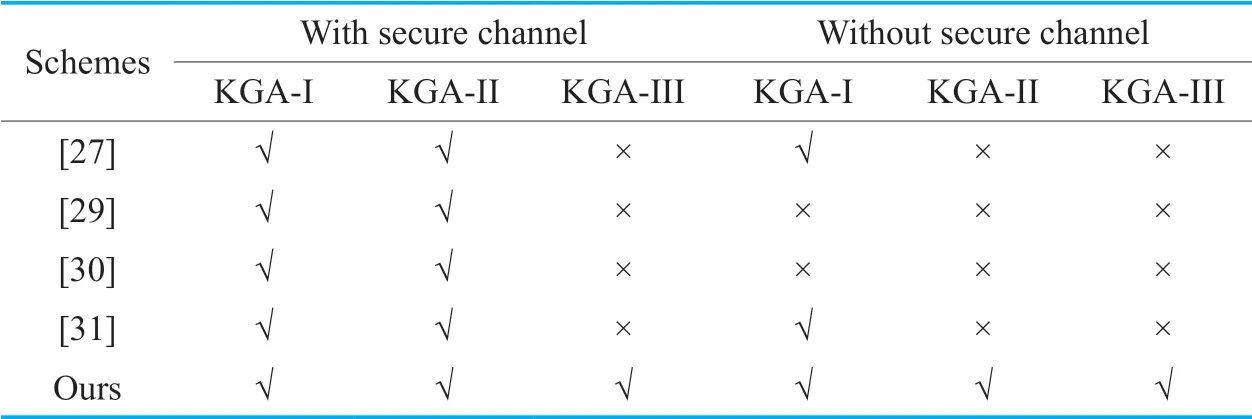
Table III.Security of the compared schemes.

Table IV.Notations in the performance comparison.

Guess.Eventually,the adversaryAoutputs a guessβ′.Ifββ′= ,then the algorithmAHDHoutputs 1 meaning thatZ=H2(abP) or 0 otherwise.

Next,we derive the algorithmAHDH’s advantage.LetAbortdenote the event thatAHDHaborts abnormally during the game.Then,we have Pr[¬Abort] = Pr[(IDS=IDI∧IDR=IDJ)∨(IDS=IDJ∧IDR=IDI)].Because the adversaryAmakes at mostqCUqueries to the oracleOCreateUser,the probabilityPr[¬Abort] is at leastIn addition,if the eventAbortdoes not occur,then 2|Pr[ββ= ′] - 1/2| =e(namely that Pr[ββ= ′] = 1/2 ±e/2) ifZ=H2(abP) or Pr[ββ= ′] = 1/2 otherwise.Therefore,the algorithmAHDHcan solve the given HDH problem with a non-negligible advantage

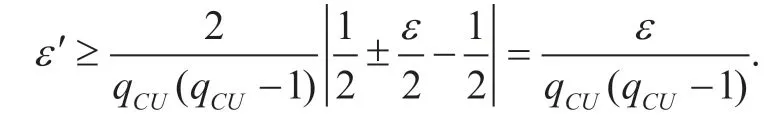
This completes the proof of Theorem 2.#

5.4 Performance analysis

To evaluate the performance of our CLEKS scheme,we compare it with the previous two CLEKS schemes [27,29-31].The details of the compared CLEKS schemes are shown in Table 3 and Table 5,where KGA-I,KGAII and KGA-III respectively denote whether the scheme can resist the offline outside KG attack,the online outside KG attack and the offline inside KG attack.

As listed in Table 4,five basic cryptographic operations are considered in the comparison.As usual,the costs of general cryptographic hash,point addition inG1and modular addition inZqare ignored.The cost of an algorithm is measured by the sum of the costs of all cryptographic operations.For example,to encrypt a keywordw,the encryption algorithm in our CLEKS scheme requires computing two bilinear pairing,one exponentiation in the groupG2,three scalar multiplications inG1and one map-to-point hash.Therefore,the cost of the algorithm is 2TP+ TE+ 3TM+ TMH.In addition,the size of the public system parameters/user public key/ciphertext/trapdoor is measured in terms of the total number of the group elements and hash values.For example,a keyword ciphertext in our scheme is composed of oneelement inG1and a hash value.Thus,its size is (|G1|+l) bits.

To give a more intuitive comparison,we estimate the running time of the compared CLEKS schemes on a laptop running Windows 7 (64bit) with Intel (R) CoreTMi7 CPU@2.3GHz and 8GB RAM memory.The benchmark time of different operations and the bit-length of different elements are shown in Table 6.We get the benchmark time of different operations using the PBC (Pairing-Based Cryptography) library [40].To obtain the security level of 1024-bit RSA,we use the Type A pairing defined over the supersingular elliptic curveE(Fq):y2= x3+ xwith embedding degree 2,where the group sizeqis a 512-bit prime satisfyingq+ 1 =prandpis a 160-bit Solinas prime.For the parameterspandr,we use the values (r= 120160122648911460793 8882136674053420480295440125131182291 9615131047207 28935970453110284480218 3906537786776 andp= 7307508186654516 213611192455715049014059 76559617) recommended by PBC.In addition,we use SHA-1 as the general cryptographic hash function.Hence,the lengthlof a hash valueis 160 bits.The experimental results are given in Table 7.

We can see that our CBSE scheme outperforms the CLEKS scheme proposed by Zhenget al.[29] in both the computation and communication costs.Compared with the CLEKS schemes [27,30,31],our scheme is less efficient in the keyword trapdoor generation algorithm.But,it enjoys obvious advantage in both the keyword encryption algorithm and the testing algorithm.For the communication cost,our scheme is as efficient as the one in [31] and is better than the ones in [27,30].Most importantly,as shown by Table 3,our scheme resists the existing known three types of KG attacks,while other CLEKS schemes[27,29-31] do not.

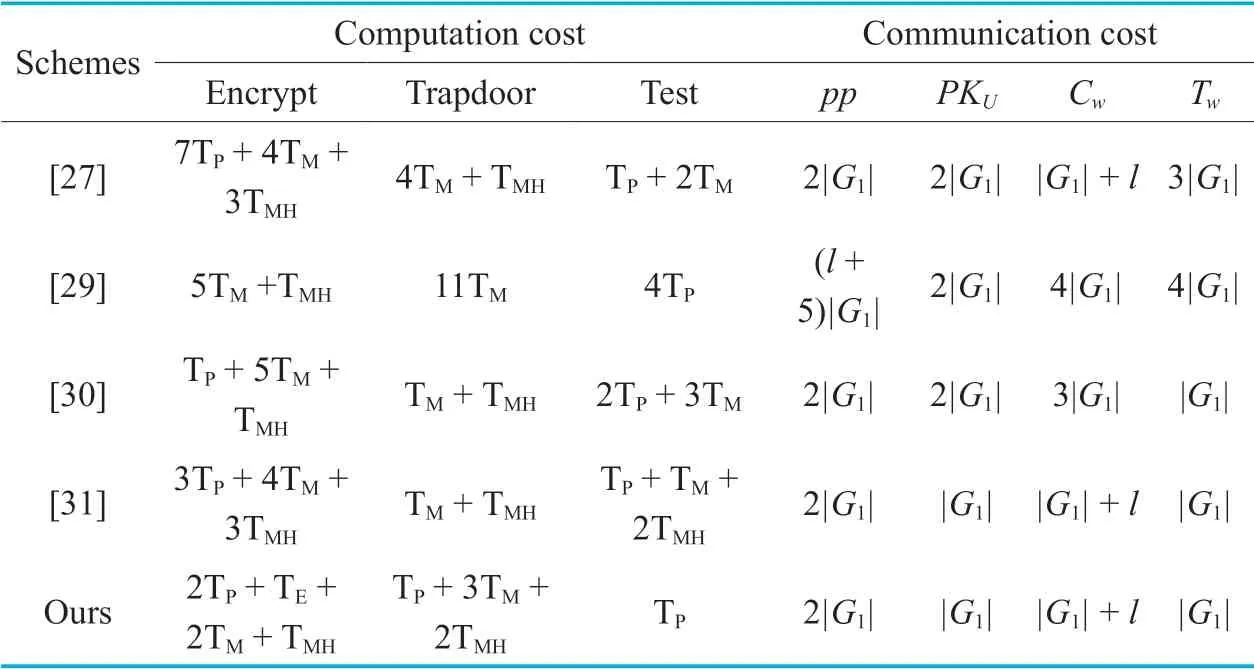
Table V.Computation and communication cost of the compared CLEKS schemes.

Table VI.Benchmark time of different operations and bit-length of different elements.

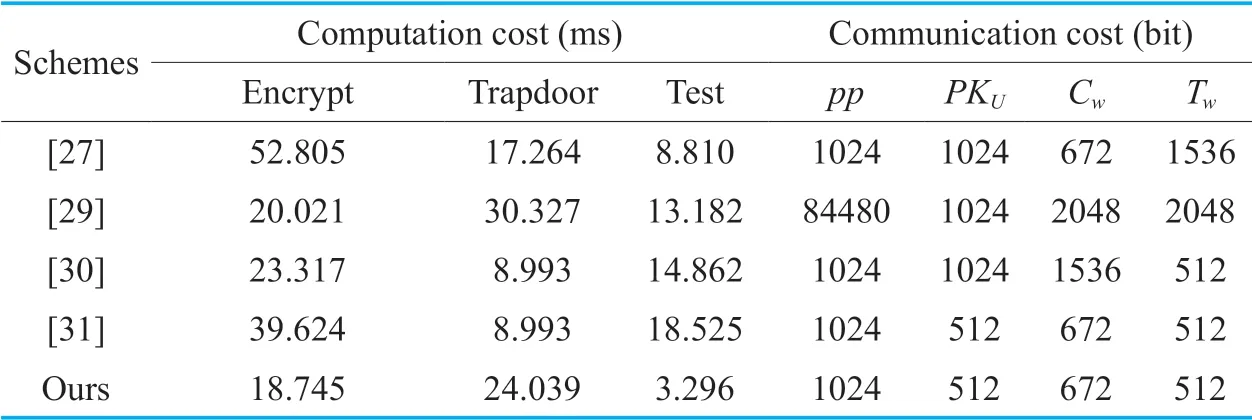
Table VII.Experimental results of the compared CLEKS schemes.

VI.CONCLUSIONS

In this paper,we have demonstrated that the previous frameworks of CLEKS are inherently vulnerable to the KG attack.To solve this problem,we have proposed a new framework for CLEKS schemes.Our new framework remedies the security vulnerability in the previous CLEKS frameworks and provides resistance to both the outside KG attack and the inside KG attack.Under the new framework,we have designed a concrete CLEKS scheme and proven its security under the BDH and HDH assumptions in the random oracle model.In comparison to the previously proposed CLEKS schemes,it has better overall performance and offers stronger security guarantee under the KG attacks.

To fight against KG attacks,our CLEKS framework needs to embed the sender’s private key in each keyword ciphertext,namely that it generates the keyword ciphertext by using the sender’s private key and the receiver’s public key.Accordingly,the receiver should involve the sender’s public key in the generation of the keyword trapdoors.This implies that our CLEKS framework provides limited search function,since the receiver needs to designate the sender when he/she wants to search on his/her received ciphertexts.It may be inefficient when the ciphertexts are from multiple senders.So,it would be more interesting to devise a CLEKS framework that is immune to the KG attack while offering full search function (namely that a receiver is able to locate all ciphertexts that contain a specific keyword by a single keyword trapdoor,regardless of who sends him/her the ciphertexts).This is a more challenging work.We leave it as our future work and also pose it as an open problem.

ACKNOWLEDGEMENTS

This work is supported by the National Natural Science Foundation of China under Grant Nos.61772009 and U1736112,the Natural Science Foundation of Jiangsu Province under Grant Nos.BK20161511 and BK20181304.