Low-Complexity Joint Channel Estimation and Symbol Detection for OFDMA Systems

Rui Xin,Zuyao Ni＊,Sheng Wu,Linling KuangChunxiao Jiang

1 Department of Aerospace Engineering,Tsinghua University,Beijing 100084,China

2 Tsinghua Space Center,Tsinghua University,Beijing 100084,China

3 Key Laboratory of Universal Wireless Communication,Ministry of Education,Beijing University of Posts and Telecommunications,Beijing 100876,China

4 Beijing National Research Center for Information Science and Technology,Beijing 100084,China

Abstract: In this paper,we propose a joint channel estimation and symbol detection (JCESD) algorithm relying on message-passing algorithms (MPA) for orthogonal frequency division multiple access (OFDMA) systems.The channel estimation and symbol detection leverage the framework of expectation propagation (EP) and belief propagation (BP) with the aid of Gaussian approximation,respectively.Furthermore,to reduce the computation complexity involved in channel estimation,the matrix inversion is transformed into a series of diagonal matrix inversions through the Sherman-Morrison formula.Simulation experiments show that the proposed algorithm can reduce the pilot overhead by about 50%,compared with the traditional linear minimum mean square error (LMMSE) algorithm,and can approach to the bit error rate (BER) performance bound of perfectly known channel state information within 0.1 dB.

Keywords: joint channel estimation and symbol detection; message passing; OFDMA

I.INTRODUCTION

Recently,the development of mobile intelligent terminal and mobile Internet has brought about an explosive growth of data services,and proposed challenging requirements in rate and capacity for 5G wireless communications [1],[2].Owing to its flexible resource allocation,high spectrum efficiency and anti-multipath interference capability,orthogonal frequency division multiple access (OFDMA) technology has been widely adopted in modern communication systems,such as LTE-A/LTE [3],[4],and also a powerful candidate for 5G wireless communication systems [5]-[7].Having accurate channel estimate in OFDMA systems is essential,as it affects both the detection performance of uplink and the precoding performance of the downlink significantly.However,traditional pilot-based channel estimation algorithms require a large number of pilot overhead,which is usually proportional to the number of channel impulse response (CIR) taps.Moreover,sophisticated channel estimation algorithms,such as linear minimum mean square error (LMMSE),have prohibitively high complexity due to matrix inversions,which requires a complexity as high as the cube of the number of subcarriers.The number of channel taps ranges from tens to hundreds,and the number of subcarriers ranges from several thousand to tens of thousands,resulting in very high overhead and complexity.Therefore,designing a low-complexity and low-overhead channel estimation method for OFDMA systems is a great challenge and has attracted extensive research interests in the past few years.

Many researchers have made great efforts to improve the performance and reduce the complexity of the OFDMA channel estimation algorithm [8]-[18].A hybrid of linear and basic extended model (BEM) interpolation method was proposed in [8],which can improve the performance of time-frequency least squares (LS) interpolation channel estimation.Yang et al.in [9] proposed a windowed discrete Fourier transform (DFT) based on minimum mean square error (MMSE) estimator to suppress the noise interference,which performs weighted-vector filter by selecting a frequency-domain Hanning window.Given the irregular pilot allocation of the OFDMA uplink,subspace-tracking is considered in [10] to obtain the correlation matrix of channel estimation instead of the averaging in [17].In OFDMA systems,channel estimation is only based on a subset of pilot subcarriers,resulting in performance degradation.To this end,papers [8]-[13] proposed channel estimation algorithms based on maximum likelihood (ML) [19],subspace [20] or expectation maximization (EM) [21] methods to eliminate the loss caused by partial subcarriers.However,algorithms in [8]-[13] all suffered from a high computational complexity,and the sacrifice of complexity can only lead to a slight performance improvement over the MMSE.For low complexity,a simplified MMSE algorithm relying on an approximate matrix inversion was proposed in [14] and [15].In particular,these channel estimation methods in [8]-[15] suffered from a large pilot overhead when the number of channel multipath taps are large.To solve this problem,a channel estimation algorithm that superimposes training symbols onto transmitted data symbols was proposed in [16],where the pilot symbols do not need to occupy additional subcarriers and reduce a lot of overhead.However,the superposition of data symbols and pilot symbols results in unsatisfactory channel estimation performance,and a high complexity is cost to reduce the interference iteratively by superimposed training.Factor graph and the sum-product algorithm (SPA) [22] provide a framework for iterative joint channel estimation and symbol detection,which can improve estimation accuracy and BER performance with low pilot overhead.However,it is implausible to use standard sum product algorithm on a factor graph for joint channel estimation and symbol detection due to an exponential complexity.To obtain a feasible algorithm,different message passing algorithms (MPA),such as the BP algorithm,EM algorithm and particle filter algorithm,are proposed in [23]-[25].Recently,the MPA has been proposed for the decoding of sparse code multiple access (SCMA) [26] in 5G wireless networks,which can bring an improvement in system capacity.Moreover,the MPA was also used in the joint channel estimation and detection for MIMO-OFDM system [27],where the performance of channel estimation is improved by taking the transforming relation of the time-domain channel and the frequency-domain channel into account.In this paper,we propose a joint iterative channel estimation and symbol detection algorithm using message passing algorithm for OFDMA systems,which can effectively improve the channel estimation accuracy,BER performance,and reduce pilot overhead.Specifically,we transform the matrix inversion into a recursive representation of the diagonal matrix inversion through the Sherman-Morrison formula [28],which helps the complexity of the matrix inversion drop fromtowhere the number of zero-tapsLsis much smaller than the number of subcarriersKnallocated to the user.Extensive simulations show that the proposed algorithm can achieve the oracle bound of perfect channel state information within 0.1 dB.Compared with the traditional MMSE algorithm,the proposed algorithm can reduce the pilot overhead by about 50% and reduce complexity simultaneously.

Notation:The transpose operation and the conjugate transpose operation is denoted by superscript T and H,respectively.Idenotes an identity matrix.Also,denotes a Gaussian function whose mean ismand variance isv;xxidenotes the symbols inxwithxiexcluded.δ(⋅) is the Kronecker delta function.Furthermore,D(x) constructs a diagonal matrix from the vectorrepresents the message passed from thefnode to thexnode in the thiiteration.

II.SYSTEM MODEL

We consider an OFDMA system usingKsubcarriers and servingNactive single-antenna users.Subcarriers are indexed by{k} ,k=1…K,where subcarrier set {n1,… ,nKn} is assigned to usernandUsers occupy different subcarriers to communicate with the base station (BS).

For the transmitter of usern,the binary information bitsbnare encoded and interleaved to form the coded bitscn.Then each Q bits incnare mapped into constellation set A to form a modulation symbol,where A satisfiesFor channel estimation,pilot symbolsxnpare mixed with generated data symbolsxnd,sequentially placed in the allocatedKnsubcarriers for usern,while other subcarriers do not send symbols.The set of pilot-subcarriers belong to usernis represented by P={(t,k) :xtkis a pilot symbol} ,and the set of data-subcarriers is denoted by D = {(t,k) :k=n1,… ,nKn∩P} [27].The frequency-domain symbols in thetth OFDM symbols are denoted byand then are modulated to an OFDM symbol by aK-point FFT based modulation.To eliminate intersymbol interference (ISI),a cyclic prefix (CP) has been added as the guard interval before the OFDM symbol is transmitted.

In a frequency-selective channel,the CIR between the user and the BS is denoted byh=[h1,… ,hL]T,wherehlis thelth time-domain tap coefficient andLis the number of multipath taps.We assume that the wireless channel is time-varying but keep static within one OFDM symbol.The frequency channel coefficient at thekth subcarrier of thetth OFDM symbol is given by

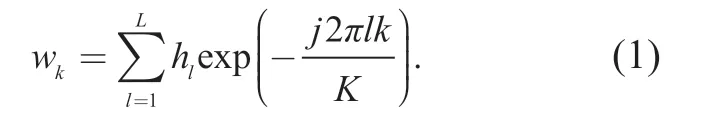
At the receiver,received signalytin frequency-domain is obtained by aK-point discrete Fourier transform (DFT) based demodulation after removing CP,which can be written as

whereyt=[yt1,… ,ytK]T,w=diag [w1,… ,wK],andϖ=[ϖ1,… ,ϖK]T.Then the frequency domain received symbol at thekth subcarrier of thetth OFDM symbolytkreads

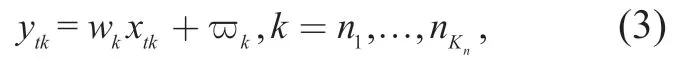
whereϖkdenotes a Gaussian white noise with zero mean and varianceσϖ2.

III.FACTOR GRAPH REPRESENTATION

At the receiver of the base station,the data symbols at subcarrier set {n1,… ,nKn} are extracted to estimate channel state information (CSI) and decode to obtain information bits.We need to accurately estimate the information bit sequencebnand the frequency domain channel tap coefficientsfrom the received signal ytand the known pilot sequencesxnp.To achieve the lowest bit error rate,the maximum aposterioriprobability (MAP) estimation is employed,i.e.,

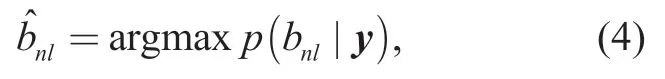
wherebnldenote thelth information bit inbn,and the aposterioriprobability is obtained by

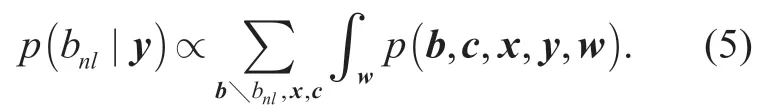
The joint probability in (5) can be factored into

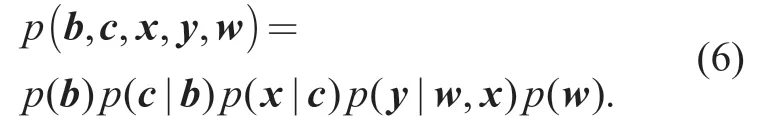
Due to the fact that the symbols on different subcarriers are independent,the conditional probabilityp(|)xcin (6) can be expressed asthe channel transition functionp(|,)ywxcan be factorized intowhereFinally,φ(ctk) represents a symbol mapping function.

As shown in figure 1,the probabilistic structure of the system can be represented by a factor graph [29],[30],where the symbol mapping function node Mtkrepresents theδ(φ(xtk-ctk)) constraint,and the nodeftkrepresents channel transfer function.We choose to pass the message from right to left first and then update the resulting message from left to right.The full cycle of message passing is considered as a “turbo iteration”.

IV.MESSAGE PASSING FOR JOINT CHANNEL ESTIMATION AND SYMBOL DETECTION

In this section,we propose a joint iterative channel estimation and symbol detection algorithm for OFDMA systems with the aid of message passing algorithm and Gaussian approximate.EP is used in channel estimation and BP with Gaussian approximate (BP-GA) is used in symbol detection.

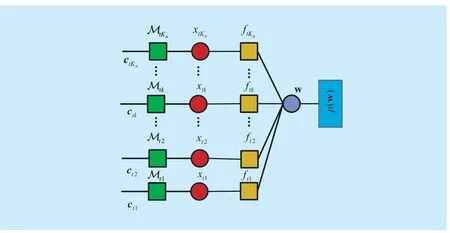
Fig.1.Factor graph of the JCESD for OFDMA systems.

4.1 Channel estimation

In this subsection,we consider the channel estimation part for OFDMA systems.At the start of the turbo iteration,only poilts are used for initial channel estimation to obtain CSI,and then we use the output of the decoder to form a data-aided channel estimation.

In figure 1,we start from the aprioriprobability of the variable nodew,where the apriorimean and covariance matrix are given by

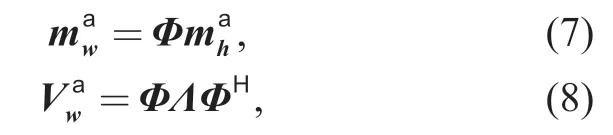
The local belief ofwkis defined by [29],[31]

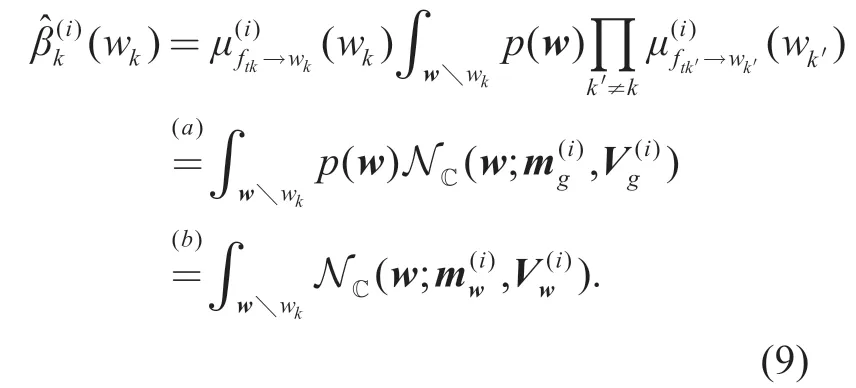
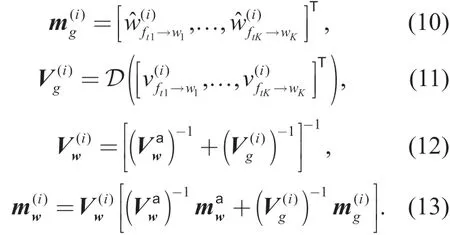
Finally,we also need to obtain the messagefrom the variable nodewkto the function nodeftk.According to the expectation propagation algorithm,we can getand its mean and covariance as follows [27],

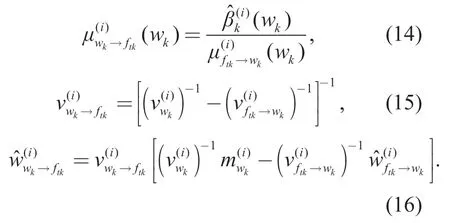
4.2 Symbol detection

In this subsection,we consider the symbol detection part of our algorithm.We get more and more accurate data through iterative symbol detection,which can improve the accuracy of channel estimation.

In the function nodeftk,we consider the channel transfer function in theith turbo iteration as

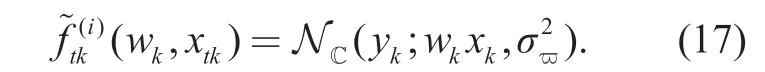
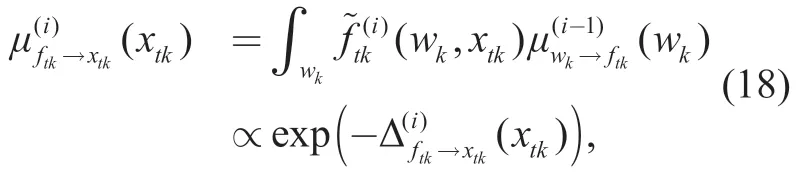
where

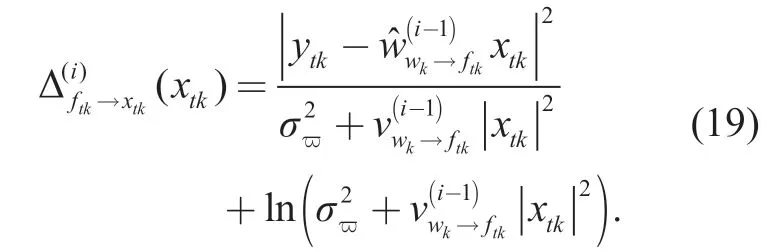
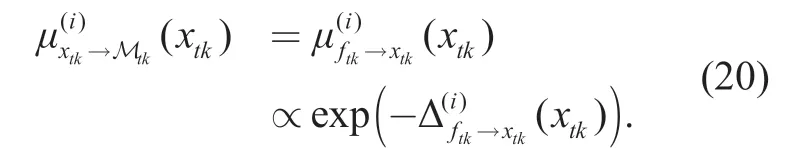
We input the extrinsic informationobtained from the previous iteration into the decoder as the aprioriinformation in theith iteration.The decoder output the extrinsic log-likelihood ratio[33]

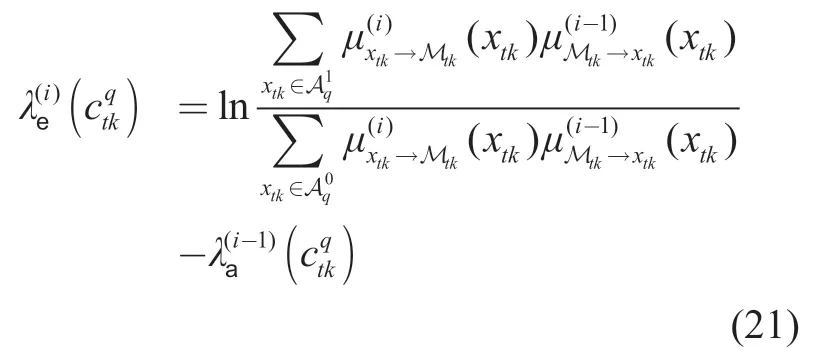
where the message updating from the mapping node Mtkto the variable nodextkis given by

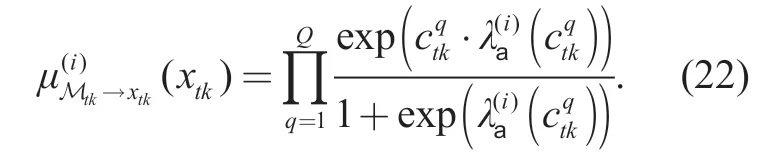
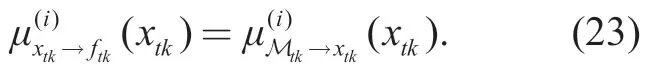
By calculation we can obtain the mean and variance of thextknode

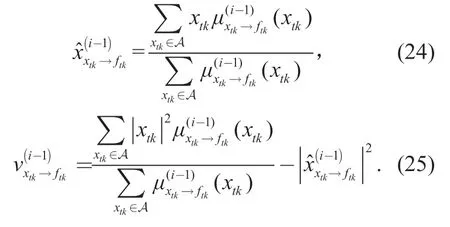
For a known pilot symbolxtk∈P,the messagecan be easily obtained by

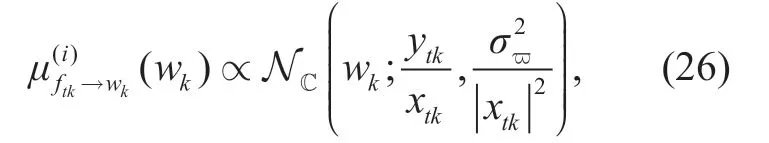
We use this information to perform initial channel estimation as mentioned above.

However,for an unknown data symbolxtk∈D,the expression of messageis more involved,as it is a mixture of Gaussian functions as given by

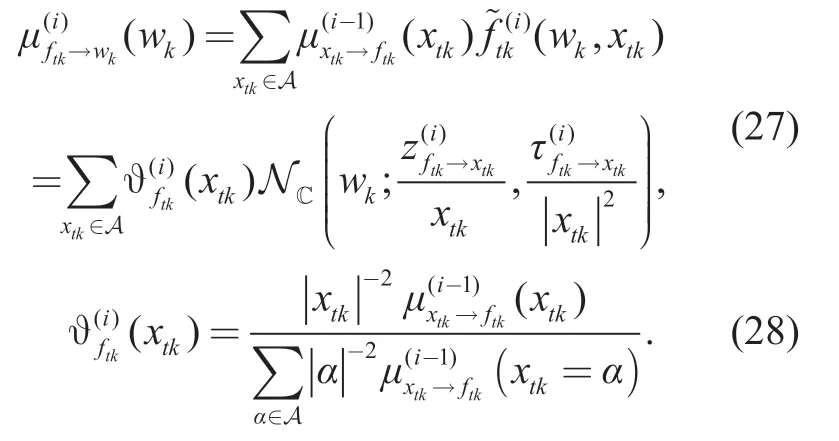
To avoid the explosion of Gaussian components,we can project the messageinto a Gaussian function[34]

Table I.The BP-GA in symbol detection part at the ith turbo iteration.Input:∀ ∈(tk x ν w ν σ,:,.(0) (0) (0) (0)) D ˆ ˆ,,,,x f x f w f w f→→→→ ϖ ytk tk tk tk k tk k tk(0) (0)Initialization:i tk x ν=∀ ∈ = =1 ,0,1,,:( ) Dˆx f x f→→tk tk tk tk(0) (0) (0) w ν qλ cq ˆw f w f tk →==∀ =0,1,and :0.→k tk k tk a( )For (tk,)∈Dx( 1)-2 ()µi-→tk x f tk-2i( ) ,;xxϑf tk tktk tk =(xtkx∀ ∈α∑∈Aα µ α( 1)i-→x f tk tk tk( )= ) Ai 1)Δ =()f x tkitk tk→ ( )x-ˆy w xtk w f tk( -1k tk 2(i-→ )2 2σ ν ln ,ϖ+w f tk →k tk (2(i 1σ νx )x xϖ+ + ∀ ∈w f tk tk-→k tk 2) A()i x∑tk∈Ai ϑf tk→= ∀∈w y x( )x ,;A ˆ()f w tk tktktk k xtk() () 2 ()f w tk f w tki ν σ 2)x∑ϑf tk tk ( )x 2ˆ2,A →i xtk(ϖ y w xi = + - ∀ ∈→tk k tk ktk∈A() () ()i µ µi ix→M( ) ( ) exp ( ),x = ∝ -Δ ∀ ∈→xx xtk f x tk f x tk tk ( ) A →tk tk tk tk tk tk ∑() ( 1)i i() ( 1)→x→M tk x tkx(c cλtk qtk tk tk tki q i q λ) = -ln e ∑∈ A() ( 1)tk tkµ µµ µ- -) )Mi a-( )x( ) ( )( (M→Mtk x tk x x x xi→∈x A1 0tk tk tk tktk q()i q Decode and generate LLRs {λa (c qtk),;∀}Q µM ()itk tk→x tk tkq i q ∏q=1( ) ;(c c=xexp 1 exp+()tk tk ⋅λλ a(a (( cti q()k)))),x∀ ∈A() ()i µ µix f tk x tk tk →( ) ( ),;x=M→tk tk tk tk x x∀ ∈A() () 2 ()f w tk f w tki ν σ→(ϖ y w x 2)x∑ϑf tk = + - ∀ ∈tk ( )x 2ˆ2,A →ii xtktk k tk ktk∈Ai x xµ()µ→tk x f tk(( )tk tk i)xˆx f→ =x∑tktk tk∈A A x∑t()i ;x f tnk →tk tk ( )xk ∈2i ( )()x xµtk x f tk →tk tk (i )νx f x f→=x∑t k∈ x A∑t k∈Ai()µi ( )x-xˆ() 2→tk tk tk tkx f tk →tk tk End for Output:∀ ∈(tk x ν w ν(i),() () ()i i i ) D ˆ ˆ,:,,.x f x f f w f w→→→→tk tk tk tk tk k tk k

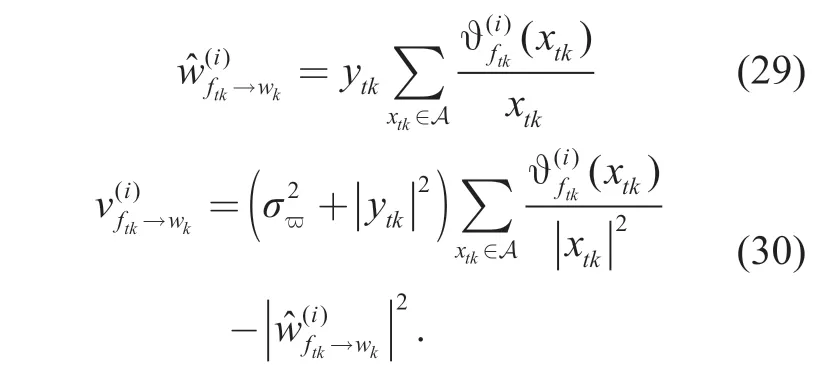
At theith turbo iteration of the BP-GA for symbol detection,we formulate the message passing from the symbol detection part to the channel estimation part.As presented in Table I,in lines 3-6,the distribution of the message passing fromxtkto Mtkis intricate as it is a mixture of Gaussian functions,which leads to a high complexity to calculate.Our method is to project the intractable distribution into a Gaussian distribution,which is expressed only by its mean and covariance.In lines 7-8,the apriorilog-likelihood ratio and the extrinsic log-likelihood ratio is obtained through the decoder.Next in lines 9-12,the message passing from the variable nodextkto the function nodeftkis derived based on the framework of belief propagation algorithm.

4.3 Low-complexity implementation

Observing the expression ofandobtained by the channel estimation,the main computational burden comes from matrix inversions,which results in a computational complexity of O(Kn3).To reduce the complexity,we expand the formula through the Woodbury matrix identity at first

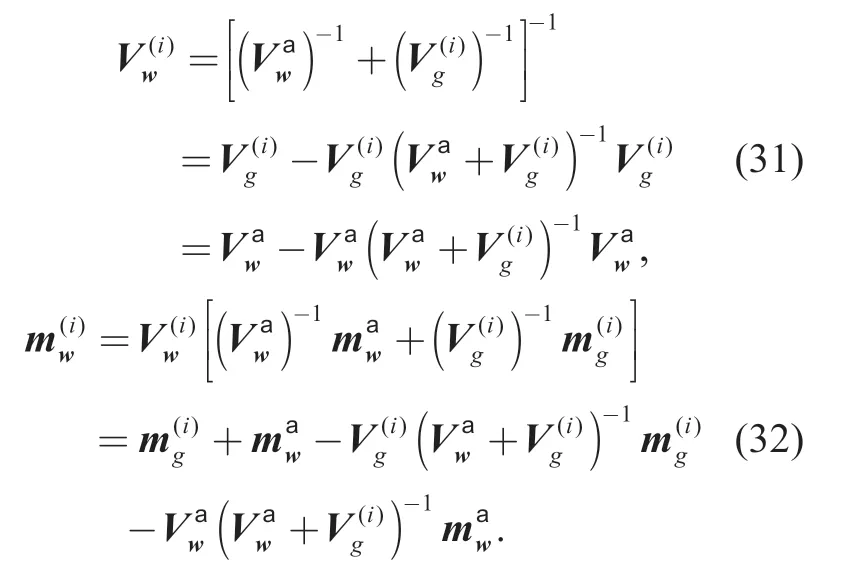
We can express the matrix inversion as

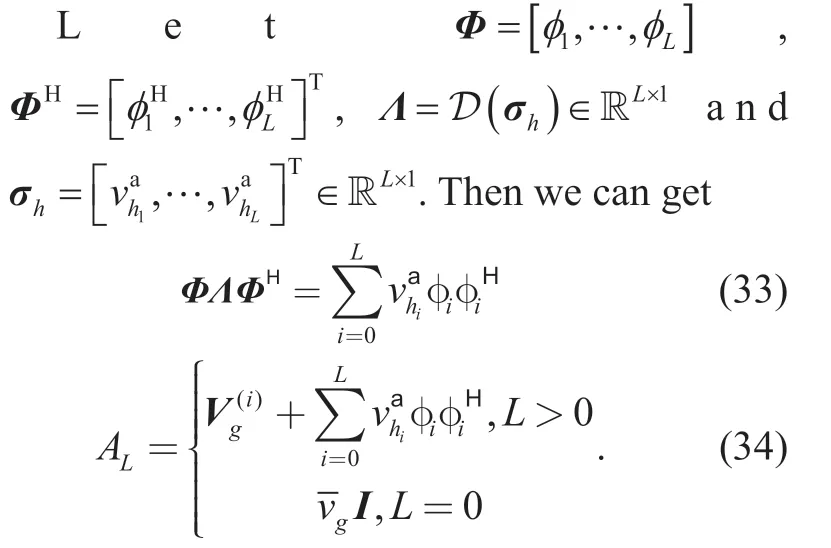
With Sherman-Morrison formula [28],we could get the iterative formula as follows

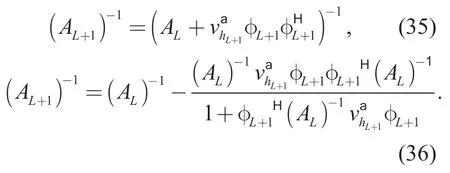
From (34),we can implement matrix inversion by means of recursion.AL+1-1will be calculated when we getAL-1.Through recursion,we find that we only need the inversion ofA0=whereA0is a diagonal matrix reducing the complexity of the algorithm from O(Kn3) to O(Kn2L).The number ofLsis much smaller thanKn.At this point,the channel estimation complexity isfar below

As presented in Table II,in lines 5-7,we put forward a recursion method instead of matrix inversion to reduce the complexity of the algorithm.The mean and covariance of the distribution ofwkis derived in lines 8-12.After that,we get the message passing fromwktoftkwith its mean and covariance based on the framework of expectation propagation algorithm in lines 13-16.

V.EXPERIMENTAL RESULTS

Let us consider an OFDMA system work at the central frequencyfc=2 GHz in a bandwidthB=10 MHz.The OFDMA system comprisesK=2048 subcarriers,which are shared byN=8 users with single antenna.Reserving used as guard subcarriers,each user is assignedKn=216 subcarriers.The channel power-delay profiles (PDP) of each user is generated according to the long-duration vehicle B in ITU-R channel model [35] with six pathsLS=6; It is assumed the channel is static in one OFDM symbol but variant in one frameT=25 and the CP lengthLCP=200 is longer than the maximum multipath delayL=193.For all results,we used irregular LDPC codes with code-word length 810 and rate of 1/2,interleaved by a S-random inter-leaver withS=32.4QAM modulation with Gray-mapping is used targeting on a spectral efficiency of 1 bit per subcarrier.We compare the proposed JCESD algorithm with LMMSE and LS channel estimation algorithm in terms of the normalized mean square error (NMSE).The NMSE is defined as

Table II.Low-Complexity channel estimation part at the ith turbo iteration.Input:∀ ∈(tk w ν,:,,) D ˆ() ()i if w f w→a a.→ ,V mtk k tk k h h(■ ■■■-1= …DAi Initialization:(m ΦmV Φ 0) =1/ ,,1/ ,ν() ()f w f wi→t1 1ν→tK K n n T)a a a Hw ,h w =ΦΛ.For {i L= -0:1s } do -1 H A v A+1)- -1= -( ) (1+φ 1(A A )φφ a Hi+1 i1 i1(i h i + +-1i i ()-1A v a i+1φ i1+ +i h i) 1 End for(V V a+ =w g()i)-1 (A)-1;L() () ()i ■i ˆ ˆ,,;T i mg f w f w= …■w wt1 1→ →■tK K ■() () ()i Vg f w f w=D(■ ■i ,,;T)ν ν…i ■t 1 1→ →tK K ■( g)-1 ;m m V V V m() ()i a a a a i V V VV V Vw = - +w w w w( a )-1 ;For (tk,)∈D do ν ν() () () () ()i i i i iw = - +g g g g w() () ()i (v )- -1■i 1= -( ) -1;iw f w f w→→■k tk k tk k ■■() ()i i () ()i i =ν ■ ■■ ■wˆw f w f ˆm ww f wk tk k→→k tk k tk ■-→ ;■() ()i i vw f w■k ν→tk k ■End for Output:∀ ∈(tk w ν() ()i i ) D ˆw f w f ,:,.→→k tk k tk

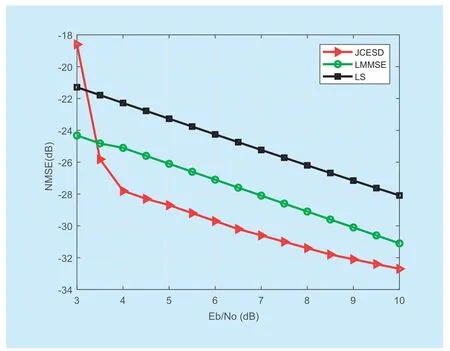
Fig.2.NMSE versus Eb / N0,4QAM,K p= 2.

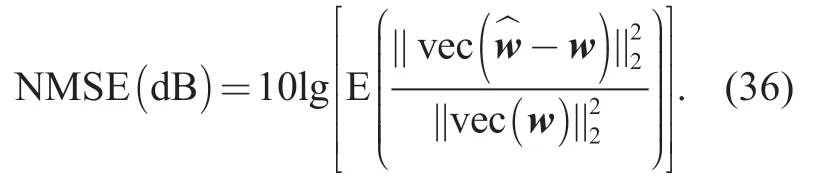
wheredenotes the output of channel estimator.

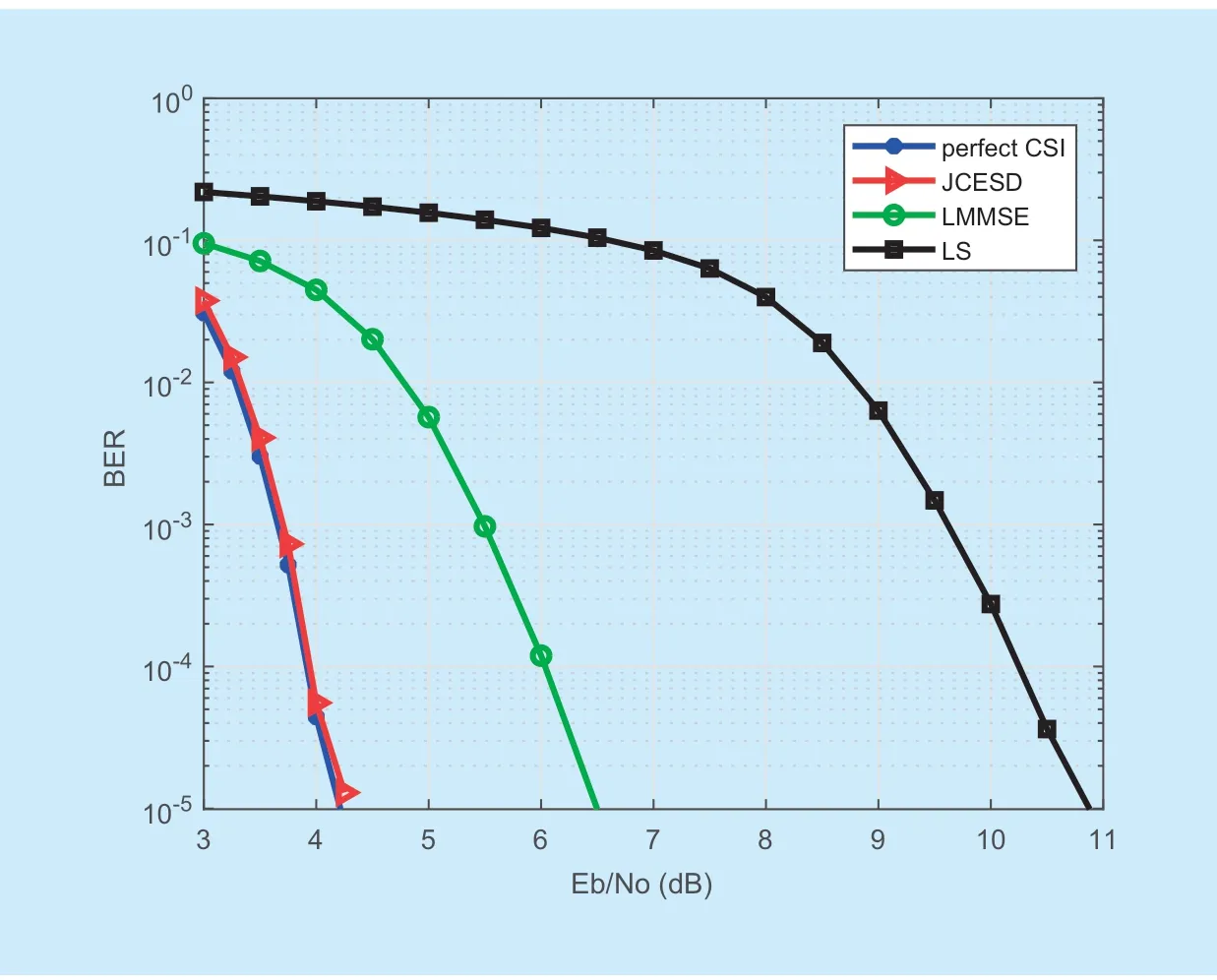
Fig.3.BER versus Eb / N0,4QAM,K p= 2.

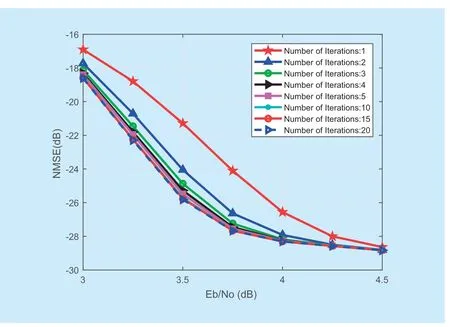
Fig.4.NMSE versus Eb / N0with JECSD,4QAM,Kp=2.

Figure 2 presents the NMSE performance of frequency-domain channel estimates versusEb/N0in the OFDMA system.Pilot intervalKp=2,and the maximum of 20 iterations are used in JCESD algorithm.We can conclude that the channel estimation performance in the JCESD algorithm is much better than the LS estimator and is superior to the LMMSE estimator by about 3 dB when the target of NMSE is -30 dB.At the initial channel estimation,the estimator performance in the JCESD algorithm is equivalent to the LMMSE estimator since only pilots contribute to channel estimation.We can obtain more accurate data through the decoder and it becomes a data-aided LMMSE estimator for the following turbo iterations.As the decoder outputs more accurate bit estimate,the channel estimation becomes more accurate as well.By contrast,when there are many errors in decoding,incorrect data can lead to the performance degradation of channel estimation,which is the reason for that JCESD algorithm turns less useful whenEb/N0＜ 3.5 dB.However,in order to ensure the quality of communication,most of the receivers work at BER = 10-5.In this case,the performance of the JCESD algorithm is significantly better than other algorithms.

Figure 3 shows the BER performance versusEb/N0in the OFDMA system.It can be observed that the BER curve of the JCESD algorithm is waterfall-type and close to the performance bound of perfectly known channel state information.Compared with the traditional MMSE equalizers using LMMSE channel estimation,the proposed JCESD algorithm can improve the BER performance by 2-2.5 dB when the target of BER is 10-5.In addition,the BER performance of JCESD algorithm outperforms the scheme using LS and MMSE equalizers about 6.5 dB.From figure 2 and figure 3,we can conclude that the BER performance can reach 10-5when the performance of channel estimation MMSE reaches about -28 dB in this system.

Figure 4 and figure 5 show the NMSE performance of channel estimation and BER performance versusEb/N0for different number of turbo iterations,respectively.According to the channel power-delay profiles of the ITU-R channel,we can calculate to get the optimal pilot intervalKp=2 [36].It can be observed from figure 4 and figure 5 that the proposed algorithm can converge.When the number of iterations is up to 5 times,the performance of NMSE and BER gets close to the best performance of the JCESD algorithm itself.

Figure 6 shows the NMSE performance of frequency-domain channel estimates versus number of iterations.The output of the decoder provides more accurate symbol estimation and it helps a lot to reduce the pilot number.The proposed JCESD algorithm do not need to follow the pilot interval calculated according to the correlation time [36],and the number of pilots used can be reduced.It can be seen from figure 6 that when the pilot intervalKp=4,the JCESD channel estimation performance outperform that of the LMMSE algorithm withKp=2 after three or more iterations.When the pilot interval isKp=4,the JCESD channel estimation performance is better than the LMMSE algorithm pilot intervalKp=2 by three or more iterations.When the pilot interval isKp=8,after three or more iterations,the JCESD channel estimation performance can approach to the LMMSE algorithm even with pilot interval isKp=4.It can be obtained that the proposed algorithm can reduce the pilot overhead by about 50% compared to the LMMSE algorithm.

VI.CONCLUSION

This paper presents a joint iterative channel estimation and symbol detection (JCESD) algorithm by using message passing algorithm.Expectation propagation (EP) and belief propagation (BP) with the aid of Gaussian approximation were applied for the channel estimation and symbol detection,respectively.The implementation complexity of our JCESD algorithm drops fromper iteration with the aid of Sherman-Morrison formula.Experimental simulations showed our proposed algorithm can approach to the bound of known channel state information within 0.1 dB,and the performance is 2-3 dB better than LMMSE and MMSE equalizers.In addition,the JCESD algorithm is capable of decreasing about 50% pilot overhead compared to the traditional LMMSE algorithm.

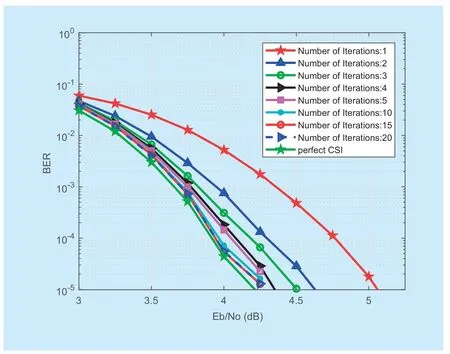
Fig.5.BER versus Eb / N0with JECSD,4QAM,Kp=2.

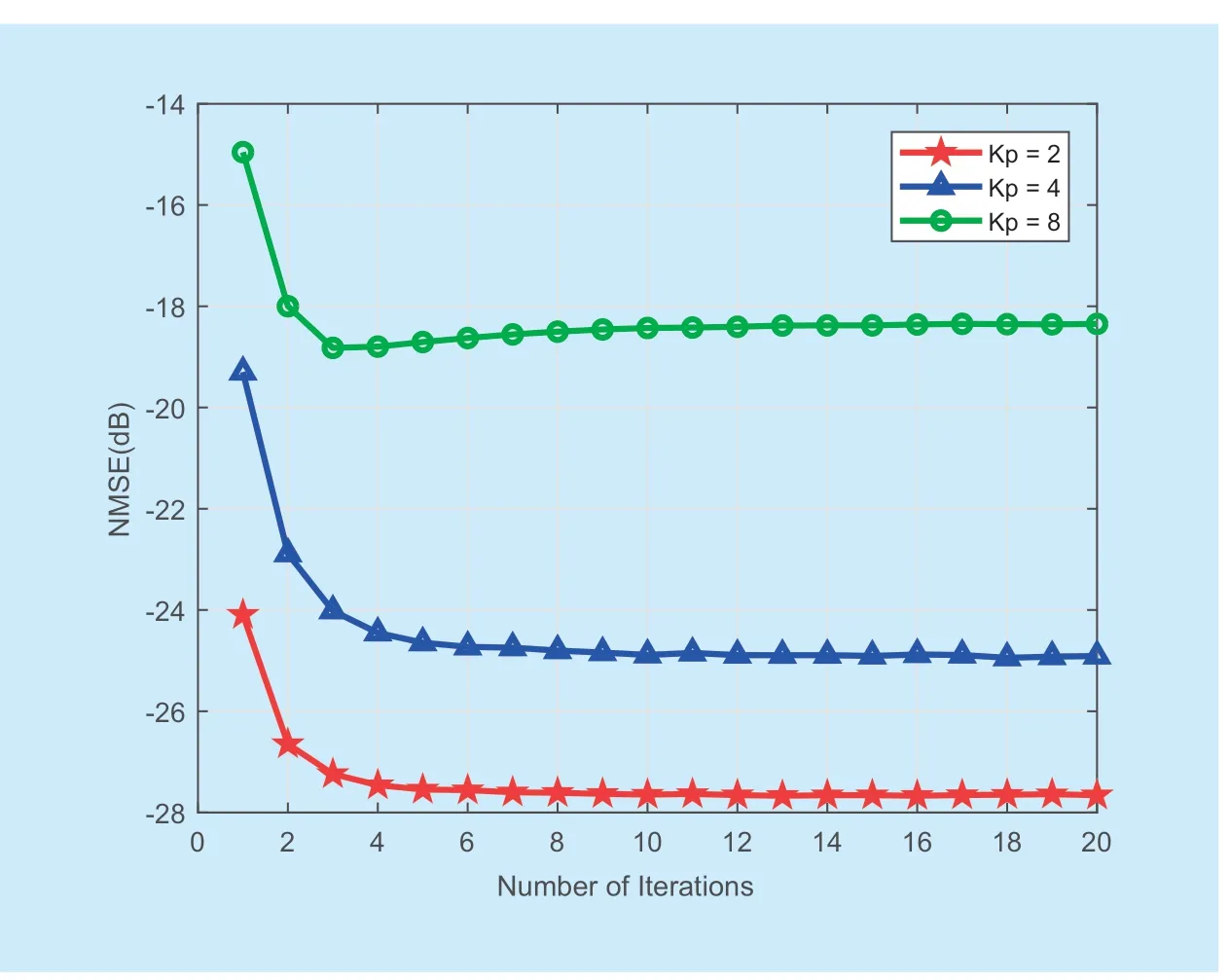
Fig.6.BER versus the number of iteration with JECSD,4QAM,Kp=2.