A Game Theoretic Approach for Hierarchical Caching Resource Sharing in 5G Networks with Virtualization

Renchao Xie＊,Jun Wu,Rui Wang,Tao Huang

1 State Key Laboratory of Network and Switching Technology,Beijing University of Posts and Telecommunications,Beijing 100876,China

2 Purple Mountain Laboratories,Nanjing 211111,China

3 Dhurakij Pundit University,110/1-4 Prachachuen Rd.,Laksi,Bangkok 10210,Thailand

4 Institute of Sensing Technology and Business,BUPT,214315,China

Abstract: Caching and virtualization have been considered as the promising techniques in 5G Networks.In 5G networks with virtualization,the caching resources deployed by infrastructure providers (InPs) can be abstracted into isolated slices and transparently shared by mobile virtual network operators (MVNOs).In this case,one of the most important issues is how the MVNOs to share the caching resource.To solve this issue,different from previous works,a hierarchical caching architecture that core network and radio access network (RAN) have the caching capability in 5G networks with virtualization is first considered in this paper.Then,we study the problem of hierarchical caching resource sharing for MVNOs,and a competitive game to maximize their expectation revenue based on the oligopoly market model is formulated.As it is a hard problem to find the optimal solution in the hierarchical caching resource sharing problem,we decompose the optimization problem into two independent caching resource sharing problems in RAN and core network,respectively.Then the local optimal solutions are solved and the global Nash equilibrium solution is achieved.Finally,simulation results are illustrated to demonstrate the performance of the proposed scheme.

Keywords: hierarchical caching; resource sharing; game theory; oligopoly market model; 5G networks

I.INTRODUCTION

The mobile Internet and Internet of Things (IoT) have been considered as the most important service application in the future mobile networks,which make the mobile data traffic grow dramatically.According to a recent report from Cisco [1],mobile data traffic will increase 7-fold between 2017 and 2022.The explosive growth of mobile data traffic brings huge challenges for the mobile network.In order to cope with these challenges,a promising solution is to deploy caching in the future 5G networks [2]-[5].By caching popular contents in mobile network,most requests can be served in the nearby side to users,therefore the load of original servers,load of links and average delay can be decreased significantly [6].

Since caching technique has been proposed,the problem of the cache deployment and allocation problem at the radio access network (RAN) have been done by many researchers [7]-[14].The authors in [7] study the problem of context-aware proactive caching by considering the content caching in small base stations (SBSs) with storage limitations,then a novel algorithm to maximize the number of cache hits is proposed.In [8],the problem of optimal cooperative content caching and delivery policy in heterogeneous cellular network (HetNet) is studied,then the authors formulate a cooperative content caching problem as an integer-linear programming problem,and propose a hierarchical primal-dual decomposition method to solve the optimization problem.The authors in [9] study the problem of energy efficiency of downlink networks with caching at base stations,then the closed-form expression of the approximated energy efficiency is derived.As vehicular content demand brings significant challenges for 5G network,the authors in [10] proposed a novel theoretical framework to characterize the tradeoff among computing,cache,and communication resources required by the mobile edge network to fulfill the task of content delivery.The caching policies for layered video content delivery is studied by authors in [11].In [12],two scenarios are considered where caching is performed either at a small base station,or directly at the user terminals,then the joint design of the transmission and caching policy is proposed by authors.In [13],the authors study the problem of optimal proactive caching in mobile network,then the fundamental bounds on the minimum possible cost achievable has been established as a function of the prediction uncertainties.And in [14],the problem of proactive caching in large-scale 5G mobile edge networks is studied,then a Stackelberg game-based alternating direction method of multipliers for edge caching is proposed.

Although the caching problem in mobile networks have been done in many works,most of them focus on the problem of caching performance optimization,such as proactive caching strategy,energy efficiency content placement and delivery and so on.However,with the development of software defined networking (SDN) and network function virtualization (NFV) technologies,virtualization has been proposed as a key technique in future 5G network.In this case,the caching resource deployed by the infrastructure providers (InPs) can be abstracted into isolated slices and transparently shared by mobile virtual network operators (MVNOs),which have also attracted the researchers’ attention.The authors in [15] consider in-network caching combining with network slicing,and propose an efficient caching resource allocation scheme for network slicing in 5G core network.In [16],the authors investigate and discuss the state of the art and challenges for network sharing and slicing,while introduce a novel end-to-end network sharing architecture for dynamic spectrum management through multi-tenant slicing.The authors of [17] design the network management architectures enabled by SDN/NFV and study the problem of network service chaining (NSC) for the over-the-top (OTT) services.Then a distributed prioritization NSC management scheme for OTT application flows based on matching theory is proposed.Although some works have been exploited the benefits of NFV and network slicing,how to share the caching resource of 5G cellular networks with virtualization is still largely ignored,especially for the hierarchical caching architecture.Therefore,to fill this gap,based on our previous work [18],we further investigate the hierarchical caching architecture in 5G networks with virtualization in this paper,then we study the problem of hierarchical caching resource sharing problem among MVNOs,and a more detail caching sharing strategy is designed.The main contributions of this paper can be summarized as follows.

·As the core network and RAN can deploy caching respectively to improve the network performance as analyzed in [19],therefore we first consider the hierarchical caching architecture in 5G networks with virtualization.That is we consider a hierarchical caching architecture that core network and RAN have the caching capability,then caching resource deployed by the infrastructure providers (InPs) can be abstracted into isolated slices and transparently shared by MVNOs.

·Under this framework,one of the most important issue is how to share the hierarchical caching resource for MVNOs.In order to solve this issue,we formulate the problem of hierarchical caching resource sharing for MVNOs as a competitive game to maximize their expectation revenues based on the oligopoly market model.

·And due to finding the optimal solution in the hierarchical caching resource sharing problem brings huge computation complexity,therefore we decompose the optimization problem into two independent caching resource sharing problems in RAN and core network,respectively.Then the RAN caching resource sharing problem is modeled as a dynamic non-cooperative Cournot game,and local optimal solution is proposed by using an iterative algorithm based on the Newton-Raphson method.And to solve the caching sharing in core networks,we propose a request probability sorting algorithm in order to sort all the requests not served by base stations (BSs) in RAN.The probabilities of all requests arriving at the core network are sorted as a sequence in descending order through the algorithm and the local optimal caching resource at core network is obtained by using this sequence.Finally,based on the local optimal solutions at RAN and core network,the global Nash equilibrium solution is achieved.

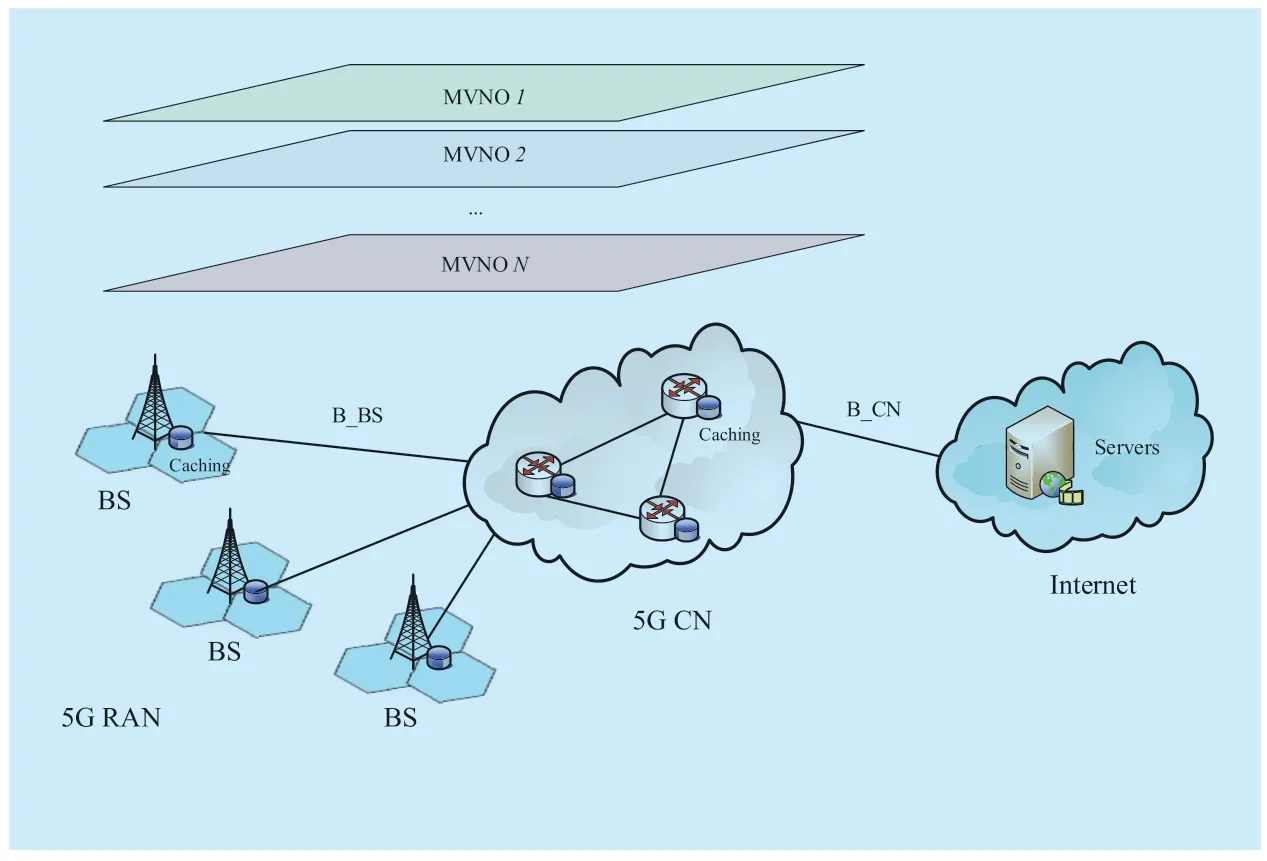
Fig.1.Hierarchical caching architecture in 5G Networks with virtualization.

Finally numerical simulation results are illustrated to demonstrated the performance of the proposed hierarchical caching resource sharing scheme.

The rest of this paper is organized as follows.In Section II,we first describe the system model,and then the hierarchical caching resource sharing problem in 5G networks with virtualization is formulated.The dynamic non-cooperative Cournot game model of the RAN caching resource sharing problem with its local optimal solution,the model of the CN caching resource sharing problem with its local optimal solution and the algorithm for the global equilibrium solution are presented respectively in Section III.In Section IV,the simulation results are discussed.Finally,we conclude the study in Section V.

II.SYSTEM DESCRIPTION

In this section,the hierarchical caching architecture for 5G networks with virtualization is first presented in Subsection II-A.Then the hierarchical caching resource sharing problem to maximize revenues of MVNOs is formulated as a game theoretical problem in Subsection II-B.

2.1 System model

We consider a 5G cellular network system owned by infrastructure provider (InP) consisting of a core network (CN) and radio access network (RAN) as shown in figure 1.For ease of illustration,we regard all the routers in CN as a CN node in the latter of our paper.We assume that there are totalMBSs in the radio access network with the corresponding set R= …{1,2,,M},and all the BSs and the CN node are cache-enabled so that a hierarchical caching system is consisted to provide the cooperative cache capability with virtualization.And each MVNO can allocate the caching resources within the slice to its subscribed users.Here,we assume that there are totalNMVNOs with the corresponding set N= …{1,2,3,,N} in the system to share the caching resource.

Under this framework,as all the physical infrastructures of the 5G network system are owned by InP and there exist mutual competitions among MVNOs during sharing the caching resource,therefore one of the most important critical issue is how to design an efficient caching resource sharing mechanism for MVNOs,so that the expectation revenue of the InP and MVNOs can be maximized.To solve this problem,a game theoretic approach using the oligopoly market model is studied in this paper.We assume InP as a monopolist which would offer a selling price to sell its cache resources relying on the demand of the MVNO.And as the players,the MVNOs will mutually compete caching resources based on the selling price to maximize their revenues.Here,the revenue of MVNOs is defined as the total cost they can save.

The detailed optimization problem is modelled in the next subsection.

2.2 Problem formulation

Based on the assumption of Subsection II-A,if we assume that the demand of caching resource for thenthMVNO at the BSs and CN node isqn= {qn,1,qn,2,… ,qn,M,qn,CN},where the firstMelements denote the demand of caching resource at BS nodes,and the last element denotes the demand of caching resource at the CN node.As the monopolist in this oligopoly market model,the InP offers the monopoly caching price corresponding to the caching resource demand of all MVNOs.To simplify the analysis of our problem,we assume InP charges all MVNOs with the same price for RAN caching,however,the price of CN caching is different to the price of RAN caching.Letb1=(QBS) andb2=(QCN) be the monopoly caching price determined by InP at RAN and CN node corresponding to the cache demand of MVNOs,whereQCN={q1,CN,q2,CN,q3,CN,… ,qN,CN} are the sets of strategies of total amount of caching resource demands for all MVNOs at RAN and the CN node,respectively.Inspired by [20],we can give the price functions of caching resource as follows.

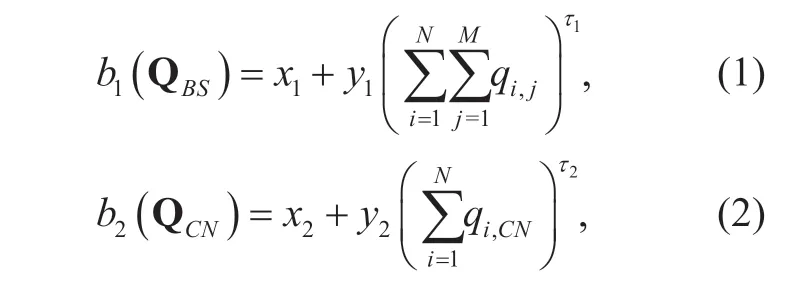
wherex1,x2,y1andy2are non-negative constants.We assumeτ1≥1 andτ2≥1 to make the price functions as convex functions.

Given the price of caching resource,each MVNO expects to optimize its revenue.Here,we present the revenue of each MVNO in the form of cost saving [6][21].We assume that the number of content requests belonging to MVNOnn,∈N arriving at the BSmm,∈R denote asrnm,,and the mean size (Mb) of all the contents of MVNOnisSn[21]-[23],the costs for RAN backhaul resources and CN link resource of transmitting per unit Mb data are denoted asBBSandBCN,respectively.In this case,if the system architecture is without deploying the cache,all the requests beget the cost of transmitting through the entire path from the user’s device,through the packet data network gateway (PGW),then to the source content provider [23].Therefore,the total cost for MVNOnn,∈N can be expressed as follows.

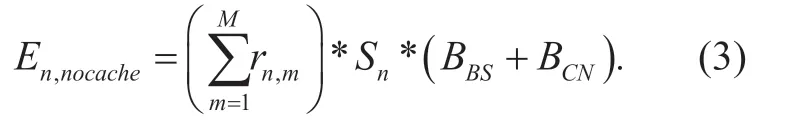
Now when the network deploys the caching,the MVNOs can cache them contents in the BSs or CN node,the request can be served in the BSs or CN node directly without redirecting to the source server.For this reason,similar to [23],the total cost of MVNOnn,∈N can be expressed as

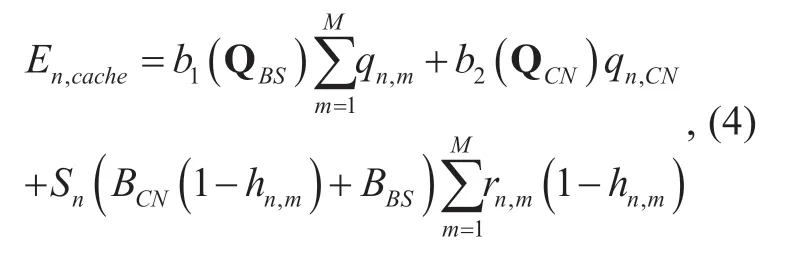
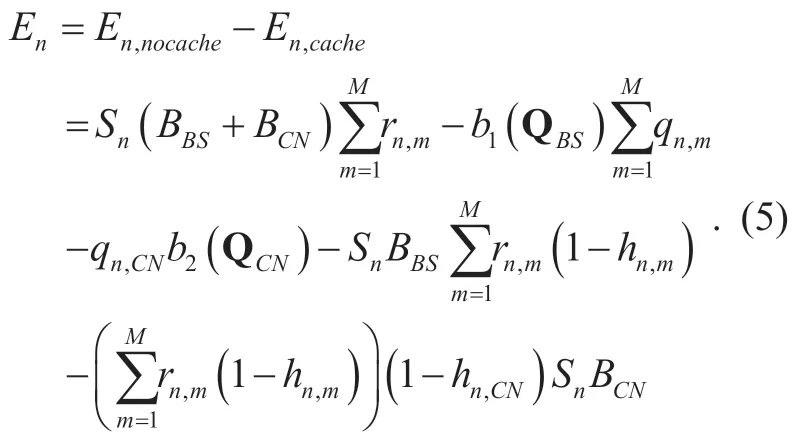
Based on (5),when the price of caching is offered by the InP,all the MVNOs are expected to compete certain caching resources at the BSs and the CN node to maximize the cost saving.And when the determined content caching strategy is used by the MVNO,the request hit ratio ofhnm,andhnCN,can be obtained,then the demand of caching resource at the BSs and CN node for the MVNOs can be solved.

III.THE SOLUTION OF CACHING RESOURCE SHARING PROBLEMS

In this section,we solve the hierarchical caching sharing problem as modeled in Subsection II-B.By observing equation (5),due to the hierarchical property,we know that the optimal caching resource demands at BS and CN nodes are largely relying on the request hit ratio ofhnm,andhnCN,,which are affected by each other.Furthermore,usually it is hard to get closed expressions of the request hit ratio ofhnm,andhnCN,,which is usually related to the caching strategy.In this case,to find the joint optimal solution is a hard problem.Therefore,in order to make the hierarchical caching resource sharing problem tractable,we first decompose the optimization problem into two subproblems in Subsection III-A,that is we study the RAN caching resource sharing problem and the CN caching resource sharing problem separately.Then some assumptions for the request hit ratio ofhnm,andhnCN,are given.Then in Subsection III-B,the RAN caching resource sharing problem is modeled as a dynamic non-cooperative Cournot game [21],and then we use a Newton-Raphson method based iterative algorithm to obtain the local optimal solution of the Cournot game.In Subsection III-C,we study the caching resource sharing problem at the CN node among MVNOs.Then the local optimal solution of the CN caching resource sharing problem and the global equilibrium solution of the virtualized hierarchical caching resource sharing problem are given.

3.1 The decomposition of caching resource sharing problem

Due to the request hits ratio ofhnm,andhnCN,are affected by each other,the problem in (5) is hard to solve.Therefore,we first decompose the optimization problem into two subproblems:RAN caching resource sharing problem and the CN caching resource sharing problem separately.

We first let total amount of the requests of MVNOnarriving at the CN node be

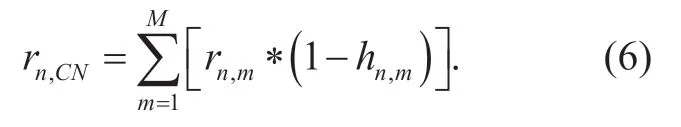
Then the optimization problem (5) for cost saving for the MVNOnn,∈N can be decomposed into two subproblems as follows.

SubProb.1:

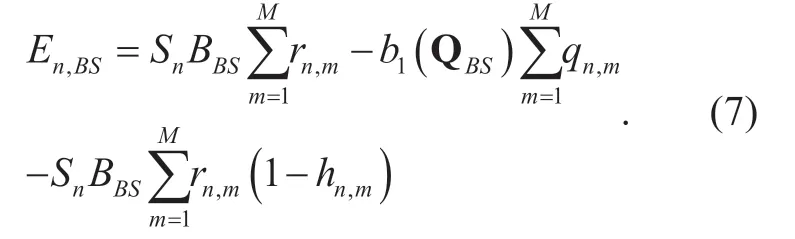
SubProb.2:

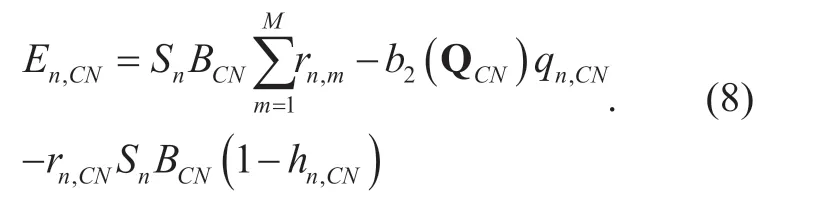
Then,in order to get the expressions of the request hit ratios,we first make some assumptions for the request hit ratioshnm,andhnCN,.As proposed in [24][25],we suppose that the hit rate of each content follows a Zipf-like distribution,which is commonly used in the study of content popularity in communication networks.We assume that for each MVNOnn,∈N,the total number of contents it owns isF.According to the Zipf-like distribution,the probability of requesting a content at rankkout ofFavailable contents can be expressed as

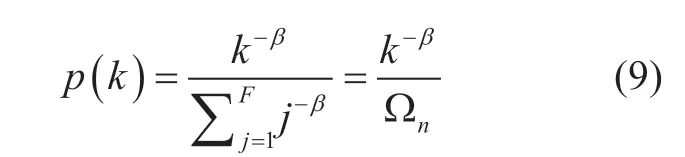
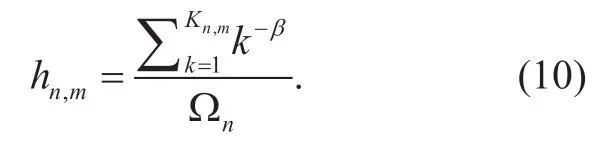
Inspired by [24],we can approximately obtain

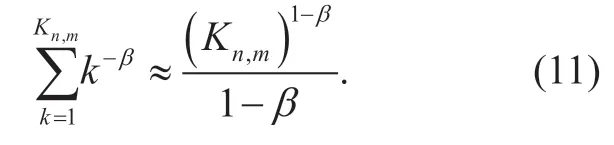
Consequently,for Zipf-like distributions,the cumulative requested probability of the topKnm,popular contents can be presented as

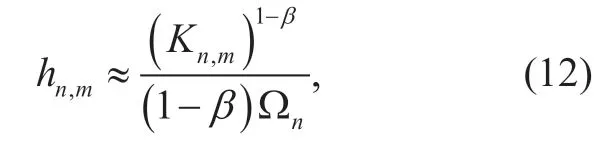
whereKn,m=qn,m/Sn.

Then,due to the hierarchical caching property,it is noted that the request hit ratio for MVNOnin the CN node,i.e.,hnCN,,cannot be expressed Zipf-like distributions.This is because some requests have been served by cached contents at BS nodes.Besides,as the requests arriving at the CN node are the sum of all requests not served by BS caching,the requests arriving at CN node don’t follow Zipf-like distribution.Therefore,hnCN,can be computed when all the RAN caches are already allocated.In Subsection III-B,we first consider the caching resource sharing problem in RAN.

3.2 The solution of ran caching resource sharing

Based on the decomposition of the optimization problem and the assumption of caching hit ratios in Subsection III-A,and since the revenues of each MVNO are mutually independent,the revenue of MVNOnat BS m can be expressed asEnmBS,,as follows.

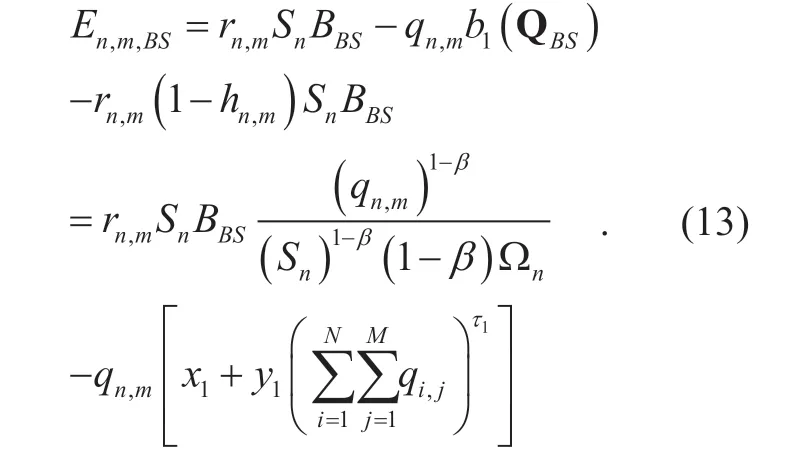
Obviously,the objective of the Cournot game in (13) is to maximize the revenue of each MVNO.As the revenue of MVNOnatMBS nodes are mutually independent,the local optimal solution of the Cournot game is equivalent to the maximum value ofEnmBS,,.As a result,we first prove thatEnmBS,,exists a unique maximum value,then propose an iterative algorithm based on Newton-Raphson method to obtain the local optimal solution of the Cournot game.

Theorem 1:EnmBS,,is a strictly concave function in the interval ofqnm,＞0,and there exists a unique maximum value

Proof:We can obtain the first derivative ofEnmBS,,presented as follows.

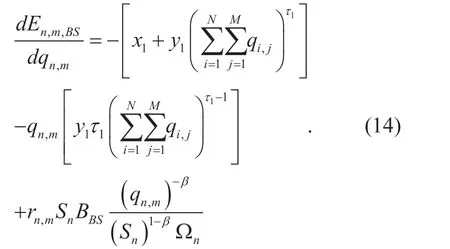
Similarly,the second derivative ofEnmBS,,is presented as follows.

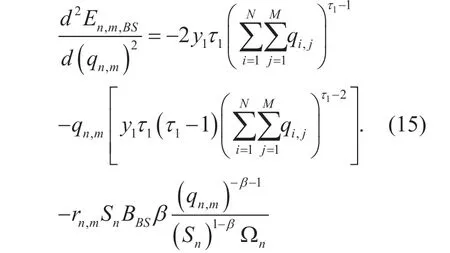
In equation (15),τ1is defined asτ1≥1,βis defined as 0 ＜β＜ 1,andrn,m,Sn,BBS,Ωnare positive constants.Thus,inequations presented as follows must be simultaneously established.

Algorithm 1.Iterative algorithm optimal solution of the RAN cachi based on Newton-Raphson method for the local ng resource sharing problem.begin 1.Initialization:given the initial caching resource demands at BS nodes:■0q q 0 1,1 1,M ■ QiniBS=■■⋮ ⋱ ⋮■■0… …■,(20)■q q 0N,1 ,NM ■■ and the control accuracy ε＞0.2.for each n∈N 3.for each m∈R 4.k←0 5.while ■ ■■ ■■ ■■ ■dE dq≥ε do q q nmBS,,nm,k k k,,+1= -nm nm■ ■■ ■■ ■■ ■dE dq nmBS,,nm,k ■ ■■ ■■ ■2 (.(21)dE dqnmBS ,,■ ■nm ,)2k 6.k k← +1 7.end while 8.Output the approximate optimal caching space demand q qbest knm nm ,,= .9.end for 10.end for 11.Output the local optimal solution:best best ■q q 1,1 1,M ■ QbestBS=■■⋮ ⋱ ⋮■■… …■.(22)best best ■q qN,1 ,NM ■■12.end

Therefore,we can obtain

is always established in the interval ofqnm,＞0.And that is to say,EnmBS,,is a strictly concavefunction in the interval ofqnm,＞0.Furthermore,we can know that the first derivative is monotonically decreasing in the interval ofqnm,＞0.Besides,as inequations

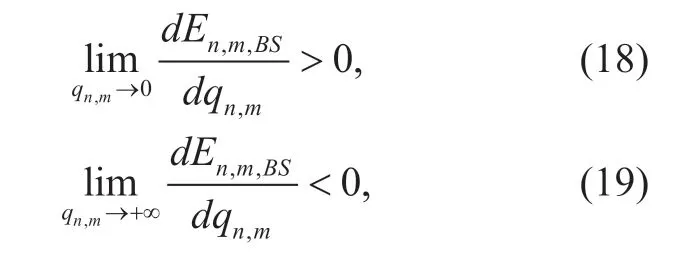
are simultaneously established,we can obtain thatEnmBS,,is firstly monotonically increasing,then monotonically decreasing in the interval ofqnm,＞0.Therefore,EnmBS,,exists a unique maximum value,and Theorem 1 is proved.

Based on Theorem 1,we can obtain the local optimal solution of the RAN caching resource sharing problem by using an iterative algorithm based on Newton--Raphson method [26].The proposed algorithm is given in Algorithm 1.

In a practical caching resource competing scenario,only the price information from InP can be observed by MVNOs.Because all the MVNOs are rational in maximizing their revenues,they can use the marginal profit function to adjust their caching resource demands.is defined as the caching resource demand of MVNOnat BSmin iterationi,andis defined similarly.Therefore,the relationship of caching resource demands in current iteration and the next iteration is given as follows [20]:

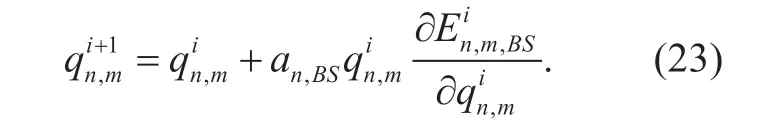
whereanBS,denotes the learning rate of MVNOnin the RAN caching resource sharing problem,and the expression ofis given in equation (14).With a proper value ofan,BS,the caching resource demand will converge gradually and reach the Nash equilibrium.At the equilibrium point,we haveThe equation (23) is used for updating the caching resource demands at BS nodes in the algorithm for global equilibrium solution of the virtualized hierarchical caching resource sharing problem.

3.2 The solution of CN caching resource sharing

In this subsection,we study the caching resource sharing problem at the CN node for MVNOs in the case that caches in BS nodes are already allocated.As the request hit ratio at CN nodehnCN,cannot be expressed by the Zipf-like distribution,we propose a request probability sorting algorithm to obtain the expression ofhnCN,.Then according to the nature ofEnCN,,i.e.,the revenue of MVONnat CN node,a discrete maximum value look up algorithm to obtain the local optimal solution is presented.Finally,an iteration algorithm to obtain the global equilibrium solution of the hierarchical caching resource sharing problem in 5G networks with virtualization is given at last.

The architecture of the CN caching resource sharing problem can be modeled with one CN node with certain amount of caches and a link connecting to the Internet.Requests arriving at the CN node are the requests not served in the corresponded BS nodes.All the MVNOs compete for the caching resource at the CN node to cache contents for the reason of saving link costs.Similar to the RAN caching resource sharing problem,the cost saving for MVNOncan be rewrite as

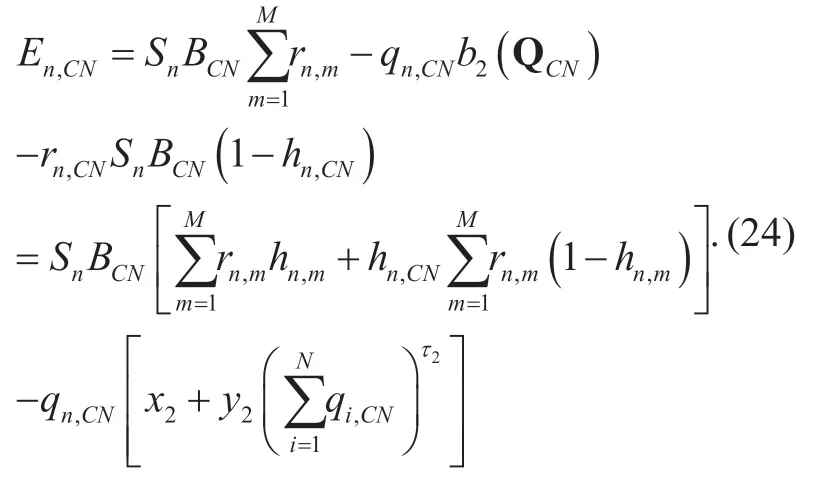
All expressions of the notations in equation (24) are given except the explicit expression ofhnCN,.As aforementioned,for MVNOnat BSm,since the requests belonging to the topKnm,popular contents are served directly in the BS cache,and the number of cached contents at different BS nodes are different,the expression ofhnCN,cannot be expressed by Zipf-like distributions.In order to obtain the expression ofhnCN,,a request probability sorting algorithm is proposed as follows in Algorithm 2.

With the expression ofhnCN,,we can further write the equation (24) as the following equation.

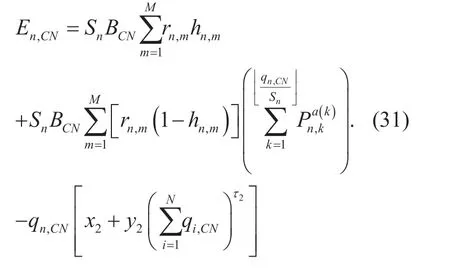
Algorithm 2.Request probability sorting algorithm for the expression of hnCN,.begin.1.Compute the number of cached contents in BS nodes:best Nnm,=qSnm ,n.(25)2.Sort the highest rank of contents arriving at the CN node from all the BS nodes{N N N 1,1,,1} in the ascending order given as:G G G G+ +… +n,1 ,2 ,nnM) ()… ()},(26) where gm() denotes the corresponding BS number of Gmg g gM(1 2n { 1 2:,,,Mgm()3.Compute the normalized requested probabilities of all the contents belonging to MVNO n from rank a G= 1g(1) to a N= ntotal:-β a()=Ω■ngaG,(≥),(27) where Pa r■nnCNr■■,■■gaG(∑≥)■■gaG(∑≥)rngaG,(≥) indicates the total amount of requests of the content at ranka.4.Sort Pa() in the descending order presenting as follows:P p p p) ()… ()} (28) where Y N= ntotal,and ay() denotes the rank of the content in Zipf-like distributions.5.As the amount of cache at CN node for MVNO n is qnCN,,the content number cached in the CN cache can be presented as:(1 2n n n nY { a a aY,1 ,2 ,:,,,,qnCN KnCN,=■ ■■ ■■ ■,.(29) Thus sum of the top KnCN, requested probabilities in Pn is the hit ratio ofMVNOn at the CN node,i.e.,the expression of hnCN, can be obtained as follows:Sn,qnCNS KnCN ,()■ ■■ ■■ h P P,= =■ ().(30)nCN nk nk ak ak,∑ ∑,k=1k=n 1 end

In (31),hnCN,is a step function shown.Therefore,in order to discuss the nature ofEnCN,,we separateEnCN,into two parts:

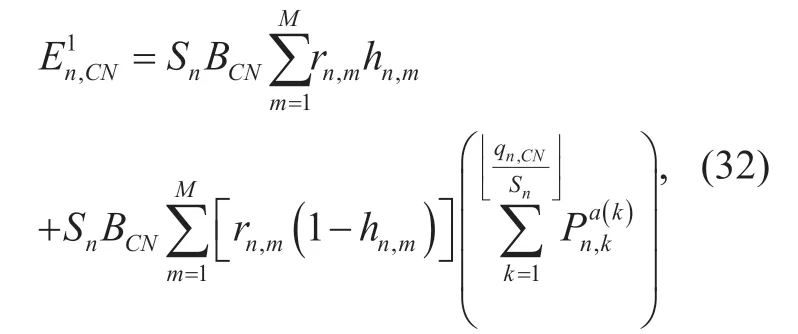
and

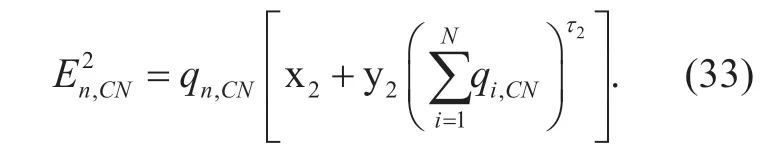
In,asrn,m,hn,mandBCNare constants,is a step function ofhn,CN.The value ofincreases whenqn,CN=jSn,wherej= 1,2,… ,and the growth value is given in (34).

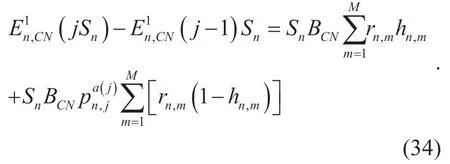
AsPnis a sequence in descending order and other notations are all constants,the increasing value ofdecreases whenjincreases tillThe value ofreachesto maximum whenin this case,value of the hit ratiohCNis 1.However,it is usually impossible under normal circumstances sinceis a considerable constant and the caching resource is limited at the CN node.

Obviously,is a monotonically increasing function.And we need the following theorem to obtain the maximum value of

Theorem 2:is a convex function in the interval ofqn,CN＞0.

Proof:The first derivative and the second derivative ofare given in equation (35) and (36) respectively as follows:

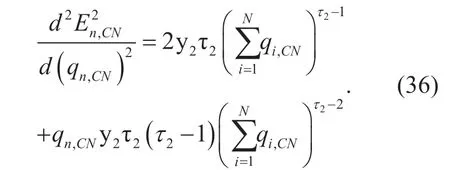
As all the notations in equation (36) are non-negative andτ2is subjected toτ2≥1,it is obvious thatis established whenqn,CN＞0.Thusis convex in the interval ofqn,CN＞0,and theorem 2 is proved.

Based on Theorem 2 and the nature ofProposition 1 is given as follows:

Proposition 1:There existKntotallocal maximums inEn,CN,and the local maximums appear whenqn,CN=jSn,wherej= 1,2,… ,

According to Theorem 2,we can know thatis monotonically non-decreasing whenqnCN,＞0.Therefore,based on Theorem 2,the nature ofand the nature ofTheorem 3is given as follows:

Theorem 3:All the local maximums ofEn,CNare non-positive and the sequence of local maximums is decreasing when the first local maximum(Sn) is non-positive.When the first local maximum is positive,the sequence of local maximums is firstly in increasing order and then in decreasing order ifestablishes.

Proof:We define the three following sequences:

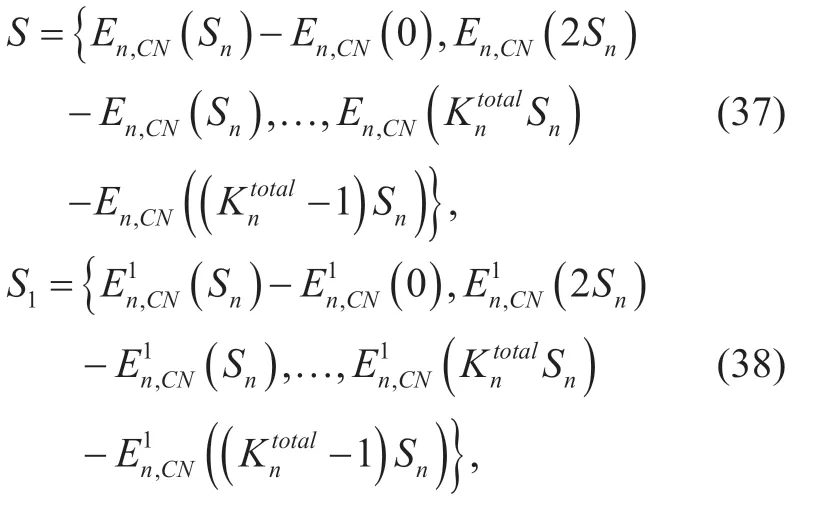
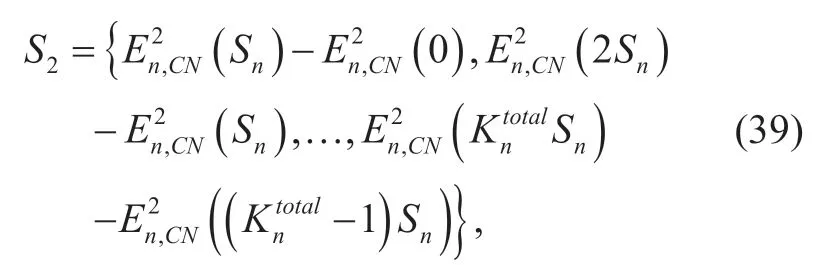
According to the equation (34),we know that the sequenceS1is in descending order,and all the elements are positive.Asis a convex function in the interval ofqnCN,＞0,which is proved in Theorem 2,we know that the sequenceS2is in non-decreasing order.Furthermore,it is obvious that

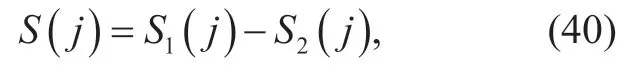
whereS(j),S1(j) andS2(j) are thejth element ofS,S1andS2respectively.As a result,the sequenceSis in descending order.As the sequenceSindicates the differences of adjacent maximums ofEn,CN,thus whenS1(1) -S2(1) ≤0,i.e.,the first local maximum ofEn,CNis non-positive,all the local maximums are non-positive and the sequence of local maximums is decreasing.WhenS1(1) -S2(1) ＞0,i.e.,the first local maximum ofEnCN,is positive,the sequence of local maximums is firstly in increasing order.Ifthe sequence of local maximums is firstly in increasing order,then in decreasing order,and ifthe sequence of local maximums is in non-decreasing order.Theorem 3 is proved.

It is noted that because of the individual rationality,when all the local maximums are non-positive,all the MVNOs will not buy any caching resource at CN node since caching contents will not earn any profit for MVNOs.Besides,the case that the sequence of local maximums is in non-decreasing order is usually impossible since the caching resource at CN node is always limited.

According to Theorem 3,when the sequence of local maximums is firstly in increasing order and then in decreasing order,we propose a discrete local maximum value look up algorithm to obtain the maximal profit for MVNOn.The algorithm is presented as follows:

Similar to the RAN caching resource sharing problem aforementioned,in the CN caching resource sharing problem,all the MVNOs can only adjust their caching resource demands at the CN node based on the pricing information from InP.Therefore,the relationship of caching resource demands in current iteration and the next iteration is given as follows:

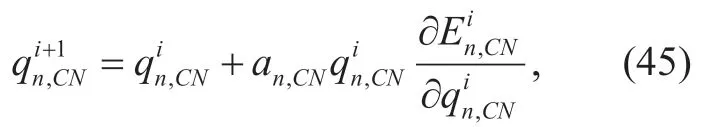
whereanCN,is the learning rate of MVNOnin the CN caching resource sharing problem.At the equilibrium point,we have

Therefore,with Algorithm 1,Algorithm 2 and Algorithm 3,the algorithm for global equilibrium solution of the hierarchical caching resource sharing problem in 5G networks with virtualization is given in Algorithm 4.

Algorithm 3.Discrete local maximum value look up algorithm for the maximal profit of MVNO n.begin 1.Initialization:given the expressions of hnm, based on equation (25),(12) and Algorithm 1,given the sequence Pn based on Algorithm 2 2.for each n∈N do 3.for i K=1:ntotal 4.Compute the local maximums of EnCN,:M E iS SnCN,()=n n CN ∑m=1rhnm nm,,M i +SBn CN ∑■r hnm nm nk ,B ( ∑1-,Pak().(41)■■ ■m=1■ ■) ■■ ■■ ■∑,k=1■N τ2- +q x yq■nCN iC ,2 2 ,N ■■ ■■ ■■■■ ■i=1■■5.end for 6.Sort all the local maximums in the descending order as:E E E E ntotal)},(42) where ej() indicates the correspond i in equation (41),j Ke e(1 2n:,,,eK() ()… K{1 2ntotaltotal.= …1,2,,n 7.Compute the optimal amount of caching resource for MVNO n q e Sbest,= (1) .(43)8.end for 9.Output the local optimal solution QCN CN CN NCNnCN nbest best best best … }.(44)end:,,,{q q q 1,2,,

In the proposed Algorithm 4,we separate the virtualized hierarchical caching resource sharing problem into two parts and obtained the equilibrium solutions respectively as mentioned before.Performance of the virtualized hierarchical caching architecture and the proposed algorithms are evaluated in Section Ⅳ.

Algorithm 4.Iteration algorithm for global equilibrium solution of the hierarchical caching resource sharing problem.begin 1.Initialization:given the initial caching resource demands in RAN and CN of each MVNO■q q 1,1 1,M ■ QBS:■■⋮ ⋱ ⋮■(46),■… …■ ■q qN,1 ,NM ■■… },(47) and control accuracy ε1＞0 and ε1＞0.2.k1←1 3.Let Q Q QCN CN CN NCN :,,,{q q q 1,2,,ini is the initial caching resource demands in Algorithm 1.4.Run Algorithm 1 5.Update the BS cache demands by BS BSini= ,where QBSk1(48),where qnmq q a q= +best best∂best,,mBSnm nm nBSnm ,,,,∂Eqn nm best,k1,and qnmbest,are elements in sets QBSk1 and QBSbest.∑∑k k 6.while d1 1≥ε,where d q q 1= -1,,m-1)2NM= =1 1( nm n 1n m 7.Let Q Qini= k1BS BS Run Algorithm 1 8.k k 1 1← +1 9.Update the BS caching demands with equation (48)10.end while 11.Output the global optimal BS caching resource demands QBSk1.12.Run Algorithm 2 13.k2←1 14.Run Algorithm 3 15.Update the CN cache demands:best,(49),where qnCNk q q a q 2 = +best best∂∂nCNnCN nCN nCN nCN ,,,,Eqn,CNbestk best 2 and qnCN ,,are in sets QCNk2 and QCNbest.N 16.while d2 2≥ε,where d q q 2 2=∑n k k,2-1)2=1(nCN nCN -,16.Run Algorithm 3 17.k k 2 2← +1 18.Update the CN caching demands with equation (49)19.end while 20.Output the global optimal CN caching resource demands QCNk2 end

IV.SIMULATION RESULTS AND DISCUSSIONS

In this section,we use computer simulation method to evaluate the performance of our proposed hierarchical caching resource sharing scheme.For ease of illustration,we first consider a simple network scenario with two BS nodes and two MVNOs expect to share the hierarchical caching resource.Then we consider scenarios with multiple BS nodes and multiple MVNOs later.

The simulation parameters are set as follows.In price functions,we setx=0 andτ=1[20] ,respectively.Note that linear price function is a common assumption in an oligopoly market.To (avoid too small caching resource usage) make the simulation results easy to observe,we sety1=y2=0.2.We assume that the mean size of each content is 100Mb,the total number of contents owned by each MVNO is 1000,and the content popularity follows the Zipf-like distribution with the skewness factorβ=0.8 [27].Besides,we set the number of requests arriving at each BS of each MVNO to 2000.The backhaul cost and the link cost to Internet of transmitting 1Mbdata are 50 and 300 respectively.It is noted that some parameters are adjusted based on certain simulation scenarios.

The convergence of optimal caching resource usage over the iteration step is depicted in figure 2(a) and 2(b).We study the cache usage in BS nodes and the cache usage in the CN node.From Fig 2(a),we can observe that given the initial cache usage in BS nodes,the dynamic non-cooperative Cournot game of RANcaching resource sharing problem can get a Nash equilibrium after several iteration steps.As the price functionb(QBS) offered by InP increases,the optimal caching resource usage in the next iteration decrease.And the optimal caching resource usage in the next iteration step increase when the price function decreases.Similarly,the convergence of optimal caching resource usage at the CN node is shown in figure 2(b).

Figure 3,figure 4 and figure 5 show the effect factors of proposed virtualized hierarchical caching resource sharing problem.In figure 3 (a) and figure 3 (b),we set the number of requests belonging to MVNO 1 arriving at BS 1 as a variable and the other three numbers of requests as constants.It is obvious that the optimal cache usage of MVNO 1 at BS 1 increases with the increase of the corresponding number of requests,and the other three optimal caching resource usages decrease when the number of requests of MVNO 1 at BS 1 increases.In this case,when there are more requests,both two kinds of link costs increase,thus MVNO 1 prefers to buy more caching resource at BS 1.However,it causes rise of the price functionb(QBS),thus the other three optimal caching resource usages decrease.At the CN node,as the total number of requests of MVNO 1 arriving at the CN node increases,profit of caching more contents in the CN node for MVNO 1 increases.The optimal caching resource usage of MVNO 1 in the CN node increases.With increase of the price functionb(QCN),the optimal caching resource usage of MVNO 2 at the CN node decreases.Therefore,MVNO prefers more caching resource when more requests arrive.But this will cause the competition among MVNOs fiercer,and the caching demands of other MVNOs will decrease.In figure 4 (a) and figure 4(b),the relationship between mean content size of MVNO 1 and the optimal cache usage are depicted.It is obvious that with a larger mean size of contents,MVNO 1 prefers larger optimal caching demands both at BS nodes and at the CN node.And with higher price functions,other MVNOs prefer smaller caching spaces.Relationship between the total number of contents owned by MVNO 1 and the optimal cache usage are evaluated in figure 5 (a) and figure 5 (b).With more contents owned by MVNO 1,its optimal caching demands in BS nodes and CN node become smaller.This is because that hit ratio of one content decrease when number of contents increase.Thus the profit of caching decrease.

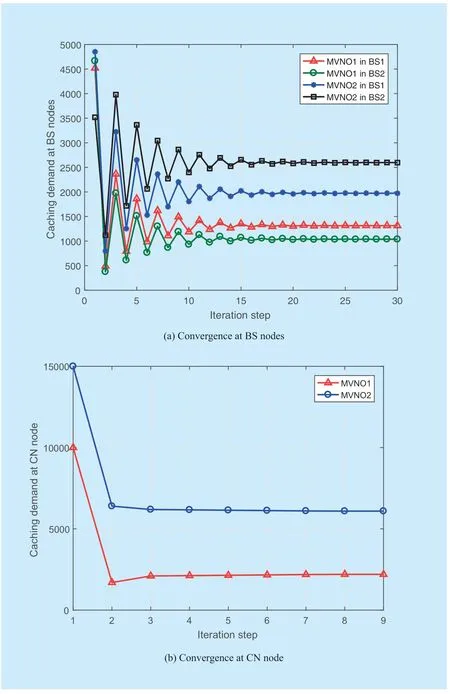
Fig.2.Convergence of the iteration algorithm.

So far,we have simulated the network scenario with two BS nodes and two MVNOs.In the following part,we will consider the network scenario with more two BS nodes and/or two MVNOs.In figure 6(a),we analyze the relationship between the number of BS nodes and the optimal cache usage.We use cache usage atBS1as the example.We can observe that when there are more BS nodes in the network,the optimal cache usage atBS1decrease.Whenτ=1 andx=0,as shown in equation (1),the price functionb(QBS) is a linear function of the sum of cache usages in all BS nodes.Therefore,the increase of the number of BS node will cause the competition fiercer,and the optimal cache usages at BS nodes decrease.On the contrary,the optimal cache usage at the CN node increase with the increase of number of BS nodes.This is because the decrease of cache usages at BS nodes makes elements in the sequencePnlarger,and that is to say,the profit of caching contents at the CN node increase.Thus the optimal cache usage rises at the CN node increase.

The relationship between number of MVNOs and the optimal cache usage is depicted in Figure Figure 6(b).To simplify the simulation,we set the number of BS nodes to 1 in simulation and use the cache usage of MVNO1 as the example.Similar to figure 6 (a),price functionsb(QBS) andb(QCN) are both linear functions of the sum of cache usages owned by all MVNOs in the case ofτ=1 andx=0.As a result,when more MVNOs are competing for caching resources,as the increase ofb(QBS) andb(QCN),both cache usages of MVNO 1 at the BS node and the CN node decrease.

Fig.3.Caching demand versus number of requests.

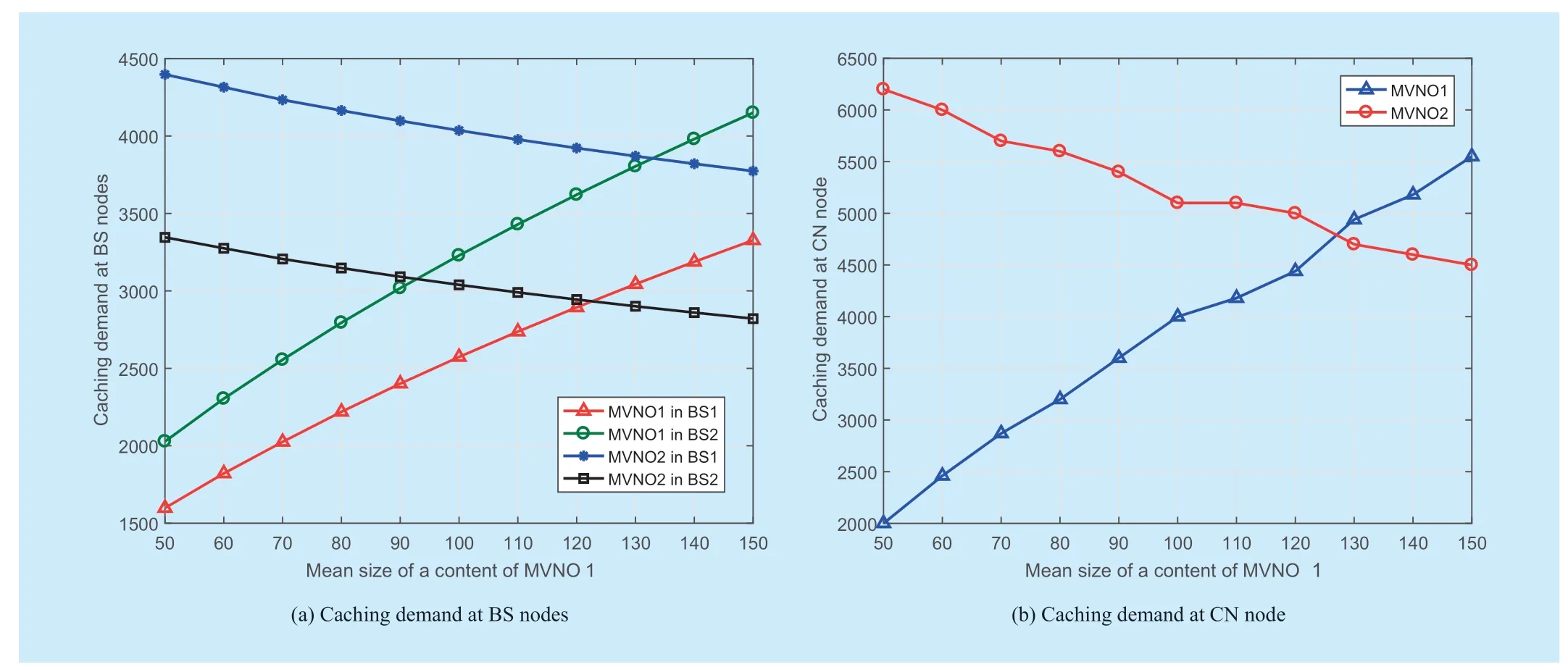
Fig.4.Caching demand versus mean content size.

In figure 7 (a) and figure 7 (b),we evaluate the variations of revenues for MVNOs when the cache usage is given.The revenue of MVNO 1 is still used as the example to show the performance.From the figures,we can observe that as it is proved in Theorem 1 and Theorem 3,both the revenue at BS node and the local maximal revenue at CN node are firstly monotonically increasing and then monotonically decreasing.Furthermore,the point with highest revenue is the optimal caching resource usage,which is shown in the figures.Through in comparison of the optimal cache usages when the number of MVNO is 2,3 and 4,we know that the optimal cache usages decrease both at BS node and CN node when the number of MVNO increases.It is the same with the conclusion observed from figure 6 (b).

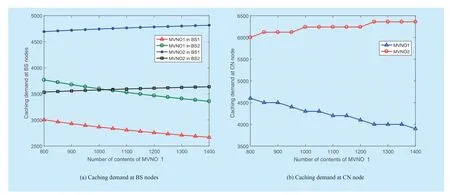
Fig.5.Caching demand versus number of contents.

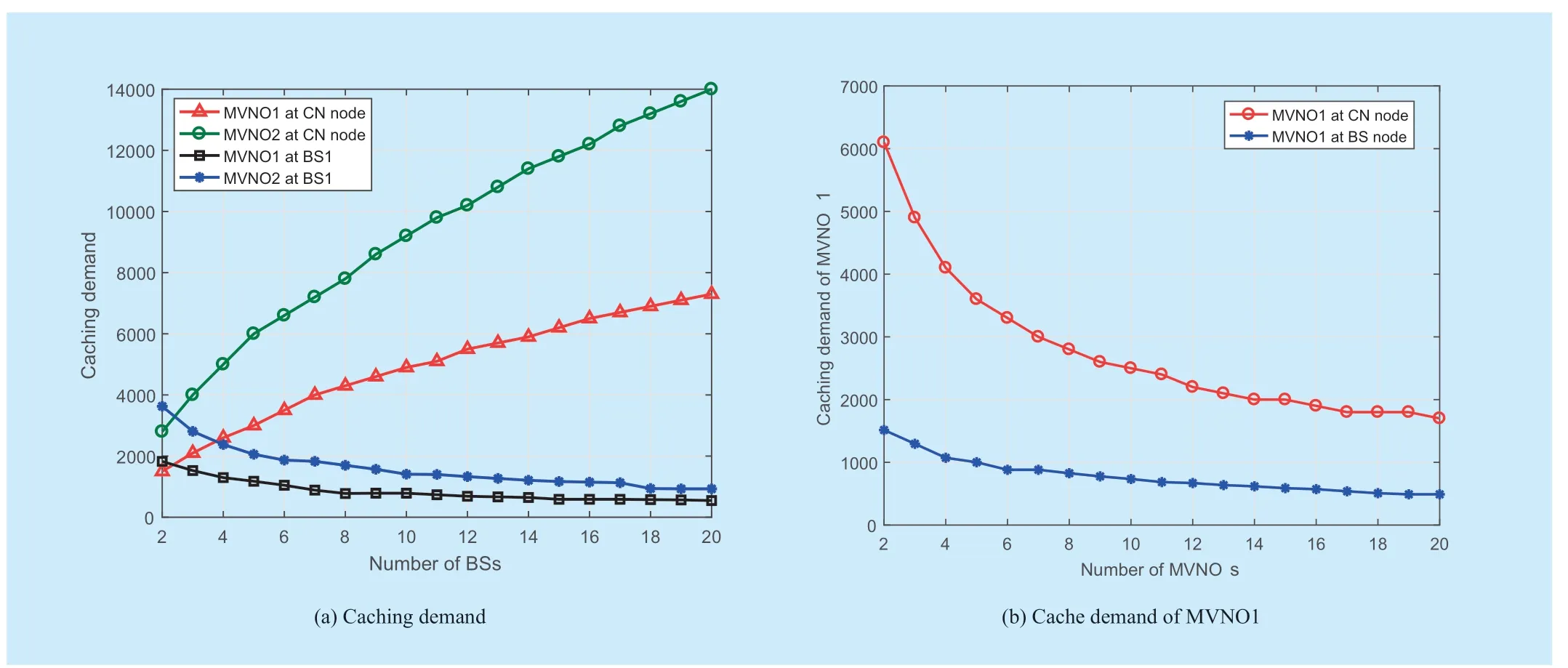
Fig.6.Caching demand versus number of BSs and MVNOs.

Fig.7.Revenues of MVNOs versus caching demand.

V.CONCLUSIONS AND FUTURE WORK

In this paper,we have studied the issues of hierarchical caching resource sharing for virtualized wireless network to maximum the profit of MVNOs.We have separated the caching resource sharing problem into two caching resource sharing problems in RAN and in CN.The RAN caching resource sharing problem is formulated as a dynamic Cournot game.Then an iteration algorithm based on the Newton-Raphson method has been given to obtain the local optimal solution.Next,we have proposed a request probability sorting algorithm and a discrete maximum value look up algorithm to obtain the local optimal solution for the CN caching resource sharing problem.An iteration algorithm for global equilibrium solution of the virtualized hierarchical caching resource sharing problem has been proposed.Simulation results have been presented to demonstrate the performance of the proposed scheme.

Since collaborative caching scenario isn’t in consideration of our proposed virtualized hierarchical caching resource sharing scheme,in our future work,we will consider the caching resource sharing scheme with collaborative caching among BS nodes and evaluate its performance.

ACKNOWLEDGEMENTS

This work was support by the Major National Science and Technology Projects (No.2018ZX03001019-003,2018ZX03001014-003).