周期性阵风流对通气航行体超空泡形态及流体动力特性影响

王 威， 王 聪， 李聪慧， 杜严峰

(哈尔滨工业大学 航天学院，哈尔滨 150001)

水下航行体借助通气超空泡的包裹，使得其表面的黏性阻力大幅度减小，航速得到突破性的提高[1]。采用主动通气的方式形成超空泡的关键是要向水下航行体的空化器后部注入空气或者其它不可冷凝气体，增大空泡内部的压力值，使得空泡尺度增加到足以包裹整个航行体表面。主动通气的方式由Reichard[2]最先提出，与单纯的依靠提高航速而生成的自然超空泡相比，通气超空泡对航行体的运动速度没有那样苛刻的要求，更加易于实现，而且通气量具有可控性，可以调节空泡对航行体表面的包裹范围，从而改变航行体的沾湿面积。Savchenko[3]提出了航行体在超空泡内部运动的四种模式，指出了沾湿区域可以为航行体提供升力，维持其纵平面运动平衡的作用。

目前对于航行体与空泡相互作用的研究多数是在稳定来流中改变航行体的攻角实现的，比如Lee等[4]在水洞实验段中安装了弧形的模型支撑机构，通过此机构连接的支撑杆控制航行体模型在水洞中做俯仰运动，实现航行体和超空泡的相互作用。Pan等[5]根据实验结果，设计了可以实现通气航行体俯仰运动的动态计算网格，通过数值计算的方式研究了通气超空泡内部压力变化特点。Yu等[6]利用数值计算方法，进一步研究了航行体俯仰运动时流体动力变化的特点。若是运动中的通气超空泡航行体遇到前方不稳定的来流，或是受到海面附近的波浪影响，其空泡形态往往会产生变化，影响到航行体表面的沾湿区域，进而改变航行体的流体动力，过大的来流扰动甚至可能造成空泡的溃灭。

针对这样的问题，明尼苏达大学的Arndt等[7]在水洞实验段中安装了由两片水翼组成的阵风发生器(Gust generator)，依靠上游水翼的往复摆动使下游流域产生周期性的阵风流动，研究了稳定流和阵风流作用下通气超空泡的生成和保持机制，并给出了通气率范围。Lee等[8-9]实验发现了阵风流作用下的通气超空泡形态变化特性，发现在阵风发生器的频率增大到一定程度时，通气空泡的长度将会缩短；Lee比较了前支撑和后支撑的方式对通气超空泡的影响，前支撑方式的支撑结构会在空泡上游造成扰动，使空泡壁面不光滑，而后支撑方式会抑制空泡变形，并且影响空泡尾部闭合。Sanabria等[10]实验研究了超空泡航行体的动力学建模与控制，结果表明阵风流作用下，航行体空化器受到的扰动可以忽略，但是尾翼因扰动产生的流体动力不可忽略。Karn等[11-12]实验研究了超空泡尾部的几种不同形式的闭合模式，研究了弗劳德数Fr和通气率系数Cq对这些闭合模式的影响，并分析了空泡内外压力变化和闭合转变的关系。Karn等[13]研究了阵风流作用下的通气率、流场速度、空化器尺度、流动不稳定性对通气超空泡产生和溃灭的影响，指出阵风流动会降低气泡的凝结效率，阵风振幅的增加导致空泡形成和溃灭的通气率略微单调增加。

目前研究阵风流对通气超空泡影响大多是利用水洞实验方式对单独空化器产生的通气超空泡进行的，主要是围绕空泡尺度及空泡尾部闭合机理展开的，受到实验条件的限制，阵风流场中的垂直速度变化采用单点测量的方式，难以捕捉整个流场垂直速度的变化特性，实验中的模型需要支撑结构固定，而支撑结构对空泡形态存在一定影响，并且阵风流作用下通气超空泡航行体的流体动力变化特性还没有相关研究涉及到。基于以上原因，采用数值模拟的方法，对阵风流作用下通气超空泡航行体的流体动力进行研究，不仅可以捕捉到整个阵风流场的垂直速度分布，而且可以避免支撑结构对空泡形态的影响，了解航行体的空泡形态变化细节，掌握航行体沾湿区域及流体动力的变化规律。

1 数学计算模型

1.1 控制方程

由于来流速度较低，流域的压力都远大于水的饱和蒸汽压，自然空化现象较弱，所以忽略自然空化的影响[14-15]，主动通气形成的超空泡内部基本被空气填满[16]。参照文献[17]对通气空泡流动的计算经验，本文采用VOF(Volume of fluid)两相流模型对通气超空泡进行数值模拟研究。

1.1.1 连续性方程

(1)

1.1.2 动量方程

(2)

1.1.3 体积分数方程

(3)

式中:αg为气体体积分数，αg+αl=1,αl为水体积分数，如果网格单元充满水，则αg=0；如果充满气体，则αg=1；如果网格单元中包含气体和水的分界面，则0<αg<1。

1.1.4 湍流方程

根据文献[18]对通气空化流动的计算方法，本文选择RNGk-ε湍流模型进行数值模拟研究，此模型是由Yakhot和Orzag提出的，它可以很好的处理高应变率和流线弯曲程度较大的流动，k和ε的输运方程如下

Gk+Gb-ρmε-YM+Sk,

(4)

(5)

1.2 验证计算模型及边界条件设置

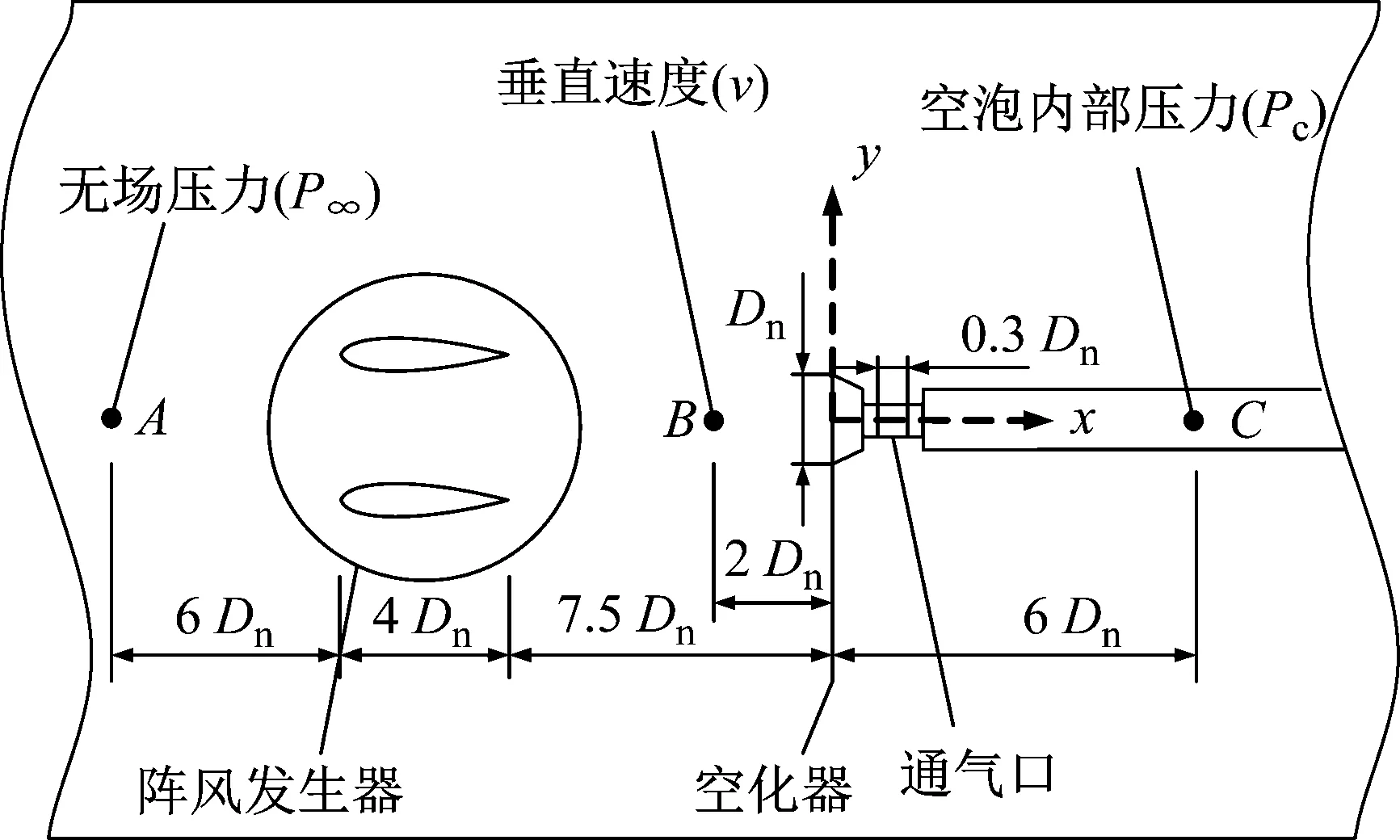
图1 空化器及阵风发生器的布置

整个计算流域如图2所示。水翼、空化器模型和支撑杆，采用壁面边界条件；流域左侧及流域四周边界均采用速度入口边界条件；流域右侧采用压力出口边界条件；通气口采用质量流量入口边界条件，通气率Cq=Q/(V∞D2)=0.15，其中Q是通气率，V∞为来流速度，D为模型最大截面直径(单独空化器时为空化器直径Dn)；阵风发生器外围的柱面将整个流域分为两个区域，这两个区域采用一对重合的圆柱交界面分隔，当阵风发生器摆动时，这对圆柱交界面之间相互滑动，而两个区域的网格并不发生变化。整个计算域采用六面体网格离散，数值计算开始前，采用不同网格尺度和时间步长进行网格独立性检测，确保模拟结果对网格密度和时间步长不再敏感。

图2 计算域及边界条件

1.3 航行体计算模型及边界条件设置

如图3所示，航行体模型由圆盘空化器、锥柱段弹身、圆柱形尾喷管组成。航行体模型的柱段直径D=40 mm，全长L=12D，其中圆盘空化器直径Dn=0.3D，航行体质心距离空化器6.5D,通气口距离空化器D/10，监测点的布置和图1的方式相同。航行体模型的计算域如图4所示，阵风发生器的水翼可以独自转动，模型后部没有支撑杆，边界条件设置与图2中的条件相同。

图3 计算模型

图4 航行体模型的计算域及边界条件

Fig.4 Computational domain and boundary conditions of vehicle

2 模型验证

在频率f=20 Hz，最大摆动角度θ0=±6°的条件下，监测点B的垂直速度计算结果和Lee的实验结果对比如图5所示。可以看出监测点B的垂直速度在阵风发生器的作用下呈现周期性变化，数值计算结果和实验结果有很好的一致性。Lee的研究结果表明监测点的垂直速度变化频率等于阵风发生器的摆动频率f，数值模拟得到的阵风流作用下通气超空泡形态变化和实验结果对比如表1所示。两者空泡形态变化的规律一致，充分验证本文数值模拟方法的有效性。

图5 监测点的垂直速度

表1 数值模拟结果和实验结果[8]对比

3 计算结果及分析

3.1 流域中波的特性

上游阵风发生器的摆动会在下游流场中将产生阵风流动，Lee通过水洞实验研究阵风发生器的频率和最大摆动角度对流域下游固定监测点B的最大垂直速度v的影响。受到实验条件的限制，实验中以单点测量不能够显示流场中不同位置的垂直速度分布情况，利用数值模拟方法可以很好地解决这一问题。在下游自空化器端面沿流动方向布置一条直线，用于监测流域中垂直速度的变化，具体布置如图6所示。

图6 流场监测线布置俯视图

Fig.6 The top view of the arrangement of the flow field monitoring line

在阵风发生器摆动几个周期以后，当水翼再次回到平衡位置时，流域中垂直速度的分布如图7和图8所示。

Lee的研究表明，流域中的波长λ=V∞/f，从图7可知，来流速度V∞相同时，阵风流的频率f越大，流域中的垂直速度的波峰之间距离越小，即波长变短，而垂直速度的峰值越高，即波幅越大。

从图8可知，阵风流的频率f相同时，来流速度V∞越大，流域的波长越大，且垂直速度的峰值也较高，即波幅越大。因为较大的来流速度可以把阵风发生器产生的扰动能量迅速的传递到下游流域，从而产生较大的波幅，而流速较小的情况，阵风发生器扰动的能量还没有及时传递到下游就已在水中因摩擦阻力的作用而快速衰减。

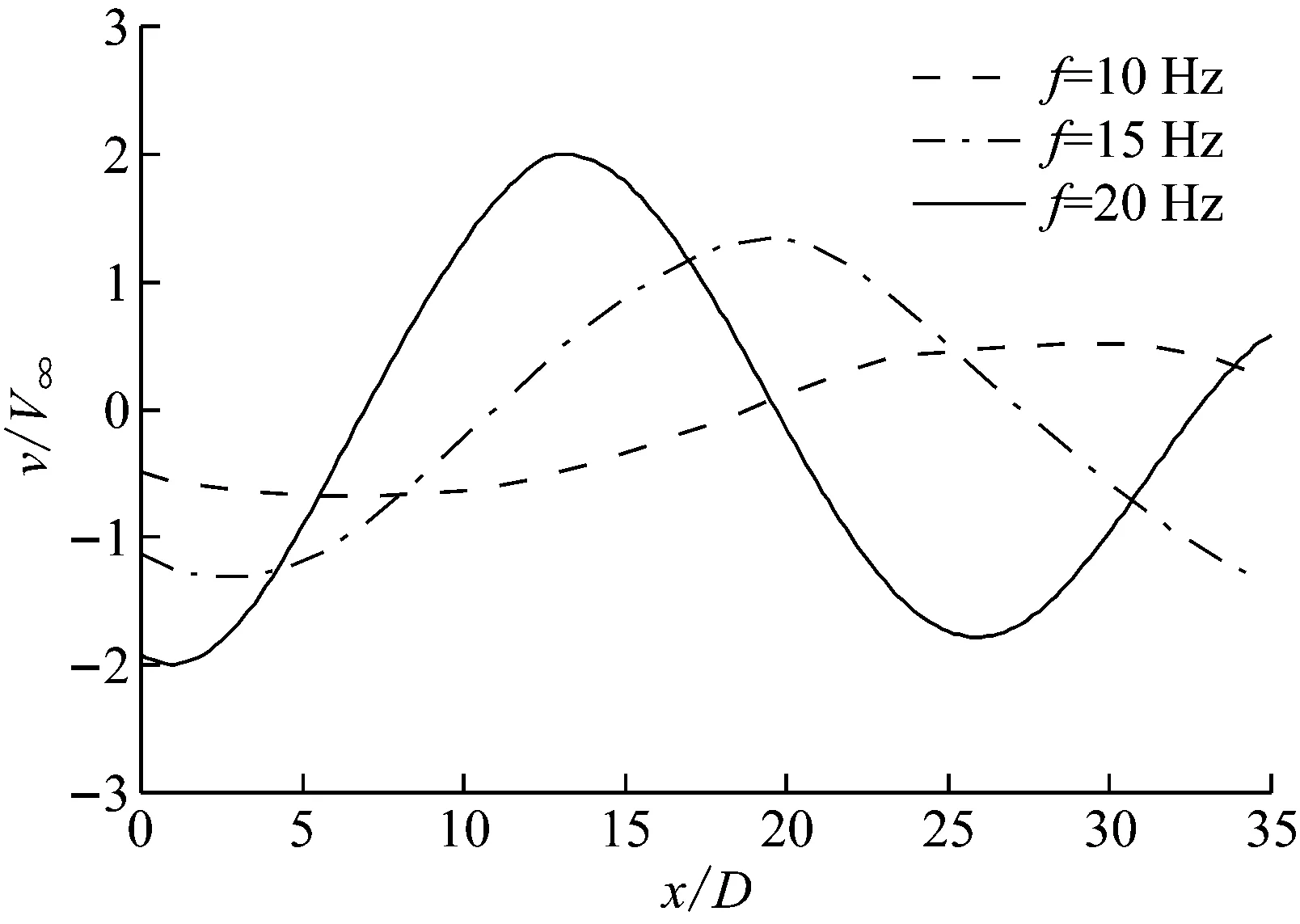
图7 不同阵风流频率下的垂直速度分布(V∞=20 m/s)

Fig.7 Vertical velocity distribution at different frequency of gust flow (V∞=20 m/s)

图8 不同来流速度下的垂直速度分布(f=20 Hz)

Fig.8 Vertical velocity distribution at different flow velocities (f=20 Hz)

Lee的研究发现短波对空泡长度的影响较大，从表1中也可以看出短波会加剧空泡的变形效果，为了研究阵风流作用下航行体流体动力变化，选择短波流动影响可以让通气超空泡变形，使航行体表面接触到流动介质，产生更大的流体动力变化。波长由阵风发生器摆动频率f和流速V∞的影响,从图8的讨论中可以发现给定的流速不宜过低;在低流速情况下，阵风发生器下游的波幅沿流动方向衰减较快，不适合研究阵风流动对通气超空泡航行体的影响。比较稳定流条件下不同流速的通气超空泡形态如表2所示。从表2可知,在来流速度较低的情况，通气航行体尾部已经形成了沾湿区域，这种条件不利于比较阵风流作用下形成沾湿区域的异同，而流速较高的情况，航行体模型没有接触到流动介质，因此在后面的计算中我们选择来流速度V∞=20 m/s，阵风发生器的频率f=20 Hz的工况进行研究。

3.2 流体动力特性

文中的阻力系数Cd、升力系数Cl、力矩系数Cm分别表示为

表2 稳定流条件下，不同流速下的空泡形态

Tab.2 The shape of cavities at different flow rates under stable flow conditions

流速V∞/(m·s-1)空泡形态

其中，Fx和Fy为x方向和y方向的阻力和升力；Mz为作用于航行体质心位置z方向的俯仰力矩；S为航行体柱段截面面积，L为航行体的长度。

阵风发生器摆动几个周期后，水翼再次回到平衡位置时，开始监测航行体的流体动力系数，无量纲时间T=t/T0，t为阵风发生器的摆动时间，T0为阵风流的周期。

三个周期内的流体动力变化结果如图9所示。阵风流动的作用下，航行体的流体动力系数出现了周期性变化，峰值左右的曲线并不对称，因为流场中重力影响使得阵风发生器向上和向下摆动时对航行体造成的扰动效果不同，从而影响到通气空泡形态及流体动力变化。另外的一个原因是文献[19]所提到的航行体附加质量力的作用，当阵风发生器高频率摆动时，流体对航行体作用的强度变大，航行体的附加质量力对流体动力的影响会增大，使航行体的流体动力曲线峰值向前偏移。为了观察一个周期内空泡形态的变化，比较图9中的9个特征时刻(a～i)的超空泡形态如表3所示。

图9 航行体的流体动力系数

表3 一周期内不同时刻的超空泡形态

Tab.3 The supercavitation shape at different time in a period

时刻通气超空泡形态及沾湿区域

从表3可知:①a时刻处于t=1T，航行体尾部的下表面出现沾湿区域，阻力系数不是最小值，升力系数为正值，升力作用点位于质心后方，所以力矩系数为正(力矩以使航行体逆时针转动为正)；②b时刻处于t=1.1T，随着超空泡形态的变化，航行体尾部的沾湿区域逐渐的消失，此时航行体的阻力系数最小，升力和力矩系数接近0，并在b时刻附近保持一段时间；③c时刻处于t=1.15T，此时航行体的上表面出现了一小部分沾湿区域，因此阻力系数有所回升，而升力系数开始向负值方向发展，由于升力的作用点位于航行体质心前部，所以力矩系数会向正方向有一个小波动，然后随着空泡形态的变化，沾湿区域逐渐扩大并沿航行体上表面向尾部位置移动，那么力矩系数向负值方向增大；④d时刻位于t=1.3T，此时航行体上表面的沾湿区域达到最大，阻力系数达到峰值，而升力和力矩系数达到负向最大值；⑤e时刻位于t=1.45T，此时航行体上表面的沾湿区域逐渐减小，因此流体动力系数也随之减小；⑥f时刻位于t=1.55T，此时航行体沾湿区域再次消失，阻力系数随之达到最小值，升力和力矩系数接近0，并在f时刻附近保持一段时间；⑦g时刻位于t=1.65T，此时航行体下表面开始出现沾湿区域，阻力系数逐渐回升，升力系数向正值方向增加，此时的升力作用点位于航行体质心的前部，所以力矩系数会向负方向有一个小波动，然后随着超空泡的形态变化，沾湿区域逐渐扩大并沿航行体下表面向尾部移动，因此升力系数向着正向增大；⑧h时刻位于t=1.75T，空泡形态因重力作用会上漂，航行体下表面的沾湿区域比下表面的沾湿区域大，所以此时的沾湿区域面积比d时刻大，阻力系数的峰值也比d时刻的情形要高，升力系数和力矩系数接近正向最大值，并且这个峰值要比航行体上表面沾湿的d时刻要大；⑨i时刻位于t=2T，此时刚好过了一个完整的周期，航行体尾部下表面形成沾湿区域，所以流体动力系数与a时刻相当。

3.3 航行体尾部沾湿区域的流体动力特性

通气超空泡航行体受到空泡的包裹，流体动力系数会大幅度减小，文献[3]指出了沾湿区域可以为航行体提供升力的作用，但是阵风流作用下，沾湿区域为航行体提供的流体动力的效果并不清楚，定义空化器阻力占总阻力的百分比为fcd；沾湿区域阻力占总阻力的百分比为fwd、升力占总升力的百分比为fwl；沾湿区域面积占航行体总面积的百分比为fA，时刻a～时刻i的这些比值情况如表4所示。

表4a～i时刻的空化器及沾湿区域的流体动力比例/%

Tab.4 The hydrodynamic ratio of cavitator and the wetted area in the working timea-i/%

时刻fcdfwdfwlfAa101.43.499.24.8b000c99.70.34.80.4d90.19.999.812.7e102.22.099.32.5f103.9000g98.02.022.54.3h86.113.999.919.3i101.03.299.14.0

从表4可知，空化器阻力比值fcd中，时刻(a、b、e、f、i)的数值达到100%以上，这是因为超空泡内部的回射流对航行体的前进方向有一定驱动作用，文中i时刻航行体表面的流线如图10所示。回射流作用使航行体总阻力减少，而空化器本身所受到的阻力是航行体阻力的主要部分，它受到回射流的影响较小，所以空化器所受到的阻力比例超过100%；而时刻d、时刻h的沾湿区域较大，使得空泡内部的回射流作用减弱，另外沾湿区域也分担了部分阻力，导致空化器所占的阻力比例有所减小。

图10 航行体表面回射流

沾湿区域阻力比值fwd中，时刻d、时刻h的沾湿区域阻力比例接近或超过10%，它们的沾湿区域面积占航行体表面积的12.7%和19.3%，可见沾湿区域面积对阻力的影响很大，沾湿区域的阻力比例随着沾湿区域面积的增大而增大，而其它时刻的沾湿区域面积较小，所以阻力比例也小。

沾湿区域升力比值fwl中，时刻(a、d、e、h、i)所占有的比例接近100%，例如i的沾湿区域面积只占有航行体总面积的4%，但却提供了99.1%的升力，而c和g的沾湿区域占航行体总面积的比例虽小，但升力却占有总升力的比例较大，可见沾湿区域对航行体尾部升力的影响很大。

3.4 沾湿区域的压力分布特性

从上面的分析可以发现，沾湿区域的升力占有总升力的比率较大，以g时刻为例，其沾湿区域位于航行体的下表面，分析该时刻g的沾湿区域的特性如图11所示。

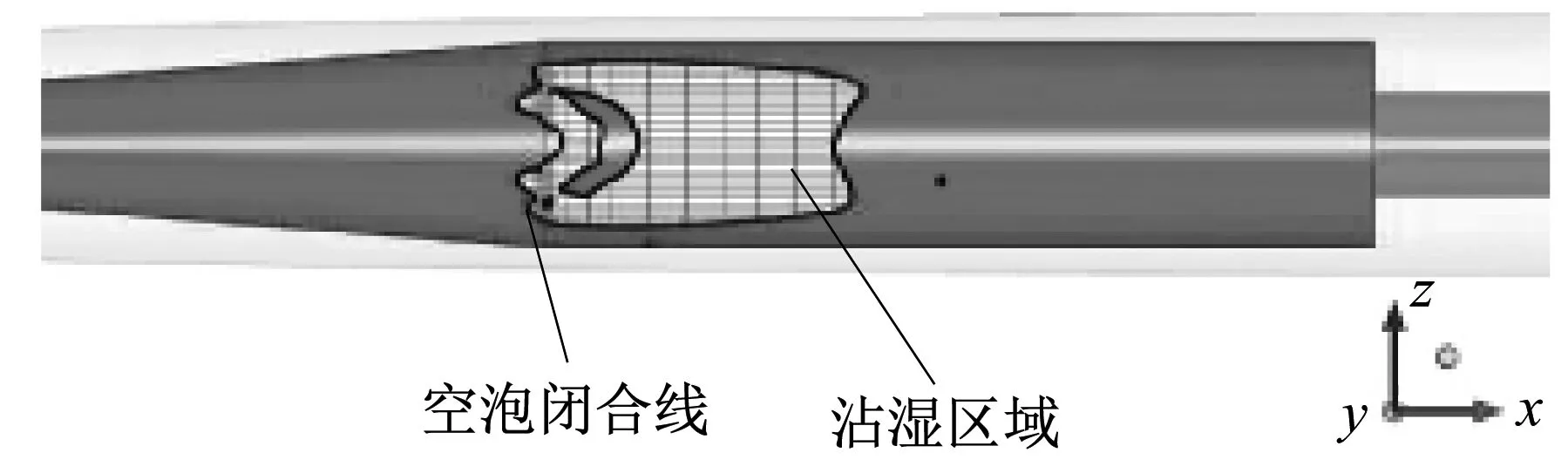
(a) 沾湿区域位置

(b) 空泡内部流线图

(c) 沾湿区域压力云图

图11(a)中标注了沾湿区域的具体位置并用网格线表示，从图11(b)可知,空泡内部的流线分布特点，在沾湿区域附近的流速很高，接近远场来流的速度V∞，高速区域基本处在沾湿区域的附近，因沾湿区域脱离了空泡的包裹直接与外部的流动介质接触，所以在沾湿区域的边缘形成了速度很高的回射流，而远离沾湿区域的位置回射流减弱；从图11(c)可知,模型表面沾湿区域的最大压力出现在沾湿区域的前部位置，处于空泡闭合线左侧，流场中的回射流使该位置的压力增大，而且该压力峰值比沾湿区域的压力还大。

如果航行体被整个空泡包裹，表面没有出现沾湿区域的工况f中航行体表面的压力处于35～36 kPa，而时刻g出现了沾湿区域，其压力最大值达到了61 kPa，正是这样的高压使得沾湿区域的面积虽小，但却可以给航行体的表面带来很大的压力，进而影响航行体的流体动力变化。

4 结 论

本文使用动态网格技术数值模拟研究了周期性阵风流作用下通气超空泡航行体的空泡形态及流体动力系数的变化过程，获得的主要结论如下：

(1) 周期性阵风流作用下，通气超空泡航行体的空泡形态及流体动力呈现周期性变化，阻力和升力系数随着沾湿区域的面积的增加而增大；一个周期内，沾湿区域相对于航行体质心的位置变化会使力矩系数出现两次小幅度波动。

(2) 周期性阵风流作用下，空化器阻力占航行体总阻力的比例较大；沾湿区域阻力占航行体总阻力的比例随着沾湿区域面积增大而增加，沾湿区域升力占航行体总升力的比例较大。

(3) 沾湿区域前端的空泡闭合线附近，受到回射流影响出现了高压区，使得沾湿区域的面积虽小，却可以为航行体提供很大的升力。