竞争失效条件下的装备选择性维修优化方法

逯 程，徐廷学，李启超，朱桂芳

（1.海军航空大学 岸防兵学院，烟台 264001；2.中国人民解放军91206部队，青岛 266100；3.火箭军士官学校，青州 262500）

由于目前海军舰船执行战备巡逻、值班、训练及演习等任务日益增多，武器装备的维修保障工作也面临新的挑战。为了科学合理地安排维修保障活动，确保装备以良好的状态顺利完成各项任务，维护人员会在任务间隙对武器装备进行必需的检测和维护工作。但是，考虑到有限的维修器材、备件、经费和时间等条件，不可能使所有装备都得到系统而完善的检修，此时决策者往往需要综合权衡维修资源消耗与目标任务要求和维修后装备性能的关系，选择装备中一部分可能影响下一阶段任务执行效果的关键部件进行维修，即选择性维修（Selective Maintenance）决策。

选择性维修理论[1]自提出以来，便一直是维修决策领域的研究热点[2-7]。有关不同情况下的选择性维修决策优化问题已有不少研究成果，有面向多种对象采用不同维修方式的选择性维修模型[8-9]、考虑多种资源约束的维修活动优化研究[10-11]、选择性维修模型智能求解算法研究[12-13]及面向连续多阶段任务的选择性维修优化决策问题[14-15]、考虑经济相关性的串并联系统选择性维修建模[16]等等相关研究。

近些年，针对复杂多状态系统的选择性维修问题，Chen[17]等首先以维修成本为目标对多状态系统的选择性维修模型展开了研究，假设串并联系统的部件为K+1个状态，通过状态转移概率矩阵和任务成功率的相关限制条件建立了选择性维修模型；Liu[18]等在多状态系统可靠性理论的基础上构建以维修费用为目标的选择性维修模型，并利用遗传算法进行求解；Zuo团队基于 Markov与通用生成函数理论构建了多状态多部件系统的选择性维修模型，并探讨了多种相关性因素对维修决策结果的影响[19-22]。

虽然上述基于多状态系统理论的选择性维修问题研究取得了一定进展，但在以下几个方面还有待继续深入探讨：1）考虑到导弹随舰船在海上执行任务过程中受到振动、冲击及负载等外部环境及其它不确定性因素的影响，装备的性能状态除了自然退化以外，还面临着随机冲击等突发失效与自然退化二者相关竞争失效(Competing Failure,CF)的共同作用[23-24]，现有的选择性维修决策模型并没有考虑竞争失效的因素及随机竞争失效事件（Random Competing Failure,RCF）对任务成功概率评估的影响[25]；2）现有文献的研究对象一般为单一多状态系统，而部队日常训练及保障任务的开展大多需要一定数量的装备共同参与完成，即针对集群装备研究其在任务间隙的选择性维修问题对决策者更具参考意义与价值；3）大多数文献都以维修费用作为约束条件或优化目标，但是在部队实际的装备保障工作中，经济成本并不是考虑的重点，如何在现有的备件资源条件下按时完成维修任务才是关键；4）现有研究大多假设系统及任务参数为确定值，然而在实际部队背景下，由于战备巡逻等任务密集灵活，任务命令的到达具有很强的随机性，加上任务环境复杂多变及其它未知因素的影响，任务进程和装备系统参数往往存在模糊特性。

基于以上分析，本文重点研究当装备参数、任务持续时间及需求、随机竞争失效事件到达率及其导致的状态转移概率均为模糊数，且任务间隔时间为随机变量时，针对集群装备的选择性维修建模问题，并分析模糊RCF与相关任务参数对维修优化方案的影响，为决策者科学有效地安排选择性维修活动提供理论依据与支持。

1 问题描述

某型装备为模糊多状态系统，假设其由m个多状态子系统组成，子系统均采用模块化设计。子系统共有qj+1个状态，0表示故障失效状态，qj表示全新状态，1,2,,qj-1为中间退化状态，各状态性能为利用表示子系统j在时刻t的模糊状态性能，且其处于各状态性能的模糊概率为系统的状态性能则由其各个子系统的组成结构和状态性能决定，若系统可能存在个状态，其在时刻t的模糊状态性能表示为为模糊多状态系统的结构函数，系统的各模糊状态性能表示为且同样系统处于各状态的模糊概率为

某舰基导弹装备系统在完成海上战备护航与巡逻训练等任务后，通常需要返回技术阵地进行状态检测和维修保障等工作，在下一任务开始前的任务间隔期内实施装备维修活动，以满足下个任务的性能要求，装备任务剖面如图1所示。鉴于部队维修保障的实际情况，在有限的备件资源和维修时间条件下只能对故障或退化装备的部分关键模块进行选择性维修。另外，由于任务的不确定性，任务间隔期Tb为随机变量，下一阶段执行任务的时间也存在模糊特性。装备在海上执行任务过程中，由于随机冲击载荷及振动等事件的影响，会面临自然退化和相关竞争失效导致的状态转移，随机竞争失效事件以一定的分布产生，并以一定的概率造成子系统间的状态转移，其到达率和状态转移概率均为模糊数。维修决策者需要针对某批集群舰基装备统筹考虑有限的备件资源、任务间隔时间、持续时间、随机竞争失效的模糊特性及任务需求等要素，优化维修决策方案，实现最大化装备任务成功概率的目标。

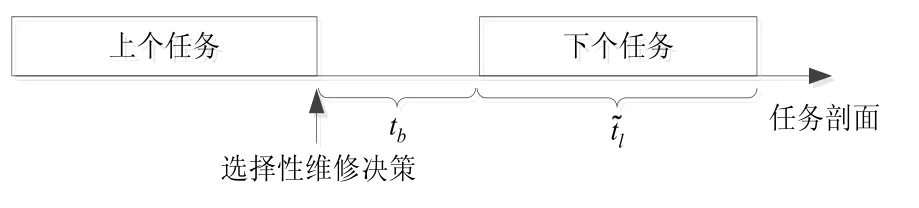
图1 任务剖面Fig.1 Task section

为便于研究分析，并结合部队实际，本文做如下假设：

① 任务结束后会进行装备综合测试，维修工作开始前各装备子系统模块状态已知；

② 装备维修工作仅在两个相继任务之间的维修间隔期内开展，任务过程中不进行维修；

③ 只有装备群内所有装备完成相应维修方案后，才能开始下一任务阶段；

④ 对各子系统模块采用不同维修方法对应恢复的性能状态不同，仅考虑维修时间和库存备件两种维修资源，各维修方法的时间和备件消耗已知；

⑤ 部件的状态转移由自然退化和随机竞争失效两部分原因造成，自然退化符合齐次 Markov过程，竞争失效事件的发生符合泊松过程。

2 维修方式及维修资源需求建模

假设模块j维修前后的状态分别为Hj和Yj，则装备i对应的维修方案为考虑非完美维修的情况，模块j的维修方法可以分为以下几类：

1）不修。不采取任何维修活动的情况下模块状态保持不变，即Hj=Yj。

2）非完美维修。非完美维修是部队基层保障单位常见的一种维修方式，包括参数调试、擦拭上油及三防处理等工作，模块状态能恢复到全新状态qj与当前状态Hj之间的中间状态，即Hj＜Yj＜qj；

3）完美维修。完美维修包括模块预防性更换和故障性更换工作，可以将其恢复到全新状态，即Yj=qj。

这里用二态变量Vij表示是否对装备i的模块j进行维修，Vij=0表示不修，Vij=1表示维修，则该模块维修活动可以表示为：

在基层保障工作中，维修时间分为固定时间和可变时间两部分，固定时间包括装备技术准备和综合测试等工作所需要的时间，可变时间包括改善模块状态所需要的时间，其具体数值依赖于相应调试及更换等维修方法。某类关键模块的备件消耗取决于该模块是否进行预防性或修复性更换维修。

对于m个多状态子系统模块构成的装备i来说，其维修方案可以表示为，则集群装备的维修方案为为装备数目，总的维修时间和备件消耗量分别为：

3 模糊随机竞争失效条件下集群装备选择性维修决策建模

3.1 模糊集理论

设给定一个论域U，通过一个隶属度函数：U→[0 ,1]可以确定一个模糊子集，任意值x的隶属度(x)的大小表示其对模糊子集的从属程度。= ｛x|(x)≥α｝ 表示模糊子集的α( 0 ≤α≤1)水平截集，其区间表达形式为

常用的三角模糊数可以表示为 (a,b,c)，其隶属度函数及α( 0 ≤α≤1)水平截集（如图2所示）分别表示为：

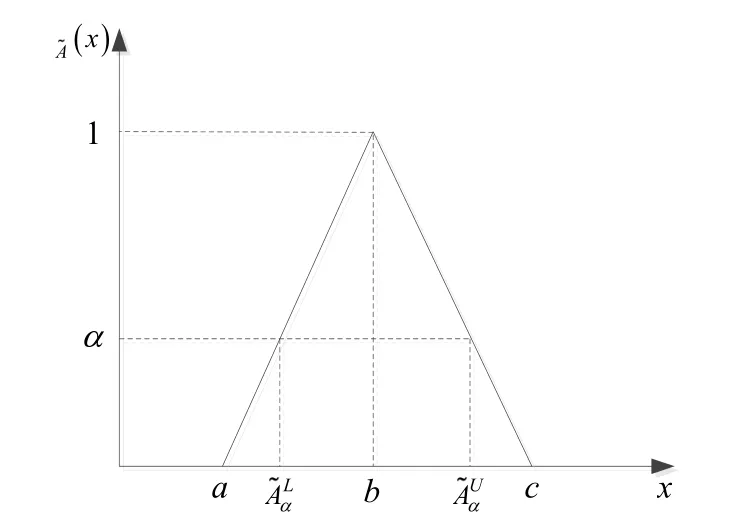
图2 三角模糊数的α水平截集Fig.2 The α-cut level set of triangular fuzzy numbers

3.2 模糊多状态子系统状态分布

为便于分析，这里首先从单个装备子系统模块入手。考虑到随机竞争失效事件的发生服从泊松过程，当相关参数具有模糊特性时，子系统模块退化过程中的模糊状态分布采用模糊Markov过程[26]进行建模。

当某装备按照给定的方案进行维修后，子系统的状态即确定，在仅考虑自然退化的情况下，子系统j在下个任务的状态转移率矩阵为：

考虑由随机竞争失效事件导致的子系统状态转移情况，如图3所示，令RCF事件的到达率为，该情况下子系统j从状态v到状态k的模糊状态概率表示为，且

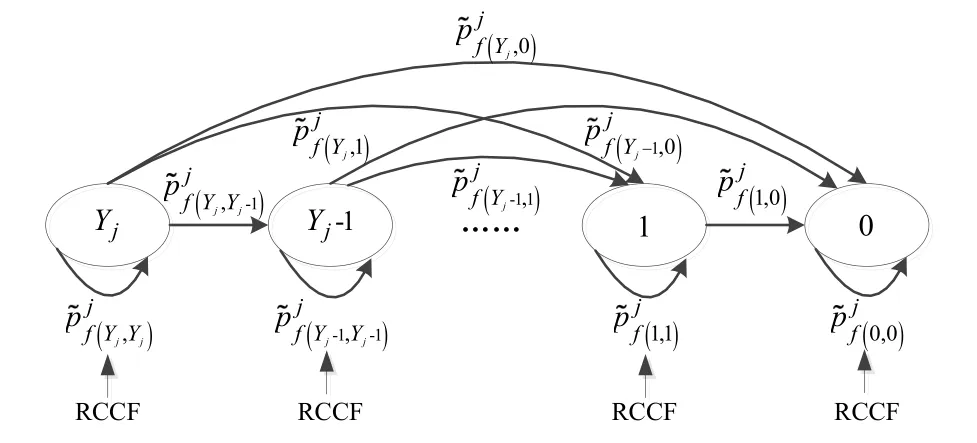
图3 随机竞争失效导致的状态转移Fig.3 State transfer caused by competing causes of failure

下面由子系统j在t时刻处于状态v的模糊概率推导出下个任务结束后处于状态k的概率分为以下两种情况讨论：

情况1：状态保持不变。

在此情况下，经过Δt后子系统状态未发生转移，即状态k=v。当只分析自然退化造成的原因时，Δt内子系统状态保持不变的概率为代表模块各状态。进一步考虑随机竞争失效事件的影响时，又可分为以下两种原因：Δt内未发生 RCF事件的概率为1-Δt；发生RCF事件但保持原状态的概率为综合分析自然退化和 RCF事件的共同影响，模块j在Δt时间内状态保持不变的概率为：

情况2：由其它状态转移到状态k。

模块j在Δt内发生状态转移的原因仍然要综合分析自然退化和 RCF事件的共同影响。仅考虑自然退化造成的状态转移概率为若状态转移由 R C F事件造成，则概率为：因此，模块j在Δt内由其它状态转移到状态k的概率为：

其中，v=k+ 1,,Yj。

综合以上两种情况，模块j在t+ Δt时刻处于状态k的模糊概率为：

对式(9)求导得：

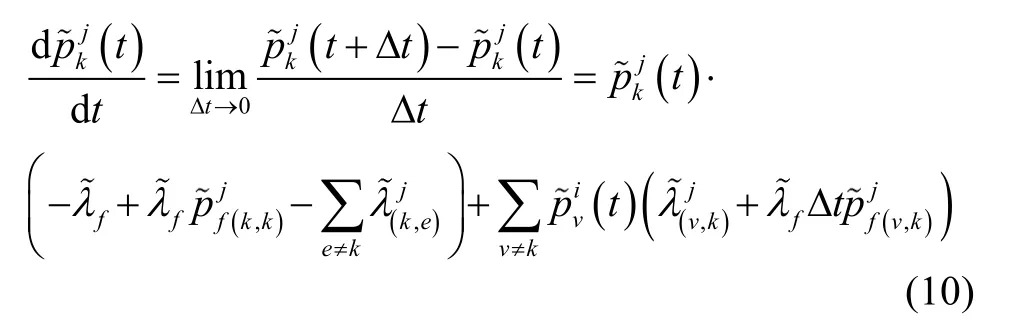
Kolmogorov微分方程组即：

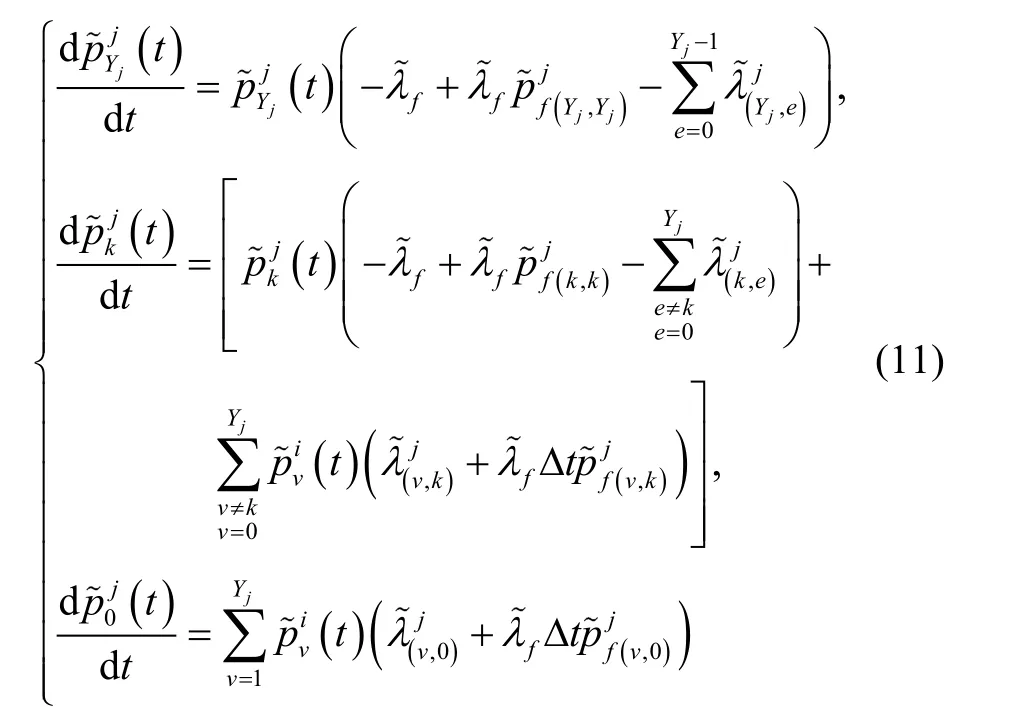
其中，0 ＜k＜Yj，模块j在进行非完美维修或更换备件后的初始条件为：

进一步对方程组进行Laplace变换得：

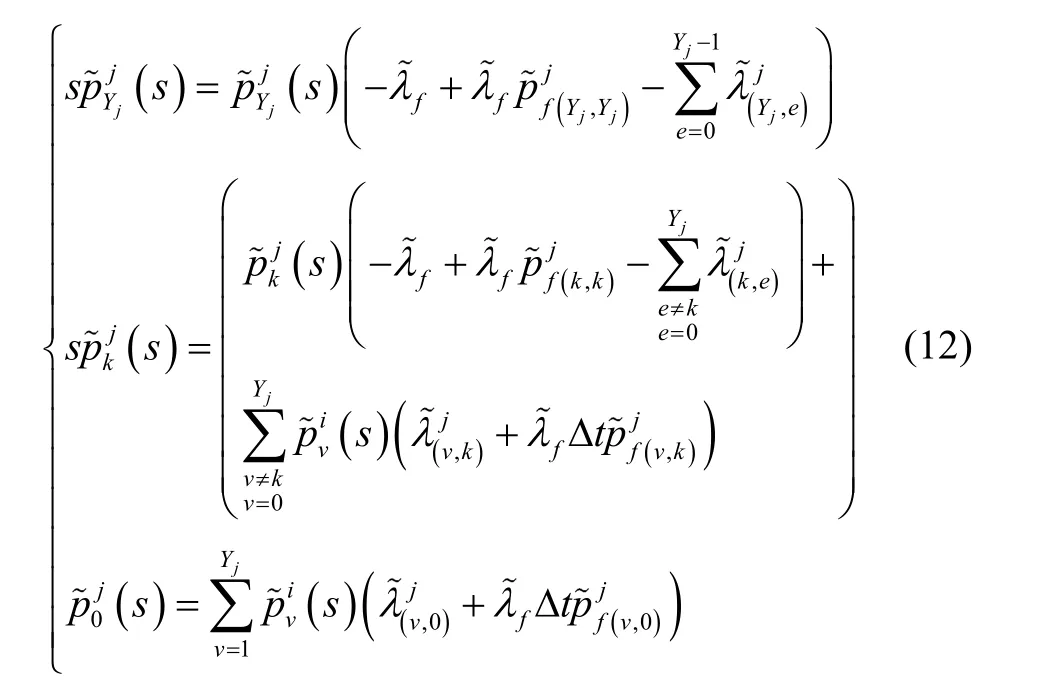
模块j在任务模糊持续时间内处于状态k的概率即表示为，利用模糊通用生成函数法[27](Fuzzy Universal Generating Function,FUGF)就可以得到模块j在任务结束时的状态分布函数：

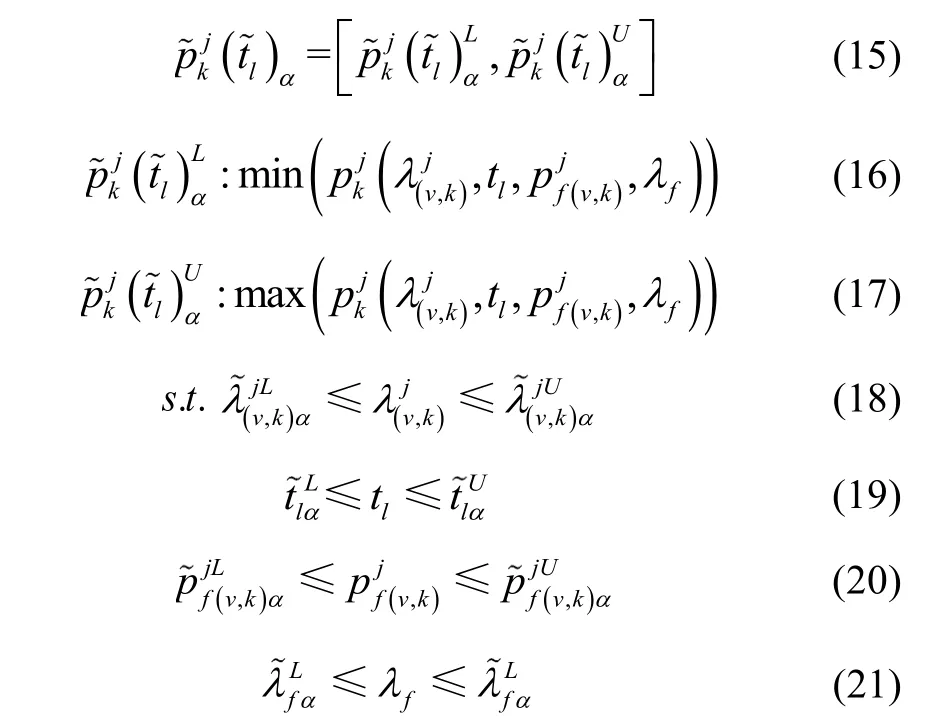
3.3 多状态装备系统模糊状态分布

根据FUGF理论，利用一个模糊合成因子表示装备系统所有m个子系统模块在任务完成后的联合状态分布：

其中，φ（•）为装备结构函数，k为任务结束时的装备状态，为状态k对应的性能等级和概率，同样通过非线性规划的方法得到二者的α水平截集：

3.4 集群装备模糊任务成功概率评估

考虑到部队的实际情况，作战任务往往具有较强的灵活随机性[28]，假设任务间隔期Tb为一服从概率密度函数f(Tb)的随机变量，这里定义任务成功概率时，不仅要求集群装备满足一定比例的任务性能指标，还要考虑维修方案能否在间隔期内实施。因此，对于给定的维修方案L，其所有装备的总维修时间与任务间隔时间的大小存在多种可能，若要求维修活动在Tb内完成，即t（L） ≤Tb，其概率为：

下面进一步分析单一装备i的任务模糊满足概率，假设下个任务的性能需求为w，则装备满足任务要求概率的α水平截集为：

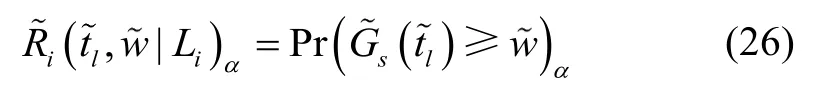
这里利用相对基数[29](Relative Cardinality)法对式(26)进行计算，令考虑到α水平截集在不同取值下模糊区间的变化，本节对其进行改进计算：

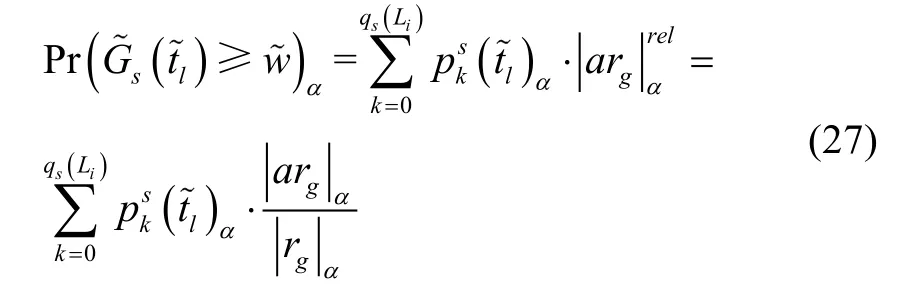
同理，装备i的任务满足率α水平截集区间依然采用参数规划求解。

下面分析集群装备的任务要求，假设该批装备在任务结束时至少有数量M的装备达到性能要求w，则装备群满足下个任务要求概率的α水平截集为：

其中，N为装备数量，为满足性能需求的第j种装备序号组合，为剩余不满足要求的装备。

综上所述，根据式(25)(30)，综合考虑任务间隔期内的维修时间和执行任务的性能需求两方面的因素，当给定维修方案L后，集群装备的模糊任务成功概率为：

3.5 选择性维修决策建模

考虑到实战背景下的任务要求，针对下一阶段任务的随机不确定性特点，部队决策者通常希望在现有的维修备件资源的约束条件下，在维修间隔期内完成所有的维修活动，并使装备满足任务要求，从而实现任务成功概率最大的目标。因此，通过建立选择性维修决策模型，可以得到任务成功概率最大时的最优维修方案，决策模型如下：

式(32)表示决策目标为最大化任务成功概率；Bj表示j类备件的库存量，式(33)即备件约束条件；式(34)表示维修前后子系统模块的状态约束关系；维修方案为需要优化的变量，其中

3.6 基于Memetic算法的模型求解

根据3.5节建立的模型可知，选择性维修决策模型的求解是一个复杂的非线性规划问题，当针对集群装备的维修方案进行寻优时，由于可行解的空间较大，而传统枚举搜索法求解效率又很低，因此本文利用Memetic智能算法进行模型的求解。

Memetic算法[30]是一种基于全局搜索和个体搜索相结合的混合算法，这里全局搜索策略采用遗传算法，产生每一代种群后，利用禁忌搜索算法进行局部寻优。首先基于维修后的状态进行染色体编码，则种群个体对应的可行解为：

步骤1按照设定的种群个体数NR随机生成初始可行解，利用禁忌搜索算法寻求局部最优解，并作为当前可行解L0；

步骤2进行交叉和变异操作。这里采用一点交叉法，直至得到可行解或达到循环次数为止；随后以一定概率进行变异，若变异后的父染色体更优，则进行局部搜索后完成替代，直至得到可行解或达到循环次数为止；

步骤3计算染色体适应度

步骤4利用赌轮盘法选择染色体，若染色体最优解优于L0，则替代L0，否则从步骤1重新循环直至达到迭代次数为止。

局部搜索策略如下：

步骤1禁忌搜索的起始当前解和最优解设置为计算的染色体值，并置空初始禁忌列表；

步骤2改变当前解的每一位状态值，在邻域解中剔除不符合约束条件与禁忌列表中相同操作的解，选出目标函数最大值作为当前解，并将相应禁忌对象加入禁忌列表；

步骤3用更大目标函数的当前解替代最优解；

步骤4重复第2步和第3步，直到迭代结束，并用最优解替代原染色体。

4 案例分析

4.1 选择性维修模型求解

以某型捷联惯性导航系统为研究对象，进行分析作为导弹制导控制系统的重要组成部分，捷联惯导系统可在岸基或舰载条件下完成初始对准，在导弹飞行中自主导航，实时向综控机发送导弹的姿态角、角速率、位置和速度等信息，用于导弹控制。

通过研究某综保基地近5年海外护航及战备巡逻等任务的维修保障记录发电，捷联惯导系统的状态退化及故障情况主要集中在三轴激光陀螺仪、石英挠性加速度计及直流电源分机子系统。为便于分析，本节将捷联惯导系统简化为三个关键子系统功能模块进行研究，分别编号为陀螺仪模块1、加速度计模块2及电源模块3。

已知某批次导弹共10枚，在上一任务结束后从舰上返回技术阵地进行惯导单元测试，测试结果分为完好、堪用、拟故障、故障4个状态等级，依次表示为状态3～状态0，各装备子系统模块维修前状态及模糊性能如表1及表2所示。备件库存量及维修时间等维修资源需求见表3。

假设任务间隔时间服从指数分布，参数为λb=0.15/天，任务持续时间为tl=(7 .5,8,9)月，下个任务的性能目标为至少 80%的装备满足性能需求w=(70,80,85)。执行任务过程中，装备会遭受自然退化及RCF事件，RCF事件的到达率为λf=(4,5,6)/月，分别考虑自然退化和 RCF事件的子系统模块模糊状态转移率如表4和表5所示。

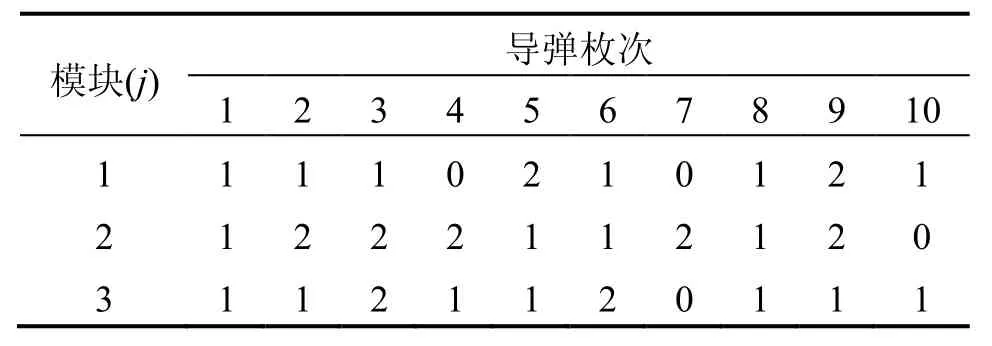
表1 维修前装备模块状态Tab.1 Equipment subsystem state before maintenance

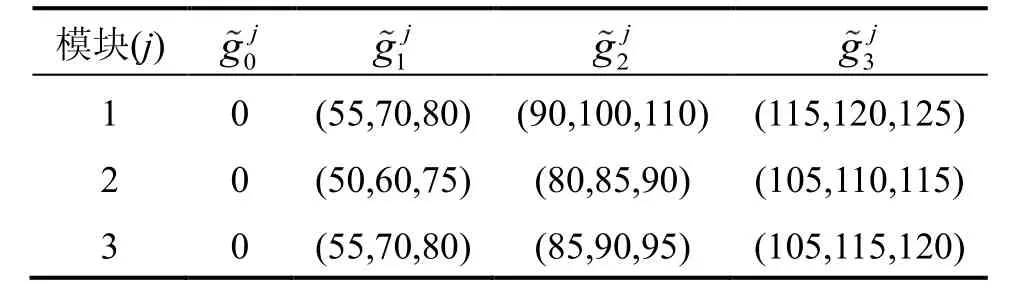
表2 模块状态对应模糊性能Tab.2 The fuzzy performance of the sub-system state

表3 维修资源需求Tab.3 Maintenance resource requirements

表4 自然退化条件下的模块状态转移率（月）Tab.4 State transition rate of modules under natural degradation (month)

表5 RCF事件导致的模糊状态转移概率Tab.5 Fuzzy state transition probability caused by RCF event

根据维修前各装备子系统模块的状态情况，利用Memetic智能算法进行模型求解，排除一些不合理的维修方案，如对故障模块不予修复，而对处于退化状态的模块进行换件等维修方案。这里的维修方案用各模块维修后的状态表示，数字3～0依次对应完好、堪用、拟故障、故障4个状态等级。在所有可行解中得到最优的维修方案，其维修方式、时间及模糊成功概率如表6所示。

将维修方案依然用维修后子系统模块的状态表示。在仿真过程中计算发现，在模糊参数下计算得到的许多可行方案的任务成功概率值并不是标准的三角模糊数。当α较大时，由于某些维修方案耗时超过任务间隔时间或无法达到任务需求目标，出现了任务成功概率等于0的情况。另外，当α=1时，在维修方案的隶属度等于1的情况下，还出现任务成功概率的跳变，这是因为方案满足维修时间和任务需求的这两个概率有可能跳变为1。

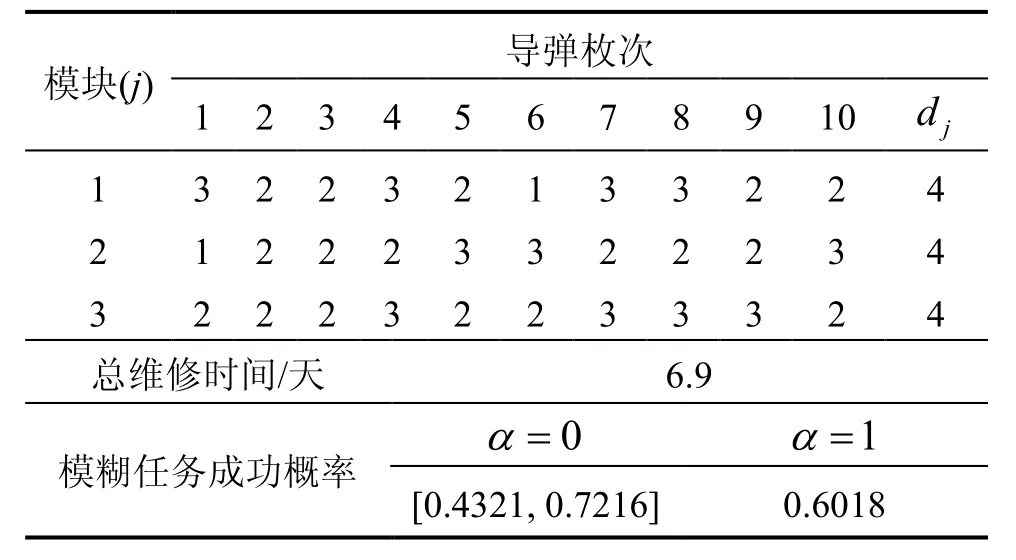
表6 最优维修方案Tab.6 Optimal maintenance scheme

综合所有可行解最终得出，表6所示维修方案的任务成功概率最大，当α=1时，为确定值0.6018，此时总维修时间为6.9天，三类子系统模块分别消耗4件。

4.2 λb对选择性维修决策结果的影响

对于下一阶段的随机不确定性任务，参数λb的大小会直接影响任务间隔时间的长短。从理论上出发，对于某一维修方案，λb越大，则任务间隔时间越小，维修时间越紧张，任务的成功概率会因此降低。为了进一步分析λb对选择性维修决策结果的影响，分别对不同λb值下维修方案的任务成功概率变化情况进行了仿真，α=1时的结果如图4所示。

图4 λb对任务成功概率的影响Fig.4 The effect of parameter λbon the mission success probability

由图4可以看出，对于给定的维修方案，任务成功概率会随参数λb的增大而减小，这也与前文的理论分析一致，这也从侧面验证了模型的有效性；另外，当λb的变化范围离开某一区间，还会影响到选择性维修决策的结果，导致维修方案发生变化。

4.3 随机竞争失效对选择性维修决策的影响

进一步分析RCF事件对决策结果的影响，在建模过程中不考虑随机竞争失效因素，通过对可行方案的模糊成功概率仿真计算可得，当α=1时，表6中方案仍为最优维修方案，任务成功概率为 0.7223，大于0.6018（表6中维修方案）；当0≤α＜1时，在不考虑隶属度为1的情况下，最优维修方案发生了变化，如表7所示，此时对应的任务成功概率最大。

由此可见，随机竞争失效不仅会影响任务成功概率评估值，还会直接影响最终的维修决策结果。所以，在选择性维修决策建模的过程中将装备 RCF事件的影响考虑在内是必要的。

表7 不考虑RCF时的维修方案Tab.7 Maintenance scheme without considering the RCF

5 结 论

本文考虑部队实际任务间隔的随机特性，在多状态系统参数、任务参数及随机竞争失效参数均为模糊数的情况下，研究了竞争失效条件下集群装备的选择性维修决策问题。文中建立了针对装备群的任务成功概率评估模型，并以其为目标函数，在备件资源的限制下利用 Memetic算法计算得到可行的最优维修方案，有效解决了模糊随机竞争条件下的面向随机不确定任务的多装备选择性维修优化问题。同时，分析了任务间隔参数λb及随机竞争失效事件对维修决策的影响，从侧面验证了模型的合理性和有效性。

由于模糊随机竞争失效及相关参数的α水平截集都有可能影响最终的维修方案，所以，在选择性维修决策建模时，不仅要考虑任务持续期间装备系统承受的随机RCF事件，还要综合权衡模糊参数α水平截集的影响，这样才能为决策者制定维修方案提供准确可信的理论依据和参考。