（0.5-100）mm量块中心长度测量结果的扩展不确定度评定

齐皇仲 陆韬

浙江省方正校准有限公司 浙江杭州 310013

量块作为一种实物量具，能够提供一个非常稳定的端度类测量标准，我们制造类企业在实际生产中经常需要用到量块或者用于比对测量产品，或者用于校对量具，应用可谓广泛。因此对量块的校准就有广泛的需求，而校准量块就必须评定其测量不确定度[1]。

1 概述

测量依据：JJG146-2011《量块检定规程》。

测量条件：温度（20±0.6），相对湿度≤65%。

计量标准：（0.5-100）mm3等量块。

被测对象：（0.5-100）mm4等量块。

测量方法：为使标准量块和被测量块的温度达到近似相等，测量前两量块需同时放置在工作台上等温。测量时，先将标准量块放入量块比较仪下，比较仪置零，再移至被测量块，得到与标准量块中心长度差值δ。δ与标准量块中心长度的实际值Ls之和即为被测量块中心长度的实测结果L。

2 测量模型

L=δ+Ls

式中：L-被测量块中心长度，单位：mm；

δ-被测量块与标准量块中心长度差值，单位：mm；

Ls-标准量块中心长度，单位：mm。

3 不确定度传播率

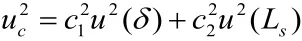
式中δ的灵敏系数c1=∂L/∂δ=1

Ls的灵敏系数c2=∂L/∂Ls=1

4 输入量的标准不确定度评定

4.1 输入量δ标准不确定度u（δ）的评定

输入量δ的标准不确定度来源由3个不确定度分量构成；

a测量重复性引起的标准不确定度u(δ1)；

b标准和被测量块的线膨胀系数之差Δα引起的标准不确定度u(δ2)；

c标准量块与被测量块温度差Δt引起的标准不确定度u(δ3)；

（1）u（δ1）的评定。测量重复性引入的标准不确定度采用A类方法评定，选取100mm量块1块，用量块比较仪在重复性条件下连续比较测量10次，得到测量列0.62，0.69，0.73，0.58，0.55，0.64，0.59，0.62，0.65，0.63,单位：μm。按贝塞尔公式计算，得到单次实验标准差S＝u(δ1)：

同理可得10mm量块的测量重复性引入的标准不确定度26nm、50mm量块的测量重复性引入的标准不确定度33nm。

自由度均为：

ν(δ1)=10－1=9

（2）u（δ2）的评定。从规程得知，量块所用钢材料的线膨胀系数应为（11.5±1）×10-6℃-1，被测量块温度tx与标准温度20℃的偏差不超过0.6℃。假定标准和被测量块的线膨胀系数在（11.5±1）×10-6℃-1范围内均匀分布，半宽区间α为1×10-6℃-1，标准不确定度u(δ2)为

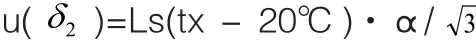
则对于100mm量块：

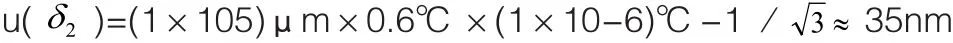
同理可得10mm量块的u δ2)=4nm、50mm量块的u（δ2）=18nm。

估计其相对标准不确定度为10%，则自由度为：

ν(δ2)=1／(2×0.12)=50

（3）u(δ3)的评定。原则上要求标准量块与被测量块温度达到等温后进行测量。但实际测量时，两量块通常有一定的温差Δt，估计温差在±0.1℃范围内，且均匀分布，则该分布半宽α为0.1℃，故由Δt引起的标准不确定度u(δ3)为：

对于100mm量块：

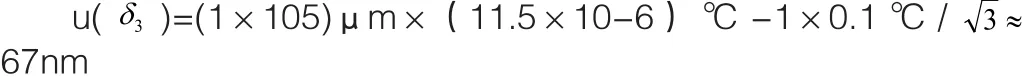
同理可得10mm量块的u(δ3)=7nm、50mm量块的u（δ3）=33nm。

估计u(δ3)的相对标准不确定度为10%，则其自由度：

ν(δ3)=1／(2×0.12)=50

（4）合成标准不确定度uc(δ)的计算。对于100mm量块：

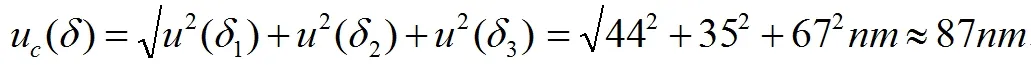
同理可得10mm量块的uc(δ)=27nm、50mm量块的uc(δ)=50nm。

合成自由度公式为：

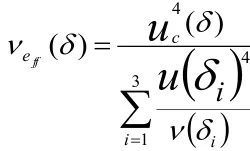
则得 到10mm量块的νeff(δ)=10、50mm量 块的νeff(δ)=39、100mm量块的νeff(δ)=100。

4.2 输入量Ls标准不确定度u(LS)的评定

标准量块中心长度Ls的标准不确定度u(Ls)及其自由度取自3等量块溯源证书中扩展不确定度评定结果[2-3]。结果如下：

10mm量块的u(LS)=32nm、50mm量块的u(LS)=49nm、100mm量块的u(LS)=57nm。

10mm量块的ν(Ls)=100、50mm量块的ν(Ls)=100、100mm量块的ν(Ls)=100。

5 合成标准不确定度uc的评定，见表1

合成标准不确定度公式：

合成自由度公式：

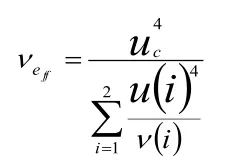
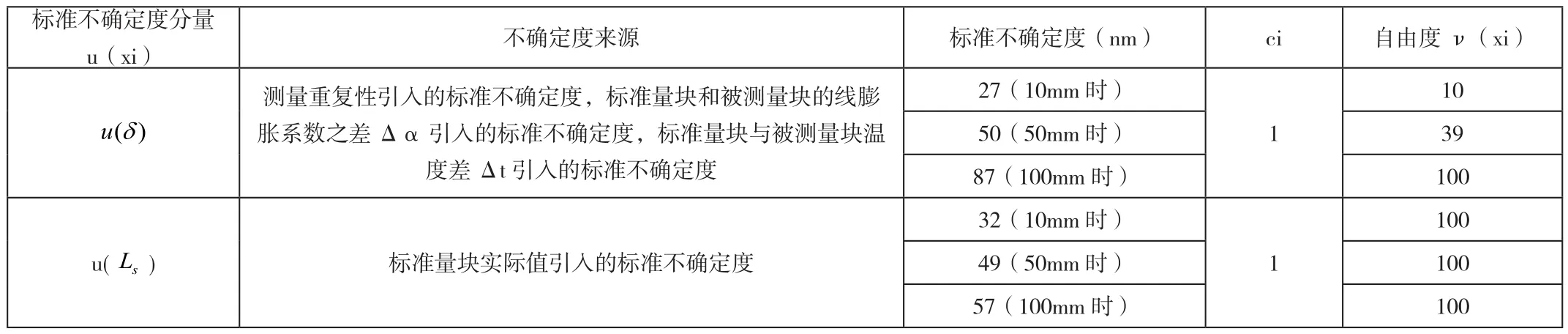
表1 输入量的标准不确定度汇总一览表

uc与νeff计算结果如下：

10mm量块的uc=42nm、50mm量块的uc=70nm、100mm量块的uc=104nm。

10mm量块的νeff=25、50mm量块的=100、100mm量块的=100。

6 扩展不确定度Up的计算

Up=kp·uc=tp(νeff)·uc

取置信概率P=0.99，查表可得kp值。

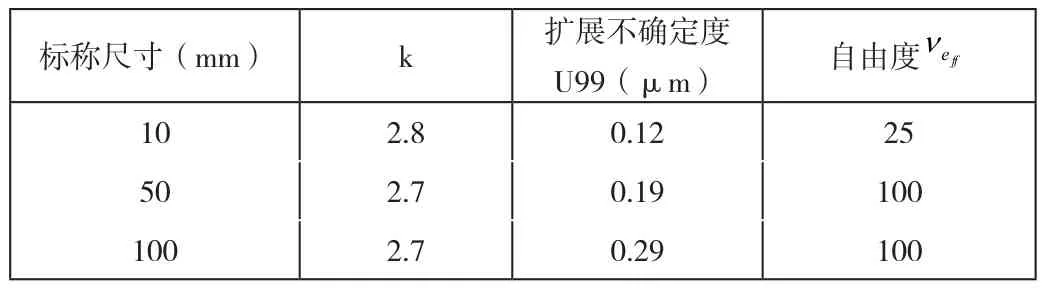
表2 各尺寸Up一览表

7 校准和测量能力（CMC）

4等量块校准和测量能力（CMC）为：

（0.5-100）mm：U=0.08μm+1.4×10-6×ln，k=2。（ln为校准点量块的标称长度，单位：μm）

8 结语

希望本文能为大家在评定量块中心长度测量结果的扩展不确定度的工作中提供一些参考。