微小型MEMS测试标定实验仪伺服系统设计

张 鹏，李维刚，王树森，李孟委,2，李 登

(1.中北大学 电子测试技术国家重点实验室，山西 太原 030051；2.中北大学 仪器与电子学院，山西 太原 030051)

微机电系统(Micro-Electro-Mechanical Systems，MEMS)是基于半导体制造技术在微电技术基础上发展而来的，一般使用光刻、腐蚀等工艺，是对微米纳米材料进行设计、加工、制造、测量和控制的技术.MEMS技术集微型机构、传感、控制等多个功能于一体，是一种具有信息获取、处理等多种功能的系统[1].该系统凭借体积小、重量轻、功耗低、价格低、性能稳定等优点，在军用和民用领域均得到广泛的应用[2].

稳定平台是一种具有防抖隔震、稳瞄稳像、目标跟踪等功能的标定测试仪器，被广泛应用于坦克炮塔稳瞄、舰船炮塔稳瞄、无人机光电吊舱、空空导弹导引头、民用航拍摄影防抖等领域[3-5].目前世界范围内的高精度三维伺服平台发展很快，美、英等国在役的武器装备上相当广泛地使用了基于微惯性的传感器跟踪平台.我国于上世纪八十年代研制出了稳瞄式的平台，而研制陀螺式的稳定平台工作也在九十年代初得到了全面的开展.北京618所研制的机载陀螺式稳定平台，其精度已经达到了0.1 mrad.

传统的高精度惯性测试稳定平台主要针对高精度的光学惯组、机械陀螺等，体积大、成本高，应用于MEMS惯性器件必将造成测试资源的浪费[6-8].本文设计了一款面向实验教学的稳定平台，其兼具对中低精度MEMS器件进行测试标定的功能，在控制成本及仪器整机体积的前提下设计伺服控制系统，提高了控制精度.

1 系统设计

1.1 技术指标

为使所设计的测试标定系统能够对采用串行外设接口(Serial Peripheral Interface，SPI)和串口输出数字信号的MEMS传感器进行测试标定，系统可进行MEMS加表、陀螺性能参数的测试标定以及微型惯性测量单元(Miniature Inertial Measurement Unit，MIMU)的安装误差标定.通过MIMU的标定实验可得到MEMS加表和MEMS陀螺的标度因数、零偏以及MIMU的安装误差，既可以实现器件的标定，也可用于性能筛选领域.平台系统设计的技术指标如表 1 所示.

表 1 技术指标

1.2 控制系统设计

伺服稳定平台的核心部分包括角速率测量、姿态测量部分，伺服回路控制部分和机械框架部分.

平台的构成及各个环节之间的关系如图 1 所示，从图中可以看出平台的核心部分为控制系统[9]，控制系统下达指令给驱动系统，驱动系统带动机械框架部分运动，框架运动后，传感器将测得值反馈给控制系统.这3个部分缺一不可，且需要按照一定的要求系统工作.作为平台核心的控制系统又由主控制器、配套主控制器的信号输入输出接口、通讯接口等组成；驱动系统主要由电机及驱动器组成；机械框架部分主要由用于平台和载体固连及平台与驱动电机连接的机械构件组成.

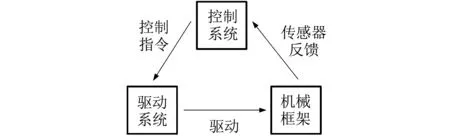
图 1 平台结构组成Fig.1 Platform structure composition

稳定平台的主控制芯片如图 2 所示，内置RS422及RS485通信电路，与上位机通过RS485通信，方便转台的位置控制与速率控制，与横滚轴和俯仰轴的RX28舵机采用RS422通信.

图 2 主控电路图Fig.2 Main control circuit diagram

图 3 为三轴陀螺稳定平台示意图.伺服稳定平台的原理[10]如图 4 所示，由陀螺仪提供角速率信息，反馈给速度控制器，矫正稳定平台干扰信号.同时陀螺仪输出角速率进行一次积分得到角度信息，反馈给位置控制器，形成位置-速度双闭环控制系统.

图 3 三轴陀螺平台示意图Fig.3 Schematic diagram of three-axis gyro platform

图 4 陀螺稳定平台原理Fig.4 Principle of Gyro Stabilized platform

2 非水平干扰信号

稳定平台功能中的非水平干扰信号能否准确获取是实现该功能演示的关键.常见的抖动干扰信号源产生于六自由度摇摆平台，但该方法需要重新设计一套六自由度摇摆平台系统，大大增加了系统的复杂度和仪器成本.因此，将仪器基座倾斜角度θ，认为产生一个俯仰角，然后通过Z轴旋转实现非水平干扰信号，方法简单，几乎不用增加硬件设备.

传统的稳定平台测试方法包括静态跟踪测试和动态摇摆测试，静态测试主要是将稳定平台放置于高精度转台上，通过高精度转台设定一个倾角位置，让稳定平台跟随到该已知位置，利用稳定平台自带的高精度码盘测量位置跟踪精度；动态测试是指将稳定平台放置于高精度摇摆台上，摇摆台按照一个正弦变化的角度信号做周期运动，通过调节摇摆台的摇摆周期测量稳定平台跟随的动态特性.

图 5 为陀螺稳定平台的系统框图，包括稳定平台和非水平干扰信号源.稳定平台实物图如图 6 所示.

图 7 为稳定平台功能干扰信号源产生机理.其中MEMS惯组提供俯仰轴和横滚轴姿态，传输给稳定平台俯仰轴电机和横滚轴电机，以调整转台内框水平.转台航向轴由上位机软件控制，使转台外框在倾斜状态下做摇摆运动，为中框和内框提供非水平干扰信号.

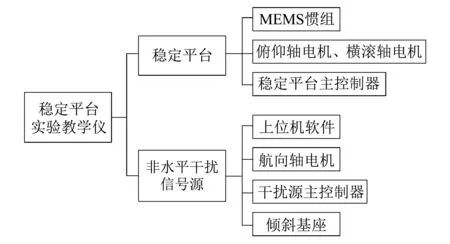
图 5 陀螺稳定平台系统框图Fig.5 Diagram of Gyro stabilized platform system

图 6 稳定平台实物图Fig.6 Picture of Gyro stabilized platform

图 7 稳定平台功能干扰信号源产生机理Fig.7 Generation mechanism of stabilizing platform function jamming signal source

稳定平台的教学演示及测量方法用于测试稳定平台的教学实验中，包括以下测量步骤：

1) 给稳定平台提供一非水平干扰信号源，计算获得稳定平台的俯仰角α1、横滚角β1；

2) 稳定平台调节自身姿态，保持平台处于稳定平衡状态，并通过电机码盘获得测量稳定平台的俯仰角α2、横滚角β2；

3) 计算比较α1与α2的误差，β1与β2的误差，获得稳定平台的整体误差水平，完成教学试验.

如果要求一种面向实验教学的稳定平台测试方法，所述步骤1)的非水平干扰信号源包括一个倾斜基座、一个航向轴电机及一个内框平台.内框平台的水平姿态角α和β通过下式产生干扰信号

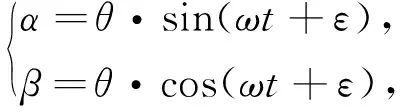
式中：α为所述内框平台的俯仰角；β为所述内框平台的横滚角；θ为所述倾斜基座的倾斜角度；ω为所述航向轴电机的转动角速率；ε为所述航向轴电机转动的初始相位角.

扰动基座装置包括倾斜基座、航向电机控制单元、航向轴电机及内框平台.抖动干扰信号源引起的俯仰角和横滚角与Z轴转动角速率成正余弦变化.陀螺稳定平台控制所需姿态角由陀螺仪测量得到.由上式可知，当ω为常数时，俯仰角和横滚角呈正余弦变化，相位相差90°；当ω以一次函数变化时，俯仰角和横滚角按照频率随时间呈正余弦变化；当ω以正弦函数变化时，俯仰角和横滚角变化规律复杂，相位相差90°；当ω以白噪声信号变化时，俯仰角和横滚角开始无规律变化，将形成严重的干扰信号.图 8 为角速率ω按照一次函数变化时，平台内框俯仰角和横滚角的姿态变化曲线图.

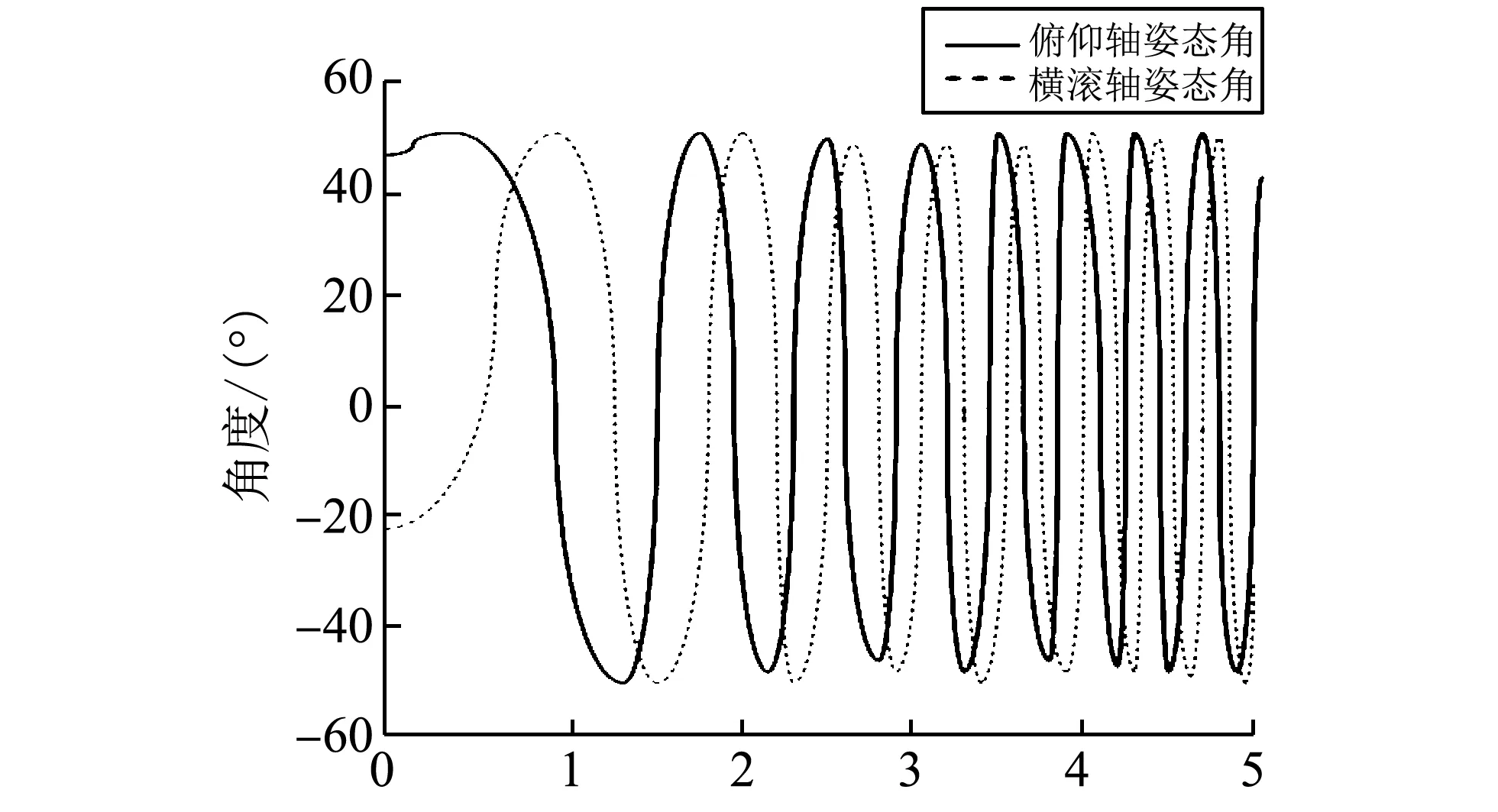
图 8 角速率按一次函数变化时的姿态角Fig.8 The attitude angle of angular rate changing at one time function

图 9 为角速率按照正弦函数变化时，平台内框俯仰角和横滚角的姿态变化曲线图.通过调整不同的ω和θ角度，可以实现任意的非水平干扰信号.

图 9 角速率按正弦变化时的姿态角Fig.9 Attitude angle of angular rate in the case of sinusoidal variation

3 控制策略及Simulink仿真

设计的双轴陀螺稳定平台可以看作是两个单轴陀螺稳定平台系统的组合.单轴陀螺稳定系统的工作原理、系统特性、分析方法、评估指标等都适用于双轴陀螺稳定平台.依据稳定平台的工作原理，将各个部分简化成传递函数的形式，得到如图 10 所示的平台稳定原理框图.其中，速度环反馈由陀螺仪输出的角速率提供，位置环由惯性测量单元(Inertial Measurement Unit，IMU)提供.

根据稳定平台控制系统原理建立Simulink仿真，仿真包括速率陀螺的速度环反馈回路和位置跟踪环反馈回路.电机的参数根据直流电机的实际指标进行配置.输入幅值为10°的阶跃位置信号，载体干扰角速度设为幅值为0.2、频率为2 Hz的正弦信号ωb(t)=sin(4πt) rad/s，力矩输入为2.通过调节速度环PID(Proportion Integral Derivative)和位置环PID使得系统达到速率精度0.1 °/s 和位置精度0.01°.

图 10 平台稳定原理框图Fig.10 Principle diagram of platform stability

通过仿真得到图 11 的阶跃响应曲线和图 12 的正弦位置变化跟踪曲线.仿真结果表明所设计的陀螺稳定平台伺服系统的控制策略能满足陀螺稳定平台控制需求.

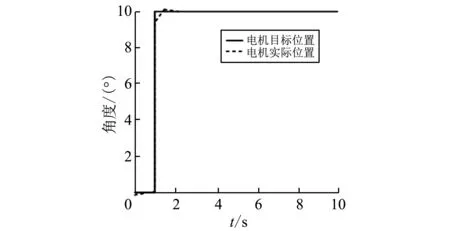
图 11 平台稳定位置控制系统仿真图Fig.11 Simulation diagram of platform stabilized position control system

图 12 平台稳定位置跟踪仿真图Fig.12 Platform stable position tracking simulation diagram

4 结 论

从学生教学稳定平台试验仪出发，结合目前MEMS加速度计、MEMS陀螺以及MIMU信号输出形式，提出了系统设计的主要技术指标；结合三轴陀螺稳定平台，对平台控制系统进行了设计，分析了干扰信号的耦合机理，并解释了稳定平台隔离震动的工作原理；最后，通过建模和Simulink仿真得到陀螺稳定平台常用的双闭环控制原理.仿真结果表明所设计的陀螺稳定平台伺服系统的控制策略能满足陀螺稳定平台控制需求.