弹丸头部形状对弹道偏流现象的影响

刘铁磊，梁化鹏，沈培辉

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.西安现代控制技术研究所，陕西 西安 710065)

0 引 言

在进行实弹射击时，常常会发现靶位上的枪弹落点中心偏离射击面，这种现象称为偏流[1].传统上，偏流产生的原因归结于动力平衡角[2]，且右旋弹丸产生右偏流，左旋弹丸产生左偏流[3].近年来，随着计算流体动力学(Computational Fluid Dynamics，CFD)软件的流行，更多的学者从空气动力学角度对偏流现象进行解释.何颖等[1]对不同转速和不同攻角条件下，弹丸的受力分布进行数值模拟，证明了弹丸在低速飞行过程中，会产生偏向旋转方向的偏流.雷娟棉等[4]从流场结构和气动特性两个方面，对偏流现象的成因——马格努斯效应进行了讨论，证明了边界层的非对称畸变是马格努斯效应产生的重要原因，并得出船尾对马格努斯效应有重要影响.肖中云等[5]在此基础上就船尾形状对马格努斯效应的影响进行了研究.

尽管目前对弹道偏流的研究已有不少，然而对弹丸不同部位对偏流的贡献程度的研究仍然缺乏，尤其是缺乏关于弹丸头部形状对弹道偏流现象的研究.

1 理论分析

由于偏流实际上是在靶位上，中心弹着点关于竖直射击面z轴方向的偏移.因此，可以从六自由度外弹道方程出发，分析产生偏流现象的直接原因.无风条件下，六自由度外弹道方程为[6]

(1)

若仅考虑质心运动，式(1)可退化为

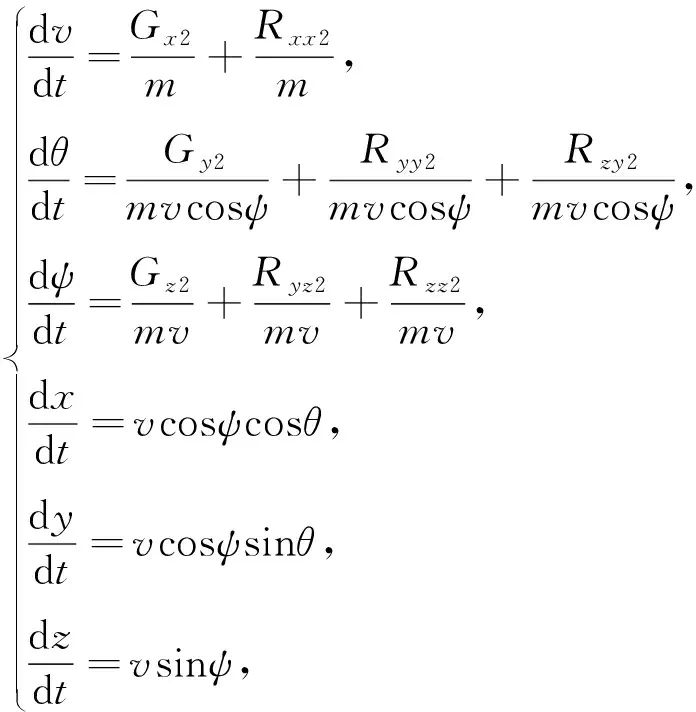
(2)

式中：v为弹丸速度；θ为弹道倾角；ψ为弹道偏角；x,y,z分别为弹丸实时位置坐标；G为弹丸重力；Rx为弹丸阻力；Ry为弹丸升力；Rz为弹丸马格努斯力；下标表示各力随弹轴坐标系投影的分量.

式(2)中，z即反映弹丸的偏流，z的大小可清楚反映弹丸偏移量的大小.对式(2)进一步化简，以弹丸运动的x坐标为自变量，消去变量t，则

式(3)表示，当弹丸射程一定时，弹道偏流和弹丸重力、升力、马格努斯力和弹丸速度有关.

弹丸升力和马格努斯力的表达形式如下

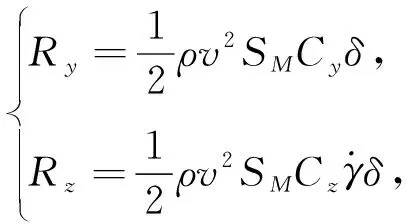
(4)

式中：Cy,Cz分别为弹丸升力系数和马格努斯力系数，反映了弹丸的形状特征.而弹丸速度也与弹丸阻力有关，弹丸阻力的表达形式为

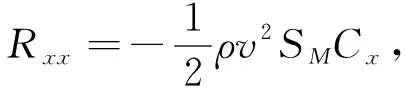
(5)

其阻力系数同样受弹丸形状的影响.

蓝志环等[7]推导的偏流公式同样反映了影响偏流的几个因素

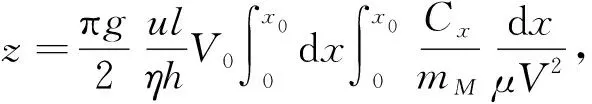
(6)

式中：Cx为空气动力学系数，同样反映了弹丸形状的影响.在弹丸形状中，弹头形状可对弹丸飞行产生重要影响.封贝贝等[8]对不同头部形状的飞行器在超声速条件下进行了风洞试验，发现头部形状显著影响激波阻力的大小，头部长宽比是影响激波阻力的关键因素.刘宣等[9]对引信形状对射程的影响进行了研究，发现抛物线外形和准球头外形均能增加平头弹的射程.然而这些研究均着眼于弹丸头部形状对飞行阻力和射程的影响，对偏流与弹头形状的关系研究较少.因此，下文通过将流场分析和六自由度外弹道方程联立，对弹头形状和偏流现象之间的关系进行研究.

2 仿真计算

2.1 仿真模型

基于低侵彻终点效应的要求，设计了一种凹头低侵彻弹药[10].该弹与尖头弹长度、质量、截面积和转动惯量均保持一致，而头部形状不同，适合作为研究蓝本.在此基础上，提出加风帽的改进方案，在保证低侵彻终点效应的要求同时，优化弹头部形状.

3种弹药的外形图如图 1 所示.

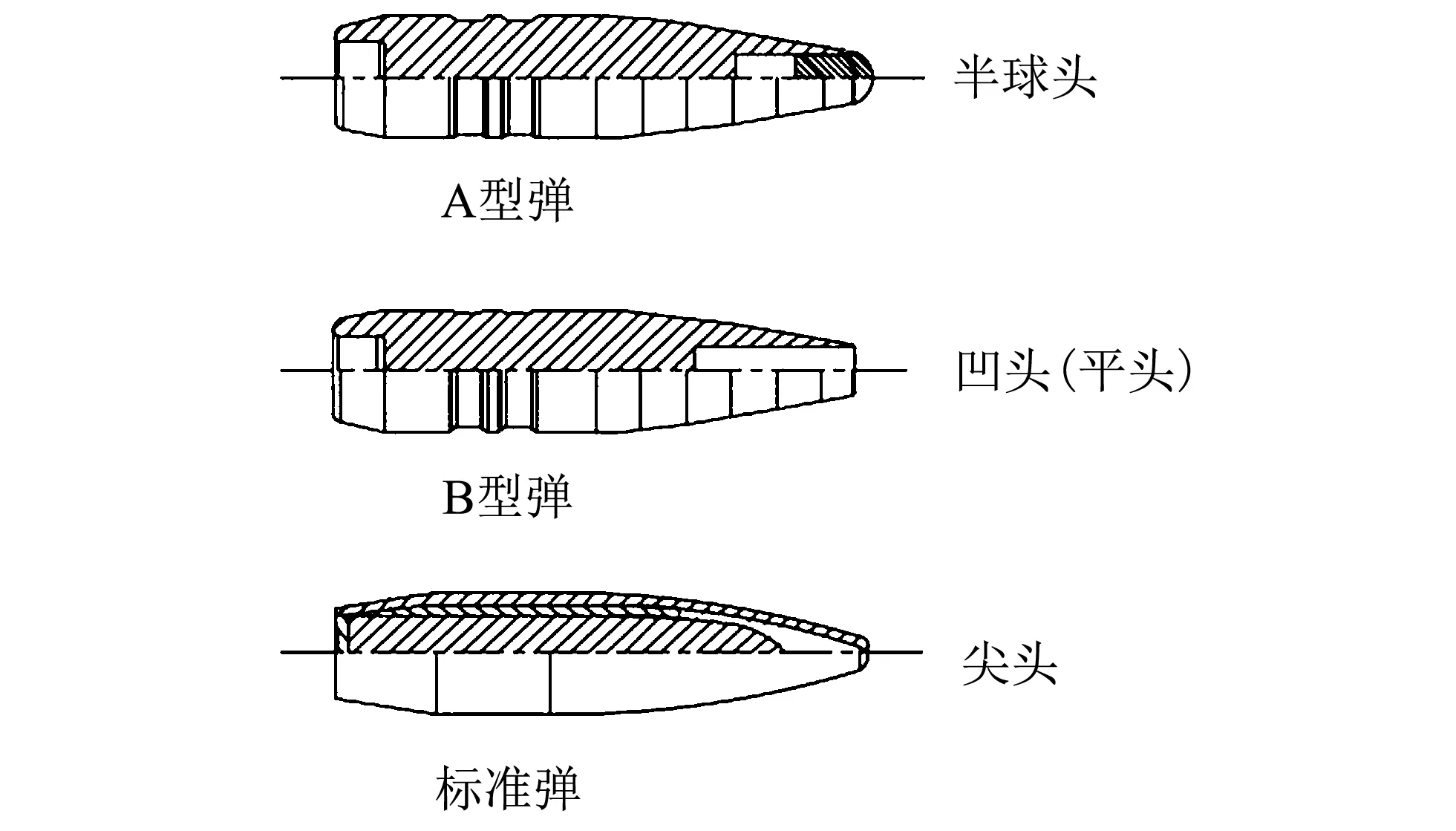
图 1 仿真弹体外形结构图Fig.1 Simulated projectile configuration

为不影响终点效应，风帽采用橡胶/塑料等轻质易变形材料.3种弹药的部分结构参数如表 1 所示.

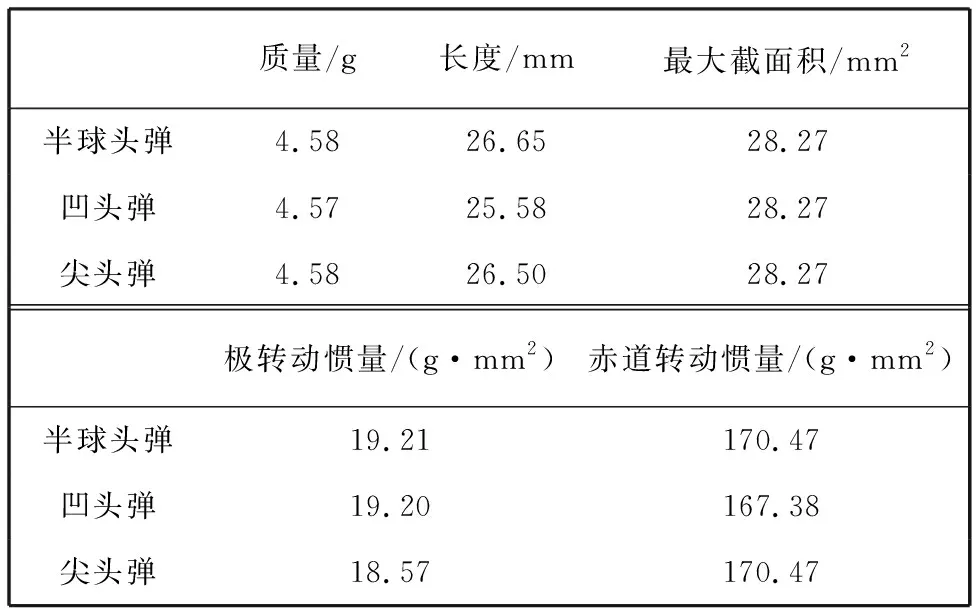
表 1 3种弹型部分结构尺寸参数

2.2 仿真方法

3种弹型的仿真设置方法类似.仿真借鉴文献[11]的方法，在gambit中，将模型的空气域离散化.3种弹型的网格拓扑图如图 2 所示.

采用双层空气域以便赋予弹体转速，内外域以交界面形式联系.设置弹体为壁面，外空气域表面为压力远场边界条件.

欧拉方程与N-S方程均可以用于弹丸外流场的计算.由于N-S方程对于弹丸的阻力系数具有良好的计算性[12]，因此，选择Navier-stocks方程和Spalart-Allmaras湍流模型简化计算，加快收敛.

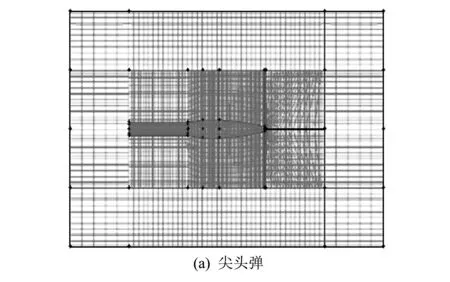
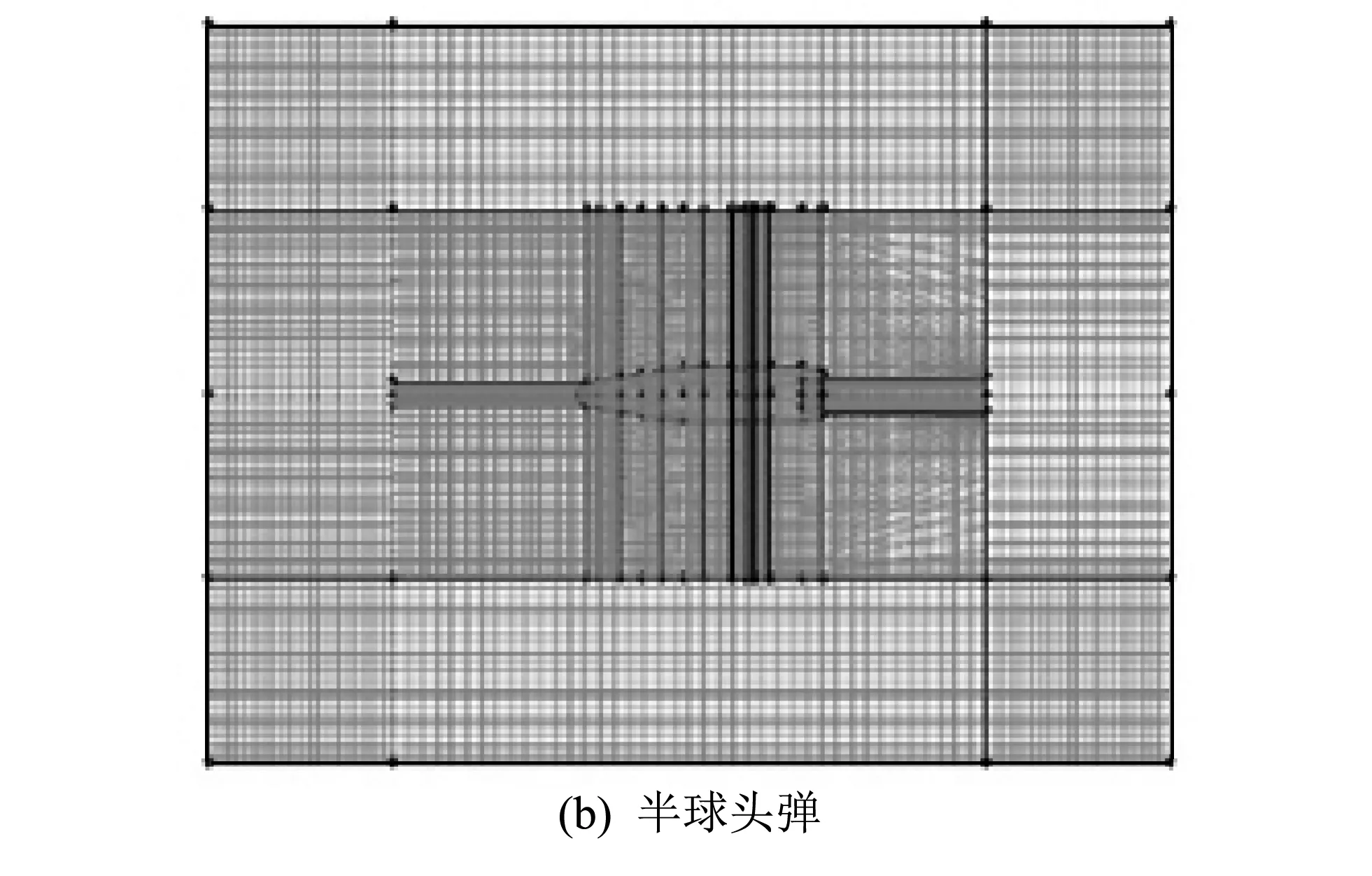
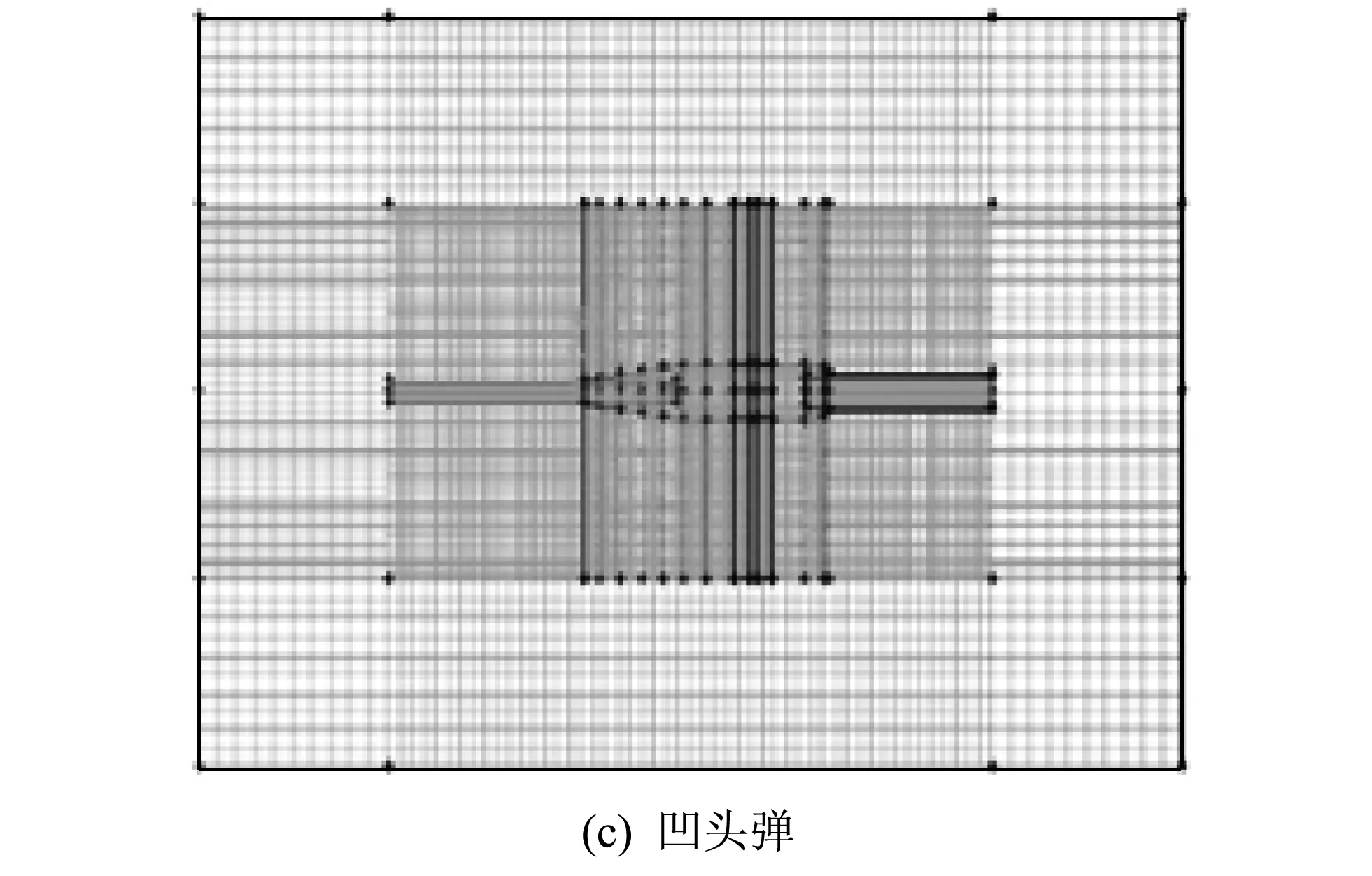
图 2 网格拓扑图Fig.2 Grid topology

对于牛顿流体而言，决定流体运动的方程如下所示

连续方程

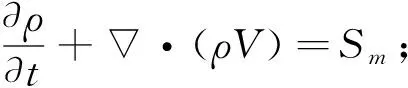
(7)

N-S方程

(8)

式中：

(9)

能量方程

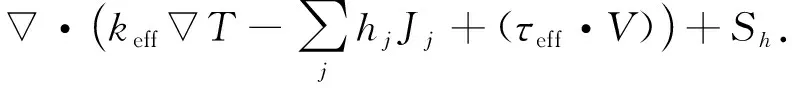
(10)

由于Spalart-Allnara模型具有计算量小的优点，对于结构简单的模型，选择单方程Spalart-Allnara为湍流粘性模型具有良好的收敛性.采用密度基求解器和Green-Guass Node Based求梯度的方法可以确保求解精度.

2.3 仿真结果

对3种弹型在马赫数为2.676，弹丸转速为800 rad/s，迭代步长为3 000的初始条件下进行仿真，仿真结果如图 3 所示.图中弹头前方的浅色色块表明此处动压较低，证明此处存在压力停滞区.由图可以看出尖头弹的压力停滞区较小，凹头弹的压力停滞区较大.压力停滞区越大，表明弹头所受的空气阻力越大，因此从直观上来说，凹头弹的空气阻力最大.此外由图3(d)凹头弹的动压剖面图可知，凹头部分的动压为0，内部空气在弹丸飞行过程中受弹前压力的作用而停滞，不对飞行产生任何效果，故在空气动力学仿真上，凹头可近似作为平头处理.

图 3 三种弹丸动压云图Fig.3 Dynamic pressure nephogram of three bullet

对3种弹丸攻角在0°～5°变化时的阻力系数进行计算，计算结果如表 2 所示.

比较在各攻角下的3种弹型的空气阻力系数，可以发现在各攻角下，尖头弹的阻力系数最小，凹头弹的阻力系数最大，验证了之前的直观印象.同时，在小攻角条件下，同种弹丸的阻力系数差异不大，因此在进行外弹道计算时，可以零升阻力系数替代.

根据第1节的理论分析，可以认为尖头弹的偏流程度应低于半球头弹和凹头弹.由于式(2)和式(3)涉及的多个气动参数难以准确确定，不宜直接通过理论进行计算.因此利用试验手段，对理论进行定性验证.

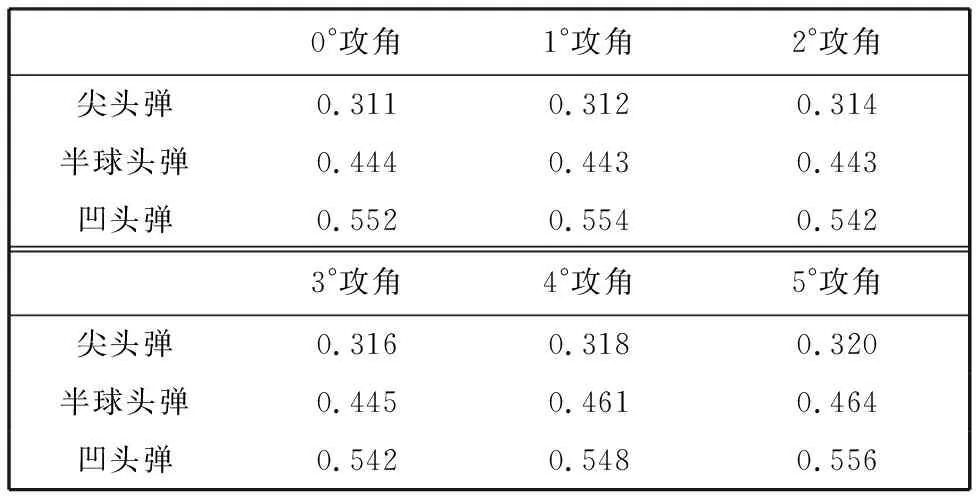
表 2 3种弹型在攻角0°～5°变化时的阻力系数

3 试验验证

在外场对3种弹型的外弹道特性进行测试，一共进行了3组实验，每组10发，在距离枪口5 m 处布置测速靶，记录弹丸初速；在距离枪口150 mm处布置后效靶，观察3种弹型的散布情况，其中3种弹型的实物如图 4 所示.

图 4 实弹图 Fig.4 Bullet diagram

图 4 中，凹头弹和半球头弹的差别仅仅在其头部形状不同，由于风帽质量远小于弹丸质量，故两者质量和转动惯量之间的差异可忽略不计.试验结果如图 5 所示.

图 5(a) 为尖头弹与凹尖头进行对比试验的试验结果，图 5(b) 为尖头弹与半球头弹进行对比试验的试验结果，图 5(c) 为尖头弹与半球头弹进行对比试验的试验结果.从图上可以看出，半球头弹与凹头弹的中心落点均较尖头弹中心落点右偏，证明两弹的弹道特性均不如尖头弹；在半球头弹与凹头弹的对比试验中，发现凹头弹的中心落点较半球头弹右偏，以上规律符合之前的理论仿真分析.3种弹型的相对偏流程度如表 3 所示.

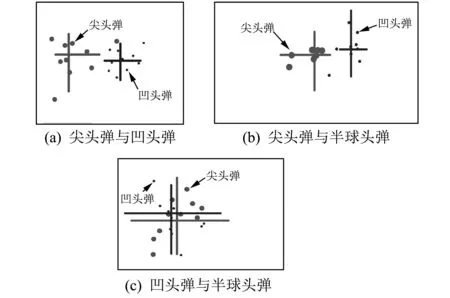
图 5 试验射弹分布图Fig.5 Test bullet distribution

尖头弹与凹头弹尖头弹与半球头弹半球头弹与凹头弹横向偏流差/cm12.98.61.2

表 3 的结果总体上反映了弹丸阻力越大，偏流程度越大的规律，证明了弹丸头部形状对弹道偏流现象存在影响.当然，由于试验弹丸的数量较少，射击连续等原因，试验数据存在一定的误差.例如若按前两组试验的试验结果推测，凹头弹应较半球头弹右偏4.3 cm，而在第3组试验中，凹头弹仅较半球头弹右偏1.2 cm.但综合以上结论，均有如下规律：弹丸质量和弹身形状一定时，弹丸头部形状越尖锐，弹道偏流程度越小.

4 结 论

本文从六维外弹道方程入手，对弹丸的偏流现象进行分析，发现弹丸阻力系数与弹道偏流存在某种关系.基于弹丸头部形状极大影响弹丸飞行阻力的共识，先后建立了3种头部形状不同的弹丸的模型，对其在不同攻角条件下的空气阻力系数进行计算，计算结果表明，弹丸头部形状越尖锐，弹丸的阻力系数越小.随后的弹道试验结果也证明了弹丸头部形状越尖锐，弹道偏流越小.本文结论可为今后的弹丸设计提供参考.