椭圆型交换四元数矩阵的实表示及逆矩阵求法

孔祥强

(菏泽学院 数学与统计学院，山东 菏泽 274015)

0 引 言

四元数量子力学是现代量子力学的重要分支，它是建立在非交换四元数代数上的量子力学，与一般的复量子力学不同.四元数代数和分裂四元数代数是两个结合且非交换的四维克利福德代数，与四元数代数不同，分裂四元数代数不是除环，且含有零因子、幂零元和幂等元[1-4].目前，关于分裂四元数的研究成果非常丰富[5-8].文献[9]中，Segre首次研究了满足乘法交换律的交换四元数代数理论，开创了交换四元数理论研究的新领域，使交换四元数代数的应用更加广泛[10-13].文献[14-15]研究了交换四元数的分类，具体有椭圆型、抛物型、双曲型及特殊型等.文献[16]研究了椭圆型交换四元数，得到了复表示下的系列成果.本文研究椭圆型交换四元数的实表示，得到椭圆型交换四元数矩阵实表示的系列性质，进而研究了椭圆型交换四元数矩阵的特征值，并给出求椭圆型交换四元数矩阵逆矩阵的方法.

1 椭圆型交换四元数的实表示

设H={a=a0+ia1+ja2+ka3}，a0,a1,a2,a3∈R，R为实数域，且满足i2=-1，j2=1，k2=-1，ij=ji=k，jk=kj=i，ki=ik=-j，ijk=-1，称满足条件的交换四元数a为椭圆型交换四元数[14].

定理 1 任意一个椭圆型交换四元数均与实数域上的4阶矩阵同构.

证明 设a=a0+ia1+ja2+ka3∈H，a0,a1,a2,a3∈R，定义映射φa∶H→H，φa(b)=ba，∀b∈H，则映射为双射且

φa(1)=1a=a0+ia1+ja2+ka3,

φa(i)=ia=-a1+ia0-ja3+ka2,

φa(j)=ja=a2+ia3+ja0+ka1,

φa(k)=ka=-a3+ia2-ja1+ka0.

记

R4×4=

则H和R4×4本质是相同的.实数域上4阶矩阵的性质即为椭圆型交换四元数的性质，故对椭圆型交换四元数的研究可转化为对实数域上4阶矩阵的研究.

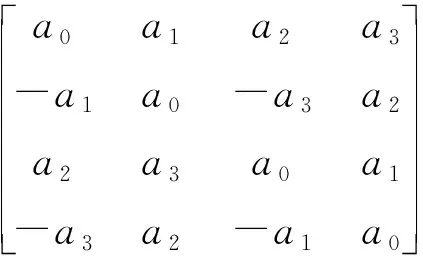
a的共轭形式主要有3种：a(1)=a0-ia1-ja2+ka3,a(2)=a0+ia1-ja2-ka3,a(3)=a0-ia1+ja2-ka3, 则

2 椭圆型交换四元数矩阵的实表示及性质

记

R4n×4n=

则Hn×n和R4n×4n本质是相同的.实数域上4n阶矩阵的性质即为椭圆型交换四元数矩阵的性质，故对椭圆型交换四元数矩阵的研究可转化为对实数域上4n阶矩阵的研究.

设A∈Hn×n，AR为A的实表示矩阵，定义A的q-行列式为|A|q=|AR|[16].

设A,B∈Hn×n，若AB=BA=In，In为n阶单位矩阵，则称矩阵A可逆，且B为A的逆矩阵[16].

性质 1 设A,B∈Hn×n，且满足AB=In，则BA=In.

证明

A=A0+iA1+jA2+kA3，

B=B0+iB1+jB2+kB3，

A0,A1,A2,A3∈Rn×n，

B0,B1,B2,B3∈Rn×n，

AB=In，

AB=(A0B0-A1B1+A2B2-A3B3)+

i(A0B1+A1B0+A1B0+A2B3+A3B2)+

j(A0B2-A1B3+A2B0-A3B1)+

k(A0B3+A1B2+A2B1+A3B0),

则

A0B0-A1B1+A2B2-A3B3=In,

A0B1+A1B0+A2B3+A3B2=0,

A0B2-A1B3+A2B0-A3B1=0,

A0B3+A1B2+A2B1+A3B0=0,

即

所以

则

B0A0-B1A1+B2A2-B3A3=In,

B1A0+B0A1+B2A3+B3A2=0,

B0A2-B1A3+B2A0-B3A1=0,

B0A3+B1A2+B2A1+B3A0=0,

又

BA=(B0A0-B1A1+B2A2-B3A3)+

i(B0A1+B1A0+B2A3+B3A2)+

j(B0A2-B1A3+B2A0-B3A1)+

k(B0A3+B1A2+B2A1+B3A0),

故BA=In.

注 1 设A,B∈Hn×n，且满足BA=In，则AB=In.

性质 2 设A,B∈Hn×n，则

1) (A+B)R=AR+BR；

2)ARBR=(AB)R；

3) 设α∈R，则(αA)R=αAR；

4) 若A可逆，则(A-1)R=(AR)-1；

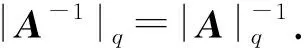
证明

1)A+B=(A0+B0)+i(A1+B1)+j(A2+B2)+k(A3+B3)，则

(A+B)R=

AR+BR.

2) 令

ARBR=

则

p11=A0B0-A1B1+A2B2-A3B3,

p12=A0B1+A1B0+A2B3+A3B2,

p13=A0B2-A1B3+A2B0-A3B1,

p14=A0B3+A1B2+A2B1+A3B0,

p21=-A1B0-A0B1-A3B2-A2B3,

p22=-A1B1+A0B0-A3B3+A2B2,

p23=-A1B2-A0B3-A3B0-A2B1,

p24=-A1B3+A0B2-A3B1+A2B0,

p31=A2B0-A3B1+A0B2-A1B3,

p32=A2B1+A3B0+A0B3+A1B2,

p33=A2B2-A3B3+A0B0-A1B1,

p34=A2B3+A3B2+A0B1+A1B0,

p41=-A3B0-A2B1-A1B2-A0B3,

p42=-A3B1+A2B0-A1B3+A0B2,

p43=-A3B2-A2B3-A1B0-A0B1,

p44=-A3B3+A2B2-A1B1+A0B0.

又

AB=(A0+iA1+jA2+kA3)·

(B0+iB1+jB2+kB3)=

(A0B0-A1B1+A2B2-A3B3)+

i(A0B1+A1B0+A2B3+A3B2)+

j(A0B2-A1B3+A2B0-A3B1)+

k(A0B3+A1B2+A2B1+A3B0),

u21=p21,u22=p22,u23=p23,u24=p24,

u31=p31,u32=p32,u33=p33,u34=p34,

u41=p41,u42=p42,u43=p43,u44=p44.

故ARBR=(AB)R.

3)

性质 3 设A=A0+iA1+jA2+kA3∈Hn×n，B=B0+iB1+jB2+kB3∈Hn×n，则

1) (AB)†1=B†1A†1，(AB)†2=B†2A†2，(AB)†3=B†3A†3；

2) (A(i))T=(AT)(i)，i=1,2,3；

3) (AB)(i)=A(i)B(i)，i=1,2,3；

4) (AB)T=BTAT；

5) 若A,B均可逆，则(AB)-1=B-1A-1；

6) 若A可逆，则(A-1)†1=(A†1)-1，(A-1)†2=(A†2)-1，(A-1)†3=(A†3)-1；

7) 当i≠j≠k时，(A(i))(j)=A(k)；当i=j时，(A(i))(j)=A，其中i,j,k∈{1,2,3}.

证明 2)～7)的结论易证得，这里仅给出1)的证明.

令

A=S1+jS2,B=T1+jT2,

其中

S1=A0+iA1,S2=A2+iA3,

T1=B0+iB1,T2=B2+iB3.

①

(AB)†1=[(S1T1)′+(S2T2)′-

B†1A†1=

故(AB)†1=B†1A†1.

②

(AB)†2=[S1T1+S2T2-j(S1T2+S2T1)]T=

故(AB)†2=B†2A†2.

③

(AB)†3=[(S1T1)′+(S2T2)′+j((S1T2)′+

故(AB)†3=B†3A†3.

3 椭圆型交换四元数矩阵的特征值

设A∈Hn×n，λ∈H，若Ax=λx，其中x为非零的交换四元数列向量，则称λ为A的特征值.A的特征值的集合称为A的谱集合，记作φ(A)={λ∈H∶Ax=λx,x≠0}[16].

定理 2 设A∈Hn×n，λ=λ0+iλ1+jλ2+kλ3∈H，则λ为A的特征值的充分必要条件是存在非零的n维实向量x0,x1,x2,x3，满足

证明A=A0+iA1+jA2+kA3，λ=λ0+iλ1+jλ2+kλ3∈H，λ0,λ1,λ2,λ3∈R，由Ax=λx，则

(A0+iA1+jA2+kA3)(x0+ix1+jx2+kx3)=

(λ0+iλ1+jλ2+kλ3)(x0+ix1+jx2+kx3),

即

(A0-λ0In)x0+(-A1+λ1In)x1+

(A2-λ2In)x2+(-A3+λ3In)x3=0,

(A1-λ1In)x0+(A0-λ0In)x1+

(A3-λ3In)x2+(A2-λ2In)x3=0,

(A2-λ2In)x0+(-A3+λ3In)x1+

(A0-λ0In)x2+(-A1+λ1In)x3=0,

(A3-λ3In)+(A2-λ2In)x1+

(A1-λ1In)x2+(A0-λ0In)x3=0,

所以

4 椭圆型交换四元数矩阵的逆矩阵

下面定理给出了求椭圆型交换四元数矩阵的逆矩阵的方法.

定理 3 设A∈Hn×n，且A的实表示矩阵AR可逆，则A可逆.

证明A=A0+iA1+jA2+kA3∈Hn×n，A0,A1,A2,A3∈Rn×n，则

不妨设

由AR(A-1)R=I4n，则

A0Q0-A1Q1+A2Q2-A3Q3=In,

A0Q1+A1Q0+A2Q3+A3Q2=0,

A0Q2-A1Q3+A2Q0-A3Q1=0,

A0Q3+A1Q2+A2Q1+A3Q0=0.

令Q=Q0+iQ1+jQ2+kQ3，其中Q0,Q1,Q2,Q3∈Rn×n，则

AQ=(A0Q0-A1Q1+A2Q2-A3Q3)+

i(A0Q1+A1Q0+A2Q3+A3Q2)+

j(A0Q2-A1Q3+A2Q0-A3Q1)+

k(A0Q3+A1Q2+A2Q1+A3Q0)=In.

由性质1知QA=In，故AQ=QA=In，A-1=Q0+iQ1+jQ2+kQ3.

注 2 设A∈Hn×n，由定理3知，以下命题等价

1)A可逆；2)方程Ax=0有唯一解；3)AR可逆；4)A没有零特征值.

注 3 定理3的证明过程即为求椭圆型交换四元数矩阵A的逆矩阵的过程.定理3提供的求A的逆矩阵的方法可通过计算机编程轻松实现.

5 数值算例

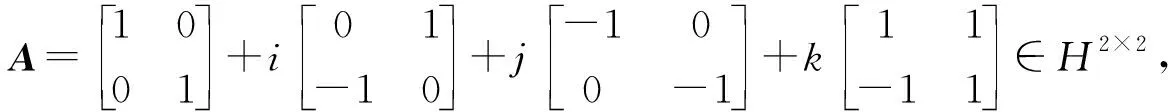
求得(AR)-1为

取

则

A-1=Q0+iQ1+jQ2+kQ3=

经检验，AA-1=A-1A=I2，故结论正确.

6 结 语

利用椭圆型交换四元数的实表示，研究了椭圆型交换四元数矩阵实表示的一系列性质，给出了此类矩阵特征值存在的充分必要条件，并得到了求此类矩阵的逆矩阵的方法，且通过算例说明了结论的正确性.在本文基础上，可进一步展开对椭圆型交换四元数矩阵其他问题的研究，如行列式问题、可对角化问题、矩阵的分解问题等.此外，也可进一步展开对其他类型的交换四元数及其矩阵的深入研究.