改进的边缘保护滤波分解融合算法

徐 甜，王军锋

(西安理工大学 理学院，陕西 西安 710054)

0 引 言

图像融合是组合通过不同传感器或同一传感器因成像目标不同获得的信息，使融合后图像包含更全面、丰富和准确的信息[1]。随着融合技术的发展，图像融合在计算机视觉、医学、军事和遥感以及人工智能等领域得到了广泛的应用，成为信息融合领域不可或缺的一部分。2000年，边缘保护分解滤波器成为了计算摄影和图像处理中的有效工具[2]，这些滤波器能够保护图像空间结构的一致性，并且减少边缘的“光晕效应”。近几年，均值滤波、加权最小二乘滤波、各向异性扩散滤波等已被应用到红外线和可见光图像融合中。2007年，Pop S等[3]将偏微分方程引入图像融合，提出了基于PDE的图像融合算法，取得较好的融合效果，但在平滑过程中会丢失重要信息，因此融合图像边缘保持不好。2016年，Durga等[4]提出基于二阶PDE的各向异性扩散滤波与传统的PCA结合的融合算法，融合图像边缘保持不好。2017年，Durga等[5]又将二阶PDE滤波改进为四阶PDE滤波，视觉效果较好，但出现了少许斑点。文中结合二阶PDE和四阶PDE的优缺点，提出基于PDE的二阶和四阶相结合的自适应滤波器应用于图像融合。

1 PDE自适应滤波器

1.1 一种新的扩散函数

扩散系数可以控制偏微分方程去噪模型的平滑力度，1990年Perona和Malik给出了一种扩散函数[6]：

(1)

(2)

其中，a为[-2,10]内的常数。a取-2和1时不同扩散函数的对比图像见图1。

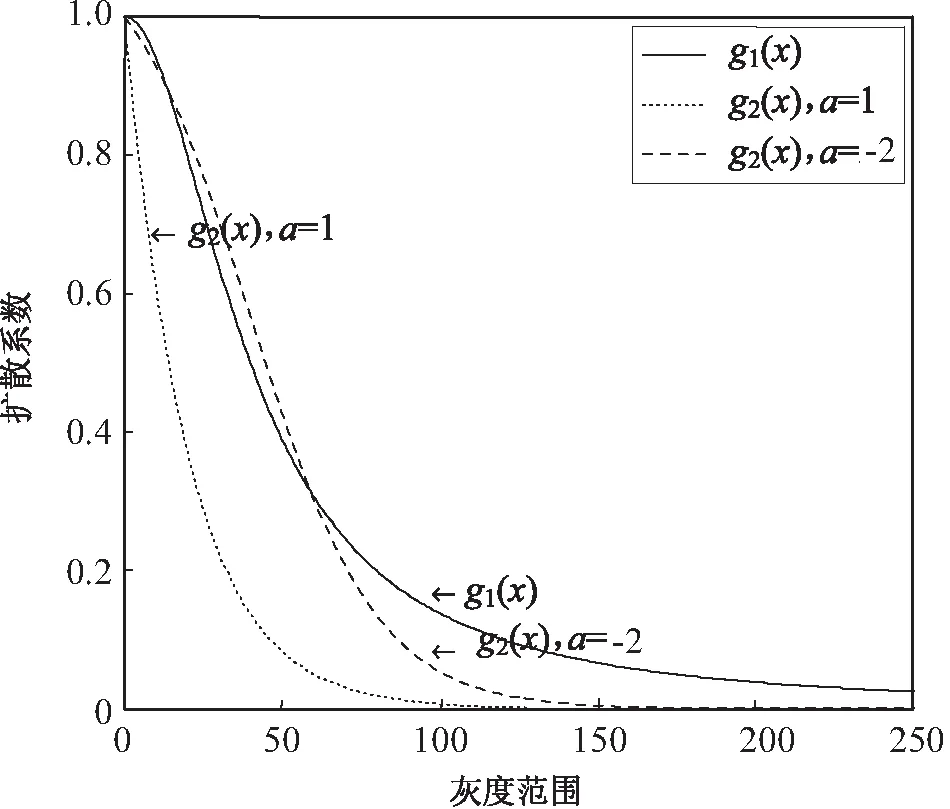
图1 不同扩散函数的图像

由图1可知，当a取较大的数1时，在|u|较小时，即平坦区域，扩散函数g2比g1值大，则可以更大程度地去除噪声；而在|u|较大时，即图像边缘，扩散函数g2相比于g1扩散程度小，能更好地保护图像边缘信息。而当a取较小的数-2时，提出的扩散函数g2平滑速度要比g1快很多，能够更快地达到最优结果。

综上分析，对于不同图像平滑，扩散函数g2可以通过a调节扩散函数的平滑力度，从而得到更加好的平滑效果。

1.2 自适应扩散模型

1.2.1 PM扩散模型

1990年Perona和Malik提出了P-M扩散模型[6]：

(3)

虽然二阶“PM扩散模型”在平滑图像的同时可以保护边缘，但在图像平滑区域容易出现过度平滑，从而产生“阶梯效应”。

1.2.2 YK扩散模型

为了克服“阶梯效应”，2000年You和Kaveh提出了四阶偏微分方程去噪模型，即YK模型[8]：

(4)

该模型用拉普拉斯算子代替梯度算子，消除了“阶梯效应”，但是不能很好地保护边缘且有黑色斑点产生。同时Y-K模型的去噪效率和边缘保护能力都不如二阶PM模型。

1.2.3 自适应扩散模型

2009年，刘小扬等提出了二阶和四阶相结合的PDE模型[9]：

(5)

其中，w1，w2是权系数，且w1+w2=1。引入|u|限制|2u|产生的孤立点，消除了“斑点效应”[10]，但边缘保持不好。

因此，结合二阶和四阶模型的优缺点，提出了二阶四阶相结合的自适应扩散模型(见图2)：

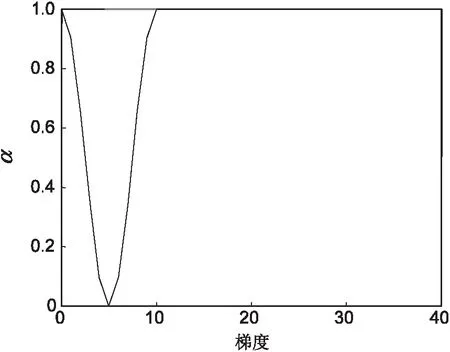
图2 α随梯度变化曲线

(6)

其中

(7)

模型通过α控制扩散系数，在图像渐变区域(梯度值为中间值)，α取较小值，即通过高阶模型进行平滑，从而避免“块状效应”；而在图像平滑区域(梯度值较小)和梯度突变区域(梯度值较大)[10]，α取较大值，即通过低阶模型进行平滑，从而达到去噪的同时保持边缘。因此，新模型可以自适应地在不同区域选择不同的扩散函数，有很好的边缘保护效果。

2 基于非线性模型的图像融合

2.1 自适应滤波器分解

边缘保护滤波器可以将源图像分解为一个平滑的基础层和多个细节层，分解之后的图像能够保持源图像的空间一致性。源图像In(x,y)通过“自适应滤波器”分解为细节层Dn(x,y)和基础层Bn(x,y)[4]，再通过不同的融合规则进行融合，得到最终融合图像。图像融合方案如图3所示。

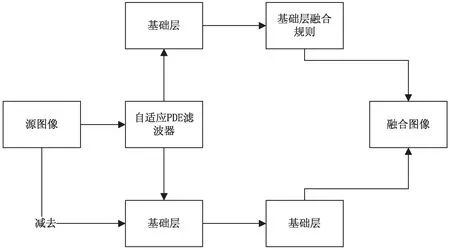
图3 图像融合方案

源图像In(x,y)通过“自适应PDE滤波器”平滑得到基础层图Bn(x,y)和细节层图Dn(x,y)[4]：

Bn(x,y)=PDE (In(x,y))

(8)

Dn(x,y)=In(x,y)-Bn(x,y)

(9)

2.2 细节层融合规则

LDA是基于总体参数的非鲁棒性，因此对异常值比较敏感[11]，这里引入中值LDA鲁棒算法。

将两幅细节图像D1(x,y)和D2(x,y)写为矩阵X的列向量[4]，计算矩阵C的本征值σ1、σ2和本征向量ξ1、ξ2，则

(10)

细节层图像的权重为：

(11)

其中，ξmax(i)为矩阵C最大特征值对应的特征向量。

(12)

2.3 基础层图像融合

(13)

最终融合图F为：

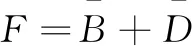
(14)

3 融合实验和性能分析

3.1 参数选取

边缘保持度QAB/F采用Sobel边缘检测原理[12]，能准确计算出融合图像中有多少源图像的边缘细节信息，定义为:

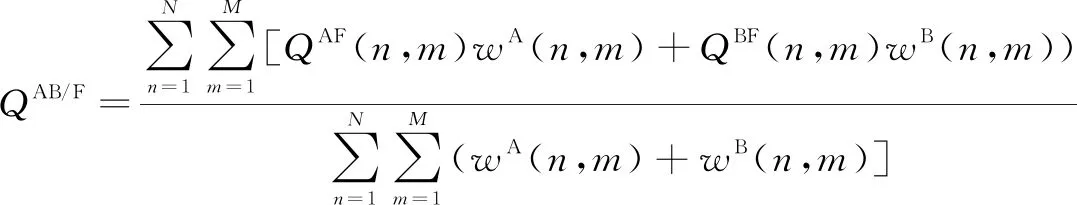
(15)

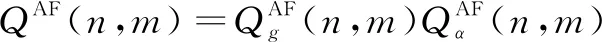
引入QAB/F作度量，选取已配准的clock多聚焦图像进行参数选取仿真实验，如图4所示。其中QAB/F最大时得到最佳参数，则文中算法的最佳参数为：迭代次数n=9、阈值k=20和步长h=0.1。选取最佳值k时，设定n=20,h=0.1；选取最佳值n时，设定k=20,h=0.1；选取最佳值h时，设定k=20,n=20。

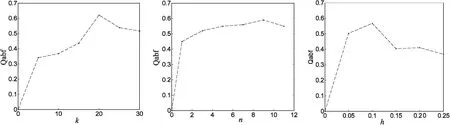
图4 最佳参数选择图

3.2 融合图像主客观评价

为了验证文中算法的有效性，将文中算法与经典加权平均算法和传统小波算法进行比较，如图5所示。从主观视觉来看，加权平均对源图像的基本信息丢失比较明显，传统小波和文献[3]源图像的基本信息保留比较好，但还不够清晰，而基于文中算法的融合图像明显比较清晰。

为了更进一步验证文中算法的优越性，选取空间频率SF、标准差SD、边缘保持度QAB/F以及结构相似度SSIM等客观评价指标与经典算法加权平均、小波以及文献[3]算法进 行比较，指标越大，融合效果越好。各指标定义如下：

(1)SSIM定义如下：

(16)

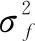
图5 clock原始图与融合结果图

(2)SF主要反映图像的总体活跃度[13]，它的值越大，图像越清晰。

定义为：

(17)

其中，RF和CF分别表示图像空间的行频率和列频率：

(18)

(3)SD反映了各个像素点处的灰度离散分布情况，其值越大，图像包含的信息量越多，融合效果就越好[14]。

定义为：

(20)

其中

(21)

客观融合指标对比见表1。

表1 客观融合指标对比

4 结束语

依据非线性偏微分方程在同质区域平滑处理图像时能很好地保护图像的边缘以及低高阶PDE的优缺点，提出了一种二阶和四阶PDE相结合的自适应分解滤波器与LDA相结合的图像融合算法。自适应分解滤波器根据图像的局部特征对图像进行不同程度的扩散，很好地保护了边缘。

实验结果表明，融合图像较好地保留了源图像的边缘信息。