入射条件对射弹入水跳弹行为的影响研究

陈国明，胡俊华，刘 安，冯金富，李永利

(1.空军工程大学 航空工程学院，陕西 西安 710038；2.武警工程大学 装备工程学院，陕西 西安 710086)

0 引 言

近年来，随着各学科的不断交叉融合，在新任务需求的牵引下，越来越多的国家和研究者开始关注潜-飞两栖导弹和水空跨介质航行器，其主要特点是兼具空中飞行和水下潜航双重功能，且能够多次在空气、水介质中穿梭飞行[1-2].潜-飞两栖导弹使用弹跳入水方式，多次在空气和水两种介质中穿梭弹跳飞行，躲避物理上割裂的空中雷达网和水下反潜网，有利于突防敌方的防御.廖保全等[3]提出了一种通过两次折叠弹翼改变外形以实现水空介质跨越的射弹平台，其兼顾空中突防速度快和水中突防隐蔽性好的特点.射弹在水中航行时，采用类似鱼雷的外形，在空中飞行时，采用类似反舰巡航导弹的外形，如图 1 所示.这种折叠方式减小了弹翼折叠过程中机体重心的变化，降低了出水控制难度.张佳强[4]对一类潜-飞两栖新概念导弹进行研究，基于可伸展环形翼构想，提出了一种共形半环翼布局的潜-飞两栖导弹概念方案，如图 2 所示.文献中阐述了其水-空介质适应性设计的原理，分析了技术方案的可行性，并采用ANSYS CFX软件数值模拟了导弹空中构型在设计速度下的气动特性和水动特性，验证了方案设计的两种构型和采用变体技术实现构型间相互转换的必要性和合理性.

图 1 两次折叠弹翼型跨介质射弹概念Fig.1 The concept of trans-media projectile with twice folding wing

图 2 共形半环翼布局跨介质射弹概念方案Fig.2 The concept of trans-media projectile based on conformal semi-ring wing

跳弹行为很早就被运用到军事领域，二战期间海军火炮手通过跳弹行为拓展了加农炮的攻击范围，Barnes Wallis 系统地研究了这个现象并发明了水面弹跳炮弹，之后英国专门研发了一种弹跳炸弹成功摧毁了德国在鲁尔河上的水坝[5-6].自此之后，专家学者们提出很多入水跳弹模型.Xu等[7]基于能量损失提出了一种跳弹行为的新定义，并通过实验和仿真方法预测了出射速度和出射角度；李永利等[8]研究了射弹的不同头型和密度对入水过程的影响，分析了跳弹过程中速度等参量的变化量，并提出一种截头型射弹构型来抑制鱼雷等水下兵器入水时的跳弹行为；齐铎等[9]研究了不同初始条件对空投自主式水下潜航器(Autonomous Underwater Vehicle, AUV)入水的影响，得到了速度和压力响应曲线，并建议应避免垂直入水，为空投水下兵器等行为提供了一定的借鉴意义.

本文利用ANSYS CFX软件构建射弹的入水数值计算模型，分别以入射角度和入水速度为变量，对射弹跳弹过程进行数值模拟.首先对射弹小角度入水过程进行数值仿真，得到了跳弹行为的全过程，并对整个跳弹过程进行了分析；然后以入水速度为变量进行仿真计算，研究了入水速度对跳弹的影响；最后改变入射角度进行数值模拟，分析了入射角度对跳弹的影响.

1 数值计算模型

1.1 物理模型[10]

本文研究对象为总长度l=533 mm，质量分布均匀，头部为30°顶角的尖拱体形状，尾部为线性截断的回转圆柱体射弹，其结构简化图如图 3 所示，其中顶角α=30°，扫掠角β=30°，rt为扫描半径，最大直径D=53.3 mm，尾部长度lt=60 mm，尾部最小直径dt=26.65 mm.

图 3 射弹几何尺寸Fig.3 Geometric parameters of the projectile

1.2 初始设置

射弹头部与水面距离为2D，为仿真软件提供初始化时间，提高计算可靠性和精度.射弹入水初始状态如图 4 所示.

图 4 数值仿真初始状态Fig.4 Initial condition of numerical simulation

在仿真实验中，作如下假设：① 射弹是质量分布均匀的刚体；② 水介质为不可压缩液体；③ 温度变化忽略不计；④ 入水瞬间初始攻角为零.

2 仿真结果分析

2.1 射弹入水跳弹行为

首先模拟入水速度为20 m/s和入射角度为15°的工况下射弹入水的跳弹行为，整个入水过程如图 5 所示.由图可以清晰地看出跳弹的全过程，其中介面上下分别代表空气相和液体相，仿真较好地模拟了射弹伴随入水过程出现的气垫、溅水、水面隆起等现象.起始时间和终止时间分别为 0.04 s 和0.4 s，相邻两组图片的时间间隔为 0.04 s.

图 5 射弹入水跳弹全过程Fig.5 The whole process of ricochet behavior

射弹最初在空中飞行，只受重力和空气阻力作用，倾斜角几乎不发生变化.在射弹头部顶端还未接触水面之前，由于气垫作用，水面产生一个“凹陷”.随着头部开始入水，由于撞击作用，射弹受到作用于沾水面的巨大冲击载荷，又因撞击作用时间短和沾水面积小，射弹的运动状态改变量不大.同时，原本平静的液体自由表面开始形成流动，产生喷溅和溅水现象，射弹头部附近的水介质被抬起，间接增大了沾水面积和入水深度.随着入水的继续，射弹的沾水面上受到比撞水峰值小得多的侵水阻力，由于作用时间长且沾水面积大，产生的冲量和冲量矩也比较大，射弹姿态角持续发生改变，水下弹道向上弯曲.后射弹头部逐渐出水并离开水面，由于尾部受到的上下两部分水的作用力不对称，使其产生向上的转动力矩，使射弹完全离开水面.

通过上述分析，可将射弹入水过程的跳弹行为分成3个阶段[11]：撞水阶段、侵水阶段和出水阶段.撞水阶段：射弹撞击水面，头部沾水处受到巨大的冲击载荷作用，可能使局部损坏或者内部器件失灵，由于持续时间短和浸湿面积小，所以总的冲量相对较小，对射弹整体运动产生的影响不大，但是可能引起浸湿处出现局部破坏.侵水阶段：随着入水深度的增加，沾水面积变大，射弹的一部分动能转换为水的动能使水产生流动，其水下姿态和倾斜角发生较大的改变，这个阶段射弹受到的力比峰值小得多，但是作用时间和沾湿面积也大得多，因而产生的冲量要比撞水阶段大得多，射弹姿态改变最大.出水阶段：射弹倾斜角在自身剩余动能和水的共同作用下继续减小，射弹头部开始离开水面，在其上表面的水的重力作用下继续出水，直到完全离开水面.

2.2 入水速度对跳弹行为的影响

为了研究初始入水速度对射弹跳弹行为的影响，分别对初始速度为10, 20, 30和40 m/s等4种工况下的射弹入水过程进行研究，其中初始倾斜角为15°.

由于初始速度不同，4种工况下的出水状态选择的时间分别为0.6, 0.4, 0.3和0.3 s.从图 6 中可以看出，4种工况下，10 m/s初始速度下的射弹在0.6 s还未出水，其他工况下的射弹已经开始离开液面，其中40 m/s初始速度的射弹的1/3已经离开了水面，尾部还有一个闭合的空泡.由此可知，初始速度是跳弹行为的重要影响因素之一，初始速度越大，在小角度下发生跳弹行为的可能性越大而且越容易.同时可以推测，当初始速度较小时，射弹所具有的初始动能不足以使其跃出水面产生跳弹行为.

如图 7 所示，整个入水过程中，不同初始速度下，射弹的运动都经历了角速度的快速降低，但是初始速度越大，角速度阶跃式减小的幅度越大，发生角速度突变的时间越早.证明了跳弹过程第2阶段角加速度和角速度发生阶跃式减小的必然性.

图 6 射弹不同速度入水的终止状态Fig.6 The final condition of water-entry

图 7 不同入水速度下角加速度和角速度随时间变化曲线Fig.7 The changes of angular acceleration and angular velocity at different velocities of water-entry

如图 8 所示为不同初始速度下入水射弹质心的位移随时间变化的曲线.

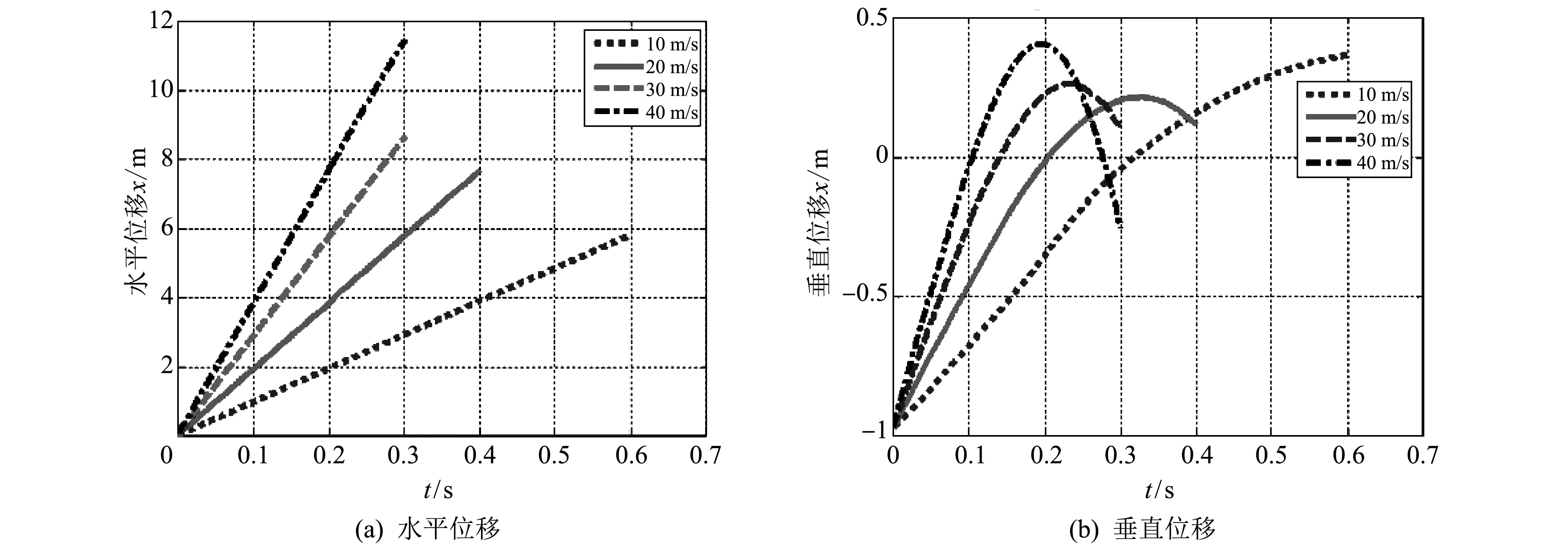
图 8 不同初始速度下入水射弹质心位移随时间变化的曲线Fig.8 The changes of displacement for barycenter of projectile at different initial velocities

图8(a)中，4种初始速度下，入水射弹质心的水平位移与时间呈现简单的线性关系，表明水平方向的速度基本保持不变.图8(b)给出了4种初始速度下，射弹质心在垂直方向的位移随时间变化的曲线，其中负值表示射弹质心还在自由液面之上.从图中可以发现，初始速度为20, 30和40 m/s 时，射弹质心在垂直方向上都发生了“反向”运动，而且初始速度越大，垂直方向的位移越大，发生“反向”运动的时间越早.当初始速度为 10 m/s 时，射弹质心的位移一直在增大，并且增大的趋势越来越小.由此可以推测，当初始速度较小时，射弹所具有的初始动能不足以使其跃出水面而产生跳弹行为.

2.3 入射角度对跳弹行为的影响

为了探究射弹的跳弹行为与入射角度的关系，对比多角度下射弹的入水过程，计算了初始倾斜角度为 15°, 30°和 45°情况下射弹的入水过程，初始速度均为 20 m/s.射弹在不同初始倾斜角度下的入水情况如图 9 所示.

图 9 射弹在不同初始倾斜角度下入水情况Fig.9 The results of water-entry at different initial angles

在15°入水工况下，射弹在0.4 s已经产生跳弹行为，因此另外两种角度下的入水也以0.4 s为终止时间.整个运动过程中，射弹的倾斜角度变化量如表 1 所示.

由表 1 可知，3种入射角度下的入水过程中，射弹的倾斜角度都发生了较大的变化，尤其以15°入射角度下的入水变化最大，随着初始倾斜角度的增大，角度的变化量越来越小.因此，可得出结论，在入射角度为0°～45°内必然存在着一个初始的临界入水倾斜角，使入水的射弹发生跳弹行为.

表 1 不同入射角的入水过程中的角度的变化量

图10(a)中，3种入射角度的射弹在入水第一阶段的角加速度的变化趋势基本一致，初始基本为零，然后在一个时间段内迅速增加，达到峰值之后迅速减小，最后保持在一个平稳的值.由于三者初始的位置差异，因此射弹入水的时间不同，角加速度峰值产生的时间点也不一样.入水角度为15°, 30°和45°的峰值分别在0.039, 0.053和0.056 s 出现，而15°入水的角加速度峰值分别是30°和45°的2倍和3倍.由此可见，入射角度越小，射弹入水初期受到的冲击越大.

图10(b)中，3种入射角度的射弹入水之后加速度随时间的变化规律也基本一致，唯一的差别是15°初始倾斜角度的射弹在入水0.37～0.39 s内，其角速度迅速降低，而另外两种入水角度下的射弹在该时间段并没有发生角速度的突变，其趋势只是缓慢地减小.

经过对不同入水倾斜角度下角加速度和角速度随时间变化规律的分析，基本可以初步推测小角度下射弹入水发生跳弹行为极有可能与入水初期的角加速度峰值大小和后期的角速度突变有很大的关系.

图 11 分别给出了不同入水倾斜角度下入水射弹质心的水平和垂直方向的位移随时间的变化曲线.

从图11(a)中可以看出，3种初始角度的入水中，射弹质心在水平方向的位移与时间的变化曲线基本呈线性递增关系，并且初始角度越小，水平方向的位移越大，这与水平方向的初始速度分量最大有关系.图11(b)中，30°和45°入射角度下，射弹质心垂直方向的位移曲线的斜率逐渐趋于平缓，只有15°入射角度的位移先增大后逐渐减小，再次显示了射弹跳弹行为运动过程的本质.

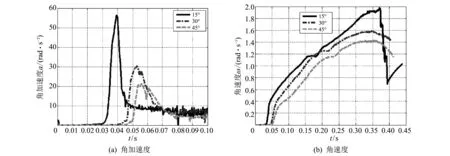
图 10 不同入水速度下角加速度和角速度随时间变化曲线Fig.10 The changes of angular acceleration and angular velocity at different velocities of water-entry

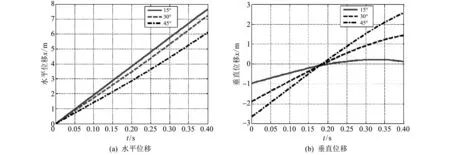
图 11 不同初始倾斜角入水射弹质心水平和垂直位移Fig.11 The changes of horizontal and vertical displacement for barycenter of projectile at different initial angles

3 结 论

本文利用数值仿真的方法，研究了射弹初始条件对弹跳入水的影响.以入水速度和入射角度为变量，得到了入水全过程，分析了水下轨迹、角加速度、角速度和位移变化曲线，得到如下结论：

1) 射弹入水过程中发生的跳弹现象可以分成3个阶段：撞击阶段、侵水阶段和出水阶段.

2) 相同入射角度下，入水速度越大，射弹越容易发生跳弹行为，且发生跳弹的速度越快.对于较小的入水速度来说，虽然射弹的入水轨迹也发生了向上弯曲，但由于动能的不足，使其无法离开水面.

3) 相同入水速度下，射弹入射角度越小，越容易发生跳弹行为，角度改变量越大，初始时刻角加速度的变化越剧烈，角加速度的峰值也越大.