带有对数非线性项的p-Kirchhoff型方程的多解性

段碧霄，王淑丽，郭祖记

(太原理工大学 数学学院，山西 太原 030024)

0 引 言

Kirchhoff型方程在很多数学物理现象以及生物系统的研究中都起着重要作用, 如弹力绳的振动现象, 种群密度等.国内外很多学者对Kirchhoff型方程进行了研究, 并得到了许多重要结果[1-6].对于如下Kirchhoff型方程

式中：λ>0, 文献[7]研究了当函数M,f满足不同条件时方程解的存在性问题.此外, 还有很多关于p-Kirchhoff 型方程的研究[8-10].

近来, 学者多研究带有对数非线性项的偏微分方程, 但是仍然没有对带有对数项的p-Kirchhoff型方程的研究[11-12].受以上工作的启发, 本文利用山路定理和Ekeland 变分原理研究方程

(1)

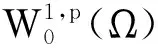
本文主要结果如下:

定理 1 假设存在非空开区域Ω1⊂Ω满足g(x)>0, 存在λ0>0, 当λ∈(0,λ0)时, 方程(1)至少有两个非平凡解.

本文第1部分主要介绍了对数不等式以及证明定理1用到的一些估计, 第2部分则用山路定理和Ekeland变分原理证明了定理1.

1 预备知识

其中

(2)

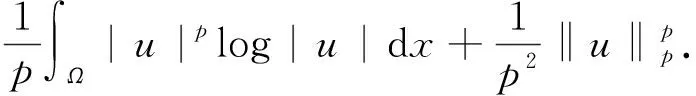
(3)

〈J′(u),v〉=

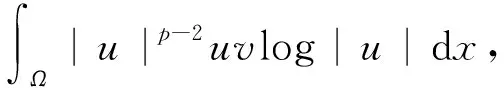
(4)

则方程(1)的弱解就是泛函J的临界点.

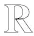
a) 存在ρ,α>0, 当‖u‖=ρ时，J(u)≥α;

定义

Γ={γ∈C1([0, 1],E)|γ(0)=0,

记

于是J关于c存在临界序列, 若J还满足(PS)条件, 则c是J的临界值.

2 定理1的证明

引理 3 存在ρ,α>0使得当‖u‖=ρ时,J(u)≥α.

证明 由Hölder不等式和Sobolev不等式有

(5)

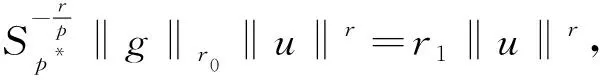
(6)

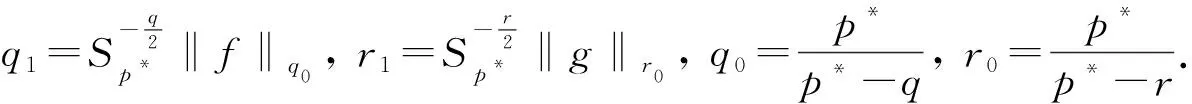
(7)

其中,

直接计算有

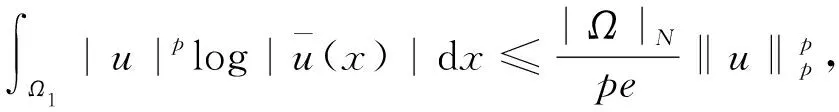
(8)

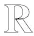
结合式(7)有

(9)

令μ=a>0, 由式(3), (5), (6)和(9)有

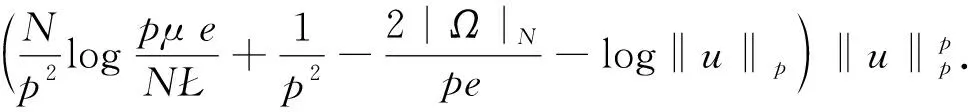
(10)

令h(z)=λq1zq-2p+r1zr-2p, 则h(z)→∞,z→0+或z→+∞, 则h(z)在z1>0处有一个极小值z1.直接计算有

h′(z)=λq1(q-2p)zq-2p-1+r1(r-2p)zr-2p-1.

(11)

因此, 存在λ1>0, 当λ∈(0,λ1)时有式(11)成立.存在λ2>0, 当λ∈(0,λ2)时,

则对t>0有

引理 5J(u)满足(PS)条件.

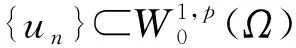
J(un)→c,J′(un)→0.

(12)

首先证明{un}有界.对任意的t>0,p0使得

|tplogt|≤Cι(|t|p-2+|t|p+t-2)

(13)

成立.由式(13)和Sobolev不等式有

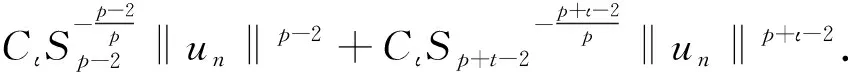
(14)

结合式(5), (6)和(14)有

(15)

则存在{un}的子列, 仍记作{un}, 使得式(15)成立.由Hölder不等式有

成立, 从而

(16)

同理有

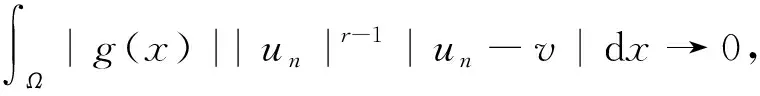
(17)

(18)

又因为J′(un)→0, 所以有〈J′(un),un-v〉→0, 其中

〈J′(un),un-v〉=

结合式(16)～(18)有

n→∞.

此外, 由式(15)知

n→∞，

从而

因此‖un-v‖→0,n→∞.故J(u)满足(PS)条件.

成立, 则对引理3中ρ>0有

从而对任意的εn>0有

(19)

cρ≤J(un)

(20)

J(un)

(21)

结合式(19)～(21)可得

故有{un}∈Bρ.

Φ(u)=J(u)+εn‖un-u‖,

令t→0+, 有

〈J′(un),v〉+εn‖v‖≥0,

用-v代替v可得-〈J′(un),v〉+εn‖v‖≥0, 故有‖J′(un)‖≤εn.

因此, 存在序列{un}⊂Bρ使得J(un)→cρ<0,J′(un)→0, 则cρ可达.