木构建筑的抗振动模型设计与仿真*

曹艳玲， 袁义宏

(华南理工大学 a. 建筑学院， b. 设计学院， 广州 510009)

地震灾害自古以来就对人类构成了巨大的威胁.自近一个世纪，我国多处遭受了地震灾害，造成了众多人员伤亡及巨大财产损失[1-3].

中国木构建筑结构自古代起，以其独特性，进行了几千年的传承演变，在广大地区广为传播，形成了独具特色、博大精深的建筑体系，成为东方建筑文化的代表[4].然而由于各种原因，很多古代木构建筑荡然无存，只有一小部分的木构古建筑遗产保存较好.随着岁月流逝，木构古建筑的破坏也日趋严重，加上地震等自然灾害的影响，使得保护、加固和维修这些木构古建筑迫在眉睫[5-7].由于古代木构建筑在我国古代建筑上占据着主要地位，其防震技术是非常独特的，对其进行抗振动模型设计，对于研究木构建筑具有重要意义[8].

文献[9]对混凝土剪力墙结构底部4层1/2比例空间模型进行低周反复荷载试验，通过该试验得出装配式混凝土剪力墙结构抗震性能满足我国抗震设防要求，但该方法对填充墙主体结构强度和刚度的影响考虑不够充分，导致所得结果可信度不高.文献[10]提出带有斜撑的钢桁架数值简化分析及抗震性能分析模型，该方法可靠性较高，但方法应用过程却具有较大难度，故无法得以广泛应用.

针对上述问题，提出一种新的建筑抗振动模型设计方法，并将其使用到木构建筑.本文首先分析木构建筑材料性质和静压本构关系，确定木构建筑结构关系；其次分析木构建筑结构体系及其在振动时的自振频率与振型，为建立木构建筑的抗振动模型提供依据；最后在确定振型的基础上，给出产生振动时的动力方程，在考虑建筑自身的稳定性及抗振动限值的情况下，建立木构建筑的抗振动模型.实验结果分析表明，采用本文设计的抗振动模型比传统的抗振动模型更能体现出木构建筑的抗振动性能.

1 木构建筑结构关系分析

在对木构建筑结构关系进行分析时，主要通过两方面进行：一方面是木构建筑材料性质的分析；另一方面是木构建筑材料静压本构关系的分析.

1.1 木构建筑材料形变分析

木材是木结构古建筑的主要建筑材料，由于建筑结构的特点，在物理性能方面存在各向异性特征，木材顺纹强度最高，横纹强度最低，斜纹强度在两者之间.木材的强度与取材部位有着紧密的联系，也与含水率、负荷持续时间、温度等因素相关.没有缺陷的木材和有缺陷的木材之间力学性质区别较大.

在发生相对较小的变形时，木材可能会突然产生拉伸及剪切破坏，这属于脆性损坏.木材受到压缩及弯曲破坏较大，产生不可逆的塑性变形特性，其抗压强度比抗拉强度低.木材受弯强度介于二者之间，可描述为

(1)

式中：fts、fcs、fms分别为木材标准试件的受拉、受压及受弯强度；G为木材受拉、受压及受弯时的权重.

1.2 木构建筑材料静压本构关系分析

(2)

式中：EL为木材处于线弹性阶段时的弹性模量；ET为木材处于应变弱化阶段时的切线模量；σL为木材原始疏松组织线弹性阶段时的应力；εL1为木材进入塑性流动阶段时的应变；εL2为木材进入应变弱化阶段时的应变；εn为木材被压实时的应变；σn为木材被压实时的应力.

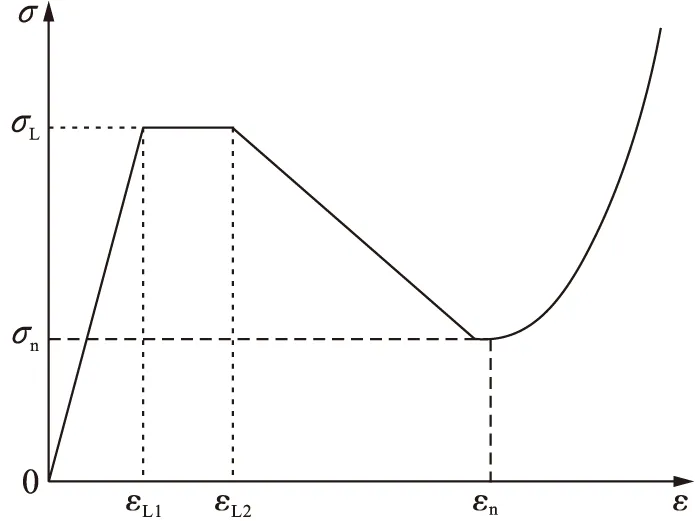
图1 木材静压的本构关系Fig.1 Constitutive relation of wood under static pressure

2 木构建筑抗振动模型建立

2.1 木构建筑结构及振动模型设计

在分析木构结构本构关系的基础上，需要分析木构建筑结构体系及其在振动时的自振频率与振型，可为建立木构建筑抗振动模型提供科学依据.

假设木构建筑的结构总刚度矩阵为K，总质量矩阵为M，总阻尼矩阵为C，总节点位移(列)矩阵为δ(t)，则建筑的多自由度体系振动方程为

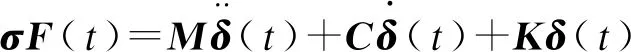
(3)

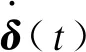
(4)

式中：Ki、Mi、Ci和δ(t)i为元素i上的刚度矩阵、质量矩阵、阻尼矩阵和节点位移(列)矩阵；B为单元应变矩阵；D为与单元木构材料有关的弹性矩阵；N为木构材料的单元形函数矩阵；ρ、c为单元木构材料的质量密度和粘滞阻尼系数.假如木构建筑的结构作简谐振动，则总节点位移(列)矩阵可表示为

δ(t)=gsinωt

(5)

式中：g为δ(t)的振幅列向量，与时间t无关；ω为建筑结构的固有频率.当ω和非零向量g满足Kg=ω2Mg时，ω和g分别称为广义特征值和广义特征向量.

以木构建筑自振频率为基础，确定木构建筑的振型可表示为

f(t)=-λRdsinωt

(6)

式中：Rd为木材直径；λ为建筑物自振频率.

2.2 构建木构建筑抗振动模型

在确定木构建筑地震时的振型后，构建木构建筑抗振动模型.假设发生强度为I级地震时，其建筑结构的失效概率为P(LS/I)，则此木构建筑在振动时某一极限值概率为

PLS=z(t)∑P(LS/I)P(I)

(7)

式中：P(I)为发生地震强度为I级的概率；z为地震振动函数.由于地震对木构建筑的振动是连续的，因此将其表示成积分形式为

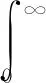
(8)

式中：F(m)=P(LS/I=m)；G(x)=P(I≥m)为发生地震强度大于或等于m的概率.若使用震级频度关系来表示地震大小间的关系，则lgU(V)=a-bV时，可确定地震振动衰减关系或烈度衰减关系，可表示为

lnA=C1PLS+C2O+C3ln(Rd+R0)

(9)

I=C1lnA+C2O+C3ln(Rd+R0)

(10)

式中：A为加速度、速度或位移；O为震级；C1、C2、C3、R0为统计常数.木结构建筑在地震作用下，可发生的位移与耗能的数值大小可表示建筑的破坏情况，即

(11)

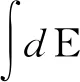
(12)

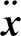
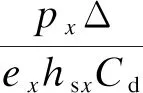
(13)

(14)

式中：px为x水平和以上整体的竖向设计荷载；hsx为x水平及以下的建筑高度；γ为层间剪切应力值域真实抗剪承载力值比；Δ为层间位移；Cd为位移增大系数；ex为修正系数.建筑抗振动性主要由地震需求D和建筑结构抗振能力C的比值决定的，且D与C两者均服从对数正态分布，由此可推出木构建筑的抗振动模型为

(15)

3 实验结果分析

由图2～4可知，在时间不定的情况下，采用文献[9]模型时，出现的波动整体较为稀疏，但稳定性很差；采用文献[10]模型时，一开始就出现强烈的波动，峰值不高，但在4 s之后，出现的波动虽然较为稀疏但其峰值增高，不适合使用；采用本文模型时，其刚出现振动时，抗振性能很好，未出现位移波动，随着振动时间的增长，出现了少量的波动，虽然在4 s左右出现了很高的峰值，但是随后便开始降低，整体性能要优于文献[9]与[10]模型，具有一定的优势.这是因为本文建筑抗振动模型考虑了建筑自身的稳定性和抗振限值，而传统方法建模时，仅仅考虑了建筑结构自身的稳定性，而未考虑建筑材料自身的结构与稳定性能.在进行不同方法所构模型测试时，本文模型较其他模型能显示出更好的稳定性.

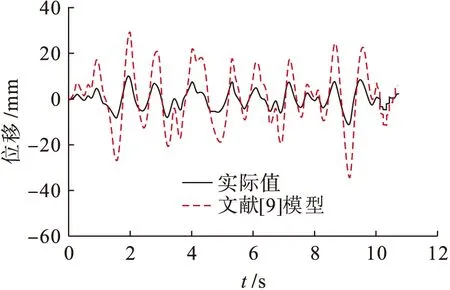
图2 文献[9]模型性能Fig.2 Model performance from literature [9]

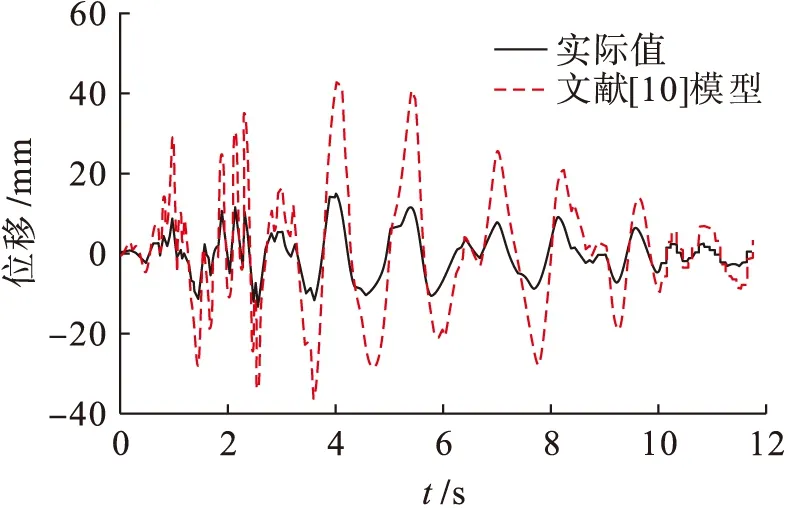
图3 文献[10]模型性能Fig.3 Model performance from literature [10]

图4 本文模型性能Fig.4 Model performance of this work

为进一步验证本文模型在抗振动性能方面的有效性及可行性，分别将文献[9]、[10]模型与本文模型进行对比，在位移不定的情况下，对比了建筑承受荷载情况，结果如图5～7所示.

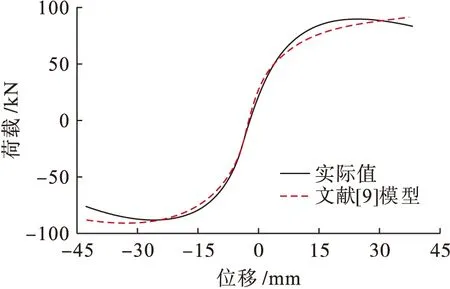
图5 文献[9]模型对比图Fig.5 Comparison of model in literature [9]

图6 文献[10]模型对比图Fig.6 Comparison of model in literature [10]

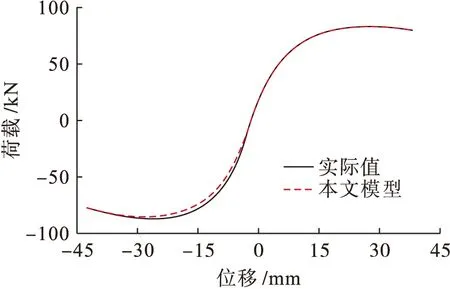
图7 本文模型对比图Fig.7 Comparison of model of this work

由图5～7可知，整体上实验值与实际值基本接近，在振动开始时处在弹性阶段，全部恢复力曲线在开始时就处在直线状态，随着加载进程的实行，模型进入弹塑性阶段，加载和卸载刚度随着循环次数的增加而显著降低.文献[9]与[10]模型在实验过程中，由于建筑自身的不对称性和正反方向破坏形态的不对称性等，导致左右两端承载力有稍微差别.而本文方法由于充分考虑了木构建筑材料性质，尤其考虑了木构材料的弹性形变及其自身的静压本构关系，最终保证了所建模型的稳定性及准确性.

4 结 论

针对传统的建筑抗振动模型分析一直存在建模不准确的问题，提出一种新的建筑抗振动模型设计方法.分别对木构建筑材料性质与静压本构关系进行了分析，确定木构建筑结构关系；分析木构建筑结构体系及其在振动时的自振频率与振型，为建立木构建筑的抗振动模型提供依据；在确定振型的基础上，给出产生振动时的动力方程，在考虑建筑自身的稳定性及抗振动限值的情况下，建立木构建筑的抗振动模型.实验结果表明，本文设计的抗振动模型要比传统的抗振动模型稳定性更高，与实验值差异性较小，更能体现出木构建筑的抗振动性能.