考虑主梁损伤的装配式梁桥荷载横向分布系数计算

李院军，邬晓光，黄成，肖凯龙，殷悦

考虑主梁损伤的装配式梁桥荷载横向分布系数计算

李院军，邬晓光，黄成，肖凯龙，殷悦

(长安大学 公路学院，陕西 西安 710064)

为了计算在役装配式梁桥发生主梁损伤情况下的荷载横向分布系数，以12座装配式T梁和小箱梁桥为背景，通过实桥荷载试验数据，得出荷载横向分布系数实测换算值；同时考虑竖向基频、线刚度和宽跨比3个关键因素，引入一个主梁损伤折减系数β，通过matlab软件多元非线性回归分析法拟合，得到一种考虑桥梁受力性能的荷载横向分布系数的计算方法，并与实桥数据、有限元法(ANSYS)及传统计算方法的计算结果进行对比。研究结果表明：考虑主梁损伤的装配式梁桥荷载横向分布系数的计算方法的计算结果与实桥数据较为接近。

桥梁工程；装配式梁桥；荷载横向分布系数；非线性回归分析

截止2017年底，我国既有桥梁已超过80余万座，其中装配式梁桥占据很大的比例。但随着桥梁建设的加快，其养护却远远跟不上，导致在役的装配式梁桥出现各种不同程度的损伤，亟需对在役桥梁的整体性能进行评估[1]。荷载横向分布系数通常可以反映一座桥的整体受力情况。目前，修正偏心压力法、刚接梁法和G-M法等传统荷载横向分布系数计算方法主要针对没有发生损伤的结构，对于在役且出现不同损伤的桥梁，其约束条件、刚度和横向联系等都发生了改变，若继续沿用上述方法，则会出现计算结果与实际情况失真的情况[2−4]。目前，国外设计规范中，美国AASHTO规范通过有限元分析提出简化荷载横向分布系数公式AASHTO LRFD，日本《国有铁道混凝土结构设计标准解说》按照窄桥与宽桥，把梁桥荷载横向分布系数计算方法分为偏压修正法与GM法[5−9]。国内一些学者也做了相应的研究，刘华等[10]通过考虑固有频率、振型与模态质量，提出一种荷载横向分布系数计算方法。李国豪等[11−17]对梁桥T梁、箱梁和板梁在计算荷载横向分布系数时，主梁的间距、斜交角、横向连接情况等进行了研究。韦立林等[18]通过实测主梁挠度建立实测挠度值与荷载横向分布系数的关系。然而，上述研究主要针对的是桥梁设计阶段，没有考虑桥梁的实际损伤情况，且计算都采用有限元模型模拟，缺乏实桥数据支撑。本文针对在役装配式梁桥荷载横向分布系数进行研究，通过实桥荷载试验数据，并同时考虑能够反映桥梁结构性能的参数，计算在役梁桥发生主梁损伤情况下的荷载横向分布系数，采用多元非线性回归分析方法对实桥数据进行拟合。提出一种适合于在役装配式T梁、小箱梁桥荷载横向分布系数的计算方法。

1 参数选取与评价指标

1.1 参数选取

桥梁结构的性能往往能够通过力学参数与截面几何特性参数来反映[10]，通过上述学者的研究与资料查询可知，竖向基频尤其是第一阶频率能够体现结构的受力性能与边界约束条件；线刚度能够反映结构的整体刚度情况；宽跨比反映桥梁纵横向的受力情况。因此，本文选取竖向基频、线刚度和宽跨比作为反映桥梁结构性能的关键参数。

在役梁桥中，主梁损伤和湿接缝损伤等都会对荷载横向分布系数产生影响。对于装配式T梁和小箱梁，主梁损伤和湿接缝的损伤通过对线刚度的折减进行考虑。因此，可以得到考虑桥梁损伤的修正荷载横向分布系数计算公式。

本文基于实桥荷载试验数据，同时考虑桥梁损伤对荷载横向分布系数的影响，采用非线性回归分析进行拟合，公式包含竖向基频、线刚度和宽跨比3个关键因素。公式拟合分为2个部分：1) 通过实桥荷载横向分布系数与竖向基频、线刚度、宽跨比和梁所处的位置等参数进行拟合，得到桥梁无损伤情况下跨中截面荷载横向分布系数公式。2) 考虑主梁和湿接缝损伤时的修正公式。

1.2 评价指标

主要针对在役装配式T梁和小箱梁桥，以5座装配式连续T梁桥和7座装配式连续小箱梁桥的荷载试验数据为公式拟合的依据，其力学性能参数与截面特性参数见表1。从表1可以看出，选取桥梁的宽跨比在0.417~1.025之间，主要为宽桥。车辆加载方式为最不利加载，现以报国寺大桥为例，介绍其车辆布载方式和挠度测试点布置。加载车辆为4辆35 t的三轴重车，为偏载布载，并且使控制截面的试验荷载效率满足试验规程的中0.85~1.05的要求。车辆加载示意图如图1所示。

单位：m

表1 桥型及参数组合

注：表格中的线刚度为单片梁的线刚度。

横向分布能力，以各片梁跨中截面挠度值比上各片梁跨中截面挠度值之和作为跨中截面荷载横向分布系数的评价指标[18]，可简化计算出桥梁跨中截面实际荷载横向分布系数：

由式(1)可知，单片梁跨中截面挠度越大，则其受力越大，荷载横向分布系数也越大，根据式(1)可计算出表1中12 座梁桥的跨中截面实际荷载横向分布系数。选取竖向基频、线刚度和宽跨比3个关键的参数，分析其对跨中截面荷载横向分布系数的影响规律。

2 无损伤情况下荷载横向分布系数计算公式拟合

把选取的3个关键参数进行组合，选取合适的函数类型，使其均差与变异系数满足工程进度要求，同时又便于计算。考虑到实际使用中需要计算每一片的荷载横向分布系数，故在此引入一个调节系数，其反映的是各片梁所处的位置和各片梁偏离桥面中心的距离。其表达式如下所示：

式中：为横桥向各片梁位置的调节系数；x为各片梁截面中心到桥面中心的距离；为桥面总宽的1/2。

选取合适的函数后，把3个关键参数和调节系数进行组合，通过matlab软件多元非线性回归分析法拟合，其中i为各片梁的线刚度，因为装配式梁桥是由多片主梁并联而成，故各主梁的线刚度之和为桥梁的整体刚度。拟合的计算公式如下所示：

式中：y为各片梁跨中截面荷载横向分布系数；为桥梁实测第1阶竖向基频；i为各主梁的线刚度；为桥梁宽跨比。

3 损伤情况下荷载横向分布系数修正计算公式拟合

3.1 损伤修正公式拟合

随着桥梁服役年限的增加，在重载交通、温度、收缩徐变和腐蚀等作用下，其主梁和湿接缝必然会出现不同程度的损伤，进而导致桥梁的横向联系减弱，现有的荷载横向分布系数计算方法也就会 失效。

基于主梁和湿接缝的损伤对式(3)进行修正，对于装配式T梁和小箱梁，其主梁损伤和湿接缝的损伤均可通过主梁线刚度折减得以反映，现以5片T梁桥为例，当各梁的线刚度分别为原来的1，2，3，4和5倍，小于1，T梁线刚度示意如图2 所示。

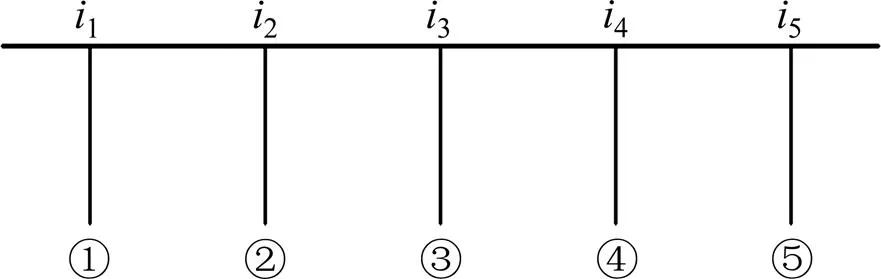
图2 T梁线刚度

由上可得，当各片梁的线刚度分别为原来的1，2，3，4和5倍时，则整个桥的线刚度为：

则考虑主梁和湿接缝损伤后的跨中截面荷载横向分布系数计算公式为：

3.2 主梁损伤折减系数βk的确定

式中：cri为各条裂缝的高度；cri为各条裂缝的间距；cr为裂缝的开裂范围；cri为各条裂缝开展的程度；为裂缝数量。

再由式(8)~(9)和弯矩与曲率的关系，可最终求得开裂截面的损伤刚度：

式中：为在役桥梁某种工况下外力对开裂截面换算截面形心轴产生的弯矩；p为预应力对开裂截面换算截面形心的弯矩。

根据梁段开裂裂缝特性，刚度区间可大致划分为如图3所示。计算桥梁损伤情况下的荷载横向分布系数时，可根据梁段的损伤位置进行损伤刚度区间计算。

图3 梁开裂后刚度阶梯示意

如图3所示，以左边为起点开始计算，通过分段积分即可求得开裂后各段挠度值：

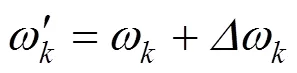
即可用挠度值的变化来反映梁体刚度的折减情况：

由式(10)~(15)，便可最终计算出主梁损伤折减系数：

4 算例分析

以一座多梁装配式T梁桥为例，分别采用荷载试验数据、无损伤情况下多元非线性拟合方法、考虑损伤情况下多元非线性拟合方法、有限元法(ANSYS)及传统计算方法(G-M法和刚接梁板法)计算各片梁跨中截面荷载横向分布系数，并分别与实桥数据进行对比，以验证计算方法的适用性和准确性。

20 m装配式T梁桥，宽跨比为0.75，主梁片数为6片，计算跨径为19 m，梁高1.5 m，单个T梁宽度为2.5 m，桥宽15 m，布置形式为0.75 m+13.5 m(行车道)+0.75 m，双向2车道。截面形式如图4所示，混凝土强度等级为C50。为便于计算，本案例仅考虑主梁跨中区域发生损伤的情况，即可算出梁体发生损伤时的跨中截面荷载横向分布系数，以此来反映主梁损伤后的受力性能。

单位：mm

荷载试验考虑偏载情况下，按照规范加载，具体车辆加载如图5所示，有限元方法、GM法和刚接梁法皆用此加载方式。可根据偏载情况下，实测的各片梁跨中截面挠度值与各片梁跨中截面挠度值之和之比来计算跨中截面荷载横向分布系数，计算公式为式(1)。

ANSYS有限元模型采用SOLID65建模，建立好模型后进行网格划分，加约束边界条件和车辆荷载加载，然后读取每片梁的挠度值进行荷载横向分布系数计算，有限元模型如图6所示。G-M法和刚接梁法按T梁的截面特性和最不利加载便可得到各片梁跨中截面荷载横向分布系数。最终该20 m装配式T梁桥在各种计算方法所得的具体结果见 表2。

单位：mm

图6 ANSYS有限元模型

表2 偏载下不同计算方法所得荷载横向分布系数对比

由表2可得出：1) 对于梁体无损伤情况下，本文方法与实测换算值相比其误差在1%～2%以内，精度符合工程要求，这是由于该方法是以实桥数据为依据，且考虑了线刚度、基频和宽跨比等因素；对于梁体发生损伤情况下，本文方法其最大误差为−1.6%，因考虑了主梁发生损伤的情况，从而导致计算结果偏小，说明在梁体发生损伤时主梁损伤折减系数取值偏大，但误差在允许范围内。2)对于ANSYS有限元法，可见其误差在−1.7%~−3.4%之间，具有较高的精度，验证了模型建立的正确性。3) 对于G-M法其最大误差为4.1%，与刚接梁法相比具有相对高的精度，这是由于G-M法把结构简化成为一块矩形的平板，作为弹性薄板按古典弹性理论来进行分析；对于刚接梁法，其误差范围在2.7%~−6.8%之间，且边主梁误差大于中梁，这是因为刚接梁法的假设是在竖向荷载作用下接合处只传递竖向剪力和赘余弯矩，主梁之间连接为刚接，但是随着桥梁宽度增加，特别是对于大宽跨比桥梁，在偏载作用下边主梁的横向分布能力大于中梁，且荷载横向传递时不能再把主梁之间的连接看成完全的刚接。

5 结论

1) 引入主梁损伤折减系数的概念，并按照主梁开裂裂缝特性，把主梁划分成几个区段，由分段积分计算出挠度值，最终得出主梁损伤折减系数的表达式。该系数可由主梁各区段实际挠度值来反映，实际挠度值越大，主梁损伤折减系数越小，反之则越大。

2) 基于装配式T梁与小箱梁的受力性能特点，选取竖向基频、线刚度和宽跨比为关键因素，以荷载试验的实桥数据为依据，进行多元非线性回归分析拟合，提出一种适用于装配式梁桥荷载横向分布系数的计算方法，为计算梁桥荷载横向分布系数提供参考。

3) 同时考虑到在役桥梁主梁可能发生的损伤情况，对主梁刚度进行损伤折减，得出在主梁损伤情况下装配式梁桥荷载横向分布系数的计算方法。通过实例验证结果表明，该方法能够较好地适用于装配式梁桥荷载横向分布系数的计算，且计算结果较为准确。

[1] 吴向男, 徐岳, 梁鹏. 桥梁结构损伤识别研究现状与展望[J]. 长安大学学报(自然科学版), 2013, 33(6): 49−58．WU Xiangnan, XU Yue, LIANG Peng. Research status and prospect of bridge structure damage identification[J]. Journal of Chang’an University (Natural Science Edition), 2013, 33(6): 49−58.

[2] 邬晓光, 钱若霖, 苏佩. 考虑湿接缝刚度损伤的桥梁荷载横向分布计算方法[J]. 铁道建筑, 2018, 58(1): 93−95. WU Xiaoguang, QIAN Ruolin, SU Pei. Calculation method of lateral load distribution of Bridges considering the stiffness damage of wet joints[J]. Railway Architecture, 2008, 58(1): 93−95.

[3] 王凌波. 在役预应力梁桥残余承载力评估方法研究[D].西安: 长安大学, 2011. WANG Lingbo. Evaluation method of residual capacity of prestressed girder Bridges in service[D]. Xi’an: Chang’an University, 2011.

[4] 赵煜, 周博, 贺拴海, 等. 基于裂缝特征的 PC 简支梁损伤刚度评估方法[J]. 长安大学学报(自然科学版), 2011, 31(4): 39−44.ZHAO Yu, ZHOU Bo, HE Shuanhai, et al. Damage rigidity evaluation method of PC simply supported beam based on fracture characteristics[J]. Journal of Chang’an University (Natural Science Edition), 2011, 31(4): 39−44.

[5] AASHTO LRFD. Bridge design specifications[M]. 4th ed. Washington (DC), 2007.

[6] Mabsout M E, Tarhini K M, Frederick G R. Finite element analysis of steel girder highway bridges[J]. Bridge Engineering, 1997, 2(3): 83−87.

[7] Woo Seok Kim, Jeffrey A Laman, Daniel G. Linzell live load radial moment distribution for horizontally curved bridges[J]. Bridge Engineering, 2007, 12(6): 113− 115.

[8] Khaloo Ali R, Mirzabozorg H. Load distribution factors in simply supported skew bridges[J]. SEI, 2004(5): 55− 57.

[9] EN1992−1−1. Design for concrete structures-Part1: General rules and rules for buildings[S]. European Committee for Standardization, 2002.

[10] 刘华, 叶见曙, 俞博, 等. 桥梁荷载横向分布系数计算方法[J]. 交通运输工程学报, 2009, 9(1): 62−66. LIU Hua, YE Jianshu, YU Bo, et al. Calculation method of horizontal distribution coefficient of bridge load[J]. Journal of Transportation Engineering, 2009, 9(1): 62−66.

[11] 李国豪, 石洞. 公路桥梁荷载横向分布计算[M]. 2版.北京: 人民交通出版社, 1987. LI Guohao, SHI Dong. Calculation of lateral distribution of highway bridge load[M]. 2nd ed. Beijing: People’s Transport Press, 1987.

[12] 彭大文, 陈朝慰, 林志平, 等. 无伸缩缝桥梁荷载横向分布系数研究[J]. 公路交通科技, 2007, 24(9): 51−56. PENG Dawen, CHEN Zhaowei, LIN Zhiping, et al. Study on lateral load distribution coefficient of non-telescopic bridge[J]. Highway Traffic Technology, 2007, 24(9): 51− 56.

[13] 李秀芳, 吴锐福. 无伸缩缝桥梁荷载横向分布系数的有限元分析[J]. 公路交通科技, 2013, 30(12): 86−92. LI Xiufang, WU Ruifu. FEA of transverse load distribution factors for joint less bridge[J]. Journal of Highway and Transportation Research and Development, 2013, 30(12): 86−92.

[14] 钱寅泉, 周正茂, 王素娟, 等. 装配式小箱梁桥荷载横向分布数值分析与试验[J]. 公路交通科技, 2012, 29(1): 86−90. QIAN Yingquan, ZHOU Zhengmao, WANG Sujuan, et al. Numerical and experiment of lateral load distribution of fabricated small box girder bridge[J]. Journal of Highway and Transportation Research and Development, 2012, 29(1): 86−90.

[15] 聂瑞锋, 石雪飞, 阮欣, 等．在役多车道空心板梁桥弯矩横向分布系数计算方法研究[J]. 桥梁建设, 2014, 44 (2): 56−60.NIE Ruifeng, SHI Xuefei, RUAN Xin, et al. Research of calculation method for moment lateral distribution factors of multi-lane hollow slab beam bridges in service[J]. Bridge Construction, 2014, 44(2): 56−60.

[16] 邬晓光, 钱若霖, 苏佩. 考虑刚度损伤的装配式T梁桥横向分布计算[J]. 公路交通科技, 2018, 35(6): 61−66. WU Xiaoguang, QIAN Ruolin, SU Pei. Calculation of lateral distribution of prefabricated T beam bridge considering stiffness damage[J]. Highway Traffic Technology, 2008, 35(6): 61−66.

[17] 项贻强, 何余良, 刘丽思, 等．考虑滑移的多梁式组合小箱梁桥荷载横向分布[J]. 哈尔滨工业大学学报, 2012, 44(8): 113−118.XIANG Yiqiang, HE Yuliang, LIU Lisi, et al. Lateral load distribution of multi-box steel-concrete composite girder bridges for considering slipping effect[J]. Journal of Harbin Institute of Technology, 2012, 44(8): 113−118.

[18] 韦立林, 王文宁, 王建军. 简支梁桥荷载试验横向分布系数分析方法[J]. 广西大学学报(自然科学版), 2007, 32(2): 183−185, 199. WEI Lilin, WANG Wenning, WANG Jianjun. Analysis method of lateral distribution coefficient of load test of simply supported beam bridge[J]. Journal of Guangxi University (Nature Science Edition), 2007, 32(2): 183− 185, 199.

Calculation of transverse load distribution coefficient of assembled girder bridge considering main girder damage

LI Yuanjun, WU Xiaoguang, HUANG Cheng, XIAO Kailong, YING Yue

(School of Highway, Chang’an University, Xi’an 710064, China)

In order to calculate the transverse load distribution coefficients of assembled girder bridges under the condition of main girder damage, based on the load test data of 12 assembled T-girder and small box girder bridges, the measured values of the transverse load distribution coefficients were obtained. Considering the three key factors of vertical fundamental frequency, linear stiffness and width-span ratio, one was introduced. The damage reduction coefficient of main girder was fitted by the multivariate nonlinear regression analysis method of matlab software, and a calculation method of load transverse distribution coefficient considering the mechanical performance of the bridge is obtained. The calculation results were compared with the actual bridge data, finite element method (ANSYS) and traditional calculation methods. The results show that the calculation results of load transverse distribution coefficients of assembled girder bridges considering main girder damage are close to the actual bridge data.

bridge engineering; fabricated beam bridge; transverse load distribution coefficient; nonlinear regression analysis

U448.21

A

1672 − 7029(2019)06− 1459 − 07

10.19713/j.cnki.43−1423/u.2019.06.015

2018−07−22

贵州省交通运输厅科技资助项目(2015-121-024-1)；山西省交通运输厅科技资助项目(2017-1-37)；2016年度湖南省大学生研究性学习和创新性实验计划项目(697)

邬晓光(1961−)，男，湖北英山人，教授，博士，从事桥梁设计理论与桥梁检测加固研究；E−mail：wxgwst.cn@126.com

(编辑 阳丽霞)