沉积河谷对平面P波的二维散射

赵瑞斌，徐亚敏

（天津城建大学 a.土木工程学院；b.天津市软土特性与工程环境重点实验室，天津 300384）

国内外众多震害资料均显示，沉积河谷对地震动的扰动效应显著[1-2].如汶川大地震，国道G213 左侧某河谷场地在地震中出现附近山体滑坡现象[3]；在唐山地震、四川庐山地震等涉及沉积河谷的工程震害均造成非常严重的后果.河谷扰动效应主要源于两方面：一方面为土体介质自身松软特性；另一方面为河谷边缘对土体的盆地中心处形成聚焦效应，使得面波在其边缘转换，并与河谷下部的体波发生干涉作用，在浅层和地表形成地震波的放大效应.

沉积河谷对地震波的散射作用可采用两种方法求解，解析波函数展开法[4-6]和数值法.河谷数值模拟放大效应方面，已有的文献分别采用有限单元[7-11]、离散波函数法[12]、边界单元离散法[13-20]和混合法[21-22]研究了沉积盆地对地震波的地震响应.上述文献给出平面SH 波在河谷体系的出平面散射情况，而笔者则侧重于进一步研究河谷整体模型在P 波入射下的平面内地震响应.对比SH 波的散射情况，鉴于存在不同体波耦合面波的效应，计算和规律将复杂化.基于MATLAB 编程计算，采用边界间接积分方程法（indirect boundary integral equation method，简称 IBIEM），讨论频率、入射角和土层深度等对平面P 波在河谷体系的散射规律.

1 沉积河谷地震动分析模型

沉积河谷地震反应计算模型如图1 所示，其中半圆形沉积河谷存在于半空间.为简化计算，将模型分为半空间域、沉积域，各域假设为各向同性的均匀介质，定义半空间域和沉积域分别为DⅠ和DⅡ，沉积域与半空间域的交界面为T1.

图1 沉积河谷地震反应计算模型

各组成散射场构造如图2 所示.图2a 中，半空间散射波场在沉积边界作用下的虚拟波源记作S1；图2b中，沉积区散射波场在沉积边界作用下的虚拟波源记作S2，取S1、S2虚拟波源面的形状一致于河谷边界形状.

图2 各区域散射场构造

2 计算方法

2.1 自由场

依据Wong 等[23]的理论推导和文献成果，设在xoy坐标系下，半空间固体介质密度ρ，拉梅常数λ 和μ，P波入射角和反射角均为α，SV 波反射角为β.忽略时间因子后，入射P 波、反射P 波和反射SV 波的波势函数可分别表达为

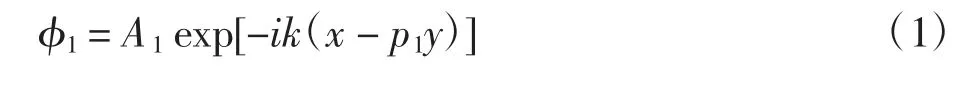
式中：φ1、φ2分别为 P 波入射与反射时的势函数；Ψ1为SV 波反射时的势函数；Vα、Vβ分别为半空间固体介质中的纵波和横波速度；Vx为波沿自由表面传播的水平向视速度.

反射 P、SV 波系数 A2、B1与入射 P 波系数 A1之比为

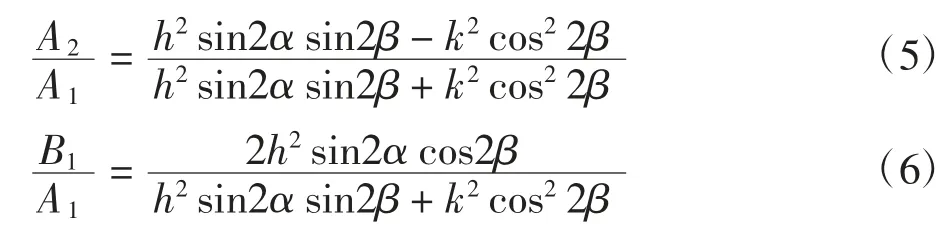
解得水平向和竖向位移函数ux和uy表达式为

式中：ω 为入射波的频率.

应力由几何方程和物理方程推得.

2.2 散射场

半空间DⅠ区散射位移波函数和应力波函数为

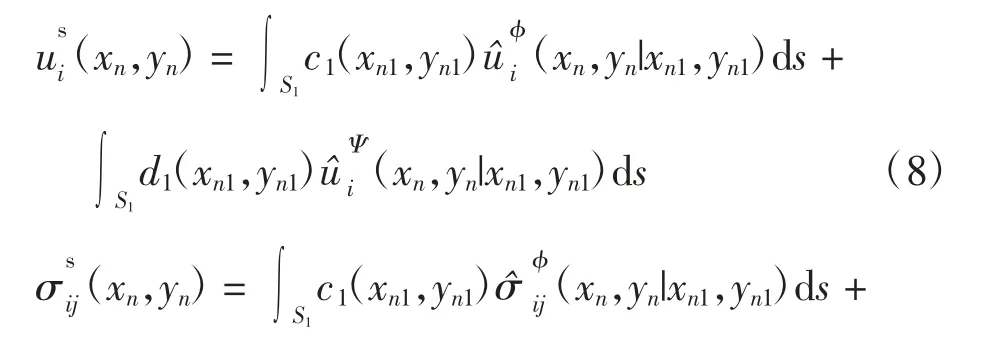
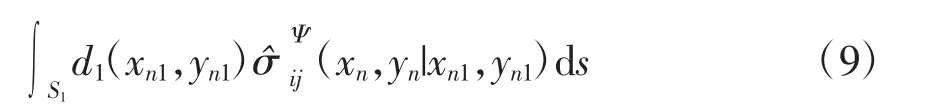
由式（8）和式（9）的积分形式转化，得

沉积DⅡ区散射位移波函数和应力波函数为

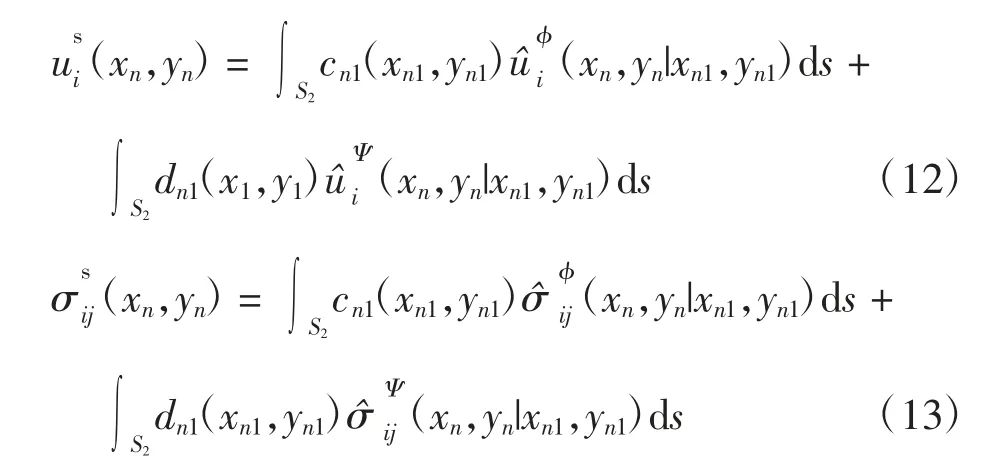
由式（12）和式（13）的积分形式转化，得

2.3 边界条件与求解

对于半空间中的P 波，构造半空间域动力格林函数符合地表应力为零条件；考虑交界面处位移、应力连续性，得

交界面T1位移u 连续性条件

交界面T1应力σ 连续性条件

边界T1及波源面S1和S2做如图2 所示的离散处理，将沉积域边界T1离散为均匀的N1 个观测点.交界面T1附近均布的S1、S2两圈波源点分别离散为M1和M2 个对沉积域与半空间域散射的波源点.由此可建立关于虚拟荷载密度的大矩阵方程

式中：G1为对沉积界面离散点作用的S1上所有波源点的应力格林函数矩阵；G2为对沉积界面离散点作用的S2上所有波源点的应力格林函数矩阵；T1为对沉积界面离散点作用的S1上所有波源点的位移格林函数矩阵；T2为对沉积界面离散点作用的S2上所有波源点的位移格林函数矩阵；FG为自由场应力；FT为自由场位移，Yi为波源密度.

解该矩阵可得虚拟波源密度.叠加自由场和散射场可得半空间反应的总位移u、总应力σ

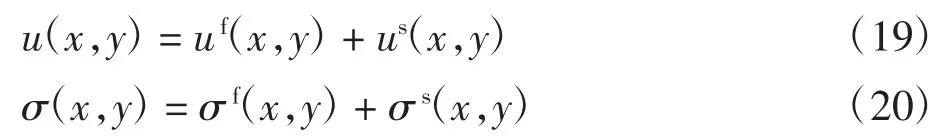
式中：uf、σf分别为平面P 波在自由场中的位移与应力；us、σs分别为平面P 波在散射场中的位移与应力.沉积河谷域仅需求得散射场.

3 精度检验

无量纲频率被定义为 η=2R/λ =ωR/πβ.经过大量参数计算表明：边界残值和边界离散点数成反比，对于低频η=0.5 及高频η=2.0，残差值均在10-5数量级以下，说明该方法具有很好的计算精度.

图3 为P 波作用情况下的地表位移幅值.本文程序参数设定：a = 30 m，E/a 为地表水平位移幅值，F/a为地表竖向位移幅值.黏滞阻尼比ζ=0.002，无量纲频率η = 0.5，河谷与半空间的剪切模量比为μ1∶μ2=4 ∶1，河谷半径 R/a=1.0（R=30 m）.选取 P 波垂直入射的情况，由图3 可知，本文模型的数值结果与文献[21]所得地表位移曲线幅值一致，从而验证本文方法的正确性.

图3 本文模型退化后地表位移与相关文献对比曲线

4 数值结果与分析

基于边界元间接积分方程法对比了大量的参数计算结果，着重讨论不同深度、入射角、频率作用时水平和竖向的土体内部位移因子的变化规律.波在两种介质（半空间，沉积区）中的剪切模量及传播速度比分别为 μ1∶μ2=4 ∶1，β1∶β2=2 ∶1.

4.1 多角度入射和不同频率下沉积域位移云图

为研究河谷在半空间的反应规律，图4-5 分别给出单一沉积场地内部水平和竖向位移云图.计算参数：a =30 m，E/a 为地下半空间沉积域内部土体水平位移幅值，F/a 为地下半空间沉积域内部土体竖向位移幅值.沉积域河谷半径R/a=1（R=30 m），入射角度分别为 0°、60°，无量纲频率 η 分别为 0.5、1.0、2.0.如图5 所呈现，沉积区域内部的位移特征由频率、入射角度等影响因子决定.垂直入射情况（即0°入射），低频时，位移峰值大多数聚焦于地表附近，峰值分布关于y 轴对称，且图形布局简单；高频时，沉积域对位移的扰动效应鉴于空间震荡的加剧变得更为复杂；地表和沉积内部同时出现数个地震波聚焦影响区域，这些峰值区域对地下结构造成一定的潜在安全影响.斜入射情况（即60°入射），位移峰值所在集中区域发生移动，且水平向位移放大幅值显著，可达到7.0.

4.2 不同观测点位和不同土层深度下位移频谱

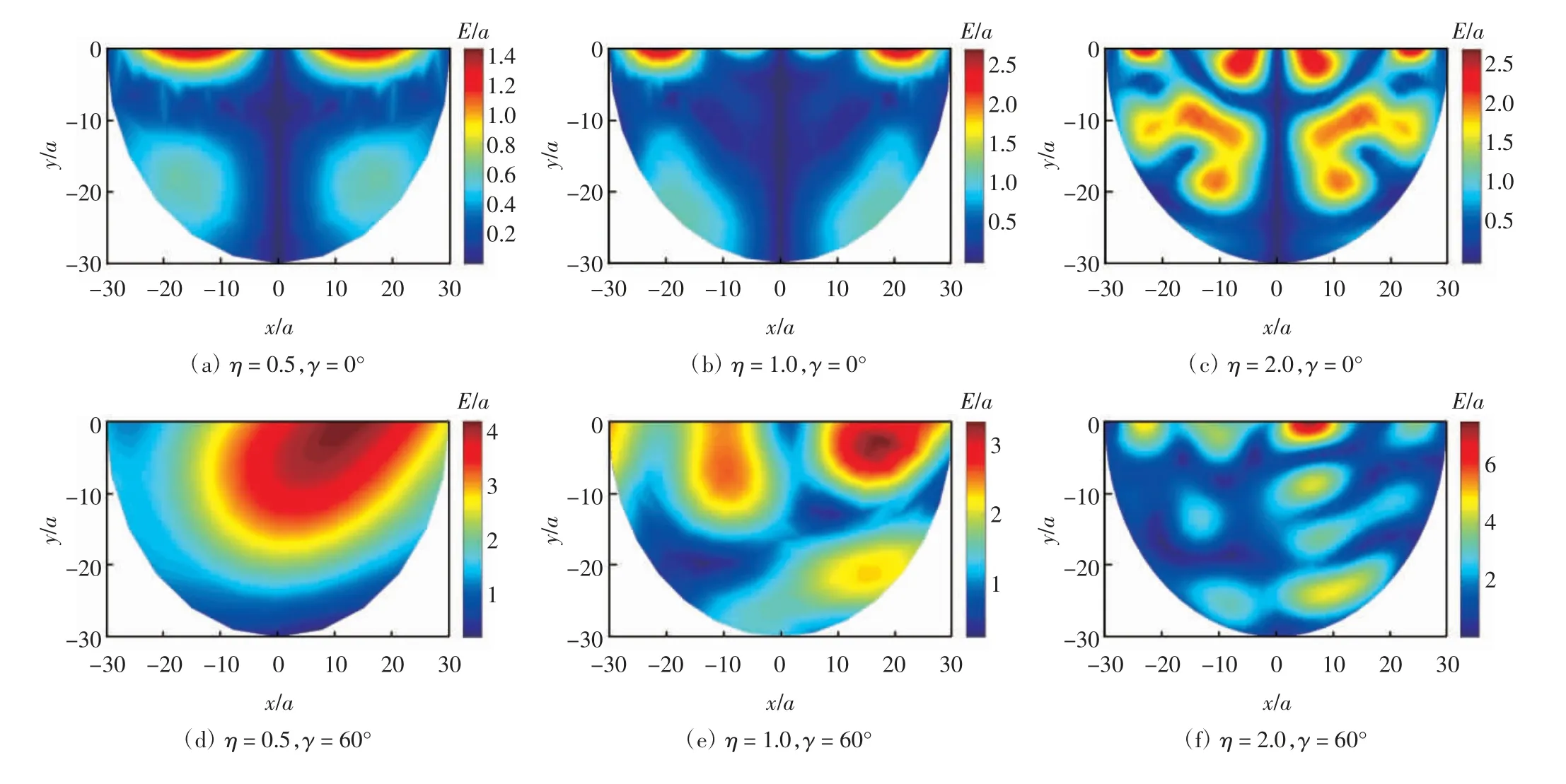
图4 多角度入射和不同频率下沉积域内水平位移幅值云图

图5 多角度入射和不同频率下沉积域内竖向位移幅值云图

图6 为单一沉积河谷给出的不同深度土层的位移频谱.参数设置：a=30 m，F/a 为地下半空间沉积土体竖向位移幅值.沉积河谷半径为R/a=1（R=30 m），无量纲频率η 取值范围0～10，土层深度分别为d/a =0.5、0.6、0.7（d=15，18，21 m），选取 6 个有代表性的观测点 x/a=0、0.2、0.4、0.6、0.8、1.0（x=0，6，12，18，21，27 m），地震波垂直入射.

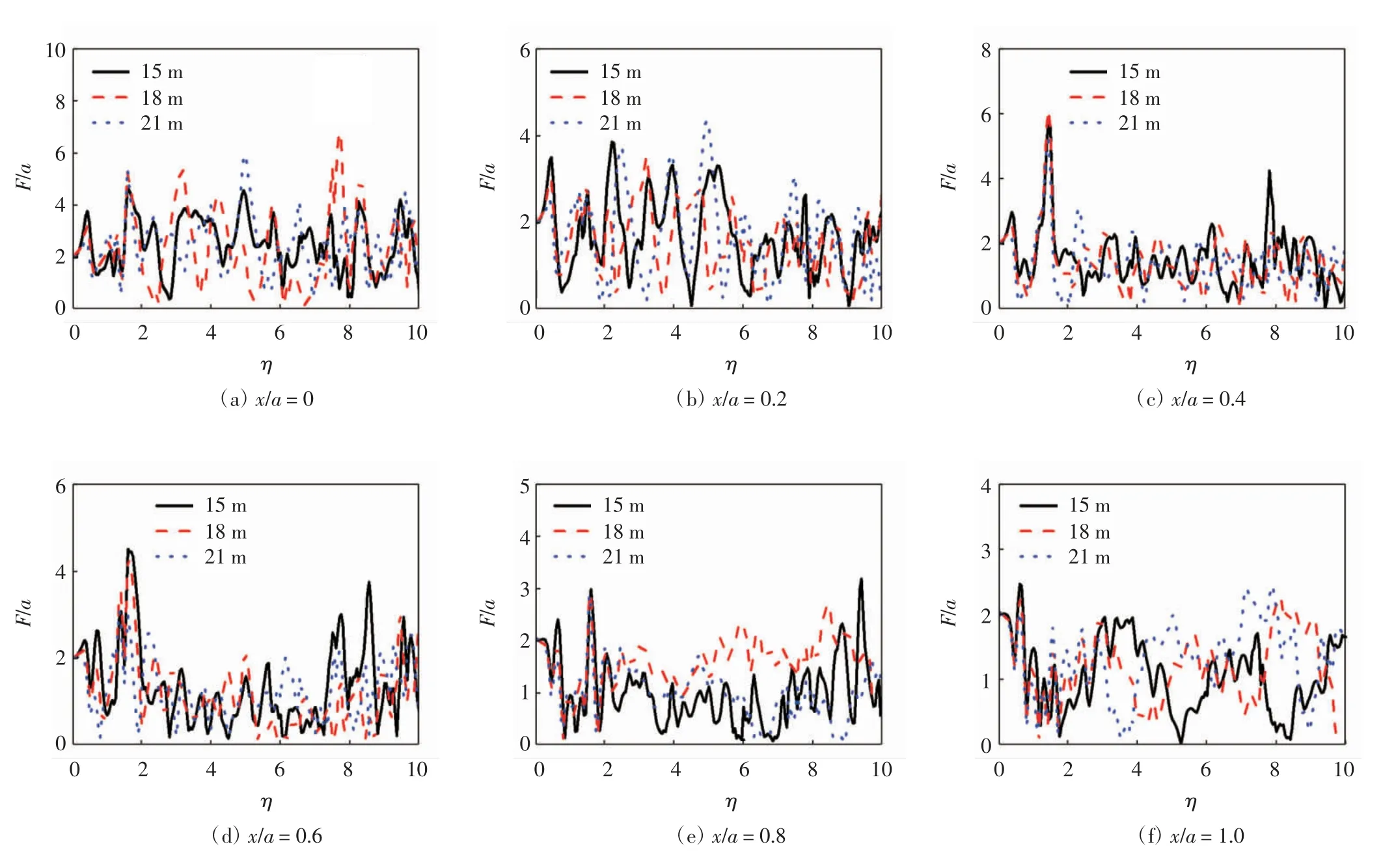
图6 沉积域内不同深度土层位移频谱图

由图6 可知：不同深度土层介质在0～2 的无量纲频率范围内，其位移频谱曲线特征值变化趋势与峰值大小较接近；而在2～10 无量纲频率范围内有明显差异，究其根本在于受沉积域不同深度自身固有频率的影响.沉积域同一深度的土体位移幅值随坐标点远离中心区域而变小，原因在于地震波垂直入射，经土层介质散射削弱了地震波的能量传播，所以在中心处取得最大峰值，在x/a=0.4（x=12 m）的位置处有突变在于此区域的土层介质频率与地震波频率接近，产生共振后的能量聚集效应.例如，土层深度为d/a=0.6（d =18 m）时，x/a=0.4（x=12 m）的位置附近，位移峰值于无量纲频率为1.5 时达到6，高出同参数下无量纲频率为0.5、6 时的位移幅值55%、60%.

4.3 Tar-Tarzana波入射沉积河谷内部土层加速度响应

时域结果的求解过程为：在频域无量纲频率0.05～10 内取200 个插值点，基于边界元-间接积分耦合法，输入Tar-Tarzana 波，频域位移经傅里叶变换得时域不同深度土层主方向位移时程和加速度时程.美国北岭地震Tar-Tarzana 波的位移时程曲线的卓越周期是0.336 s，时间间隔0.02 s，峰值加速度1 744 mm/s2.

图7 为Tar-Tarzana 波型P 波垂直入射时，沉积河谷内部不同深度土层典型观测点的加速度时程，土体深度分别为d=15，18，21 m.

从图7 整体上观察，加速度时程峰值与土层深度成正比.例如，典型代表点x/a=0（x=0 m）位置处，土层深度为 d/a=0.5、0.6、0.7（d=15，18，21 m）的最大峰值分别为1.9、2.0、2.1，分析其原因应为地震波在沉积区的散射随土层深度的加大而复杂化.

图7 沉积河谷内部不同土层深度加速度时程曲线

4.4 Tar-Tarzana波入射沉积河谷内部土层位移响应

图8 为Tar-Tarzana 波型P 波垂直入射时，沉积河谷内部不同深度土层典型观测点的位移时程，a=30 m，土体深度分别为 d/a= 0.5、0.6、0.7（d = 15，18，21 m），F/a 为地下半空间沉积土体竖向位移幅值.

由图8 可知：不同深度的位移时程曲线的变化趋势和峰值特征无明显差异，说明深度对土体位移时程影响不大.距离中心点的远近则导致峰值大小差距较大，且峰值大小与距中心点的距离成反比.例如：时间为2.5 s 时，土层深度d/a = 0.5（d = 15 m）处观测点x/a =0（x=0 m）的土体介质位移幅值是6，而同参数下观测点 x/a=0.2、0.4、0.6、0.8、1.0（x=6，12，18，21，27 m）处的位移幅值分别为 4、3、2.5、2.2、2.1.对比图 8 表明，沉积河谷中心点处位移震荡最剧烈，远离中心点则趋于平缓，因此实际地下工程应尽可能规避软土沉积河谷中心地带，或者采取有针对性的抗震加固措施.

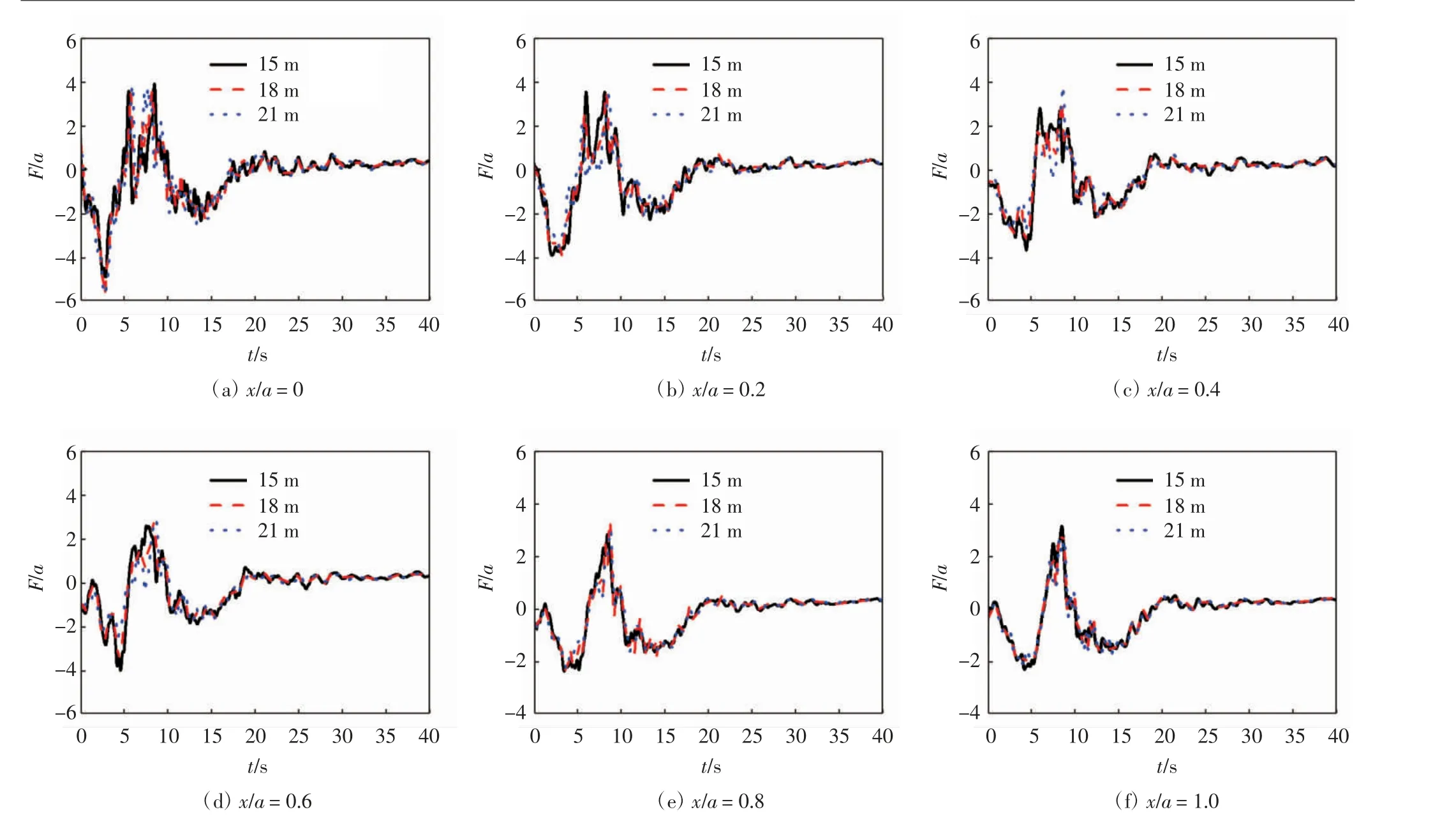
图8 沉积河谷内部不同土层深度位移时程曲线

5 结 论

从地震工程学角度，采用弹性波的边界间接积分方程法，分析了平面P 波对沉积河谷体系的散射规律，着重论述了沉积河谷土体的位移与频率、角度、深度的规律，结论如下.

（1）在0～2 无量纲频率范围内，沉积域不同深度土层介质位移随频率的变化趋势较一致；在2～10 无量纲频率范围内，位移变化趋势有较大的差异.

（2）中心观测点x/a=0（x=0 m）处位移时程取得最大峰值，远离中心点的最大峰值逐渐减弱.因此地下结构穿越沉积谷地时，须考虑河谷内部和边界的地震动的聚焦区域，以及复杂峰值分布特征，进而可优化地下结构线路规划，并适当加强地下结构的抗震设防等级.

（3）随土体深度的增加，加速度峰值振荡加剧，但增幅较小，说明浅层土体的深度变化对加速度时程影响较小.