五圆弧平底蛋形断面隧洞临界水深的简易算法

许晓阳，张根广，王愉乐

（西北农林科技大学水利与建筑工程学院，陕西杨凌712100）

五圆弧平底蛋形断面是文献［1］中规定的5种水工隧洞专用断面之一，与四圆弧断面、六圆弧断面相比，五圆弧平底蛋形断面将底拱改为了平底，因此该形断面不仅具有蛋形断面的优点，即受力条件好、水力性能优越，而且具有断面结构简单和施工尺寸容易控制等优点，是广泛采用的断面形式之一。

临界水深是输水隧洞设计及水力计算中控制水流形态变化的重要参数，其传统计算方法有试算法、迭代法和查图法等，计算过程繁琐，一般无法直接给出解析解。因此，为了给工程应用提供简单的计算公式，研究五圆弧平底蛋形断面的临界水深计算公式就显得非常必要。目前，国内外学者的研究多集中在四圆弧、六圆弧和马蹄形等断面的水力计算。张志昌等［2］根据明渠均匀流基本理论、明渠恒定非均匀流基本理论和平底明渠水跃的基本方程，提出了标准Ⅰ型四圆弧蛋形断面正常水深、临界水深、水跃共轭水深、水面曲线的计算方法；卞晓卫等［3］利用1stOpt软件，基于遗传算法，对给定的非线性函数模型进行了参数优化拟合，建立了蛋形断面正常水深和临界水深的显性计算公式；文辉等［4］应用拟合法提出了蛋形断面管道临界水深近似计算公式；滕凯［5］依据优化拟合理论，以标准剩余差最小为目标函数，通过对4个分段函数的逼近拟合，获得了六圆弧蛋形断面临界水深通用计算公式；李若冰等［6］根据明渠恒定非均匀流理论，按照分块计算面积的方法，详细推导了六圆弧蛋形断面临界水深和收缩断面水深的迭代计算公式，并根据优化拟合研究了临界水深的简化计算方法；文辉等［7］通过对平底Ⅰ型马蹄形断面临界流方程进行数学变换，应用拟合原理得到了平底Ⅰ型马蹄形断面临界水深的近似计算公式；滕凯［8］依据优化拟合理论，以标准剩余差最小为目标函数，在工程适用参数范围内拟合得到了一个形式简单、便于应用的通用简化公式；武周虎［9］在分段曲线拟合和优化分析的基础上，分别给出了德式蛋形断面以正常水深模数和以临界水深模数为自变量的充满度直接计算公式；张志昌等［10］根据面积分割法计算了六圆弧蛋形断面的面积、湿周和水力半径，根据明渠均匀流理论计算了不同流量时渠道的正常水深，通过优化拟合研究了蛋形断面正常水深的简单计算方法。但是，对于五圆弧平底蛋形断面形式的临界水深计算尚未见到研究成果，为此，本文计算了五圆弧平底蛋形断面的水力要素方程，得到了3种典型断面的过水断面面积和水面宽度，并对临界水深的基本计算公式进行数学变换，对无量纲临界水深和无量纲参数的关系进行研究分析，利用优化拟合理论，在工程适用范围内推导了3种典型五圆弧平底蛋形断面临界水深的简易计算公式。

1 五圆弧平底蛋形断面临界水深的基本计算公式

根据水力学［11］定义，当明渠的流量、断面形状保持不变时，相应于断面比能最小值的水深称为临界水深。据此可以得到平底明渠临界水深的基本计算公式为

式中：α为流速分布不均匀系数，通常取1.0；Q为设计流量，m3/s；g 为重力加速度，取 9.8 m/s2；Ak为临界水深时过水断面面积，m2；Bk为临界水深时过水断面的水面宽度，m。

1.1 五圆弧平底蛋形断面形状特征参数

五圆弧平底蛋形断面形状见图1，是由5段圆弧和底部直线段组成的封闭断面，即由半径分别为r1、r2和r3的5段圆弧和长度为b-2r1的直线段组成，最大宽度为b，最大洞高为H。圆弧段对应圆心角如图1所示，底部水平直线段两端的圆弧段圆心角为0.5π，中部扇形区域圆心角为θ，顶拱段圆弧对应的圆心角为π-2θ。

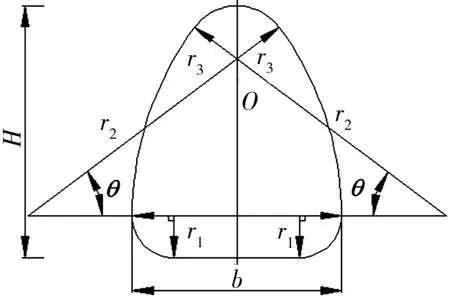
图1 五圆弧平底蛋形断面形状参数

1.2 五圆弧平底蛋形断面水力要素计算公式

五圆弧平底蛋形断面水力要素计算参数如图2所示，其中α、β、γ分别为水深位于底部圆弧区域、中部圆弧区域和拱顶区域时的辅助角度参数。根据五圆弧平底蛋形断面形状特征，若取无量纲水深为x（x＝h/b，h为洞内水深），则不同水深处的过水断面面积A和水面宽度B等水力要素可用分段函数表示。

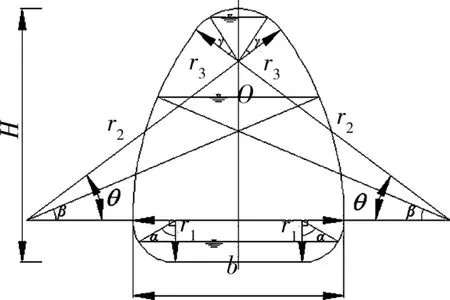
图2 五圆弧平底蛋形断面水力要素计算参数

当水深位于底部圆弧形区域时（即0＜h≤r1），A、B的计算公式分别为

当水深位于中部圆弧区域时（即 r1＜h≤r2sin θ+r1），A、B 的计算公式分别为

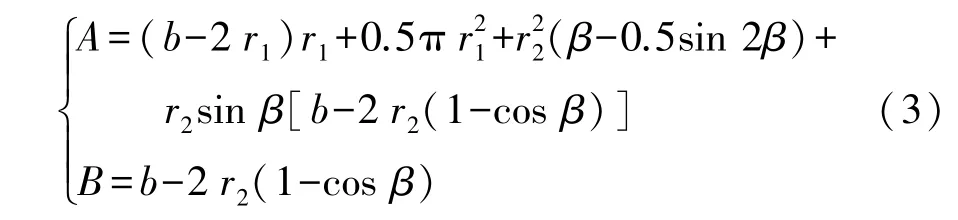
当水深位于顶拱区域时（即r2sin θ+r1≤h），A、B的计算公式分别为

1.3 五圆弧平底蛋形典型断面水力要素计算

水工设计手册［1］给出了常用的无压隧洞五圆弧平底蛋形典型断面的形状特征参数，断面类型可分为Ⅰ型断面、Ⅱ型断面和Ⅲ型断面，特征参数见表1。

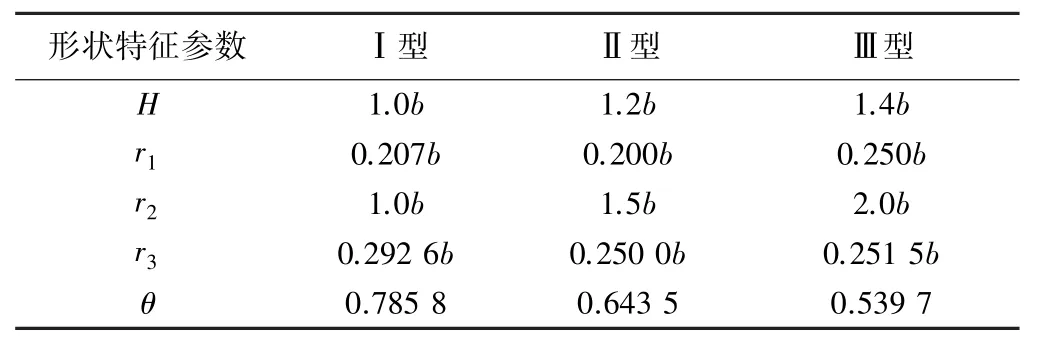
表1 五圆弧平底蛋形典型断面的形状特征参数

将表1中3种典型断面的形状特征参数代入式（2）～式（4），即可得到3种五圆弧平底蛋形典型断面的水力参数，结果见表2。

表2 五圆弧平底蛋形典型断面水力参数

1.4 临界水深的基本计算公式

将表2中3种五圆弧平底蛋形典型断面的水力要素分别代入式（1），经过简单的数学变换，同时设无量纲综合参数k为

经简单整理即可得到五圆弧平底蛋形断面临界水深的基本计算公式，本文仅给出Ⅰ型断面临界水深的基本计算公式，Ⅱ型、Ⅲ型断面的基本计算公式结构和Ⅰ型的类似。Ⅰ型断面无量纲临界水深在0≤x＜0.207、0.207≤x＜0.914、0.914≤x＜1 时的基本计算公式分别为

在实际工程应用中，可以直接由Q和b求取k值，由式（6）可知，若已知k值，则可以由式（6）通过迭代或者试算求解无量纲临界水深x，并通过下式计算断面临界水深hk为

对于Ⅰ型断面的无量纲临界水深基本计算公式，就数学意义而言，x理论取值范围为0～1，但在实际工程中，在较小过流情况下实际意义不大。文献［8］认为当水深小于整个隧洞洞高的0.05倍时可认为是较小过流情况，对于Ⅰ型、Ⅱ型、Ⅲ型断面，当xⅠ≤0.05、xⅡ≤0.06、xⅢ≤0.07时，即可认为属于较小过流情况。此外，《水工隧洞设计规范》（SL 279—2016）［12］中规定，隧洞中水面线以上空间面积不小于整个隧洞断面面积的15%，或者水面线以上净高不低于0.4 m。据此经过试算，可以求得当 xⅠ≤0.745 8、xⅡ≤0.889 8、xⅢ≤1.048 2时符合规定，此时相应的无量纲综合参数kⅠ∈［0.040 6，0.763 2］、kⅡ∈［0.049 8，0.913 7］、kⅢ∈［0.054 7，1.069 2］。

2 临界水深的近似公式及精度分析

2.1 临界水深拟合公式的建立

根据前文所述计算公式，由无量纲综合参数k来求解临界水深计算较为繁琐，无法直接给出解析解，因此需要得到临界水深的简易算法。以Ⅰ型断面为例，在x的取值范围内以一定的步长值给定一组数值，将其代入式（6），即可求得相应的k值。运用Matlab软件采用最小二乘法求解目标函数，对散点（k，x）进行拟合分析，在拟合过程中根据散点图的曲线形状选取合适的用户模型，使得拟合公式的相关系数最大，即可得到无量纲临界水深的直接计算公式。

对于Ⅰ型断面，有

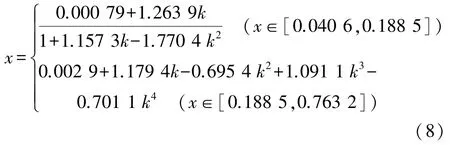
Ⅱ型断面无量纲临界水深计算公式为

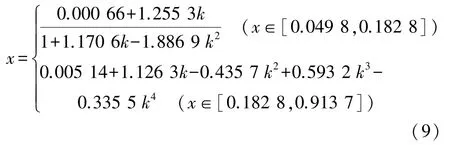
Ⅲ型断面无量纲临界水深计算公式为

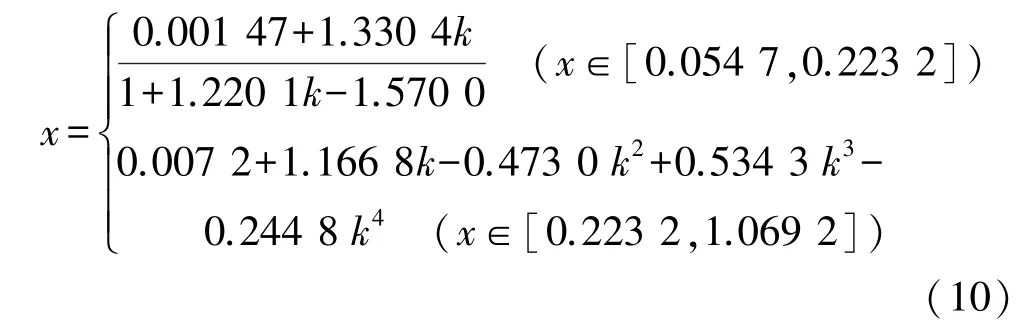
若已知k值，则可以由式（8）～式（10）分别计算Ⅰ型断面、Ⅱ型断面和Ⅲ型断面无量纲临界水深x的数值解，并通过式（7）计算各断面临界水深。

2.2 临界水深拟合公式精度分析

以Ⅰ型断面为例分析拟合公式的精度。在已经确定的无量纲临界水深范围内给出xi的值，并将xi的值代入式（6）求ki的值，再将ki值代入式（8）求取无量纲临界水深的近似值x′i，采用相对误差比较给定的真值xi与求出的近似值 x′i（由式（11）计算），其相对误差分布情况见图3（a）。同理，可得出Ⅱ型断面和Ⅲ型断面拟合公式的误差分布情况。

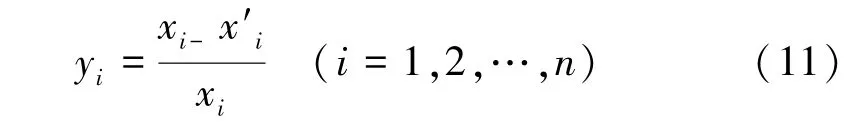
式中：yi为拟合的相对误差；xi为真值；i为拟合公式精度分析的第i个数据。

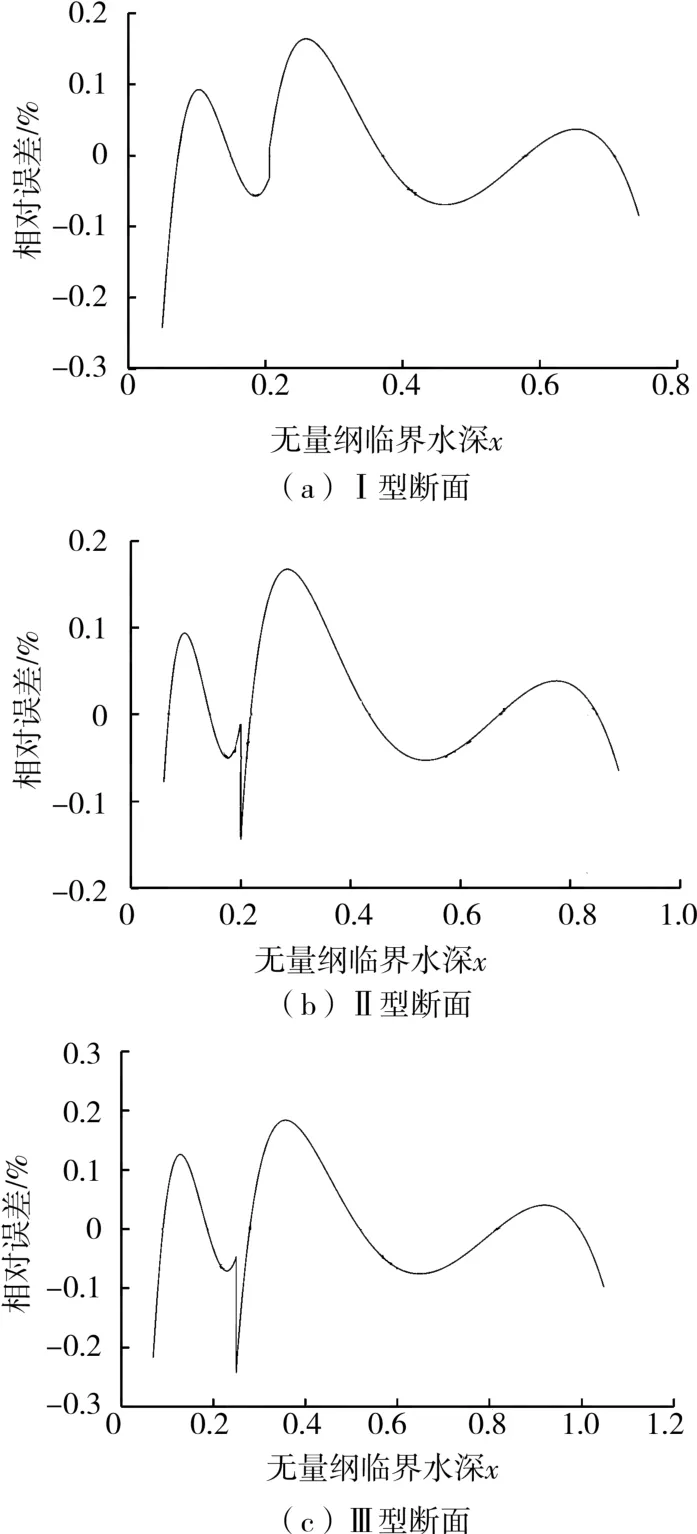
图3 五圆弧平底蛋形典型断面临界水深相对误差分析

由图3可知，当无量纲临界水深x取值在工程适用范围内时，三种断面最大相对误差的绝对值小于0.24%，大部分区域相对误差在0.1%内正负波动，相对误差的最大值多出现在无量纲临界水深x取值范围的端点处；在公式对应的x取值范围内，随着无量纲临界水深x的增大，相对误差的绝对值逐渐减小。由误差分析可见，本文拟合得到的无量纲临界水深直接计算公式可满足工程需要，是3种五圆弧平底蛋形典型断面临界水深的简易且高精度的计算方法。

3 应用举例

某五圆弧平底蛋形断面引水隧洞，断面最大宽度b＝8.6 m，设计流量为320 m3/s，校核流量为430 m3/s，利用本文拟合公式分别计算当采用Ⅰ、Ⅱ、Ⅲ型断面时的隧洞临界水深hk。具体计算步骤：①计算k值，由k＝可得 k＝ 0.605 6，k＝ 0.737 5；②将 k值设计校核代入式（8）～式（10）相对应的分段函数方程中，计算出无量纲临界水深x值；③根据x＝h/b，可得到对应的临界水深hk值。

经计算得，采用Ⅰ型断面时，临界水深的数值解分别为5.247 2、6.233 0，经过Excel计算的临界水深精确值分别为5.246 0、6.235 0 m，相对误差绝对值分别为0.022 6%、0.032 1%；采用Ⅱ型断面时，临界水深的数值解分别为5.281 3、6.342 5 m，经过Excel计算的临界水深精确值分别为5.283 0、6.340 8 m，相对误差绝对值分别为0.031 1%、0.032 3%；采用Ⅲ型断面时，临界水深的数值解分别为5.383 6、6.470 6 m，Excel计算的临界水深精确值分别为5.357 9、6.473 2 m，相对误差绝对值分别为0.073 9%、0.040 1%。由此可见，拟合公式精度很高，完全满足工程需要。

4 结 论

五圆弧平底蛋形断面临界水深计算公式复杂，为分段的超越方程，求解过程繁琐，且无法直接给出解析解。本文通过优化拟合，在工程适用范围内推导了3种典型五圆弧平底蛋形断面临界水深的简易计算公式，并对公式进行了精度分析，结果表明拟合公式的最大相对误差绝对值小于0.24%，大部分区域相对误差在0.1%内正负波动，完全满足实际工程的精度需要，同时，本文推导的公式结构简单、便于运算，即使使用简单的计算器也可进行正确、高效的计算，实用性很强。