Adam优化的CNN超分辨率重建*

赵小强，宋昭漾

1.兰州理工大学 电气工程与信息工程学院，兰州 730050

2.甘肃省工业过程先进控制重点实验室，兰州 730050

3.兰州理工大学 国家级电气与控制工程实验教学中心，兰州 730050

1 引言

在生活的许多场景中，人们用成像设备获得的图像在某些细节方面表现得都不是特别好。为了更好地获得图像细节信息，图像超分辨率重建（superresolution，SR）技术引起研究者的广泛关注。它是一种通过使用计算机将一幅低分辨率图像（low resolution，LR）或图像序列进行恢复得到高分辨率图像（high resolution，HR）的图像处理技术。通过恢复得到的高分辨率图像具有更丰富的细节信息，这些细节信息在实际应用中会起到非常重要的作用。在1984年，超分辨率重建技术首次被Tsai等[1]提出。由于图像超分辨率重建技术在生活中应用非常广泛并且技术要求也越来越高，使得图像超分辨率重建技术得到快速发展。目前图像超分辨率重建技术主要分为3种方法：基于插值、基于重建和基于学习的方法[2]。

基于插值的方法有最近邻插值、双线性插值和双立方插值方法。最近邻插值方法是用最临近的点的像素值表示目的像素值，该方法的特点是插值速度快，但是缩放图像质量差，并且图像容易失真。双线性插值方法具有低通滤波器的特点，使用双线性插值方法得到的重建图像质量比较好而且图像较平滑，得到重建图像的速度也较快，但是使用双线性插值方法使图像的高频分量受损。使用双立方插值方法得到的图像质量较好，但是计算量很大，计算速度也比较慢。目前，双立方插值方法一般用于图像的预处理工作。虽然基于插值的方法在一定程度提高了图像细节信息的清晰度，但是存在较严重的震荡和过平滑问题。研究人员为了解决震荡和过平滑问题，提出了基于重建的方法。基于重建的方法是对图像建立观测模型，结合不同的先验条件进行高分辨率图像的求解。基于重建的方法包括凸集投影（projection onto convex sets，POCS）方法[3]和最大后验概率（maximum a posterior，MAP）方法[4]。凸集投影方法是一种采用迭代的方法，其方法思想比较简单，加入先验知识也比较容易，但是该方法计算过于复杂，收敛速度也比较慢。最大后验概率方法是将低分辨率图像序列的配准问题基于概率进行优化求解，估计出高分辨率图像。最大后验概率方法使用比较灵活，可以加入对具体问题的具体约束，但是使用最大后验概率方法容易造成图像平滑和重要细节的缺失问题。基于重建的方法需要充分的先验知识，随着放大因子的增大，即使增加低分辨率图像，也很难对图像高频信息进行重建，甚至会造成图像平滑问题。基于学习的方法是对图像进行特征提取、非线性映射和图像重建得到高分辨率图像。基于学习的方法包括流行学习、稀疏表示和深度学习方法。Chang等[5]将流行学习中的局部线性嵌入法应用到图像超分辨率重建中，减少了训练集的数量，但是容易产生欠拟合和过拟合问题。Yang等[6]将稀疏表示模型（sparse coding for super-resolution，SCSR）应用到图像超分辨率重建，这种方法虽然高效，但是忽略了整体框架优化，很难得到最优的参数。

近年来，深度学习[7-9]在图像处理领域中表现出巨大潜力，引起了研究者的广泛关注。Wang等[10]将稀疏编码与深度学习结合应用于图像重建；Dong等[11]提出了基于卷积神经网络的超分辨率重建（superresolution convolution neural network，SRCNN）方法；在SRCNN[11]算法中，将重建过程中的图像块提取、非线性映射和图像重建3个操作统一到一个3层的卷积神经网络中，实现了从低分辨率图像到高分辨率图像端到端的学习，使得图像重建性能得到了很大的提高。但是仅仅用3层网络学到的图像特征信息有限，没有充分利用图像区域之间信息的关联性，导致在不同放大倍数的条件下图像重建的效果差别很大。

为了解决单帧图像在不同放大倍数的条件下进行超分辨率重建能得到良好的效果，提出了一种Adam优化的卷积神经网络（CNN）超分辨率重建方法。该方法首先使用ISODATA聚类算法对训练的图像集进行分类处理，减少卷积神经网络参数的复杂度；然后在Adam优化的卷积神经网络中对输入图像进行特征提取和非线性映射得到特征映射图；最后在Adam优化的卷积神经网络中对特征映射图进行反卷积重建得到多尺度放大的重建图像。

2 卷积神经网络

卷积神经网络是人工神经网络的一种。1984年Fukushima首次提出的神经认知机就是最原始的卷积神经网络，Fukushima将其运用在手写数字识别上面。随着研究人员对卷积神经网络的深入研究和不断完善，卷积神经网络被成功应用在图像处理、模式识别等领域。卷积神经网络是一个具有多层的神经网络，主要包括数据输入层、卷积计算层、池化层和全连接层。数据输入层的作用是对原始数据进行预处理，包括去均值、归一化、PCA/白化操作等；卷积计算层对输入数据进行卷积操作，实现特征提取；池化层用于压缩数据、压缩参数数量和减小过拟合；全连接层对所有特征都进行不同权重连接，实现输出。卷积神经网络的每一层都包含多个二维平面，而每个二维平面都由多个独立的神经元组成。卷积神经网络的卷积计算层由多个特征映射平面组成，映射平面上所有神经元的权值相等，由于映射平面上的神经元共享权值，因此减少了网络参数的个数，降低了网络参数的复杂度。卷积神经网络的每一个卷积计算层通常后面连接池化层，这种结构对输入图像具有很好的畸变容忍能力，对平移、比例缩放、倾斜或者其他形式的形变具有高度不变性。图像重建的卷积神经网络模型如图1所示，最左边是卷积神经网络的输入层，然后卷积层对输入层的特征图进行卷积计算，接着对卷积层的特征图进行池化操作。卷积层和池化层的组合可以在隐藏层中出现很多次，在图1的模型中只出现两次。最后池化层的特征图通过全连接层实现重建，得到重建图像。

3 Adam优化的CNN超分辨率重建

3.1 采用ISODATA聚类算法对训练的图像集进行分类处理

在图像超分辨率重建过程中，采用传统的K-means聚类算法[12]对训练的图像集进行分类处理可以提升训练效果和减少训练时间。在K-means聚类算法中，k的值需要预先人为确定，在整个算法使用过程中k的值也无法更改，并且当训练高维度的数据集时，很难准确估计k值的大小。

本文采用ISODATA聚类算法代替K-means聚类算法，ISODATA聚类算法可以把某个样本数量过少的类别去除，把某个样本数量过多、分散程度较大的类别分为两个子类别。ISODATA聚类算法基本步骤如下：（1）选择初始聚类中心和参数指标，将N个样本按照指标分配到各个聚类中心；（2）计算各类样本的距离指标函数；（3）按照给定的要求，将前一次获得的聚类集进行分裂和合并处理，从而获得新的聚类中心；（4）重新进行迭代计算，计算各项指标，判断聚类结果是否符合要求。经过多次迭代后，若结果收敛，则运算结束。ISODATA聚类算法的流程图如图2所示，其中K表示预期聚类的数目，NC表示当前形成的聚类数目。

在卷积神经网络的训练中，使用ISODATA聚类算法对训练的图像集进行分类处理，将近似的图像分成一类，减少卷积神经网络模型的参数规模，从而能够在一定程度上减少卷积神经网络的训练时间，提高卷积神经网络的训练效率。

3.2 特征提取与非线性映射

本文采用将合适的低分辨率图像输入到卷积神经网络的方法进行特征提取和非线性映射。在卷积神经网络中每个神经元的作用就是相当于只关注图像某一个特征的滤波器，所有神经元组合在一起的作用就是相当于对整幅图像进行特征提取。卷积神经网络对图像特征提取是从输入的图像中提取图像块并把每一个图像块表示成高维向量，这些向量组成第一层的特征映射图[13]。设这一层的操作为F1，输入图像为Y，则该层操作运算表示为：

其中，W1为滤波器，W1的大小为c×f1×f1×n1，c为YCbCr色彩空间中图像的通道数，f1为滤波器的大小，n1为滤波器的数量，B1为偏差，“*”表示卷积操作，a服从均匀分布a～U(l,u)。这个卷积层的含义为运用大小为c×f1×f1×n1的滤波器W1作用在输入的低分辨率图像上，对输入的低分辨率图像进行特征提取，得到n1维特征映射图。

同样，非线性映射则是通过卷积神经网络将第一层的n1维向量映射到第二层的n2维向量中，得到n2维特征映射图。设这一层的操作为F2，输入图像为F1(Y)，则该层操作运算表示为：

其中，W2是大小为n1×f2×f2×n2的滤波器，B2是n2维的偏差。这个卷积层的含义为运用大小为n1×f2×f2×n2的滤波器W2作用在第一层的特征映射图上，进行非线性映射，得到n2维特征映射图。

3.3 反卷积重建

本文通过设计一个反卷积操作实现图像多尺度重建，该操作能够对获得的特征映射图进行多尺度放大[14]。反卷积[15]（deconvolution）又被称为转置卷积（transposed convolution），因为卷积层的前向传播过程就是反卷积层的反向传播过程，卷积层的反向传播过程就是反卷积层的前向传播过程。在图像反卷积操作过程中，当步长s大于1时，反卷积可以看作是上采样操作，并且整个网络的复杂度也会降低s2，但是步长也不能过大，因为步长过大图像的重建质量就会严重下降。在图像反卷积重建过程中，对于有重叠区域的图像块采用平均化操作得到最终图像。平均化操作可视为在特征映射图上采用均值滤波器。设这一层的操作为F3，输入图像为F2(Y)。本文设计的反卷积操作的表达形式为：

其中，W3是大小为n2×f3×f3×c的滤波器，B3是c维的偏差，“⊗”表示反卷积操作，σ为采样因子。步长根据采样因子的大小进行相应的调整，且步长始终大于1。

3.4 Adam优化CNN网络

对于CNN网络的参数，本文通过构建均方误差函数作为损失函数，最小化F(Y;θ)与原始图像X的误差来估计网络参数θ={W1,W2,W3,B1,B2,B3}。均方误差函数表达形式为：

其中，n代表训练图像的数量。

为了优化CNN网络，更新网络参数θ，本文采用Adam优化算法[16]代替随机梯度下降（stochastic gradient descent，SGD）算法来最小化损失函数。随机梯度下降算法保持单一的学习率（alpha）更新所有的权重，学习率在网络训练过程中并不会改变。而Adam优化算法通过计算梯度的一阶矩估计和二阶矩估计为不同的参数设计独立的自适应性学习率。Adam算法有很高的计算效率和较低的内存需求，并且Adam算法梯度的对角缩放（diagonal rescaling）具有不变性。更新网络参数过程表示为：

其中，gt是均方误差函数L(θ)对θ的梯度，mt是对梯度的一阶矩估计，nt是对梯度的二阶矩估计，m̂t是对mt的偏差修正，n̂t是对nt的偏差修正，矩估计的指数衰减速率u为0.9，v为0.99，步长η为0.001，数值稳定的小常数ε为10-8，Δθt是计算的θt更新值，θt+1为t+1时刻的θ值，即将θt和 Δθt的值求和应用到θt+1。Adam优化算法首先对参数向量、一阶矩向量和二阶矩向量进行初始化。然后循环迭代地更新各个部分，使参数θ收敛。即时间步t加1，更新偏差的一阶矩估计和二阶矩估计，接着计算一阶矩估计的偏差修正和二阶矩估计的偏差修正，再更新目标函数在该时间步上对参数θ所求的梯度，最后再用以上计算出来的值更新模型的参数θ。基于Adam优化的CNN超分辨率重建操作图如图3所示，首先对训练集进行ISODATA聚类，将人脸的图像分为一类，然后将分类后的训练图像输入到神经网络，训练神经网络参数，最后将重建的LR图像输入到训练好的神经网络进行特征提取、非线性映射和反卷积操作得到重建图像。

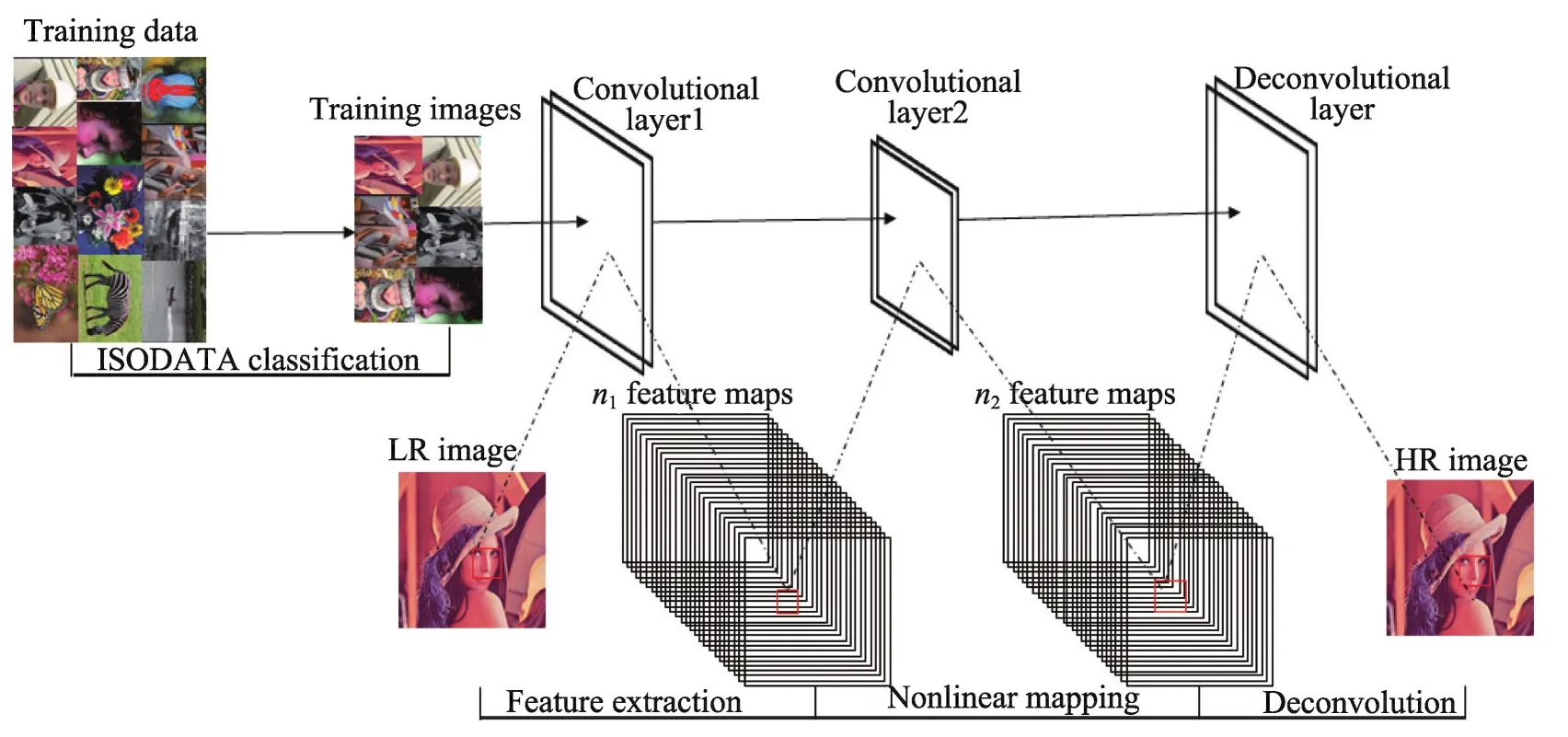
Fig.3 Operation diagram of CNN super resolution reconstruction based onAdam optimization图3 基于Adam优化的CNN超分辨率重建操作图

4 实验与分析

4.1 初始化

本文的实验在Intel®Pentium®CPU3550M平台上进行，主频为2.30 GHz，内存为4 GB，其中卷积神经网络在深度学习框架Caffe上搭建，实验测试在Matlab2014（a）中进行。

在实验中，训练卷积神经网络的图像集为常用的91幅自然图像，运用Set5和Set14测试集对卷积神经网络进行测试。

实验中的参数设置：f1=9,f2=1,f3=5,n1=64,n2=32,u=0.9,v=0.99,η=0.001,ε=10-8，一阶矩mt和二阶矩nt初始化设置为0，一阶矩的偏差修正m̂t和二阶矩的偏差修正n̂t初始化设置为0。

为了客观评估使用本文方法获得的重建图像的质量，使用经典的Bicubic算法、SRCNN算法和FSRCNN（fast super-resolution convolutional neural network）算法对相同的图像进行超分辨率重建并进行对比。经典的Bicubic算法是基于插值的超分辨率重建算法，一般用于图像超分辨率重建的预处理工作。SRCNN算法是基于深度学习的超分辨率重建算法，在图像应用中具有空间平移、旋转和缩放不变性，且通过权值共享大大减少了所需要训练的参数。FSRCNN算法是SRCNN的改进算法，FSRCNN算法使用了更小的卷积核缩减了参数计算量并加快了训练速度。

本文实验采用峰值信噪比（peak signal to noise ratio，PSNR）来评价各种算法的重建效果。

其中，MSE表示当前图像X和参考图像Y的均方误差（mean square error）；H和W分别为图像的高度和宽度；n为每像素的比特数，一般取8，即像素灰阶数为256；PSNR的单位是dB，数值越大表示失真越小。

4.2 实验效果

实验采用放大倍数2、3、4分别获得本文方法与Bicubic算法[17]、SRCNN算法[11]和FSRCNN算法[18]重建图像的PSNR值，如表1～表3所示。

Table 1 PSNRvalues of reconstructed images with magnification factor of two表1 放大倍数为2的重建图像的PSNR值 dB

Table 2 PSNRvalues of reconstructed images with magnification factor of three表2 放大倍数为3的重建图像的PSNR值 dB

Table 3 PSNRvalues of reconstructed images with magnification factor of four表3 放大倍数为4的重建图像的PSNR值 dB

从表1～表3中可以分析出，当放大倍数为2时，使用本文方法得到的重建图像质量差于使用Bicubic算法得到的重建图像质量，这是因为Bicubic算法是基于插值的方法，放大倍数越小，插值容易且对图像的影响较小。而SRCNN算法、FSRCNN算法和本文方法是基于学习的方法，图像上下文数据信息缺少关联。当放大倍数为3和4时，使用本文方法得到的重建图像质量优于使用另外3种算法得到的重建图像质量。在放大倍数为3的情况下，使用本文方法得到的重建图像质量最好，使用本文方法比使用Bicubic算法获得的重建图像的PSNR值平均提高了1.87 dB，比SRCNN算法得到的重建图像的PSNR值平均提高了0.04 dB，比FSRCNN算法得到的重建图像的PSNR值平均提高了0.013 dB。

在放大倍数为3的情况下，对Set5和Set14测试集使用本文方法和其他3种算法分别重建的图像结果如图4、图5所示。（a）图为使用双立方插值（bicubic interpolation）重建算法得到的图像，（b）图为使用基于CNN的超分辨率（SRCNN）重建算法得到的图像，（c）图为使用FSRCNN算法得到的图像，（d）图为使用本文方法得到的图像。在Set5中的蝴蝶重建图像对比图中进行观察，如图4所示，（d）图比（a）、（b）、（c）图重建效果更好，细节表现更丰富,蝴蝶翅膀上的花斑表现得很清晰。在Set14中的狒狒重建图像对比图中进行观察，如图5所示，（d）图比（a）、（b）、（c）图在纹理细节区域表现得更好，狒狒的毛发看起来更清晰，没有模糊感。在Set5、Set14测试集其他的图像中也可以得到同样的结果。因此，对同一幅图像进行超分辨率重建时，与Bicubic算法相比，使用本文方法得到的图像更清晰，细节表现得更丰富；与FSRCNN和SRCNN算法相比，在图像纹理信息丰富的区域，使用本文方法得到的重建效果更好。

5 结束语

本文为了解决单帧图像能够在不同放大倍数的条件下得到更好的超分辨率重建效果，提出了一种Adam优化的卷积神经网络超分辨率重建方法。该方法首先使用ISODATA聚类算法对训练的图像集进行分类处理，然后在Adam优化的卷积神经网络中对输入图像进行特征提取和非线性映射得到特征映射图，最后在Adam优化的卷积神经网络中对特征映射图进行反卷积重建得到多尺度放大的重建图像。通过实验验证使用本文方法在不同放大倍数条件下的重构效果优于传统算法，在视觉效果上有较好的表现。

Fig.4 Butterfly reconstruction image in Set 5 image图4 Set 5中的蝴蝶重建对比图

Fig.5 Baboon reconstruction image in Set 14 image图5 Set 14中的狒狒重建对比图