三自由度柔索并联机构运动性能分析

张 龙, 牛 奔

(淮南师范学院 机械与电气工程学院， 安徽 淮南 232038)

0 引 言

柔索并联机构采用绳索替代刚性连杆作为驱动元件，与传统刚性并联机构相比，具有结构简单、工作空间大、负载能力强等特点[1-2]。自20世纪80年代以来，国内外学者对柔索并联机构做了大量研究。文献[3]设计了一种4根绳索牵引的移动摄像系统SkyCam，目前已被广泛应用于体育赛事的现场直播。文献[4]设计了一种针对户外环境下大型结构物搬运的新型柔索并联机构，开展了运动学、静力学和工作空间等方面的研究工作。文献[5-6]针对常规柔索并联机构和混合驱动柔索并联机构在运动学、动力学、工作空间等方面的差异，进行了深入对比研究。文献[7]在熔融沉积型(FDM)3D打印机的基础上，利用柔索并联机构的优点设计了一种柔索并联3D打印机，完成了运动学和动力学建模以及刚度分析，并进行了实验研究。

文中首先对三自由度柔索并联机构的组成和原理进行描述，完成运动学建模。然后依据静力学方程和矢量封闭原理，求出机构的可控工作空间，在此基础上，引入灵巧度和承载能力指标，分析机构的运动性能。最后在给定结构参数下，运用Matlab软件编程进行实例仿真验证。

1 运动学建模

1.1 机构描述

三自由度柔索并联机构如图1所示。

图1 三自由度柔索并联机构

图中，三自由度柔索并联机构由4根柔索和重物组成，Ai表示柔索的固定铰结点，P表示4根柔索与重物的铰结点，其中A1、A2、A3构成正三角形，A4位于△A1A2A3重心的正上方。定义坐标系{O}为全局坐标系，原点位于△A1A2A3的重心，x、y轴固定在△A1A2A3所在平面，z轴垂直于△A1A2A3所在平面，方向向上。△A1A2A3的边长为a，A4距△A1A2A3所在平面的高度为h。

1.2 运动学建模

由图1得柔索长度矢量

Li=OAi-OP=Ai-P，

(1)

式中:Ai----坐标系{O}原点到固定铰结点的矢量，i=1，2，3，4;

P----坐标系{O}原点到柔索与重物铰接点的矢量。

各条柔索的单位方向矢量为

(2)

各条柔索的长度为

Li=‖Li‖。

(3)

根据并联机构微分运动学有

(4)

式中:

柔索并联机构Jacobian矩阵为J，且满足

1.3 可控工作空间求解

柔索并联机构的可控工作空间定义为重物运动过程中满足受力平衡，且每条柔索拉力均大于零的所有位置的集合[8]。

对该柔索并联机构进行受力分析，根据重物的受力平衡关系得静力学方程

(5)

式中:Fi----柔索拉力，Fi=fiui，N;

FP----重物所受的外部作用力，N。

将式(5)写出矩阵形式,有

JT×F=W,

(6)

式中:JT----柔索并联机构Jacobian矩阵的转置矩阵。

W=-FP。

求解式(6)，得柔索拉力为

F=(JT)+W+[I-(JT)+JT]δ,

(7)

式中:(JT)+----矩阵JT的Moore-Penrose广义逆矩阵;

δ----任意一个列向量。

根据矢量封闭原理[8]，如果由重物位置计算出I-(JT)+JT中的每个元素均大于零，则牵引重物的柔索拉力大于零，也即该位置落在可控工作空间内。

2 运动性能分析

2.1 灵巧度分析

式(4)中的Jacobian矩阵J表示柔索牵引速度和重物运动速度之间的关系，即当给定重物速度，可以唯一确定四根柔索速度；但当给定柔索速度，则不能唯一确定重物速度。柔索并联机构处于奇异位形时，其运动状态无法确定，因此将衡量机构运动性能程度的指标称为灵巧度[9]。通常采用Jacobian矩阵J的条件数作为并联机构的灵巧度指标，即

(8)

式中:σmax、σmin----分别表示Jacobian矩阵J的最大奇异值和最小奇异值。

条件数ψ的区间为[1,+∞)，即ψ为1时，并联机构处于最佳运动性能。为易于问题的研究和计算，在此引入条件数指标

(9)

式中:当CI值为1时，Jacobian矩阵J的最大、最小奇异值相等，机构灵巧度最高；当CI值为0时，机构灵巧度最低。

2.2 承载能力分析

根据并联机构承载能力定义[10]，当柔索拉力F为单位矢量时，求解外部作用力‖W‖的极值。因此，运用拉格朗日乘子法设定拉格朗日方程

LW=FTGTGF-λW(FTF-1),

(10)

式中:λW----拉格朗日乘子，G= (JT)+。

拉格朗日方程极值存在的条件为:

(11)

结合式(11)，对式(6)右边取模，并展开

‖W‖2=FTGTGF=FTλWF=λW=GTG,

(12)

式中可以看出，要求解‖W‖的极值只需求解矩阵GTG特征值的极值，即

(13)

式中:λmin(GTG),λmax(GTG)----分别为矩阵GTG特征值的极小值和极大值。

‖W‖的极值越大，并联机构的承载能力越好。在此，文中将‖W‖max作为柔索并联机构的承载能力指标PI，并代入式(12)，经化简得:

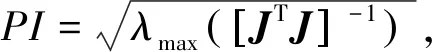
(14)

式中，PI值越大，表明柔索并联机构的承载能力越好。

3 实例仿真分析

3.1 运动学仿真分析

给定△A1A2A3的边长a=2 m，A4距△A1A2A3所在平面的高度为h=1 m。

采用Monte-Carlo方法，在MATLAB中编程仿真，求出该柔索并联机构的可控工作空间如图2所示。

图2 可控工作空间

从图中可以看出，三自由度柔索并联机构的可控工作空间呈三角锥形，随着高度增加，其切面面积逐渐减小。同时，在由3根支撑架组成的空间内，该柔索并联机构牵引重物所能达到的目标位置大多数集中在下半部分区域，因此在对该机构进行运动轨迹规划时，应使被牵引重物的运动轨迹尽量在可控工作空间的中下层且靠近中心的区域。

根据前述分析，定义重物在可控工作空间内的运动轨迹方程如下:

(15)

根据1.2的分析，通过MATLAB仿真得到柔索的长度和速度曲线分别如图3和图4所示。

图3 柔索长度曲线

图4 柔索速度曲线

由式(15)可知，被牵引重物在可控工作空间内的运动轨迹是一个水平圆。结合图3和图4可以看出，柔索长度和速度曲线的数值变化合理，轨迹连续光滑，与重物运动和柔索分布吻合，表明前述对该柔索并联机构的运动学分析正确。

3.2 运动性能仿真分析

柔索并联机构的运动性能与末端执行器所处的空间位置有关[11]，那么当文中所设计的柔索并联机构牵引重物的空间位置发生变化时，其运动性能也将产生相应变化。因此，根据前面分析得到的可控工作空间大小，选取能够涵盖工作空间低中高层不同切面对机构的运动性能进行分析，即被牵引重物的z坐标分别为0.2、0.4、0.6、0.8 m。

三自由度柔索并联机构对应上述4个切面的条件数指标CI分布图谱分别如图5～图8所示。

图5 条件数指标CI分布图谱(z=0.2 m)

图6 条件数指标CI分布图谱(z=0.4 m)

图7 条件数指标CI分布图谱(z=0.6 m)

图8 条件数指标CI分布图谱(z=0.8 m)

对比图5～图8可以看出，该柔索并联机构牵引重物在可控工作空间的中层和下层运动时，条件数指标CI值普遍大于其在上层运动时的值，且越靠近可控工作空间的中心，CI值越大。因此，三自由度柔索并联机构牵引重物运动时，如果重点考虑运动的灵巧度，应尽量设置被牵引重物的运动轨迹在可控工作空间的中下层区域，并远离边界区域，以保证获得较高的灵巧度。

该机构对应上述4个切面的承载能力指标PI分布图谱分别如图9～图12所示。

对比图9～图12可以看出，该机构承载能力指标PI值随运动高度的增加而减小，且越靠近可控工作空间的中心，PI值越小。因此，三自由度柔索并联机构牵引重物运动时，如果重点考虑机构的承载能力，应尽量设置被牵引重物的运动轨迹在可控工作空间的中下层区域，并远离中心区域，以保证获得较大的承载能力。

图9 承载能力指标PI分布图谱(z=0.2 m)

图10 承载能力指标PI分布图谱(z=0.4 m)

图11 承载能力指标PI分布图谱(z=0.6 m)

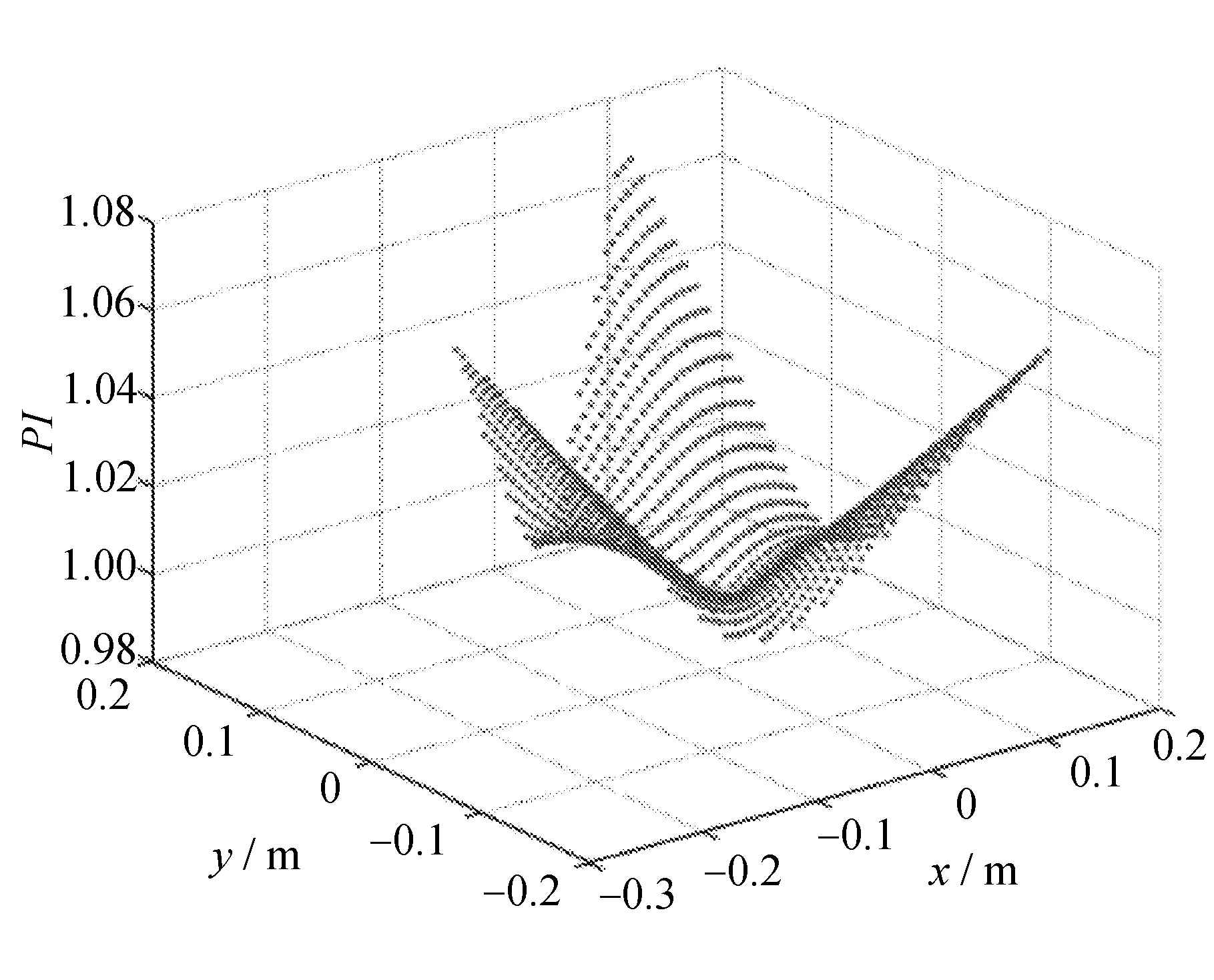
图12 承载能力指标PI分布图谱(z=0.8 m)

4 结 语

1)建立了三自由度柔索并联机构的运动学模型，并根据静力学方程和矢量封闭原理求解出该机构的可控工作空间。

2)在运动学分析的基础上，分析了三自由度柔索并联机构的运动性能，引入了灵巧度和承载能力指标。

3)实例仿真结果验证了理论分析的正确性，为后续进行机构动力学分析、样机研制和实验研究奠定了理论基础。