学生的审题能力为什么那么弱——“分段计费”一课观课反思

◇常立钢

本文的教学内容是人教版教材五年级上册第16 页“分段计费”。

教学片段：

师：请仔细观察图1，从收费标准中你得到了哪些信息？和你的同桌交流一下。

图1

师：“3 千米以内7 元”是什么意思？

生1：行驶3 千米一共花了7 元。

生2：不对，应该说3 千米以内，都是7 元。

师：你能举个例子说一下吗？

生2：哪怕行2 千米，也是7 元，不管多少，只要3 千米以内都是7 元。

生3：比如说2.5 千米，也是7 元。

师：正好3 千米呢？

生4：也是7 元。

师：超过3 千米，这句话如何理解？

生：如果行7 千米，就把3 千米去掉，剩下的部分就是超过3 千米的部分。

师：不足1 千米按1 千米计算，如何理解？

生：比如0.9 千米不到1 千米，也按1 千米计算。

师：同学们看（课件逐渐出示图2），我们可以把收费标准分成两段来计费，一段是“3 千米以内”，费用是7 元；一段是“超过3 千米的部分”，每千米1.5 元，0.3 千米也是1.5 元。你们明白这道题的“收费标准”了吗？

生：（齐）明白了！

图2

观课思考：

不可否认，在以上教学片段中，教师讲得非常清晰！ 教师将题意的理解分成了三个部分，分别是“3 千米以内”“超过3 千米的部分”“整体介绍分段计费”，教师善于引导学生用举例子的方式来理解“收费标准”，在“整体介绍分段计费”时，教师出示了直观图，学生一眼就看明白了“收费标准”。这样的教学，教学思路清晰，学生听得明白，不用怀疑，接下来的“列式与解答”，学生掌握得是非常好的。

但是，我们把解决问题的“审题”方法讲得如此清楚，为什么学生独立面对复杂信息时却表现得束手无策呢？针对某校五年级学生的调研测试结果显示，如果这道“应用题” 是教材上的“题型”，学生的解答正确率可以达到85%以上，可是，如果换成“复杂的信息、陌生的情境”，学生的解答正确率还不到30%。主要表现在，大部分学生一见到陌生的题，干脆就不做了，个别访谈时发现，这部分学生不会“审题”，不会圈圈点点，找出信息中的重点，不会通过画一画，让信息直观起来，不会把信息有条理地排列一下，以加深对信息的理解。

所以，我们再回头审视一下刚才的教学片段，对于学生的“审题”，教师“包办”太多，没有放手让学生独立面对复杂的信息，而是将难点“切割”成“小块儿”，学生不费力气就可以理解题意，长此以往，就会造成学生审题能力变弱。

因此，我们在解决问题教学中，要放手给学生独立审题的机会，通过恰当的引导，提高学生面对陌生情境时分析题意的能力，从而实现“获得分析问题和解决问题的一些基本方法”的课程目标。

重新设计：

师：同学们，首先我们要认真读一下题目，看看从收费标准中你得到了哪些信息。不过，怎样读题才算是“认真”的呢？关于“读题”，你有什么好的方法？

生：在信息上圈画出重点。

生：将信息有条理地整理一下。

生：画画图，让信息更明白。

师：这些同学的方法真好，请你们选一种方法读一读题目，看看谁能将收费标准讲得更清晰。

（学生活动）

生：我把收费标准整理成两种情况，一种情况是“3 千米以内”，另一种情况是“超过3 千米的部分”。（如图3）

图3

师：他整理得真清楚，谁来解释一下“3 千米以内”的标准？

生1：行驶3 千米一共花了7 元。

生2：不太对，应该说3 千米以内，都是7 元。师：谁能解释得更清楚？

生3：请看我画的图（如图4），哪怕行2 千米，也是7 元，不管多少，只要3 千米以内都是7 元。

图4

师：用画图的方法来解释，看得更明白！

师：谁能结合你画的图来解释一下“超出3千米的部分”的标准？

生：如果行7 千米，就把3 千米去掉，剩下的部分就是超过3 千米的部分。

生：这部分路程每千米按1.5 元计算，不足1千米按1 千米计算，比如0.9 千米不到1 千米，也按1 千米计算。（如图5）

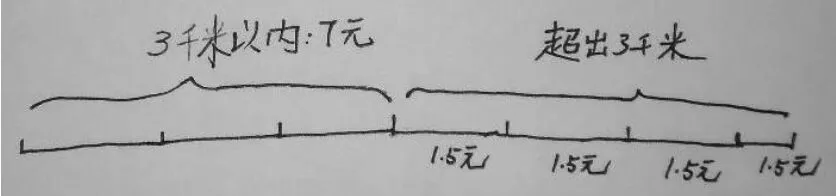
图5

……

在上面的教学设计中，教师并没有按照自己的想法直奔主题，引导学生去理解所谓的重点语句，而是放手让学生自己选择一种方法去读题，读题的时候围绕如何读得更明白积极主动地想办法。 当部分学生在读题时遇到不理解的情况时，教师适时地将问题抛向其他学生，引发生生互动，从而引导学生主动地运用画图策略来理解题意。