有向双环网络的移动路由拓扑对称构造算法

孙灏

摘要：在采用二叉树模型构建的有向双环网络路由模型的基础上，研究有向双环网络的移动路由拓扑对称构造算法，通过二叉树模型处理有向双环网络路由问题，确定有向双环网络的紧优对称无限簇，处理有向双环网络的最佳路由拓扑对称问题;采用双环拓扑优化算法模拟计算有向双环网络移动路由拓扑，确定最佳双环网络拓扑;并研究移动路由分布式容错算法，当有向双环网络内个别节点出现故障时，提升路由算法的坚定性，使其发挥最优化拓扑性能。通过同相关路由构造算法的对比，证实了该路由构造算法具有网络延迟上升速度低、吞吐量高的优势。综上所述，表明该算法具有较高的拓扑性质和通信性能。

关键词：有向双环网络;移动路由;拓扑;对称;构造算法;容错算法

中图分类号：TP302文献标志码：A

文章编号：2095-5383（2019）02-0046-05

Abstract：Efficient internet topology is of great significance for improving the efficiency and quality of information interaction in the information age. On the basis of using the binary tree model to construct the routing model of directional double-loop networks，the topology symmetric construction algorithm for mobile routing of directional double-loop networks was studied. In this paper，the routing problem of directional double-loop network was dealt with the binary tree model，the compact excellent symmetric infinite cluster of directional double-loop network was determines，and the topology symmetry problem of optimal routing of directional double-loop network was solved. The algorithm of double loop topology optimization was used to calculate the mobile routing topology of the directed double loop network. In this paper，the distributed fault tolerant algorithm of mobile routing was studied to improve the firmness of routing algorithm in case of fault of individual nodes in the dual loop network. The comparison with the correlation routing algorithm proves that the proposed routing algorithm has the advantages of low latency and high throughput. In summary，it is shown that the algorithm has high topological properties and communication performance.

Keywords： directional double-loop network; mobile routing; topology; symmetry; construct algorithms; fault-tolerant algorithm

在互聯网技术越发成熟的今天，受多处理机系统规模不断发展的影响，计算机系统结构的通信效率逐渐引起人们的关注。为了提高人们通过网络进行信息交互的效率和质量，相关人员致力于寻找一种拓扑结构简单、网络直径短且连接度低的移动路由拓扑结构[1]。在计算机互联网络与通信系统内，双环网络是主要的拓扑结构[2]。文献[3-5]描述的均是有向双环网络最佳跳跃在满足给定范围条件下的最优路由算法，此类算法在节点失效等故障条件下，路由坚定性较差，无法发挥最优化拓扑性能。因此，本文研究了新的有向双环网络的移动路由拓扑对称构造算法，处理有向双环网络的最佳路由拓扑对称问题，在获取有向双环网络移动路由最佳拓扑的基础上，研究其分布式容错算法，提升有向双环网络移动路由拓扑结构的性能。

1 有向双环网络的移动路由拓扑对称构造

1.1 构建有向双环网络路由模型

假设有向双环网络为GN;r，s（各顶点分别是0，1，2，…，N-1），以各顶点i为出发点的两条有向边分别记作i→i+rmod N和i→i+smod N，r与s均为自然数，并满足1

以往求解有向双环网络直径时，多基于有向图L形瓦的特征参数进行计算，然而L形瓦只能间接表现各节点的路由特征。因此，采用二叉树模型反映有向双环网络GN;r，s内各节点的最佳路由特性，二叉树模型的树高与有向双环网络GN;r，s的直径一致，通过确定有向双环网络GN;r，s紧优对称点r，s解决其最优路由对称问题。

用+r、+s表示有向双环网络各节点发出的有向边i→i+rmod N和i→i+smod N，由于有向双环网络具有对称性[7]，节点U与节点V间距离同节点O与节点V-U间距离一致。因此，在分析有向双环网络GN;r，s的路由策略时仅分析O节点与其他节点间的了路由策略即可，一般情况下i的初始值为0。

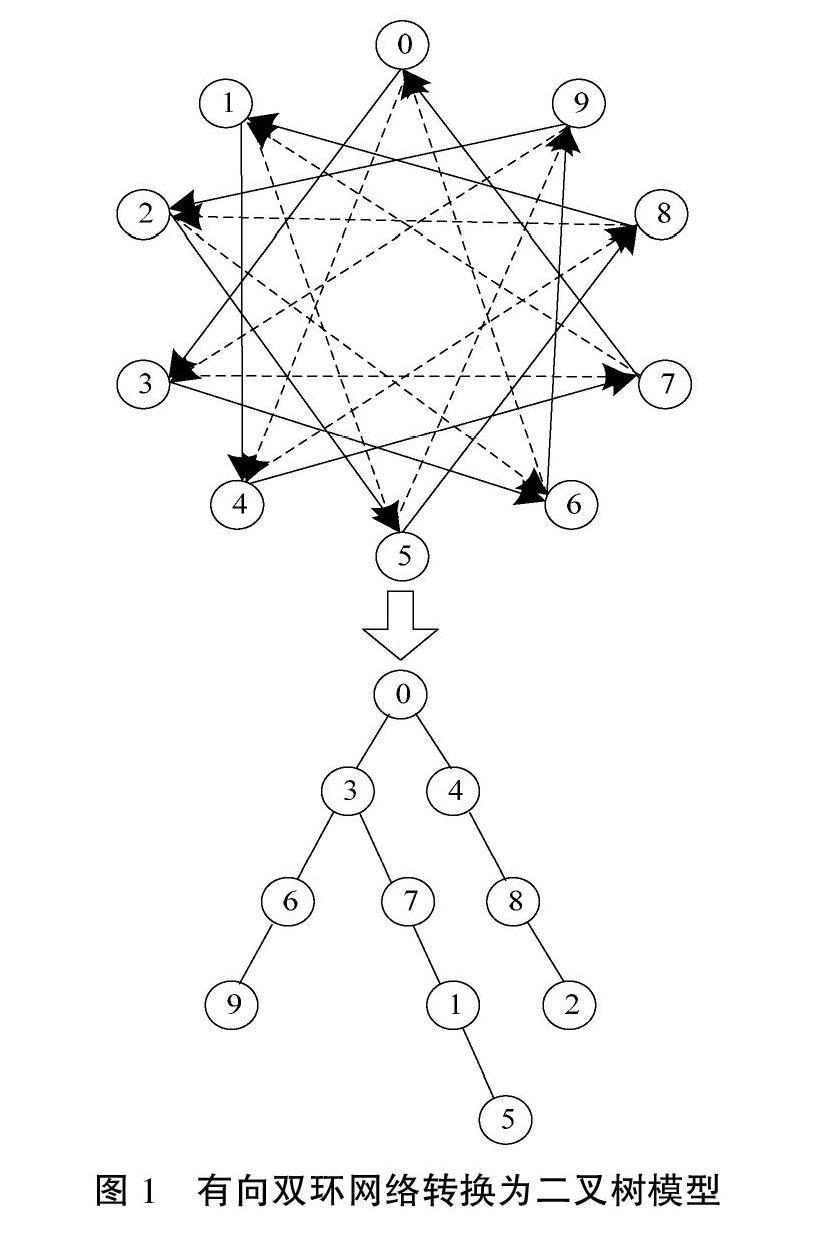
定义1：在节点集U内，以节点O为根节点，+r边和+s边为连线，r和s分别为根节点的左孩子和右孩子，搭建二叉树模型第一层节点。在第一层节点中按序取各节点i，通过i+rmod N与i+smod N确定节点i的左孩子节点与右孩子节点。当节点集U内不存在孩子节点时，需在二叉树模型下一层内构建节点i的孩子节点，且将其保存至节点集U内，否则无动作。循环此过程，通过上一层的全部节点生成下一层节点，直至无法生成新节点结束，构建的二叉树模型用BTN;r，s表示。有向双环网络G10;3，4转换为二叉树模型BT（10;3，4）如图1所示。

1）初始化同时构建根节点。给定N，确定dN;r，s的直径下界1bN;构建根节点，其值data和层数layer均为0;在节点集数组N内写入根节点值;定义保存紧优对称点r，s个数的变量

2）确定紧优对称点r，s。分别由2至N-2和由r+1至N-1外层循环r和内层循环s，并分别取值;在N内节点数量低于N的条件下，按序取当前层内各节点，通过data+rmod N生成左孩子节点，通过data+smod N生成右孩子节点;层数提升1，再次进行左、右孩子节点生成过程，至无法生成新节点或N内节点数量等于N结束;当N内节点数量等于N时，对比1bN值与层数值，在两值相等的情况下，输出紧优对称点值并存储，同时在变量sum上加1，再次进行外层循环和内层循环过程，至外层循环结束为止。

3）确定N、1bN、全部紧优对称点以及紧优对称点总数，并输出。外层r、中层s和内层分别从2至N-2、r+1至N-1和当前层上第一个阶段至最后一个节点循环，时间复杂度和空间复杂度分别为On3和On。

此算法功能为：针对任意N值，确定有向双环网络全部紧优对称点，可在有限时间内确定任一N值的全部紧优对称点。

通过二叉树模型处理有向双环网络G（N;r，s）的路由问题，可快速获取有向双环网络直径的显示公式，确定有向双环网络的紧优对称无限簇，处理有向双环网络的最佳路由对称问题。

1.2 有向双环网络移动路由拓扑模拟计算及分析

上述过程成功构建有向双环网络，用dmin表示有向双环网络直径最小值，为使该有向双环网络拓扑达到最佳状态，也就是使有向双环网络直径最接近dmin，需确定以h表示的有向双环网络移动路由的最佳跳跃[11]。在确定h的过程中，采用双环拓扑优化算法，针对已知N，构建h、x（有向双环网络边缘长度）有所差异的有向双环网络。确定不同有向双环网络内的d1与d2，进行对比，将最大者作为d。确定N内全部的dmin，当d=dmin时，确定a表示的有向双环网络平均跳跃距离，同时确定全部可能的d=dmin或最小d相应的a，确定最小值，其相应的h为有向双环网络最佳h。双环拓扑优化算法适用于全部N，通过双环拓扑优化算法对2.1小节内的有向双环网络实施模拟运算，确定可靠最优有向双环网络移动路由拓扑参数（3≤N≤104），参数内涵盖各已知N的h、d和a。

最佳双环拓扑参数具有如下规律：

1）在N≠3.5的条件下，基于有向双环网络对称性，其具最佳h有偶数个[12]，因此最佳h个数≥2，使有向双环网络移动路由拓扑达到最优化。也就是最佳h以2的倍数出现，假设h为最佳状态，那么1-hmod N同同样为最佳状态，同时基于N+1/2对称，其任意两值相加均等于N+1。

2）通常情况下，N的大小同d与a的大小呈正比;在同一N内，d与a的大小呈正比;在同一N内，d一致条件下，a也一致。

（3）特殊情况下，个别N内确定最佳h的解析式的个数为有限个。

（4）在3≤N≤104条件下，d的上限为：

通过双环拓扑优化算法，能够确定全部N（N>104）的d与a，也就是确定全部N的最佳双环网络拓扑，d与a为准确解。

1.3 移动路由分布式容错算法

移动路由选择算法直接关系着有向双环网络的拓扑性能，对故障条件下有向双环网络移动路由的容错算法进行分析研究，能够提升有向双环网络移动路由算法的坚定性，发挥其最优化拓扑性能。在有向双环网络内节点失效等价于链路失效[13]，因此只研究节点失效状态即可。通过由部分区域中地址表情报固定时间内循环互换实现移动路由分是容错算法的自适应性[14]。在有向双环网络内个别节点出现故障的条件下，与故障节点距离最近的上游节点向系统发送故障信息，通知相关各节點于各自地址表中对故障节点地质好实施修正，如标识为“∞”，使信包在寻径过程中不接触故障节点。

1）算法1：

规则1：有向双环网络内随意节点获取的信包目的地址同自身地址一致条件下，接收此信包。

规则2：假设信包的目的地址是部分区域地址表内本节点意外的任意节点，同时抵达该节点的路径中不存在故障节点，那么通过短链传送信包;相反：在远亲节点未出现故障条件下，通过长链传送信包;在远亲节点出现故障，邻近节点未出现故障条件下，通过短链传送信包[15]。

规则3：假设信包的目的地址是远程地址表内的任意节点，同时抵达该节点的路径中不存在故障节点，那么通过长链传送信包;相反：在邻近节点未出现故障的条件下，通过短链传送信包;在邻近节点出现故障，远亲节点未出现故障条件下，通过长链传送信包。

规则4：假设信包的目的地址是部分区域和远程地址表外的任意节点，那么在目的地上游出现故障的条件下，邻近节点无故障时，通过短链传送信包;邻近节点出现故障，远亲节点未出现故障时，通过长链传送信包。在目的地上游未出现故障的条件下，远亲节点未出现故障时，通过长链传送信包;远亲节点出现故障，近邻节点未出现故障时，通过短链传送信包。

2）算法2

规则1：假设获取信包的目的地址同本节点地址一致，那么接收信包。

规则2：对有几率存在路由的目的节点最小坐标值I，J实施计算。

规则3：寻找到达目的节点的路径。假设纵坐标低于最大值，远亲节点有效，同时未确定路由

（Y1=1），那么纵向寻找，且重复此过程;假设横坐标低于最大值，紧邻节点有效，用时未确定路由（Y1=1），横向寻找，同时转向纵向寻找过程;假设纵、横坐标不低于最大值，那么说明路由以确定（Y1=0）;依照寻找路径返回，至纵坐标值降低1结束，同时转向横向寻找过程;假设Y1=0，则记忆第一步寻找方向。

规则4：假设Y1=0，则通过记忆方法寻径。

规则5：假设Y1=1，则转向规则2。

2 实验分析

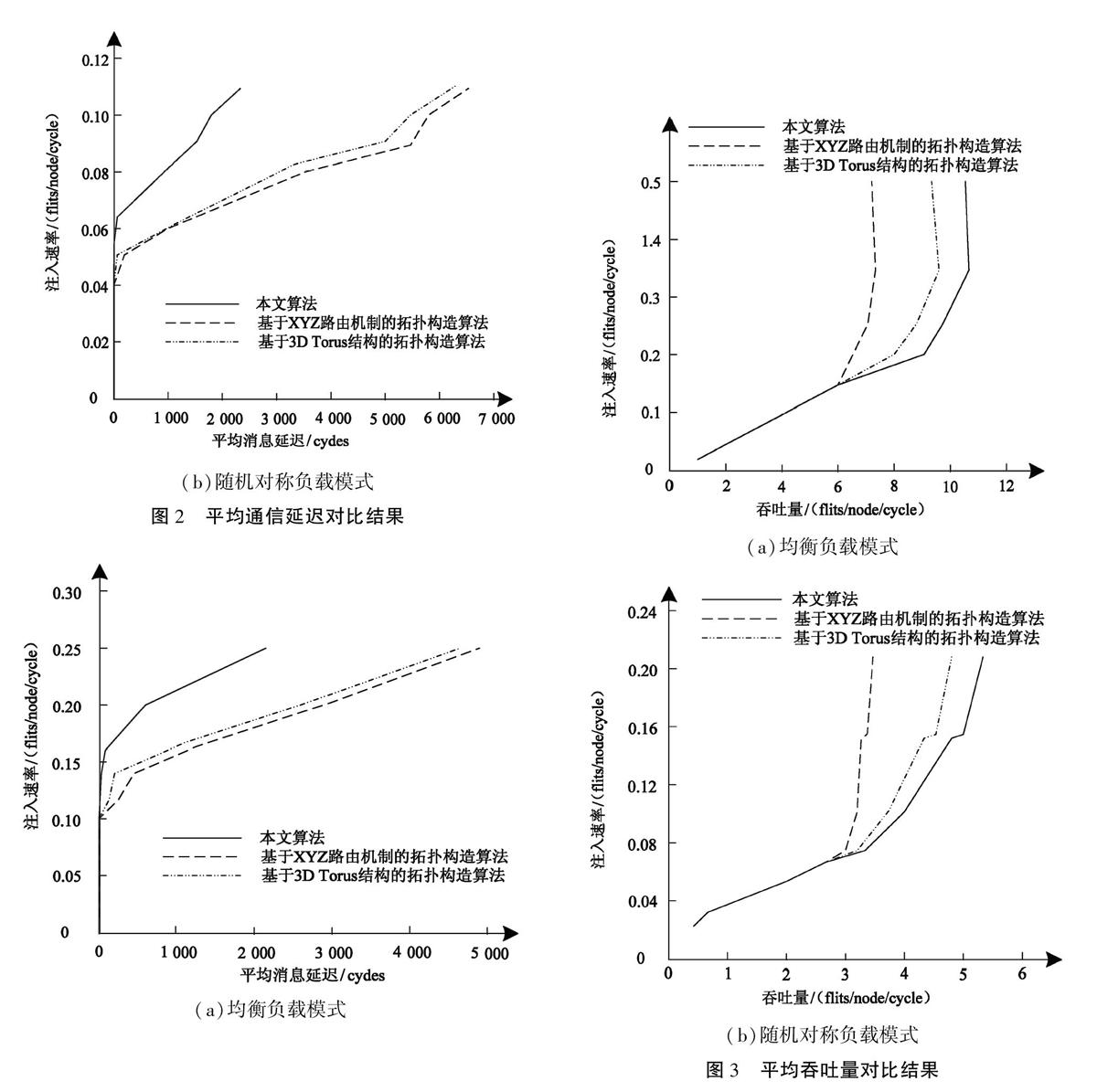
平均通信延迟与平均吞吐量是拓扑构造算法中较为关键的性能参数。实验为验证本文提出的有向双环网络移动路由拓扑对称构造算法的性能，选取1条虚信道，将交换机制、链路速率和参数分别设置为虫孔交换、10 Kb/s和125个。对比本文算法、基于XYZ路由机制的路由拓扑构造算法和基于3D Torus结构的拓扑构造算法的平均通信延迟与平均吞吐量，结果如图2和图3所示。

由图2可得，均衡负载模式下，在注入率低于0.11 flits/node/cycle的条件下，三种算法的延迟均较低，且差距较小;在注入率达到0.16 flits/node/cycle的条件下，三种算法的网络延迟均逐渐上升，但本文算法的网络延迟上升速度相较于其他两种算法有显著降低。随机对称负载模式下，在注入率低于0.046 5 flits/node/cycle的条件下，三种算法的延迟均较低，且差距较小;在注入率达到0.061 4 flits/node/cycle的条件下，注入率一致时，本文算法的平均消息延迟明显小于其他两种算法。

由图3可得，均衡负载模式下，在注入率低于0.15 flits/node/cycle的条件下，单位时间内三种算法获取的数据包一致;在注入率高于0.15 flits/node/cycle的条件下，有向双环网络的饱和吞吐量是11 flits/node/cycle;随机对称负载模式下，在注入率高于0.059 flits/node/cycle的条件下，基于XYZ路由机制的拓扑构造算法吞吐量趋于饱和，而本文算法吞吐量在注入率达到0.15 flits/node/cycle的条件下才趋于饱和，并且本文算法吞吐量与其他两种算法相比，有显著提升趋势。图2和图3的综合结果表明，本文算法的平均通信延迟低、平均吞吐量高，通信性能优于对比算法。

3 结论

本文提出有向双环网络的移动路由拓扑对称构造算法，利用二叉树构建有向双环网络，处理有向双环网络的最佳路由拓扑对称问题后，对有向双环网络移动路由拓扑进行模拟计算及分析，并对故障条件下有向双环网络移动路由的容错算法进行分析研究，增强有向双环网络移动路由算法的坚定性。经实验证明，本文算法的性能较好，可提升有向双环网络移动路由拓扑结构的性能。

参考文献：

[1]ILYUSHIN G D，PISAREVSKII Y V.Modeling of the self-organization processes in crystal-forming systems： Symmetry and topological code of cluster self-assembly of molecular （island） and framework MT structures of vanadyl sulfates[J].Crystallography Reports，2015，60（6）：776-790.

[2] 张玲，聂少华.基于粒子滤波步行长度预测的移动ad hoc网络路由算法[J].电讯技术，2016，56（3）：331-336.

[3] 李贞妮，李晶皎，王爱侠，等.一种新型片上网络拓扑结构及其自适应路由算法[J].东北大学学报（自然科学版），2017，38（9）：1217-1221.

[4] 徐吉兴，李建波，由磊，等.一种基于移动方向的容延迟网络受控传染路由算法[J].小型微型计算机系统，2015，36（1）：60-66.

[5] 佟宁，浑洁絮，杨琦，等.基于多层立方体簇结构的3D-Ad hoc 网络路由算法[J].计算机工程与应用，2016，52（15）：135-140.

[6] 向敏，唐亮，王平.基于Dijkstra能量均衡的无线HART图路由算法[J].仪器仪表学报，2016，37（11）：2628-2636.

[7] SHEVCHENKO V Y，BLATOV V A，ILYUSHIN G D.Symmetry and topology codes of cluster self-assembly for icosahedral structures of the NaZn 13-cF 112 and TRB 66-cF 1944 family[J].Glass Physics & Chemistry，2015，41（4）：341-351.

[8] 耿海军，施新刚，王之梁，等.基于有向无环图的互联网域内节能路由算法[J].计算机科学，2018，45（4）：112-116.

[9] 佟宁，浑洁絮，李寒.三维无线自组网络的成簇及自适应路由算法[J].小型微型计算机系统，2015，36（3）：508-513.

[10] 李梅，武海燕，奚建清，等.基于改進的遗传算法的MANET最优路由生成方法[J].电子技术应用，2017，43（8）：119-122.

[11] 涂丽芳，张姿，黄廷磊.基于平滑移动模型的k连通网络拓扑控制算法研究[J].计算机应用研究，2015，32（8）：2465-2468.

[12] 王俊士.移动通信网络路由缓冲区溢出修复优化仿真[J].计算机仿真，2016，33（5）：200-203.

[13] 丁毓良，张剑贤，周端，等.直线引导的Torus结构路由算法[J].计算机工程与科学，2017，39（2）：275-279.

[14] 宋有关，李建波，和天玥，等.基于节点相似性的容迟网络概率路由算法[J].计算机工程，2016，42（9）：63-70.

[15] ILYUSHIN G D.Modeling of self-organization processes in crystal-forming systems： symmetry and topology code for cluster self-assembly of crystal structures for molecular and framework compounds [J].Russian Journal of Inorganic Chemistry，2015，60（13）：1626-1691.