辩证法的“运动”论题和“芝诺佯谬”之解决——与张华夏教授商榷①

陈晓平12

(1.华南师范大学 公共管理学院,广东 广州 510006;2.广东财经大学 智能社会与人的发展研究中心，广东 广州 510320)

张华夏教授指出：“黑格尔矛盾辩证法有两个论题：(1)运动的本质就是矛盾，‘某物之所以运动是因为它在同一个‘此刻’在这里，又不在这里。’(2)存在的本质就是‘某物’与‘他物’的对立统一。……这两个论题是黑格尔的致命伤。”[1]1对此，笔者持不同观点。本文仅就第一个辩证论题与张华夏教授进行商榷，并以此为契机，对辩证法及其有关的数学概念和准则给以较为深入的探讨。

一、辩证法的运动论题及张华夏的批评

黑格尔断言“矛盾是一切运动的本质”。黑格尔在其《逻辑学》中谈道：“外在的感性运动本身是矛盾的直接实有。某物之所以运动，不是因为它在这个‘此刻’在这里，在那个‘此刻’在那里，而是因为它在同一个‘此刻’在这里，又不在这里；因为在同一个‘这里’，它在并且不在那同一时刻。”[注]黑格尔：《逻辑学》(下卷)，杨一之译，商务印书馆，2013年版，第66-67页。参阅英文版，G.W.F.Hegel, The Science of Logic.Cambridge University Press.P382。张华夏正确地指出，杨一之把“某物之所以运动，不是因为它……”错译为“某物之所以运动，不仅是因为它……”。这里采纳了张华夏教授的翻译。

对黑格尔这段论述，恩格斯在《反杜林论》中给以进一步阐述。他说：“当我们把事物看作是静止而没有生命的、各自独立、相互并列或先后相继的时候，我们在事物中确实碰不到任何矛盾。……如果限于这样的考察范围，我们用通常的形而上学的思维方式也就行了。但是一当我们从事物的运动、变化、生命和相互作用方面去考察事物时，情形就完全不同了。在这里我们立刻陷入了矛盾。运动本身就是矛盾；甚至简单的位移之所以能够实现，也只是因为物体在同一瞬间既在一个地方又在另一个地方，既在同一个地方又不在同一个地方，这种矛盾的连续产生和同时解决正好就是运动。”[2]160

对于黑格尔和恩格斯关于运动的辩证观点，张华夏教授在其文章中提出质问：“同一瞬间既在一个地方(S1)又在另一个地方(S2)，这意味着什么？意味着运动是不需要时间的”，紧接着，他用如下公式来说明“不需要时间的”运动速度：

张华夏教授评论说：“这公式表明，运动的速度有多大？无限大？这无论在数学上还是力学上都是无意义的和不可能的。可惜黑格尔的哲学继承者们并不了解数学哲学的点的抽象(欧几里得提出，公元前300年)、极限论(如柯西1821年出版的《分析教程》中论证的)与实数连续统(德国数学家魏尔斯特拉斯，于1860创立的理论)是什么意思，与这个问题有什么关系，第二次数学危机是怎样获得解决？而认为可以用矛盾论来解决。”[1]2

张华夏教授在引用黑格尔那段话之后强调：“这里我们特别要注意，黑格尔谈的‘此刻’用的是英文的‘now’或‘instant’，是没有片刻的‘时点’；而here，there，是欧几里得几何学中只有位置没有长宽高的‘地点’或位置。”[1]1

总之，张华夏教授试图借助于现代数学把黑格尔和恩格斯关于运动的辩证法论题彻底否定。然而，在笔者看来，张华夏教授的论证是缺乏说服力的；恰恰相反，从现代数学的角度看，辩证法的运动论题在实质上是可以成立的，尽管在表述上可以改进。

二、对辩证法的运动论题给以初步辩护

张华夏教授对辩证法运动论题的批评虽然富有启发性，但却难以令人信服。首先，黑格尔和恩格斯所说的“此刻”和“这里”肯定不是欧几里得所谓“没有长宽高的点”，不是因为他们不懂得，而是因为他们故意不用。在他们的辩证法学说中，欧几里得几何这类初等数学如同形式逻辑属于形而上学的思维方式，常常成为他们批评的对象；他们所推崇的是微积分这类高等数学，只有此类高等数学才能体现辩证法的思维方式。尽管笔者不同意黑格尔和恩格斯对形式逻辑的过分贬低，但对他们揭示高等数学的辩证法特征表示赞同。恩格斯谈道：

“因为辩证法突破了形式逻辑的狭隘界限，所以它包含着更广的世界观萌芽。在数学中也存在着同样的关系。初等数学，即常数数学，是在形式逻辑的范围内活动的，至少总的说来是这样；而变数的数学——其中最重要的部分是微积分——本质上不外是辩证法在数学方面的运用。[2]132

在恩格斯看来，把“此刻”“这里”看作没有长度或体积的点，相当于用常数0来刻画它们，那是抽象的存在，属于形而上学。与之不同，辩证法则是把时间和空间上的点当作具体的存在，它们不是常数0，而是作为变数的无穷小。无穷小是微积分的关键概念，“本质上不外是辩证法在数学方面的运用”。可见，张华夏把黑格尔和恩格斯所说的“时刻”和“地点”看作没有长度或体积的欧几里得点，肯定是一种错位或误解。

其次，既然黑格尔特别是恩格斯是从微积分的角度考虑运动之本质的，那么对他们的批评也应当立足于微积分。然而，从微积分得不出“运动不需要时间”的结论，即张华夏所质疑的那个分母为0的公式不是微积分所能推导出来的。这意味着，张华夏教授对辩证法运动论题的批评缺乏根据，甚至有强加之嫌。

我们知道，微积分所说的瞬时速度是距离(位移)对时间的导数dy/dx，其分母和分子都是无穷小而不是0。具体地说，分母dx代表瞬时(时间的微分)，它是大于0的无穷小；分子dy(或df(x))即位移的微分，代表瞬时所走过的距离，也是大于0的无穷小。在微积分的语境中，“同一时刻”就是同一无穷小的时间间隔，“同一地点”就是同一无穷小的空间间隔，并且无穷小不是一个常数，而是一个以0为极限的变数。这样，辩证法关于运动的论题——“运动是在同一瞬间既在一个地点又不在一个地点”——便不是不可理解的，既然这里的“瞬间”和“地点”都不是常数而是变数。

为什么说无穷小是一个变数而不是常数？我们知道，常数不外乎两类即0和非0，而无穷小不属于其中任何一类。无穷小不等于0，否则无穷小不能作除数，而在微积分的运算中无穷小dx是可以作除数的。无穷小不是非0的任何一个常数，因为只要给出任何一个非0的常数，无穷小都比它的绝对值要小，这正是无穷小的定义。这意味着，如果把无穷小作为一个常数，那么它是违反形式逻辑的排中律的，即它既不是0也不是非0；相应地，它也是违反矛盾律的，即无穷小既是0又是非0。为了不违反形式逻辑，无穷小只能是一个变数，这个变数在数轴上所对应的不是一个点，而是一个间距为无穷小的变化区间。

19世纪法国数学家柯西(A.Cauchy,1789-1857)给出“无穷小”的比较精确的定义，其定义的本质就是把无穷小量表述为一个变量x而不是常数，其变化区间是：0<│x│<δ，δ是一个任意小的正数。柯西在其《分析教程》中指出：“当同一变量逐次所取的绝对值无限减小，以致比任何给定的数还要小，这个变量就是所谓的无限小或无限小量，这样的变量将以0为极限。”[3]195柯西明确地把无穷小看作一个变量，0是无穷小的极限而不是无穷小本身。

关于极限，柯西给出这样的定义：“当同一变量逐次所取的值无限趋向于一个固定的值，最终使它的值与该定值的差要多小就多小，那么最后这个值就称为所有其他值的极限。”[3]195在这里，“它的值与该定值的差要多小就多小”是指无穷小，无穷小是一个变数；那个被趋近的“定值”就是极限，极限是一个常数。柯西的极限概念奠定了微积分的理论基础，一直沿用至今。本文将表明，把极限仅仅局限于常数，是导致多种数学困境的根源，也是使“柯西极限存在准则”不被作为公理而需进一步“证明”的原因。

关于运动问题，如果把任意小区间0<│x│<δ中的x作为瞬时，那么相应的位移函数f(x)就处于一个无穷小的空间，即0<│f(x)│<ε，ε也是一个任意小的正数。据此，我们可以说，位移运动的物体在同一时刻既在一点又不在一点，因为这里的“时刻”和“地点”都是无穷小的变量，而不是常量。进而言之，微积分中表示“瞬时速度”的导数dy/dx(即df(x)/dx)，一般是一个不为0的数，这意味着运动是在瞬时走过一段不为0的距离；在此意义上可以说，其起点和终点不在同一个地方。这便初步支持了辩证法的运动论题，即：运动在同一时刻既在一个地点又不在一个地点。

为什么把以上论证说成是“初步”的辩护呢？因为它所为之辩护的运动论题在表述上还比较粗糙，甚至看上去是违反形式逻辑的。本文将试图改进辩证法的运动论题，消除其违反形式逻辑的表达方式。

正如高等数学与初等数学的关系，辩证法不是对形式逻辑的否定，而是对形式逻辑的超越；辩证法绝不违反形式逻辑，但它不限于形式逻辑。然而，黑格尔甚至恩格斯常常把形式逻辑看作辩证法的对立面而加以批评，这是严重失当的。正因为此，他们关于辩证法的论述存在不少牵强附会的地方。张华夏教授对他们的辩证法论题的批评并非完全没有道理，但是走过头了，走到用形式逻辑来否定辩证法的另一个极端。笔者则试图行走一条“中庸之道”，保留辩证法论题的精神实质，但改变其违反形式逻辑的表述方式。

三、关于有理数和无理数的哲学问题：实无限与潜无限

其实，关于运动的哲学问题早在古希腊就以“芝诺佯谬”的方式被提出。虽然借助于辩证法的运动论题可以在一定程度解决“芝诺佯谬”，但是，以违反形式逻辑的方式来解决“芝诺佯谬”是难以令人满意的。笔者认为，“芝诺佯谬”的症结在于对空间和时间“无限可分”和连续性的错误理解，而这种错误理解在数学中也是根深蒂固的，体现在对实数连续性的阐述上，其中涉及有理数和无理数、实无限和潜无限等重要概念。因此，澄清这些概念对于芝诺佯谬的恰当解决以及对辩证法运动论题的深入理解，都是至关重要的。

无理数是相对于有理数而言的。有理数被定义为一个整数a和一个正整数b的比，即a/b。之所以要求分母b是正整数，是要以b为比较的标准，即衡量单位的集合；要求分子a为整数，是要它可与b中的a个单位相重合，从而成为可度量的。可见，有理数的根本特征就是可度量性；可度量性反映在数轴上就是：每一个有理数对应一个确定的点。

与之不同，无理数不能表达为整数比a/b，因而不具有可度量性。其不确定性的另一种表现是：若将它写成小数形式，小数点之后的数字有无限多个，并且是不循环的，即无限不循环小数。显然，无限不循环小数在数轴上没有一个确定的点与之对应，只有一个无穷小的区间与之对应。这是无理数在数轴上不同于有理数的地方。

在教科书中，有理数又可分为有限数(整数和有限小数)和无限循环小数。每一个无限循环小数对应于一个常数(整数比)，如0.3333……对应于1/3；每一个有限数(0除外)对应于一个以9为循环节的无限循环小数，如2.5对应于2.4999……，1对应于0.9999……；加之规定0表示为0.000……，这样，作为整数比的有理数和无限循环小数之间具有一一对应的关系。再把作为无限不循环小数的无理数考虑在内，便可说：“任何实数都可用一个确定的无限小数来表示。”[4]1不过，在笔者看来，这个说法是有问题的，现分析如下。

无限循环小数是趋近于某个整数比(整数是分母为1的整数比)的无穷过程，那个整数比是该无穷循环小数的极限；或者说，每一个整数比都是一个极限，它被一个无穷循环小数所趋近。需强调，无限趋近的过程是无休止的，而极限则是一个确定的常数即整数比，因此二者之间并不相等，只是具有某种对应的关系。

然而，通常教科书把无限循环小数和它所对应的整数比看作相等的，[4]1-2如0.3333……=1/3。如果说这个等式的不恰当性还比较隐蔽，那么，该等式两边同乘以3而得到0.9999……=1，则是明显不妥的。正确的表达式应是：0.9999……=1―δ(δ→0)。相应地，前一等式应该改为：0.3333……=1/3―δ(δ→0)。在这里，δ是一个变数即无穷小，无穷小以0为极限，但不等于0。相应地，无限循环小数也是一个变数，如，0.9999……是以1为极限的变数而不等于1。同样地，0.3333……是以1/3为极限的变数而不等于1/3。人们常常把二者混同起来，其原因可以归结为对无穷小的特征——即趋于0而不等于0——认识得还不够充分，这里涉及潜无限和实无限的问题。

在哲学上，实无限和潜无限是有严格区分的。一般来说，实无限是完成了的无限，而潜无限是未完成的无限，即一个永无休止的无限过程。如中国老话所说：“一尺之棰，日取其半，万世不竭”(《庄子·天下》)其中“日取其半，万世不竭”就是一种潜无限，而这一潜无限的分割过程却是在“一尺之棰”中进行的，这一尺之棰就是实无限。需强调，实无限是相对于潜无限而言的，离开潜无限，实无限也就不存在了，只不过是单纯的有限而已。如，如果离开“日取其半，万世不竭”的潜无限，一尺之棰只有一段有限的长度，而不是实无限。

类似地，无限趋于某一极限的过程如0.9999……是潜无限，而它所趋近的那个极限1是实无限。如果离开0.9999……的潜无限，1仅仅是一个确定的有限数而不是实无限。一般地说，一个整数比在数轴上是一个确定的点，因而是有限；但当它作为某一无限趋近(潜无限)的极限的时候，它则成为一个实无限。实无限是潜无限和有限的对立统一。

实无限是一个辩证法的概念。一方面，实无限不能离开潜无限而孤立地存在，一旦孤立地存在便蜕化为单纯的有限。另一方面，实无限不等于潜无限，因为实无限具有有限性和确定性，而潜无限只是单纯的无限过程，不具有有限性和确定性。需要指出，由于数学家们对于辩证法概念掌握得不太好，这使他们把作为潜无限的0.9999……和0.3333……分别等同于它们各自的极限1和1/3，而把中间的差值即无穷小作为0而忽略掉了。为了更明显地揭示这一错误，我们对一个“证明”——证明无限循环小数等于一个整数比——进行分析。

求证：0.323232……(即以32为循环节的无限循环小数)为一整数比。

证明：

设：x=0.323232……=0.32+0.0032+0.000032+……

①

两边都乘以100得

100x=32+0.32+0.0032+0.000032+……

②

②―①得

100x―x=32，故99x=32，x=32/99

所以，0.323232……=32/99。证毕。

此证明的错误在于，由②―①得出100x―x=32。而正确的结果应是：

100x―x=32―δ (δ→0)

③

这是因为②和①的右边都是无限的相加过程，这使②―①所得的右边是一个无限的相减过程。在有限的情况下，由②―①得出：

100x―x=32―0.00……0032

其中0.00……0032是①右边的最后一个加项，为一有限数(小数点后的0为有限个)。在无限循环的情况下(即小数点后边的0趋于无限多个)，此加项趋于无穷小，故而得出③。不难看出，以上“证明”之所以由②―①得出100x―x=32，就在于把③中等号右边“32―δ(δ→0)”中的无穷小δ作为0而忽略掉了；这相当于把潜无限等同于实无限，这是一种概念上的混淆。

为了加以比较，我们不妨以正确的方式证明：0.9999……=1―δ(δ→0)。

设：x=0.999=0.9+0.09+0.009

①

两边都乘以10得

10x=9+0.9+0.09

②

②―①得

10x―x=9―0.009，故9x=9―0.009

所以，x=1―0.009/9

③

现把假设由x=0.999改为：x=0.999……，即把有限小数改为无限循环小数，相应地，③右边的0.009/9变为0.0…09/9(分子的小数点后的0有无限多个)，从而③变为：

x=1―0.0…09/9=1―δ (δ→0)

所以，0.999……=1―δ (δ→0)。证毕。

如果说0.323232……=32/99或0.333……=1/3的错误还不太明显，那么，0.999……=1的错误便昭然若揭了。为什么会有这样的差别？那是因为一个整数比如1/3具有双重性，它既是数轴上一个确定的点，又是一个无穷的计算过程即1÷3；这个无穷计算过程的结果就是无限循环小数0.333……，因而用等号将二者连接起来有一定的合理性，但却忽略了1/3的确定性和有限性与0.333……的不确定性和无限性之间的差异。1/3作为数轴上的一个确定点只是0.333……无穷过程的极限，而不是0.333……本身。与之对照，由于1只是一个有限数而不是一个无穷的计算过程，因而只具有有限性这一方面，而没有潜无限之另一方面，这便使0.999……=1的不妥之处暴露出来。总之，从理论上讲，0.333……=1/3正如0.999……=1都是不妥的，其错误的根源就是把一个无限趋近的过程等同于其极限，把潜无限等同于实无限。

既然无限循环小数不等于任何整数比a/b，而只是以某个整数比为其极限，那么整数比也就不能作为有理数的定义，而只是有理数的一部分，另一部分是无限循环小数。如果我们还要把有理数作为有限数和无限循环小数的并集，那么有限数的定义需要作相应的改变，即把有限数定义为整数比a/b，而整数和有限小数(即原来的有限数)只是它的子集。在此意义下，有限数的含义是它可精确地对应于数轴上的一个点，而不是以数轴上的一个点为其极限。相应地，有理数的含义是：它可精确地对应于数轴上的一个点，或者以数轴上的一个点为其极限。显然，无限不循环小数不满足这个定义。这样，虽然“有理数”和“无理数”在外延上与教科书仍然保持一致，但其内涵已经发生一定的变化。

也许有人会对此结论提出质疑：数学是以精确性而著称的，如果教科书和数学家们混淆了潜无限和实无限，为什么在人们的实践活动中没有导致明显的不良后果？对此，笔者的回答是：这涉及理论和实践的关系问题；正如数学史上关于数学基础的三次危机并未明显地影响应用数学的发展。无理数的发现导致第一次数学危机，贝克莱悖论导致第二次数学危机，罗素悖论导致第三次数学危机；其实这三次数学危机都涉及同一个哲学问题，那就是潜无限和实无限的关系问题。接下来，我们从理论和实践的关系上对此问题做进一步讨论。

四、理论的不确定性和现实的确定性之对立统一

从理论上讲，任何现实的测度都只是近似地准确，因而具有一定的不确定性。不过，当现实测度的近似性程度达到很高的时候，便在现实中把它看作精确的和确定的。这就是理论的不确定性和现实的确定性之对立统一。这种对立统一的重要性在于：现实通过对理论的变通而具有可行性，理论给现实以指导，使其精确性不断提高。理论的不确定性和现实的确定性之对立统一，属于辩证法的范畴，它是理论与实际相互促进和相互结合的哲学基础，对于解决“数学危机”问题是至关重要的。三次数学危机涉及无理数、微积分和无穷集合等概念，下面我们着重讨论前两者。

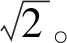
设y=x2,其导数为dy/dx，即dx2/dx，它表示当x增量Δx趋于0时增量比Δy/Δx的极限。函数的增量Δy=(x+Δx)2-x2=2xΔx+(Δx)2,两边同除以Δx便是所要的增量比即：Δy/Δx=2x+Δx。导数就是这个增量比当Δx趋于0时的极限，记为：

请注意，导数dy/dx中的dx是一无穷小而不是0，否则不能作除数。dx也就是当Δx→0时的Δx，因而此公式中的Δx也是一个无穷小而不是0。然而，此公式得出dy/dx=2x，显然是把公式中最后一个Δx作为0来对待的。这便使求导过程出现逻辑矛盾，即当Δx→0时，Δx既是0又不是0；更一般地说，无穷小既是0又不是0。

这个矛盾也被称为“贝克莱悖论”，因为它是由18世纪英国哲学家贝克莱(George Berkeley，1685-1753)首先提出的。当时微积分刚被牛顿提出不久，其论证不太严密，这使贝克莱十分不满。贝克莱指责牛顿说：“我所非议的不是您的结论，而是您的逻辑和方法……这些消失的量是什么呢？它们既不是有限，也不是无限小，又不是零，难道我们不能称它们为消失量的鬼魂吗？”[3]189-190

应该说，贝克莱对牛顿微积分理论的批评是中肯的。一方面，贝克莱指出其中的矛盾之处；另一方面，他没有否定该理论在实际应用上的正确性。如何在保留微积分的同时而消除“贝克莱悖论”呢？现在一般认为，数学家们经过近两百年的努力，“直到19世纪柯西才真正用极限的概念把它基本说清楚，而魏尔斯特拉斯最终用ε-δ的语言，彻底解决了这个困难，从而推动了近代分析的蓬勃发展。”[5]30然而，在笔者看来，用ε-δ语言表达的极限概念虽然对“贝克莱悖论”的解决有所促进，但说“彻底解决”有些言过其实。为说明这一点，我们把教科书中关于函数极限的ε-δ定义抄录如下：[注]同济大学数学教研室：《高等数学》上册(第四版)，高等教育出版社1996年版，第44页。邓东皋，尹小玲：《数学分析简明教程》第52页的表述是一样的，只是把“去心邻域”表示为“除x0点外”。华东师范大学数学系：《数学分析》上册(第三版)第44页的表述也是相同的，只是把“去心邻域”表示为“空心邻域”。

设函数f(x)在点x0的某一去心邻域内有定义，如果对于任意给定的正数ε(不论它多么小)，总存在正数δ，使得对于适合不等式0<│x―x0│<δ的一切x，对应的函数值f(x)都满足不等式│f(x)―A│<ε，那么常数A就叫做函数f(x)当x→x0时的极限，记作

limx→x0f(x)=A 或 f(x)→A(当x→x0)

在以上定义中，有三点需要特别注意。其一，函数的极限是常数而不是变数。其二，对于“去心邻域”这个概念，该教材加以解释：“定义中0<│x―x0│表示x≠x0，所以x→x0时f(x)有没有极限，与f(x)在x0是否有定义并无关系。”[6]44例如，对于f(x)=1/x这一函数，尽管在x=0处没有定义，但并不妨碍我们求得f(x)在0点的极限，即：

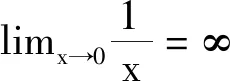
其三，该极限定义给出两种极限表达式，用“或”表示对二者可以自由选用，意味着二者是完全等价的。然而，需要指出，这是对实无限和潜无限的混淆。“或”的左边是关于实无限的，把极限等同于一个常数A；“或”的右边是关于潜无限的，它表示极限A所对应的无限趋近的过程，而不表示A本身。

正如我们在前边指出的，潜无限和实无限是不相等的。这种混淆的不良后果在函数f(x)=1/x上充分显示出来，即当x→0时，∞作为一个常数出现在等号的右边。然而，“无穷大(∞)不是数。”[6]53因此，“当x→0(x→∞)时为无穷大的函数f(x)，按函数极限定义来说，极限是不存在的。但为了便于叙述函数的这一性态，我们也说‘函数的极限是无穷大’。”[6]53这样一来，“贝克莱悖论”便以另一种形式出现了，即“无穷大既是数又不是数”，它不过是“无穷小既是0又不是0”的变形。可见，极限的ε-δ定义并没有把贝克莱悖论“彻底解决”。

请注意以上引文中的这句话：“按函数极限定义来说，极限是不存在的。”这意味着，严格地说，存在无极限的收敛，尽管无收敛的极限是不存在的；换言之，收敛和极限是不对称的。对于函数f(x)=1/x来说，当x→0时就是无极限的收敛；在几何图形表现为这样的曲线，它与数轴的y轴和x轴形成渐近线，无限地延伸下去但永不相交。如果说有极限的收敛是可望而不可及的，那么无极限的收敛就是不可望而不可及的。

进而言之，如果说，函数f(x)=1/x当x→0时的极限只是一种特例，那么，在极限的ε-δ定义中引入“去心邻域”却是普遍地不恰当的，无论x→x0时的x0是什么。因为x无限趋近x0即x→x0是潜无限，而作为其目标中心的极限x0是实无限，二者本来就是不相等的，即使不“去心”也是达不到的；因此“去心邻域”的引入不仅是“画蛇添足”，而且引起歧义。

具体地说，该定义引入“去心邻域”，言外之意，如果不把邻域的中心去掉，无限趋近的过程是可以达到其极限的。显然，这是对潜无限和实无限的混淆。其结果是：既然定义中只对自变量x向x0的趋近规定了“去心邻域”，而没有对函数f(x)向其极限A的趋近规定“去心邻域”，因此f(x)与A可以用“=”联结起来，即limx→x0f(x)=A。这里存在逻辑矛盾，即无限趋近的过程既可达到其极限而又不可达到其极限，这便为“贝克莱悖论”埋下伏笔。

贝克莱对牛顿的微积分理论提出批评，并非针对其结论而是针对其逻辑性的；同样地，我们以上对ε-δ极限定义的批评并非要否定limx→x0f(x)=A这个公式，而是要指出其表述上的逻辑不协调性。为了从根本上消除“贝克莱悖论”，我们需要借助辩证法的原理，即理论的不确定性和现实的确定性之对立统一。现在我们首先消除贝克莱指出的求导过程中的逻辑矛盾，然后对ε-δ极限定义加以改进。

还以前边曾讨论过的函数f(x)=x2的求导过程为例。推导过程的最后一步是

从理论上讲，当Δx→0时，Δx始终不是0，直到上面最后一步中Δx的最后一次出现；只是出于现实可测度性和确定性的考虑，我们把这最后一步中的无穷小Δx忽略掉了尽管它不是0。这里没有“无穷小既是0又不是0”的逻辑矛盾，只有把无穷小忽略不计的现实策略；这样，“贝克莱悖论”便不复存在了。

推而广之，ε-δ定义给出极限的两种不同表达，其中“f(x)→A(当x→x0)”表示极限的潜无限方面，“limx→x0f(x)=A”表示极限的实无限方面。换言之，前者表示趋向极限的无休止的过程，具有理论的不确定性；后者表示此过程所对应的确定目标即极限，具有现实的确定性。这两种表达式并不相等，但却是互补的；因此，这里没有把潜无限等同于实无限的逻辑矛盾。具体地说，在计算过程中，只取极限的潜无限方面，即“f(x)→A(当x→x0)”，这使无穷小可以做除数，以满足数学理论的严格要求；一旦无穷小不再出现在除数中，便取极限的实无限方面，即“limx→x0f(x)=A”，以满足现实的确定性要求。这是理论的不确定性和现实的确定性之对立统一，而不是逻辑矛盾。

然而，这两种表达式在极限的ε-δ定义都出现，用“或”字表示可以自由选用，二者是完全等价的，这便蕴涵逻辑矛盾。与之不同，在上面的阐释中，这两种表达之间的关系不是形式逻辑的简单同一性，而是辩证法的对立统一性，即理论的不确定性和现实确定性的对立统一。这样，“贝克莱悖论”及其各种变形便得以消除。

此外还需强调，在我们的表述中，x→x0只表示x趋近于x0而永远不等于x0，它和x0之间是潜无限和实无限的关系，因此无需引入“去心邻域”这一概念。相应地，函数f(x)=1/x当x→x0时只是趋近于∞而永远不等于∞。这是理论的不确定性，但是，出于现实确定性的考虑，我们可以把“无限收敛”也看作一种特殊的极限。对于f(x)=1/x来说，其几何意义是指曲线与数轴无限靠近，当其靠近的差距小到现实中可以忽略的地步，我们便可认为二者是重合的。一般而言，函数f(x)当x→x0时收敛到无穷小的区域，从现实确定性的角度，可以把这无穷小区域看作此函数当x→x0时的极限。

这意味着，从现实的确定性和可行性的角度出发，函数的极限不局限于常数，也可以是无穷小或无穷大这样的变数。这样处理有两个显著的优点：其一是，∞一旦出现在极限等式的右边也可顺理成章地看作一个数；另一是，无理数作为收敛于无穷小区间的变数也可以作为极限。这后一点对于下一节关于“极限存在准则”的讨论尤为重要。

综上所述，微积分比起初等数学的高明之处就在于超越单纯形式逻辑的思考，而进入理论严格性与现实可行性之间的变通，从而把潜无限和实无限统一起来而不是等同起来。在此意义上，正如恩格斯所说，微积分的确含有辩证法的因素，“本质上不外是辩证法在数学方面的运用”。辩证法不是对形式逻辑的否定，而是对形式逻辑的超越。正因为此，在微积分理论中并不包含也不允许出现逻辑矛盾。

五、关于柯西定义和戴德金分划

前述表明，极限的ε-δ定义引入“去心邻域”，从理论严格性上讲是多余的。不过，从现实可行性上讲，这一概念倒是给人一种启示，即一个变量无限趋近的目标之性质并非单一的，可以是实的，也可以是空的。但是，事实上现行教科书却把无限趋近的极限只看作实的，即看作一个点即常数，因为任何极限值都在实数的范围内，“任一实数都对应数轴上唯一的一点；反之，数轴上的每一点也都唯一地代表一个实数。于是，实数集R与数轴上的点有着一一对应关系。”[4]3现在看来，这种说法有先入为主的成分。既然极限可以是“空的”，为什么这“空隙”一定是点而不是无穷小的区间，一定是常数而不是变数？

从上面的分析中我们看到，无理数的特征就是不可测度，它在数轴上不是一个确定的点，而是一个无穷小的区间。考虑到无理数也可作为极限，我们有必要把极限的范围从点扩展到无穷小区间，从常数扩展到变数。相反，把极限的范围局限于点或常数，把实数和数轴之间的关系看作数与点的一一对应，这实际上是用有理数的观念来看待无理数。其结果是使贝克莱悖论不可能被“彻底解决”，并使微积分理论至今仍然存在一些含混不清甚至自相矛盾的说法，包括著名的“柯西极限存在准则”和“戴德金连续性准则”。

柯西曾把无理数定义为：无理数是有理数序列的极限。这个说法虽然极富启发性，但在他的理论中是难以自圆其说的；因为无理数作为无限不循环小数是不可度量的，并不对应某个确定的点或常数，而柯西所说的“极限”却只限于点或常数。柯西关于无理数的这一定义蕴涵于“柯西极限存在准则”(也叫做“柯西收敛准则”)之中，此准则表述如下：[4]38

数列{an}收敛的充要条件是：对任给的ε>0，存在正整数N，使得当n，m>N时有：│an―am│<ε。

柯西极限存在准则的条件称为“柯西条件”，其直观意义是：收敛数列{an}各项的值愈到后面，彼此愈是接近，以至充分靠后的任何两项an和am之差的绝对值小于预先给定的任意小正数ε；其在数轴上的表现是，收敛数列的各项越到后面越是拥挤在一起。

显然，无理数作为有理数的无穷序列是满足柯西条件的，因为随着小数位数的增加，越往后两个数之间的差距就越小。根据此准则，一个无理数所对应的有理数序列是收敛的，收敛意味着有极限，那个极限就是该无理数。在此意义上，我们可以把无理数定义为“有理数序列的极限”。但是，柯西却额外地增加了一层意思，那就是：序列(或函数)有极限则意味着收敛于某一常数或数轴上的某一点，相应地，无理数是一常数并对应于数轴上的一个确定的点。

请注意，与通常的ε―N数列极限定义相比，[注]数列的ε―N极限定义是：若对任给的正数ε，总存在正整数N，使得当n>N时有│an―a│<ε,则称数列{an}收敛于a，定数a称为数列{an}的极限。(参阅华东师范大学数学系：《数学分析》上册，第23页)柯西极限存在准则有着实质性的区别，即把关于an与a充分靠近的关系换成了an与am充分靠近的关系。这就是说，前者借助于数列以外的数a即那个极限，而后者只需根据数列本身的特征，即充分靠后的任何两项an和am之间的差距；前者是用数列“有极限”来定义数列“收敛”，而后者是用数列“收敛”来定义数列“有极限”。

从数轴上看，前者是从a的邻域向其中心点即极限a的靠拢来定义数列的收敛，后者是从数列各项的靠拢来定义数列收敛并有极限。显然，后者比前者断定的东西要少而前者断定的东西较多，其差别在于是否把收敛的极限定义为某个常数。柯西试图从后者直达前者，即从满足柯西条件的序列收敛于某一极限的断言直达关于此极限是一常数的断言，这便需要给以证明。对此，柯西本人并未给出令人信服的论证，于是，对“柯西极限存在准则”的证明成为其他数学家的艰巨任务。

然而，在笔者看来，数学家们对柯西极限存在准则的证明是误入歧途的。如果把数列收敛的极限不限于常数或数轴上的一个点，也可以是一变数，其变域是数轴上的一个无穷小区间，那么柯西极限存在准则是非常直观的，不需要加以进一步的证明，而且ε―N数列极限定义可以作为特例从柯西极限存在准则推导出来。令人遗憾的是，由于数学家们在这个问题上钻了牛角尖，认定极限只能是常数或数轴上的一个点，那就不得不勉为其难，承担起证明柯西极限存在准则的重任。

这个任务的难点在于证明可以作为极限的无理数也是一个常数。应该说，这个任务是不可能完成的，因为无理数在其本质上就不是一个常数或数轴上的一个点。这便使得数学家们为此所做的“证明”不仅迂回繁琐，而且难免出现逻辑错误。对于柯西极限存在准则，数学家们给出多种“等价”的证明，其中比较“直观”的一种是借助于“戴德金分划”。

戴德金(J.Dedekind，1831—1916)尤其关心实数的连续性，这便涉及无理数的定义问题。其实，戴德金是以直线的连续性作为实数连续性的模型，如果实数与直线完全重合，那便表明实数是连续的。戴德金在其力作《连续性与无理数》中写道：关于实数的连续性，“经过长期徒劳的思考，我终于发现它的实质是很平凡的。直线上的一点，把直线分成左右两部分。连续性的本质就在于返回去：把直线分割成左右两部分，必有唯一的分点。”[5]9

这就是说，把直线分割成两部分的那个分点存在于实数中，并且是“唯一的”。这样，实数与直线上的分点便是一一对应的，因此，实数便具有了直线的连续性。显然，在戴德金的心目中，包含于实数中的无理数也具有唯一性，对应于直线上的一个确定的点。可以说，除了把无理数看作直线上的一点不够直观，把实数的连续性挂靠在直线的连续性上，这是很自然也很直观的；正如戴德金自己所说，这一思想是“很平凡的”。

以上便给出实数连续性的实质，其道理不仅是“平凡的”，而且是直观的，甚至是不证自明的。然而，数学家们却有一个心结，总觉得让无理数对应于有理数之间的“空隙”不太实在，还想让无理数对应于数轴上一个确定的点，这样便有必要直接地用有理数来定义无理数，而不能只用有理数的反面即“空隙”来定义无理数。“用有理数构造新数的方法很多,如戴德金的分划说,康托尔的基本列说,区间套说等等。”[4]290数学家们的艰苦努力就在于“用有理数构造新数”，所谓“新数”就是无理数。

对于“戴德金分划”，现行教科书还作出这样的解释：“数集无空隙，或更通俗地说：如果将实数集看作一条直线，并用一把没有厚度的理想的刀来砍它，那么不论砍在哪里，总要碰着直线上的一点。”[4]294请注意，戴德金分划的那个分点是“没有厚度的”，因而是一个欧几里得几何学的点，而不是微积分中的无穷小，是一个常数而不是一个变数。用这样的点构造的实数使得“数集无空隙”，从而成为连续的。

不难看出，这种思维潜伏着一个矛盾，那就是让微积分理论的核心概念“无穷小”，退回到初等数学的没有长、宽、高的欧几里得点。数学家们用有理数的“点”来定义无理数，这一企图就预示着这种倒退，无异于缘木求鱼、南辕北辙，在大方向上是误入歧途的。关于“戴德金连续性准则”，笔者不打算亦步亦趋地分析那些“证明”的各个步骤，而是尽可能直截了当地指出其中的关键性错误。

“戴德金连续性准则”可以这样来表述：如果一个有大小顺序的稠密的数系S，对它的任何一个分划，都有S中唯一的数存在，它不小于下类中的每个数，也不大于上类中的每一个数，那么称S系是连续的。[5]9

需加说明，一个戴德金分划把数系S分为两个部分即下类和上类，下类中的每一个数都小于上类中的每一个数，并且这两个类的并集等于S，这就是所谓“不空、不漏、不乱”的戴德金分划的三个性质。戴德金连续性准则给出的前提条件是“对S的任何一个分划，都有S中唯一的数存在”，由于下类和上类合起来是“不漏”的，因此，这个作为分点并且存在于S中的数要么是下类的上端，要么是上类的下端，而不会漏在下类和上类之间的空隙之中。这也就是说，对S的任何分划的分点都不会落在S的外边，所以，S是没有空隙的，因而是连续的。

这里的问题是：对S的任何分点都不会落在S的外边就一定表明S是连续的吗？为了给出肯定的回答，必须假定S的所有分点的集合是连续的。那么，问题转变为：如何表明“S的所有分点的集合是连续的”？回答只能是：数轴上的每一点都可成为S的分点，数轴是连续的，所以S的所有分点的集合是连续的。由此可见，戴德金连续性准则是以直线的连续性为模型的，如果离开这一点，该准则便成为无源之水、无本之木。

为了使这一结论更加明晰，我们不妨让分划的分点只包括有理数(有理数满足数系S的稠密性要求)，而不包括无理数；毫无疑问，全部分点都将落入有理数的范围。根据戴德金连续性准则，那将得出结论，有理数是连续的。然而，有理数不连续，这说明戴德金连续性准则的表述是不完备的。

对此，可能有人会反驳说，为什么可以把无理数从分划的分点中排除呢？笔者将反问：为什么不可以呢？有理数系也具有稠密性，并且用任何有理数作为分点也可满足关于有理数的“不空、不漏、不乱”的要求，除此之外，戴德金连续性准则对“分划”并未做其他限定。况且从直观上讲，有理数的稠密性意味着，在任何两个不同的有理数之间都有无穷多的有理数存在，而无论这两个有理数在数轴上的距离多么小，难道这还不连续吗？

可以看出，为要反驳以上关于有理数之连续性的“证明”，无法只凭戴德金连续性准则来进行，必须在此准则之外寻找根据，其根据归根到底就是作为数轴的直线的连续性。这一“反驳”大致是这样的：既然有理数没能布满直线，还留下许许多多的“空隙”，所以，有理数是不连续的；我们把这些“空隙”叫做无理数，有理数和无理数合起来便能布满直线，所以实数是连续的。分划直线的分点可以是直线上的任何一个点，当然包括无理数。然而，以上关于有理数之连续性的“证明”则把无理数从分划的分点中排除掉，因而是不恰当的。

须指出，此“反驳”有一逻辑错误即偷换概念：先把无理数作为直线上的有理数点之间的空隙，后把这些空隙作为直线上的点，即戴德金分划的“分点”，从而证明无理数也是直线上的一个点，以此把实数与直线上的点一一对应起来。这一逻辑错误潜藏于“戴德金连续性准则”的证明过程中。

以上从总体上表明“戴德金连续性准则”的不恰当性。接下来，我们将对此准则的证明过程加以分析，指出其中的一些逻辑错误，其关键之点是对数学归纳法的误用。下面，我们对一部有代表性的教材中的证明过程进行分析。[注]参见邓东皋、尹小玲：《数学分析简明教程》上册，第11-12页。该书的一些错误并非独有，而是普遍存在于大部分教科书中。相对而言，该书阐述的较为清晰，故以该书的证明过程作为分析的对象。

证明：设A│B是实数系R的任何一个分划。我们要证明存在唯一的实数r∈R，使得对任意a∈A有a≤r，对于任意b∈B有r≤b。

首先看全体整数，由A不空知有整数属于A。若任意整数c0∈A，有c0+1∈A，则B是空集；既然分划A│B规定B不是空集，那么存在整数c0，使得c0∈A，而c0+1∈B。其次考虑：

c0.0，c0.1，c0.2，…，c0.9

这时必存在c1是0，1，…，9中的某数，使得c0.c1∈A, c0.(c1+1)∈B,(若c1等于9，则c0.(c1+1)=(c0+1).0)。如此继续下去，在确定了c0.c1…cn之后考虑

c0.c1…cn0，c0.c1…cn1，…，c0.c1…cn9

由此确定cn+1,使得c0.c1…cncn+1∈A，c0.c1…cn(cn+1+1)∈B，如此便得到实数

r=c0.c1c2…cn…

(对教科书的有关证明引用到此)这个r就是实数系R中的戴德金分划A│B的分点，其小数位数n可以是无穷大，这便把无理数包含在内。不过，无论n多么大，我们总可以把分划A和B的那个数值cn确定下来，使得c0.c1…cn∈A，而c0.c1…(cn+1)∈B。

对于以上论证，我们可以看到，其中包含着对数学归纳法的使用，归纳过程如下：首先，在整数上可以确定把实数集A和B分划开来的数值c0。其次，如果在第n位小数可以确定把A和B分划开来的数值，那么在第n+1位上也可以；否则通过十进制进位的递归，使得所有数都属于A类而使B为空类，违反戴德金分划关于“不空”的规定。这样，由数学归纳法可得：在任何小数位数n上，都可以确定分划A和B的分点，其分点包括小数位数n为无穷大的无理数。

通过这一数学归纳法的使用，把有理数的分点性质推移到无理数上，这个性质就是：一个数对应着数轴上的一个点，这个点是可用十进制刻度来确定的，而无论刻度单位多么小，甚至是无穷小。这就是数学家们想要的结论，即实数与数轴上的点是一一对应的，相应地，它们的连续性是从点到点的连续性。这样，无理数便用有理数构造出来了。

然而，笔者要指出，以上对数学归纳法的使用是不适当的，因为它误解了数学归纳法的功能。数学归纳法的功能是对同类对象的性质作出概括，如：1+1是自然数，如果n+1是自然数，那么(n+1)+1也是自然数，所以，任何自然数加1之后仍为自然数。这是对同类对象即自然数的“加1”性质作出概括，因而是对数学归纳法的正确使用。但是，由数学归纳法得不出无穷大∞加1之后是自然数，尽管n+1+1+……的极限是∞；这是因为∞与自然数不是同一类对象，自然数是常数而∞则是变数。类似地，通过以上数学归纳法只能得出“任何有理数分点对应于十进制刻度上的某一点”，而不能把此结论推广到无理数上，因为无理数与有理数不是同一类对象，其本质区别就在于是否在数轴上可以度量。

至此，我们揭示了“柯西极限存在准则”和“戴德金连续性准则”的含混和不当之处，其症结在于把无理数看作数轴上的一个点而不是一个无穷小区间，进而把无理数看作常数而不是变数。既然“戴德金分划”并未成功地表明无理数是一常数或数轴上的一个点，那么我们不妨把数列或函数收敛的极限从常数或点扩展到变数或无穷小区间。这样做的显著优点是，“柯西极限存在准则”成为公理而无需加以证明，相应地，戴德金连续性准则及其各种等价“原理”成为多余的；[注]事实上，包括同济大学《高等数学》在内的许多教材把“戴德金连续性准则”及其等价“原理”的证明省略了，其多余性由此可见一斑。这不仅使微积分的理论基础更加简洁明了，而且使“贝克莱悖论”得以彻底的清除。

六、“芝诺佯谬”与辩证法的运动论题

前面提到，辩证法的运动论题早在古希腊时期就以“芝诺佯谬”的形式被间接地提出。芝诺佯谬有多种表述，现只以“飞矢不动”作为讨论的案例。“飞矢不动”所呈现的疑难问题是：一支刚射出的箭在到达靶心之前必须经过箭头与靶心之间的中点；同理，必须经过中点的中点，以此类推。所以，一支射出的箭在到达靶心之前需要经过无数多个中点，以致那支箭无法到达任何一点，只能留在原地纹丝不动。[注]亚里士多德在其《物理学》中较为详细地介绍了四种形式的芝诺佯谬(见《物理学》，徐开来译，中国人民大学出版社，2003年，第180-181页)。这里的表述是将其中第一个即“运动不存在”与第三个即“飞矢不动”合并起来。

“飞矢不动”是纯理论分析的结果，它与事实上的“飞矢可动”形成鲜明的反差。据说当时一位古希腊的智者听到芝诺佯谬之后，从他常坐于其中的木桶里跳了出来，在地上来回走动，以此来反驳芝诺佯谬。其实这是答非所问，因为芝诺本人也不会否认事实上的“飞矢可动”。正因为此，他通过理论分析所得到的“飞矢不动”才具有震撼力，逼迫理论家们不得不加以解决。面对“飞矢可动”的铁一般的事实，“飞矢不动”的理论分析一定存在某种错误。错误在哪里，如何解决？这是摆在人们面前的问题。

通过前面对实数和直线的连续性的讨论，我们已经得出一个重要的结论即：实数的连续性是由有理数和无理数共同构成的，反映在数轴上，有理数的点和无理数的无穷小区间即“空隙”共同构成数轴的连续性。相应地，一支箭从出发点到靶心的轨迹是一条连续的曲线，上面并非只有无数多个“中点”，而在诸多中点之间还有许多无穷小的区间。诚然，无数多个没有长宽高的点加在一起还是一个没有长宽高的点，正如无数多个0相加等于0；但是，无数多个无穷小区间加在一起并不等于0，而可成为一段有确定长度的线。这正是微积分的基本原理，即把一线段微分到无穷小，再把无数多个无穷小累积起来，就得到那条线段的精确长度及其相应的面积。

得出“飞矢不动”的理论分析的错误之处在于，把箭的运动轨迹仅仅看作无数多个“中点”的累积，而忽略了其中的无穷小区间；正如数学家们只看到数轴上稠密分布的无数个点，而没有看到其中稠密分布的无穷小区间。正因为此，数学家们对于芝诺佯谬显得束手无策。当然，数学家们可以通过微积分计算来解释芝诺佯谬，但那并不能从根本上解决问题。正如贝克莱所说，那只是微积分计算结果的实际正确性，其理论本身仍然潜伏着逻辑矛盾，并以“贝克莱悖论”的方式呈现出来。

对于芝诺佯谬的直截了当的解决就是承认数轴的连续性是由有理数的点和无理数的无穷小区间共同构成的，不妨称之为数轴或实数的“点域二象性”；这种点域二象性体现了潜无限和实无限的对立统一。具体地说，数轴上的每一个有理数点可以作为极限而对应于向它无限趋近的潜无限过程，即无限循环小数；每一个无理数通过不断展开的潜无限过程而对应于一个作为极限的无穷小区间。数轴是一种几何图像，它的点域二象性直接反映了空间的基本性质；数轴也可表示时间，其点域二象性也反映了时间的基本性质。

在现代物理学中，时间和空间同为四维空间的要素，因此也可说，点域二象性是时空量子的属性，对应于物理量子的波粒二象性。物理量子是经验对象，其波粒二象性需要通过实验加以验证；与之不同，时空量子不是经验对象，而是先验对象，正如时间和空间属于先验范畴(这是康德哲学的基本原理之一，康德称之为“先验直观”)，对时空量子的点域二象性只需通过逻辑和数学的分析便可确认。诚然，逻辑、数学与物理学之间具有某种对应关系，时空量子的点域二象性与物理量子的波粒二象性之间也具有某种对应关系。在这个意义上，我们也可把物理量子的波粒二象性看作时空量子的点域二象性的经验印证，二者都是间断性和连续性的对立统一。

最后，我们再回到辩证法的运动论题——运动在同一时刻既在一个地点又不在一个地点——的正当性上。我们在前面第二节根据微积分的导数概念即dy/dx得出结论：运动的瞬时速度不为0，意味着运动是同一瞬时在不同的空间点——瞬时速度的起点和终点——之间“跳跃”，这才使运动成为可能，从而克服“飞矢不动”的芝诺佯谬。在这个意义上，辩证法的运动论题是成立的；事实上，黑格尔在很大程度上是为解决芝诺佯谬而提出这一论题的。然而，这种表述似乎违反形式逻辑，相当于同时肯定A和非A。

笔者承认，这种形式的辩证法论题是粗糙的，容易引起误会，需要加以改进。现在我们根据无理数的无穷小区间性质，对辩证法论题的矛盾形式予以转化，以无矛盾的形式表述为：运动是在同一瞬时经过同一地点，瞬时和地点都是无穷小量而不是0。具体地说，原来的辩证法论题中所说的在同一瞬时被“跳跃”的那两个空间点，其实是在同一个无穷小区间之内的，因而是同一个地点而不是两个不同的地点。由无穷小量的累积可以成为一个有限数，所以，作为无穷小区间的瞬时和地点累积起来便可形成运动。这正是微积分数学的基本原理，也是芝诺佯谬得以解决的关键所在。

最后强调两点：其一，辩证法不是对形式逻辑的排斥，而是对形式逻辑的超越；相应地，恰当的辩证论题并不违反形式逻辑，而是在遵守形式逻辑的前提下蕴涵着更为丰富的内容。其二，数学基础的问题往往涉及潜无限与实无限的关系问题，这与其说是数学问题，不如说是哲学问题。正因为此，数学家们在此问题上的错误并不直接影响数学在实际应用上的正确性，但这并不表明其理论是完美无缺的。有趣的是，历史上的“三次数学危机”都是由哲学家发起的；也许，解铃还须系铃人吧。