UUV协同导航下MEMS陀螺仪协同标定

2019-07-16 06:16王秋滢

水下无人系统学报 2019年3期

王秋滢,尹娟

(哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨,150001)

0 引言

协同导航是指通过集群航行器之间导航信息的共享,使单航行器的导航误差得到校正的导航方式。在协同导航中,只需要给少量航行器配备高精度传感器,即可达到较好的导航精度。因此,协同导航不仅可以提高系统整体的导航性能,并且大大节约了成本[1],已广泛应用于无人水下航行器(unmanned undersea vehicle,UUV)集群中。

由于在水下无法有效获取高精度的全球定位系统(global positioning system,GPS)卫星信号进行导航定位,惯性导航、多普勒测速仪(Doppler velocity log,DVL)、长基线导航与航位推算被广泛使用于UUV的导航[2]。目前,航位推算是最常用的低成本导航解决方案,是指在已知初始位置的情况下,利用姿态传感器提供的航向信息以及DVL提供的速度信息对UUV的位置信息进行递推计算[2-6]。三轴地磁传感器与两轴微机电(microelectromechanical system,MEMS)陀螺仪组合姿态传感器具有功耗低、成本少、自主性强等优点,已经越来越多地应用于从UUV导航中。

由于航位推算的误差受导航传感器精度影响较大,当导航传感器精度不高时,往往需要对航位推算的误差及时校正。协同导航是最常使用的UUV航位推算误差校正方法。目前最主要的UUV协同导航方式为单领航艇主从式协同导航,在此方式中存在单个配备高精度导航系统的主UUV,多个配备低精度导航系统的从 UUV。从UUV利用主UUV发送的自身高精度导航信息以及主从UUV的相对距离对从UUV自身导航误差进行校正。

单领航艇主从式 UUV协同导航主要依赖UUV间的水声通信,如果水声通信中断,协同导航将不可用。由于MEMS陀螺仪精度较差,陀螺漂移大[7],严重制约了从UUV自身导航精度,此时若从 UUV上浮接受 GPS信号校正自身误差,则增加了从UUV能量消耗,减少了从UUV工作时间。因此,必须对MEMS陀螺仪的陀螺漂移进行辨识补偿,进而提高从UUV的导航精度,以达到在水声通信短时失效时,从 UUV导航精度仍能满足自身需求的目的。

目前,对于协同标定方面研究较少,文献[8]对协同导航下的 MEMS陀螺仪漂移标定进行了研究,但文献中仅对单轴陀螺进行标定,并且没有对协同标定路径设计进行分析。

针对上述问题,文中利用基于扩展卡尔曼滤波(extended Kalman filter,EKF)的协同导航结果作为标定观测量,在协同导航正常运行时在线解算出两轴 MEMS陀螺的陀螺漂移,提高从 UUV自身导航精度,以达到在协同导航短时失效时,从 UUV导航精度能够满足自身需求的目的。通过可观测性分析,确定协同标定的路径设计原则,并根据该原则设计 3组协同标定路径,通过滤波算法在线标定 MEMS陀螺仪的陀螺漂移并补偿。仿真结果验证了该方法可以快速有效地解算MEMS陀螺漂移,从而提高从UUV自身导航精度。

1 UUV集群协同标定模型及算法

1.1 UUV集群协同导航模型及算法

1.1.1 协同导航模型

UUV的运动可分为相对独立的水平面运动和垂直面运动,因为深度可由压力传感器直接测得,因此 UUV导航定位问题的研究可由三维空间转化至二维平面内。最常解决二维平面内导航定位问题的导航方式为航位推算[9]。在已知初始位置的情况下,利用三轴地磁传感器与两轴微机电 MEMS陀螺仪组合姿态传感器提供的载体航向信息以及 DVL等速度传感器提供的载体速度信息对载体的位置信息进行递推计算,进而实现水下航行器的导航定位。

地磁传感器三轴分别指向东北天,MEMS陀螺仪两轴分别指向载体的ox、oz轴。地磁传感器无法独立解算3个姿态角,需要已知1个姿态角才能解算另外2个姿态角[10]。因此,文中由两轴陀螺仪解算航向角提供给三轴地磁传感器解算横滚角和俯仰角,地磁传感器解算的横滚角与俯仰角再提供给陀螺仪解算下一时刻的航向角。

将 UUV的运动视为点运动体,即其运动轨迹可在东北向坐标系下进行描述。若已知 UUV初始时刻的位置 (px,1,py,1),则k时刻 UUV的位置可通过航位推算模型表示为

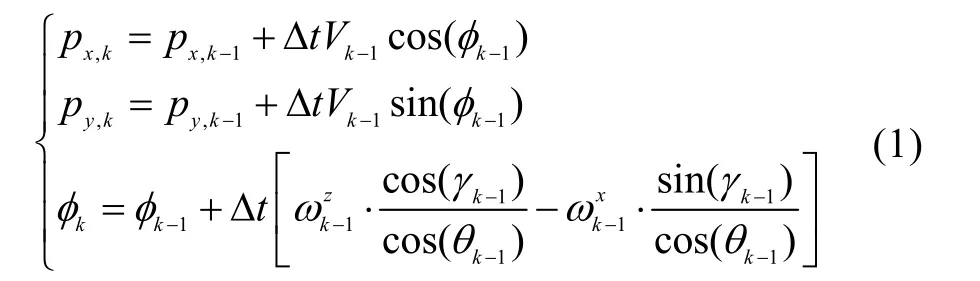
式中:Δt为采样时间间隔;Vk-1为 DVL测量的k-1时刻的UUV速度信息;φk,φk-1分别为k,k- 1时刻 UUV 的航向角信息;γk-1为k-1时刻UUV 的横滚角信息;θk-1为k-1时刻 UUV 的俯仰角信息;为z轴MEMS陀螺仪测量的k-1时刻航向角角速度信息;为z轴MEMS陀螺仪测量的k-1时刻航向角角速度信息。

航位推算模型可简单描述成

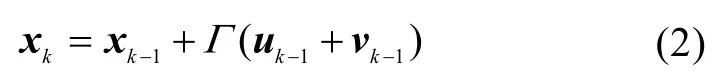
系统噪声协方差矩阵

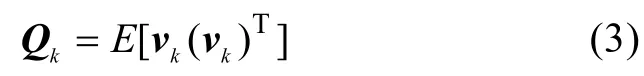
虽然航位推算应用简单、成本低廉,但是航位推算误差会随时间累积,导航效果取决于传感器的量测精度。配备低精度传感器的从 UUV由于传感器精度有限,导致航位推算精度较低,航位推算误差的时间累积性比较明显[11-12]。为抑制航位推算误差的不断积累,考虑以主、从UUV相对距离为观测量,通过协同导航算法,修正从UUV的位置误差和航向角误差,再将修正后的航向角提供给地磁传感器解算横滚角和俯仰角。

根据k时刻接收到的主 UUV参考位置信息以及从 UUV自身位置状态得到相应的距离观测方程。

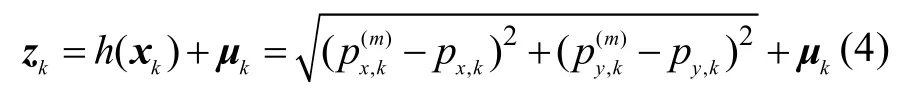
1.1.2 协同导航算法

由于协同导航系统的非线性特性,采用 EKF进行协同导航算法设计。根据上一节的协同导航模型,可得系统的滤波方程

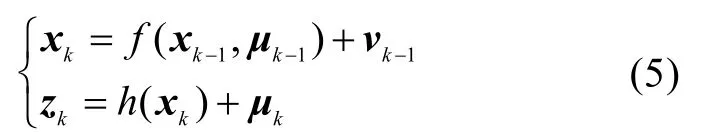
从UUV在k时刻的状态估计值

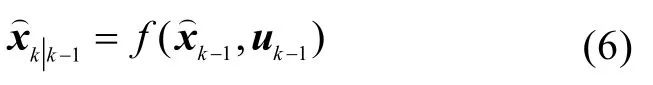
系统一步预测协方差为

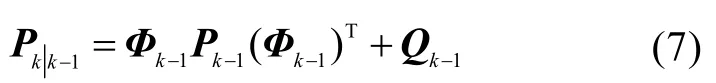
式中,Φk-1为状态转移矩阵,且

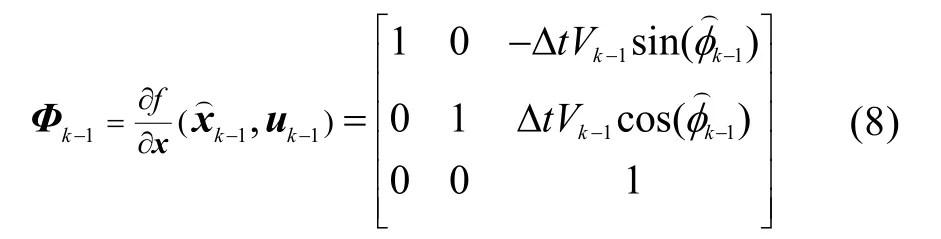
滤波增益为

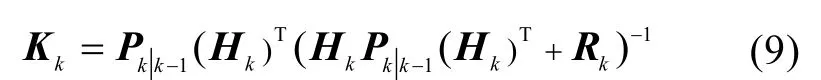
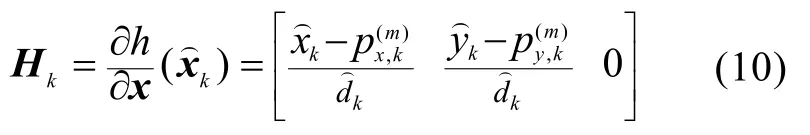
状态更新为

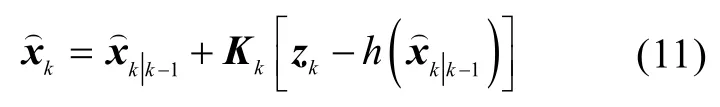
协方差更新为

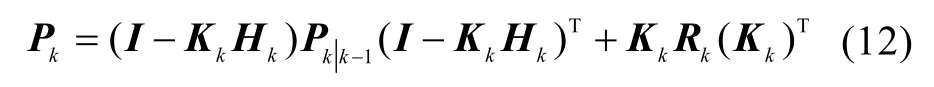
因此,只需给出从 UUV的初始状态量和初始化滤波方差,就可根据式(6)～式(12)递推估计从UUV每一时刻的位姿信息[13]。

1.2 在线标定模型及算法

1.2.1 在线标定模型

标定是一种针对 MEMS陀螺仪的有效误差补偿方法。传统的离线标定工作量太大并且需要巨大的成本投入,因此在线标定是减小MEMS陀螺仪陀螺漂移的首要选择。文中借助协同导航的结果,以协同导航校正后的航向角与未经校正的航向角差值以及地磁传感器输出的俯仰角与陀螺解算的俯仰角差值为观测量,通过滤波算法对两轴MEMS陀螺仪的陀螺漂移进行在线解算。

陀螺漂移是 MEMS陀螺仪最主要的确定性误差,其是惯性传感器输入为零时的输出。MEMS陀螺的陀螺漂移也称作零位漂移,单位常用(°)/h表示,陀螺漂移常记作ε。在水声通信短时失效时,陀螺漂移可认为是常值误差。

通过两轴 MEMS陀螺仪可解算航向角与俯仰角

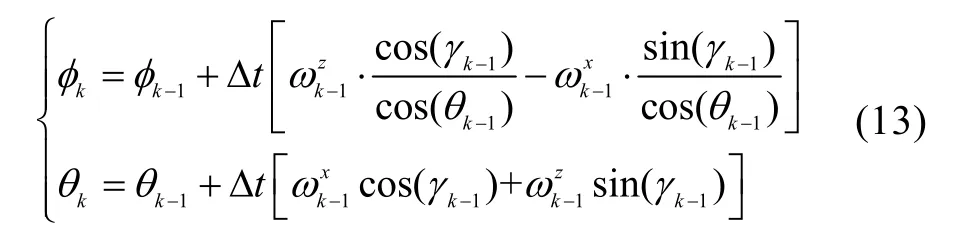
MEMS陀螺仪在线标定状态模型为

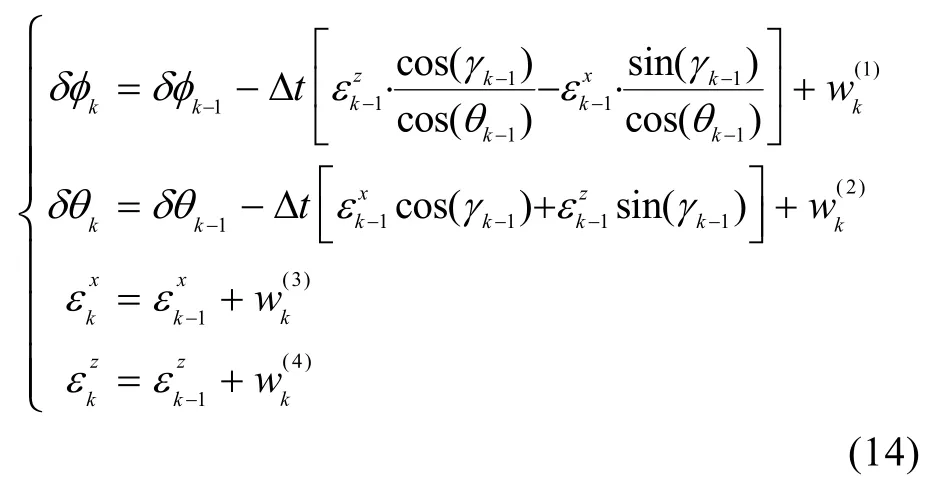
在线标定模型可简单描述成

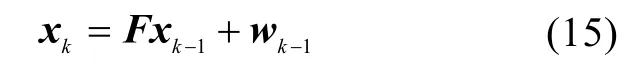
在线标定观测方程为

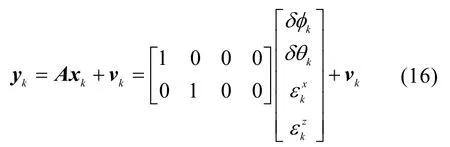
式中,vk为观测噪声矩阵。

1.2.2 在线标定算法

从UUV的MEMS陀螺仪在线标定模型为线性模型,文中选择卡尔曼滤波(Kalman filter,KF)算法进行解算。根据上一节的在线标定模型,可以得到系统的滤波方程为

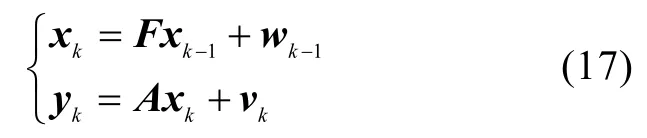
状态一步估计为

一步预测协方差阵为

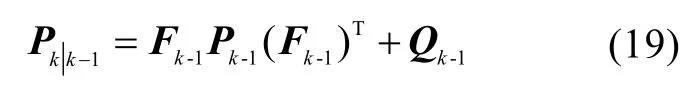
滤波增益矩阵为

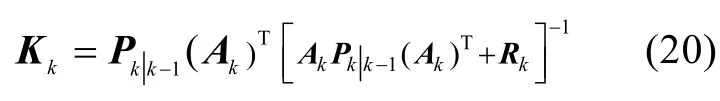
状态更新为

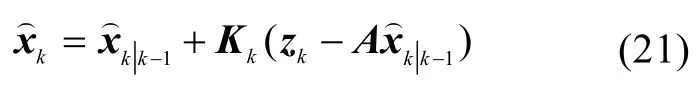
协方差矩阵更新为

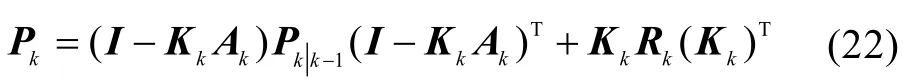
与EKF相同,只需给出初始状态量和初始化滤波方差,就能够递推估计每一时刻的状态量。

2 协同标定可观测性分析及路径设计

卡尔曼最早提出可观测性的概念:在一个线性系统中,若系统的观测信息唯一地确定系统所有状态量,则称该系统是可观测的。系统的可观测性反映了观测信息对于系统状态信息的解算能力。对于UUV协同标定来说,观测信息有限、观测能力较弱,因此,在协同标定之前有必要对系统的可观测性进行分析,明确系统的可观测条件,设计协同标定路径。

以如下所示的线性时变离散系统为例,说明系统可观测条件。

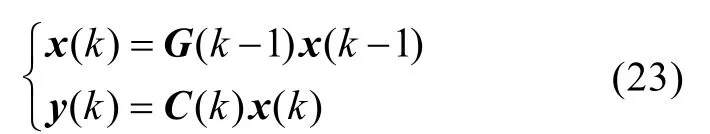
式中:x(k)为n维状态向量;y(k)为m维输出向量。

对于式(23)所示的线性时变离散系统完全可观测的充分必要条件为

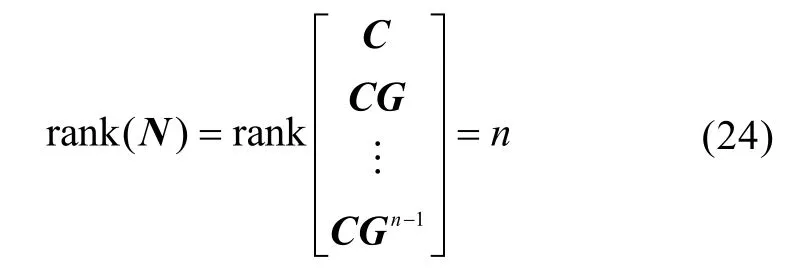
式中,N为系统的可观测性矩阵。

协同导航观测信息是一维距离量测量,因此至少需要进行3次观测才能获得系统的三维状态量唯一解。当进行3次距离观测时的系统可观测矩阵为

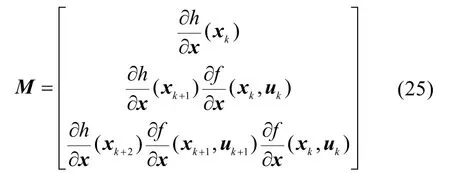
已知k、k+1、k+2时刻主UUV的位置为和以及主从UUV之间的距离观测量和则系统可观测矩阵进一步表示为

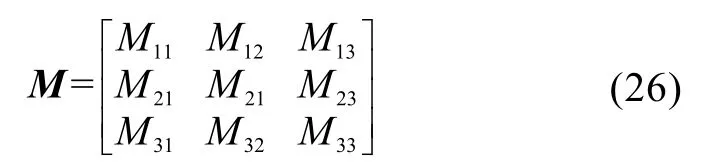
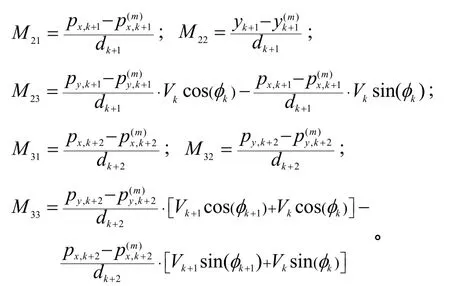
由于第 3列的第 1个元素为0,故从可观测矩阵可得:当第 1列或第 2列为 0时,即相邻 3个量测时刻主从 UUV的x轴或者y轴坐标是相同的,系统不可观测;或当第 1列或第 2列线性相关时,矩阵不满秩,即

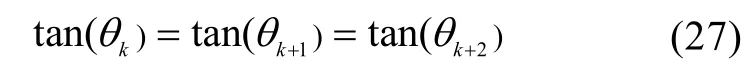
式中,θk为k时刻距离观测方位角。

从UUV的MEMS陀螺仪在线标定模型可以看出,当UUV的俯仰角与横滚角均为小量时,航向角误差可近似看做z轴MEMS陀螺仪漂移的累积,俯仰角误差可近似看做x轴MEMS陀螺仪漂移的累积,即

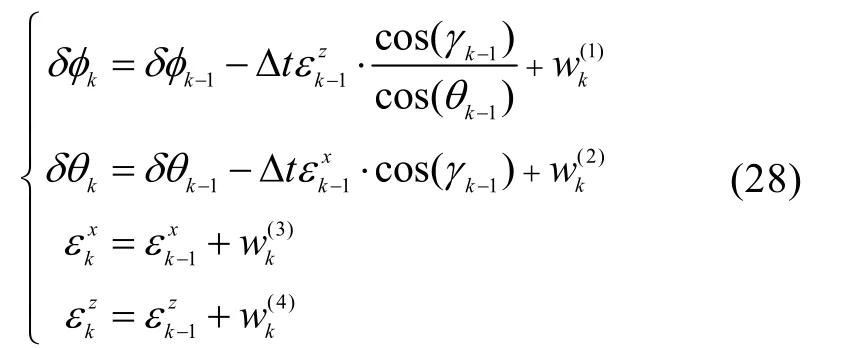
此时的MEMS陀螺仪在线标定可观测矩阵

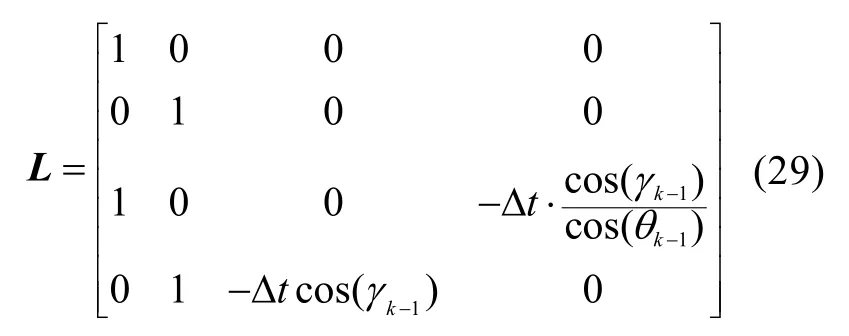
由于 UUV正常定深航行下,其俯仰角与横滚角仅有小幅度摆动,因此最简单有效的标定路径为从UUV定深定向航行。

综上所述,协同标定路径设计需要遵循以下原则:1)相邻3个量测时间的主从UUV距离观测方位角不同且从UUV定深定向航行。

3 仿真验证与分析

为了验证协同标定的有效性,利用MATLAB进行仿真验证。设定两轴MEMS陀螺仪陀螺漂移为10°/h;角度随机游走为 1°/h;从 UUV在载体系三轴上有摇摆的角速度,k时刻分别为

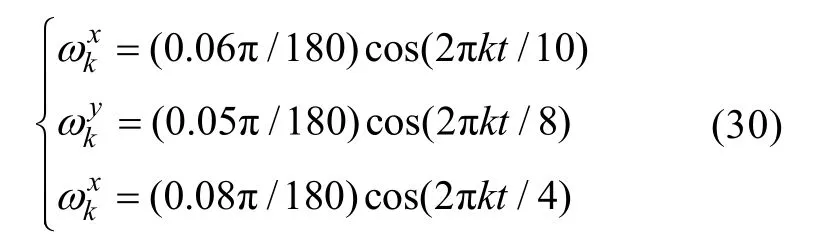
为了验证协同标定路径设计原则的有效性,设计3种路径,对两轴MEMES陀螺仪陀螺漂移进行解算,路径设计如下。

路径 1:主 UUV 初始位置(0,125),以速度2m/s沿固定航向角0°定深航行,从UUV初始位置(0,0),以速度3 m/s沿固定航向角10°定深航行;

路径 2:主 UUV 初始位置(0,125),以速度1m/s沿固定航向角0°定深航行,从UUV初始位置(0,0),以速度2 m/s沿固定航向角10°定深航行;

路径3:主UUV初始位置为(0,90),以速度1 m/s沿固定航向角0°方向定深航行;从UUV初始位置(0,0),以速度2 m/s沿固定航向角-5°定深航行。

3.1 路径1仿真

协同导航EKF滤波器初始设置如下[14-15]

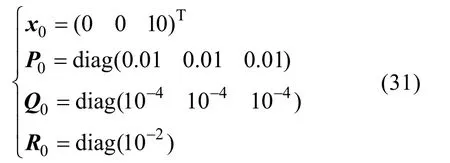
陀螺零偏标定KF滤波器初始设置如下

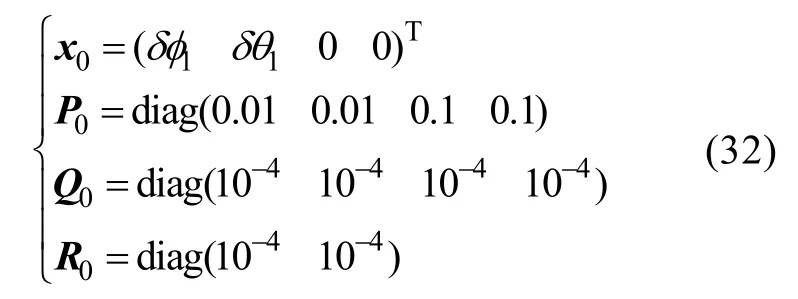
主、从UUV轨迹如图1所示。协同标定仿真结果如图 2所示。由图2可以看出,在路径 1下,1 min内滤波估计值趋于收敛,两轴MEMS陀螺漂移标定值为10°/h。

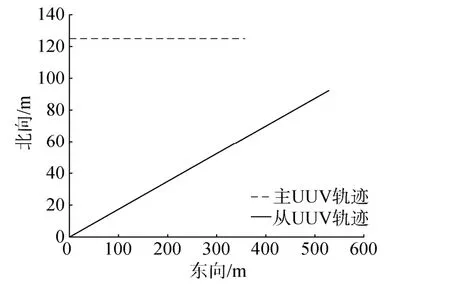
图1 路径1下主、从UUV轨迹Fig.1 Tracks of master and slave UUVs in path 1 test

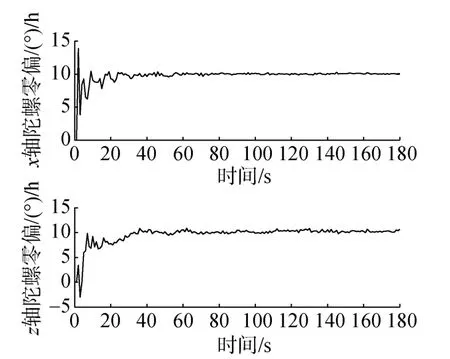
图2 路径1下微机电陀螺仪陀螺漂移估计结果Fig.2 Estimation results of gyro drift of micro-electro mechanical system(MEMS)gyroscope in path 1 test

图3为路径1下从UUV航行10 min时协同标定补偿结果图,可以看出没有进行标定补偿的定位误差在10 min后达30 m,而补偿后的轨迹与真实轨迹几乎完全重合。由局部放大图知,从 UUV补偿后定位误差不到1 m,导航精度得到极大提高。

3.2 路径2仿真

协同导航EKF滤波器初始设置如下

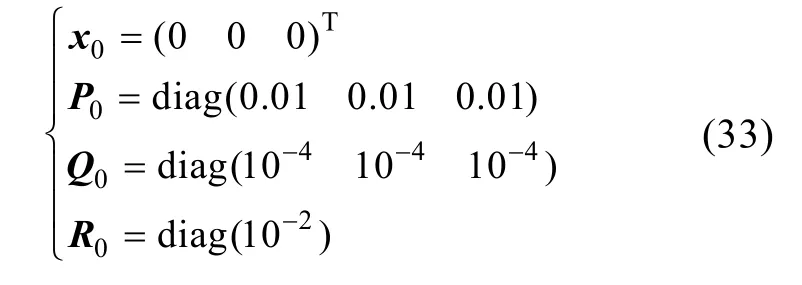
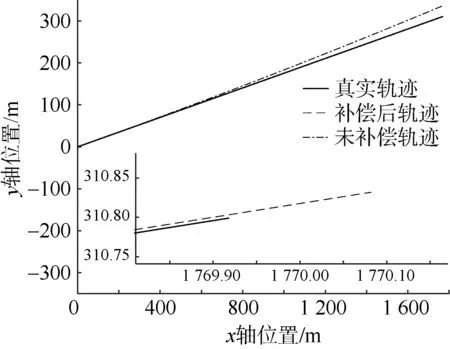
图3 路径1下协同标定补偿结果Fig.3 Results of collaborative calibration compensation in path 1 test

陀螺零偏标定KF滤波器初始设置如下

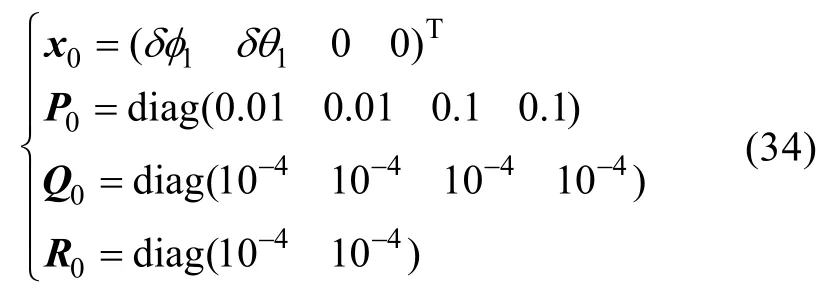
主、从UUV轨迹如图4所示。

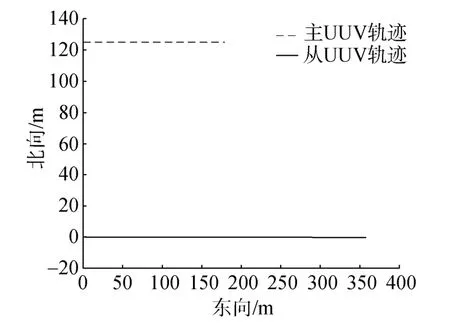
图4 路径2下主、从UUV轨迹Fig.4 Tracks of master and slave UUVs in path 2 test

协同标定仿真结果如图5所示。路径2下的协同标定补偿结果如图6所示。

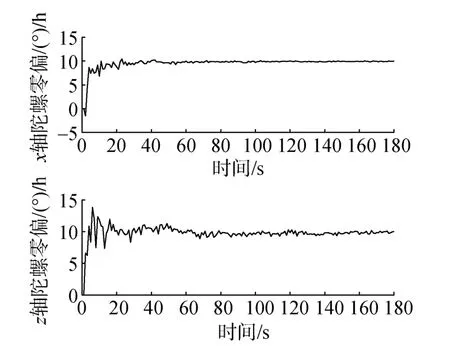
图5 路径2下MEMS陀螺仪陀螺漂移估计结果Fig.5 Estimation results of MEMS gyroscope gyro drift in path 2 test

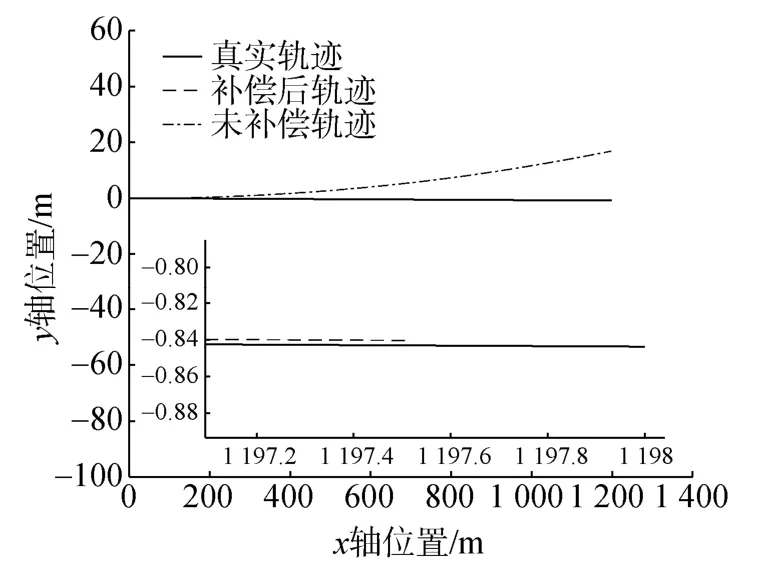
图6 路径2下协同标定补偿结果Fig.6 Results of collaborative calibration compensation in path 2 test

由图4～图6可以看出,在路径2下滤波估计值1 min内趋于收敛,MEMS陀螺零偏误差标定值为10°/h,标定补偿后从UUV导航精度得到极大提高。

3.3 路径3仿真

协同导航EKF滤波器初始设置如下

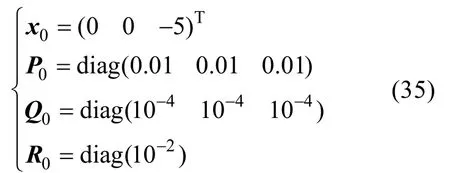
陀螺零偏标定KF滤波器初始设置如下

主、从UUV轨迹如图7所示。协同标定结果如图8所示。路径3下的协同标定补偿结果如图9所示。

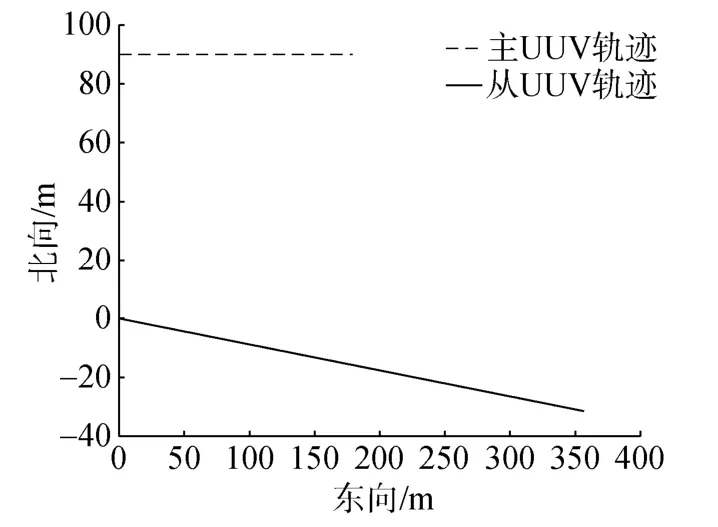
图7 路径3下主、从UUV轨迹Fig.7 Tracks of master and slave UUVs in path 3 test

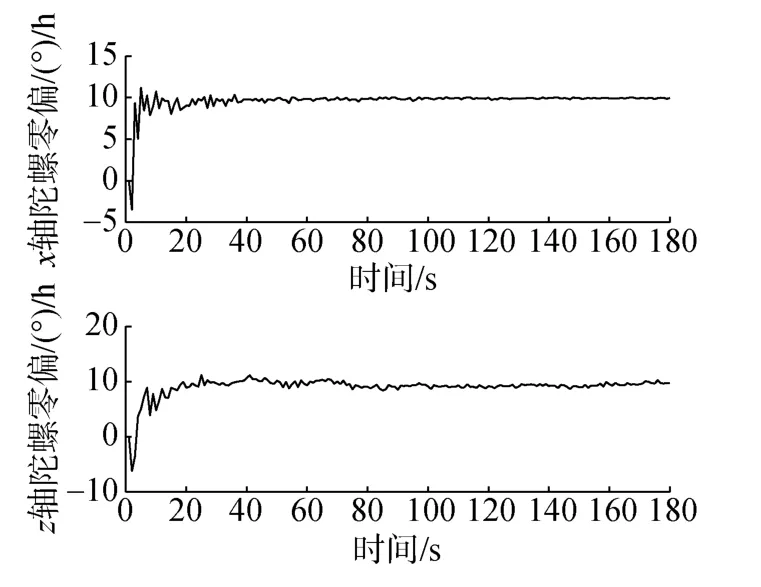
图8 路径3下MEMS陀螺陀螺仪漂移估计结果Fig.8 Estimation results of MEMS gyroscope gyro drift in path 3 test

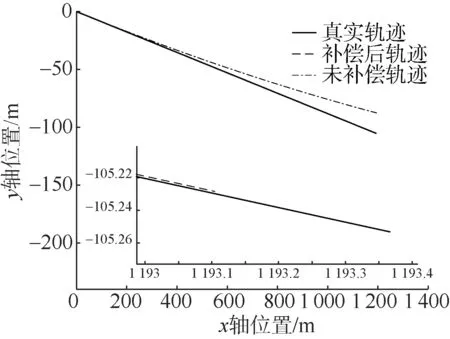
图9 路径3下协同标定补偿结果Fig.9 Results of collaborative calibration compensation in path 3 test

由图7～图9可以看出,在路径3下滤波估计值1 min内趋于收敛,MEMS陀螺零偏误差标定值为10°/h,标定补偿后,从UUV导航精度得到极大提高。

综上所述,在 3条标定路径下,在短时间内完成对两轴MEMS陀螺仪陀螺漂移的标定,补偿后的从 UUV导航误差明显减小。仿真结果验证了协同标定的有效性以及协同标定路径设计原则的准确性。

4 结束语

针对 UUV协同导航水声通信短时失效时协同导航不可用,且从 UUV配备的三轴地磁传感器与两轴微机电 MEMS陀螺仪组合姿态传感器中MEMS陀螺的陀螺漂移大,导致UUV航位推算精度差的问题,文中提出了 UUV协同导航下两轴 MEMS陀螺仪协同标定方法并推导了协同标定路径设计原则。利用基于EKF的协同导航结果作为标定观测量,在协同标定路径下在线解算MEMS陀螺仪漂移并补偿,提高了从 UUV自身导航精度。当主、从 UUV通信短时中断时,从UUV不需要上浮接受GPS信号校正自身导航误差,降低了从UUV能量消耗,增长了从UUV工作时间。仿真结果表明,文中提出的算法能够快速有效估计出 MEMS陀螺仪漂移,极大提高从UUV导航精度。考虑时间延迟等误差的从UUV协同标定将是下一步研究的重点。