大破口失水事故工况下碳化硅惰性氧化模型研究
钱立波,余红星,孙玉发,陈 伟,申亚欧
(中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610041)
福岛核事故暴露了传统UO2-Zr合金燃料在抵抗事故性能方面的不足,耐事故燃料(ATF)以其可有效提升燃料在事故工况下的安全特性逐渐成为国际核燃料领域新的研究方向之一。开发抗氧化性更好的新型包壳材料是耐事故燃料研究的重要内容之一。碳化硅(SiC)由于具有良好的耐高温、抗辐照和中子经济性,尤其是具有较锆合金更好的高温抗氧化特性,而成为耐事故新型包壳的主要研究方向之一。
若反应堆发生大破口失水事故(LB LOCA),SiC包壳处于低压、高温水蒸气环境,由于SiC在水蒸气中的氧化速率远大于在空气(氧气)中的氧化速率,且水蒸气也会与SiC的氧化产物SiO2反应生成挥发性的氢氧化硅,从而加速SiC的氧化过程[1]。但目前对SiC氧化特性的实验研究多集中在高温燃烧工况(空气、水蒸气混合气体环境),较少涉及高温纯水蒸气工况[2-4],且由于SiC氧化问题的复杂性,目前针对纯水蒸气气氛下SiC氧化模型的研究也较少。基于此,本文将针对大破口失水事故工况下低压、高温纯水蒸气气氛下SiC材料的氧化特性开展理论模型研究。
1 SiC在水蒸气中的惰性氧化过程
SiC在高温水蒸气中的氧化反应有两种类型:惰性氧化和活性氧化。在较高的水蒸气分压下,SiC表面会形成一层致密的SiO2膜,阻止SiC的进一步氧化(式(1)),这种氧化称为惰性氧化。在较低的水蒸气分压下,SiC表面会生成挥发性的SiO,导致SiC被快速氧化(活性氧化,式(2))。
SiC+3H2O(g)=SiO2+CO(g)+3H2(g)
(1)
SiC+2H2O(g)=SiO(g)+CO(g)+2H2(g)
(2)
在大破口失水事故下,SiC与水蒸气发生惰性氧化反应。SiC氧化产生的SiO2膜会与水蒸气反应生成挥发性的氢氧化硅[5]。
SiO2+2H2O(g)=Si(OH)4(g)
(3)
SiC在纯水蒸气中的惰性氧化过程包含图1所示的5个物理过程:1) H2O从主流扩散至SiO2膜表面;2) H2O通过SiO2膜扩散到SiO2/SiC界面;3) H2O在SiO2/SiC界面上与SiC反应;4) 氧化反应气态产物(CO、H2)在SiO2膜内扩散;5) 氧化反应气态产物(CO、H2)扩散到主流。

图1 SiC氧化和挥发反应示意图
在SiC氧化研究中,通常应用抛物线型氧化速率常数Kp(mg2/(cm4·h))表征氧化反应动力学特性,应用线性挥发速率常数Kl(mg/(cm2·h))表征挥发反应动力学特性[5],故SiC氧化生成的SiO2膜厚度变化特性如下:
(4)
其中:x为SiO2膜厚度;α为反应(1)中的相对分子质量(Mw)增量,α=Mw,SiO2/(Mw,O2-Mw,C)。
本文基于修正的Deal-Grove模型[6]和通道边界层内传热/传质类比法分别给出SiC的抛物线型氧化速率常数模型和SiO2的线性挥发速率常数模型。
2 抛物线型氧化速率常数Kp计算模型
2.1 Kp理论模型
如图2所示,假设SiC表面SiO2膜厚度为x,则水分子从主流体扩散至SiO2表面的扩散过程可表示为:
(5)
其中:F为水蒸气反应速率(对于H2和CO,F为产生速率);h为扩散系数;C为水蒸气浓度;上标∞代表主流体参数,s代表SiO2表面处参数;下标H2O代表水蒸气参数。
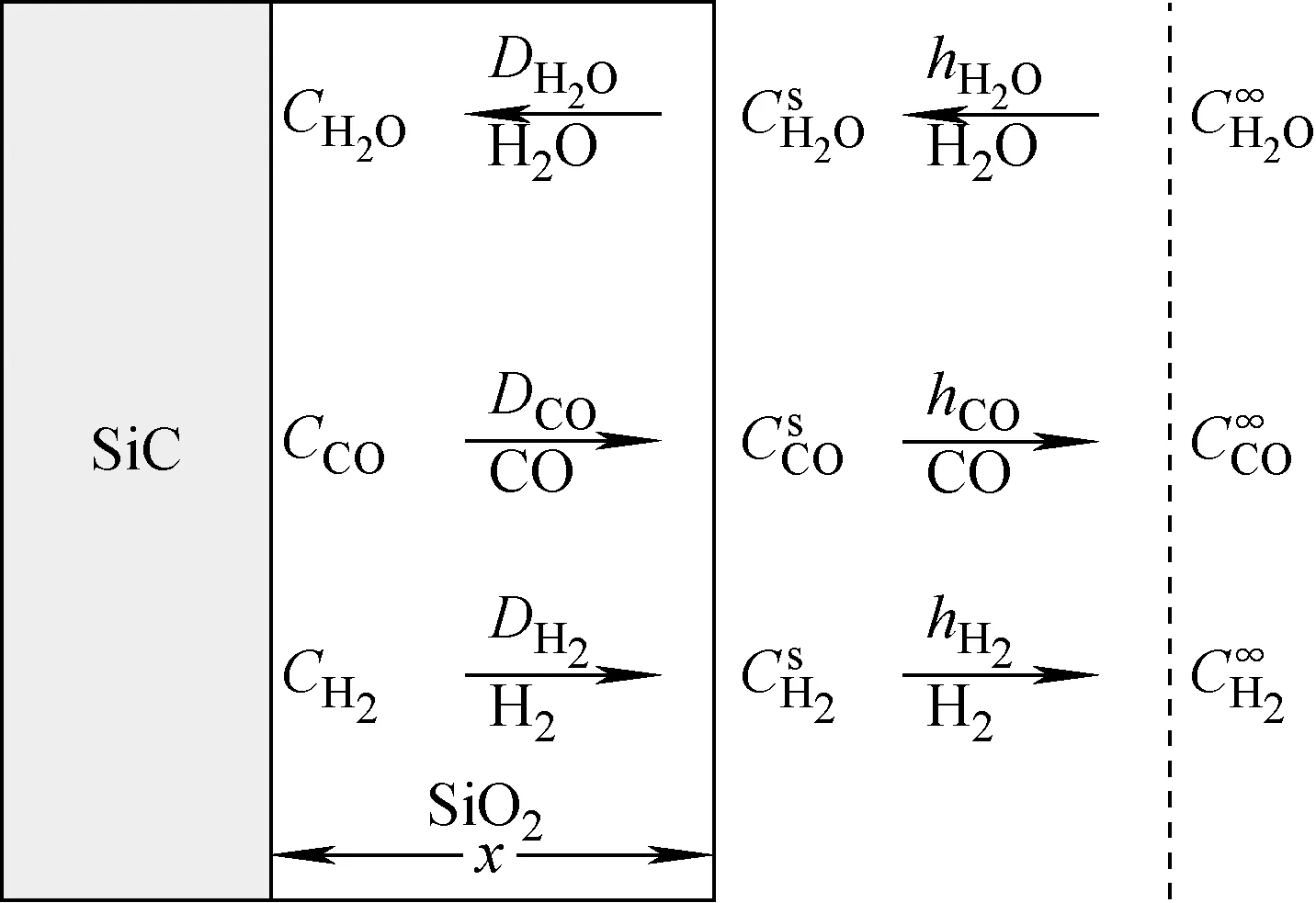
图2 SiC氧化反应原理示意图
稳态情况下,H2O在SiO2膜内的扩散过程可表示为:
(6)
其中,D为H2O在SiO2膜内的扩散系数。
氧化产物CO在SiO2膜内的扩散过程为:
(7)
氧化产物H2在SiO2膜内的扩散过程为:
(8)
由于H2在SiO2膜内的扩散速率远大于CO,因此CO在SiO2膜内的扩散是SiC氧化反应过程(4)的关键进程。
化学反应(1)发生在SiO2/SiC界面处,其反应速率可表示为:
F=KfCH2O-KrCCO
(9)
其中,Kf、Kr分别为式(1)正向反应和逆向反应常数。
稳态工况下,根据质量守恒,式(1)中反应速率、水蒸气反应速率和CO产生速率有如下关系:
F∶FH2O∶FCO=1∶3∶1
(10)
因此,由式(5)~(10)可得SiC的氧化反应速率:
(11)
SiO2膜厚度可通过式(1)的反应速率计算:
(12)
其中,N0为生成单位体积SiO2消耗的水分子数。
因此,SiO2膜厚度变化可表示为:
(13)
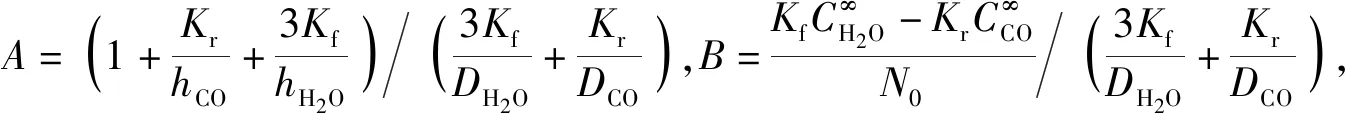
(14)
综合考虑SiC的氧化过程可知,过程(1)和过程(5)因水分子或氧化气态产物扩散速度较快,对氧化反应过程影响较小,因此不是控制氧化反应速率的关键过程。若SiC的氧化速率受界面反应控制(过程(3)),则氧化速率为常数,SiO2膜厚度与氧化时间呈线性关系;若氧化反应是由过程(2)或过程(4)控制,则氧化速率将随氧化时间的增加而减小,SiO2膜厚度变化遵循抛物线型规律。国内外SiC氧化实验研究结果表明,SiC在氧化反应初期以界面反应为主,SiO2膜厚度遵循线性规律;随着氧化反应的进行,扩散机制将占据主导地位,SiO2膜厚度变化遵循抛物线型规律,即目前研究认为扩散过程(过程(2)或过程(4))是SiC氧化的关键过程[7-8],与Si的氧化过程[9]和SiC在O2环境中的氧化过程[6]类似。SiC在水蒸气中的氧化也可分为线性阶段和抛物线型阶段。
1) SiO2膜线性增长阶段
氧化时间较短时,氧化反应过程(过程(3))是影响氧化速率的速度控制步骤:
(15)
2) SiO2膜抛物线型增长阶段
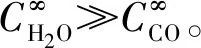
氧化时间较长时,SiO2膜厚度趋近于抛物线型,气体分子在SiO2膜内的扩散过程是速率控制步骤。国内外开展的纯水蒸气环境及氧气/水蒸气混合环境下的SiC氧化实验结果[2,5,10-13]显示,H2O在SiO2膜内的扩散过程(过程(2))是SiC氧化反应的关键进程,即Kf/DH2O≫Kr/DCO,故:
(16)
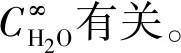
由于氧化层线性增长阶段时间较短,因此该阶段可忽略,式(14)可写为:
(17)
其中,B′=2B。
DH2O=DH2O,0exp(-Q/RT)
(18)
其中:DH2O,0为频率因子;Q为激活能;R为理想气体常数。
因此,B′最终可表示为如下形式:
(19)
由式(4)、(17)~(19)可得:
(20)
根据Opila等[16]的研究结果可知,SiC的氧化速率常数与水蒸气分压呈正比,即式(20)中水蒸气分压pH2O的指数为1,这也从侧面证明水分子在SiO2膜中的扩散过程是SiC氧化的控制性步骤。因此式(20)可变为:
Kp=AKppH2Oexp(-Q/RT)
(21)
其中:AKp为常数;pH2O为水蒸气压力,0.1 MPa;Q为活化能,J/mol。
2.2 Kp模型实验数据拟合
Opila[11]认为载气(Ar、O2)可能影响SiC在水蒸气中的氧化特性,因此在后续的研究[16]中为消除载气的影响,Opila采用固定气体组成比例的方法研究混合气体(H2O、O2、CO2、N2)下的SiC氧化特性,结果显示SiC的氧化速率常数与水蒸气分压呈正比。实际上,SiC在O2中的氧化速率常数远低于在H2O中的氧化速率常数,因此,混合气体中H2O是最主要的氧化剂,载气对SiC的氧化速率常数并无明显影响[11]。基于SiC在不同实验环境、不同水蒸气分压和温度工况下的氧化实验数据[2,5,11-12,16-19],拟合得到SiC的氧化速率常数为:
Kp=pH2Oexp(7.19-162 000/RT)
(22)
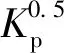
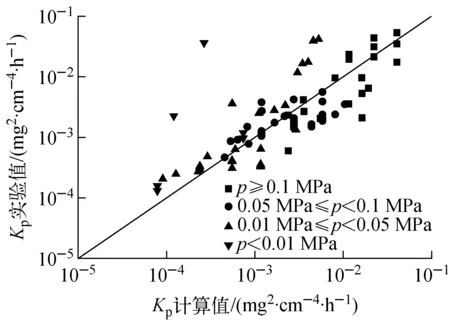
图3 SiC氧化计算模型计算结果与实验数据对比
3 线性挥发速率常数Kl计算模型
3.1 Kl理论模型
线性挥发速率常数Kl主要受挥发反应的气态产物(Si(OH)4)在流动边界层的扩散过程和环境温度影响,即Kl主要取决于SiO2膜表面的流动特性和环境温度。在大破口失水事故工况下,由于堆芯衰变热不断降低,堆芯区域的流动状态由层流-湍流过渡状态转变为层流状态。由于浮升力产生的动量方程源项Gr/Re2≪1[20],因此本质上大破口失水事故工况下堆芯可认为处于强迫流动状态。由于SiO2线性挥发反应速率相对较低,属于低质量传递速率问题,故传热与传质之间存在着简单类比,即近壁面处的无量纲温度梯度(Nusselt数)和无量纲浓度梯度(Sherwood数)具有相同的结构形式:
(23)
其中:h′、h′mat分别为表面传热和传质系数,h′mat=J/ρv,J为Si(OH)4的质量通量,ρv为Si(OH)4的密度,由平衡状态下SiO2与H2O的反应速率确定,与边界层内Si(OH)4的分压呈正比;De为当量直径;Θ为无量纲温度;C为无量纲浓度;Ddiff为Si(OH)4在边界层中的扩散系数,与水蒸气压力呈反比;x、y、z为直角坐标,y为垂直于壁面方向坐标;Re、Pr、Sc分别为无量纲Reynolds数、Prandtl数和Schmidt数。
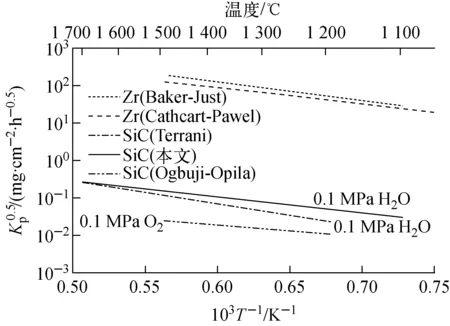
图4 水蒸气中锆合金与SiC氧化速率常数的对比
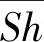
(24)
其中:L为通道长度;μf、μw分别为主流温度和壁面温度下的动力黏性系数。
由于主流中Si(OH)4的浓度很小(~0),故SiO2膜表面处Si(OH)4的质量通量J可表示为:
(25)
假设SiC氧化和SiO2挥发反应均为准稳态过程,即任意时刻均处于平衡状态,则SiO2表面处挥发反应(3)的平衡压力可写为:
(26)
其中,Keq为挥发反应平衡常数。
根据Gibbs自由能公式ΔrG⊖=ΔrH⊖-TΔrS⊖及Gibbs自由能等温方程ΔrG⊖=-RTlnKeq,假设在考虑的温度范围内,ΔrH⊖和ΔrS⊖为常数,因此可求得挥发反应平衡常数Keq:
(27)
其中:ΔrG⊖、ΔrH⊖和ΔrS⊖分别为挥发反应中标准Gibbs能变、焓变和熵变;A0为常数,A0=exp(ΔrS⊖/R)。

(28)
考虑实际传质过程与理论分析结果的差异,式(24)中水蒸气压力及Sh的指数需根据实验确定,因此可得:
(29)
SiO2的线性挥发速率常数与Si(OH)4的质量通量有如下对应关系:
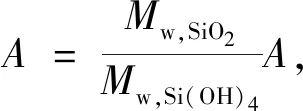
(30)
其中,A、ΔrH⊖、a、b可根据实验数据拟合获得,a取决于挥发反应与流动速度的相关性,压力项的指数b代表产生不同产物的不同的挥发反应,其取值与SiO2的挥发反应类型相关。
可见,式(30)与Opila等[5]的SiO2挥发反应速率公式具有相同的结构形式,二者最大的区别是Sherwood数的应用。
3.2 Kl模型实验数据拟合
由于SiCf/SiC包壳最外层为致密的β-SiC层,因此在该β-SiC层消失前,其氧化挥发特性与β-SiC相同[2]。目前,针对纯水蒸气环境下的SiC氧化挥发实验结果较少,主要集中在α-SiC和β-SiC材料上。由于生产工艺的差异,α-SiC和β-SiC的杂质含量及密度差异较大,但由于α-SiC与β-SiC具有相当的热力学稳定性[22-23],其挥发速率相差并不显著。Opila等[5]开展的SiC在水蒸气/氧气环境中的氧化挥发试验结果显示,SiC中的杂质仅影响SiC氧化生成SiO2的过程,对SiO2材料挥发反应的影响可忽略;Robinson等[4]实验研究了α-SiC和β-SiC在燃烧环境条件下的氧化特性,结果显示二者仅相差约1%~3%;Tortorelli等[1]在1 MPa空气/水蒸气混合环境下和Lee[13]在0.1 MPa水蒸气环境下开展的SiC氧化挥发实验结果也支持这一结论。因此,本文在拟合SiC线性挥发速率时,主要包括α-SiC和β-SiC在纯水蒸气环境中的实验结果[2,13,24-25]。
当SiC氧化实验压力为0.1 MPa时,将水蒸气压力的影响归并在系数A中,最终得到SiO2线性挥发速率常数拟合公式:
(31)
其中:ReD为以当量直径De为特征长度的Reynolds数,ReD=ρvDe/μ,ρ为水蒸气密度,μ为水蒸气动力黏性系数,v为水蒸气流速;L为通道长度,m。
图5为式(31)计算结果与实验值的对比,可见绝大部分实验数据位于±30%误差限内。由式(31)可见,低压下线性挥发速率常数与水蒸气流速的0.42次方呈正比,略大于根据层流传热/传质类比法对应的系数(0.33),与Opila[26]针对SiC开展的氧化实验研究获得的层流下水蒸气流速指数(~v0.5)以及Sudhir等[27]开展的Si3N4氧化实验获得的SiO2挥发反应速率常数(~v0.5)相近。可见,低压下水蒸气流动可近似为层流流动,且以层流换热Sider-Tate公式为基础的传热/传质类比方法是合理的。
图6为相同冷却剂通道下不同线性挥发速率常数计算模型的结果对比。
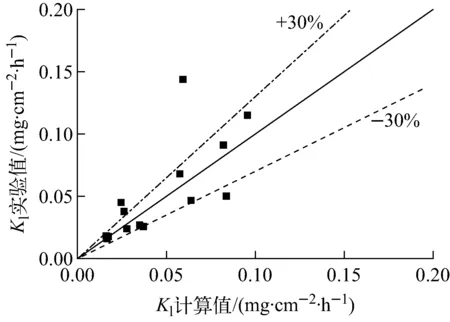
图5 线性挥发速率常数理论计算值与实验值对比
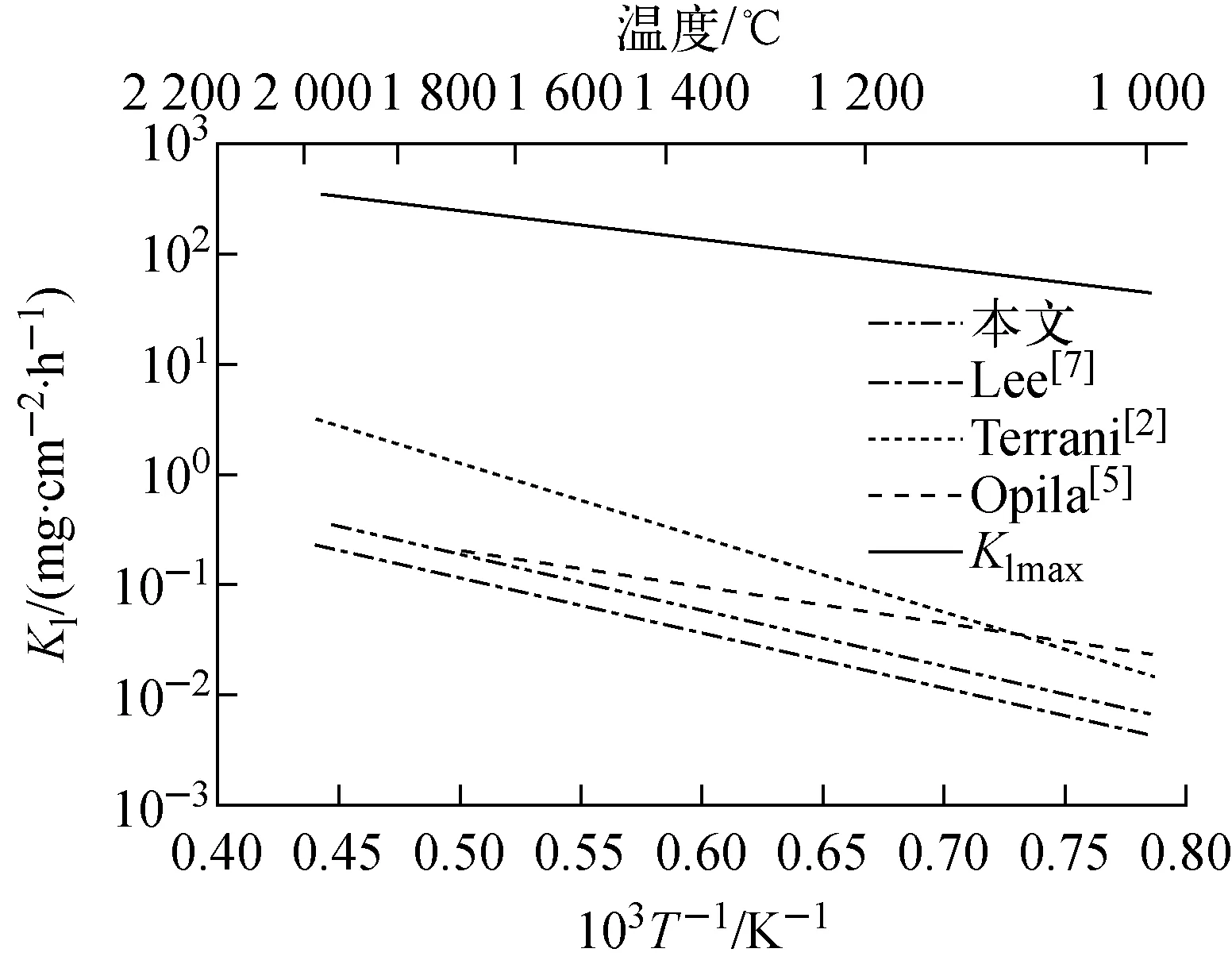
图6 不同Kl计算模型的计算结果对比
从图6可看出,Opila公式[5]和Terrani公式[2]计算得到的线性挥发速率常数均高于本模型获得的。这是由于Opila公式基于无限大平板层流边界层理论,Terrani公式基于纯SiO2块在水蒸气环境中的线性挥发速率常数实验结果,公式中的速度项为主流速度,未考虑流动边界层的影响,因此二者均不适用于通道内由于SiC氧化产生的SiO2的线性挥发速率常数计算;本文的SiO2线性挥发模型与Lee公式[7]均基于通道内流动边界层理论,二者也具有相似的变化趋势,但本方法结果较Lee公式更保守。所有公式计算的线性挥发速率常数均远低于假设流动边界层厚度为0时的极限线性挥发速率常数(Klmax)[27],如图6所示。
(32)
此外,Lee公式、Terrani公式、Opila公式以及本文模型给出的线性挥发速率常数随温度呈单调增加,即温度越高,线性挥发速率常数越大。
3.3 SiC复合包壳最外层SiC损耗厚度计算
SiC复合包壳分为3层:内层由高密度单体成型的SiC组成,作为裂变气体的主要屏障;中间层为连续的SiC织网与SiC基体组成复合编织层,提供堆内运行期间所需的高强度与硬度;外层也由高密度单体成型的SiC组成,作为对外界环境的屏障。高温氧化环境下中间SiC纤维层的热解炭界面层会发生氧化反应导致SiC纤维层强度严重降级,因此,大破口失水事故工况下SiC复合包壳最外层SiC应具有足够的厚度,以防止中间SiC纤维层与高温水蒸气直接接触。
本文开发的SiC高温水蒸气环境下的线性挥发速率常数模型可用于估算最外层SiC的损耗厚度。基于Si原子守恒,根据SiO2线性挥发速率常数模型可计算SiC层的损耗速率Δ:
(33)
其中,ρSiC为SiC密度。
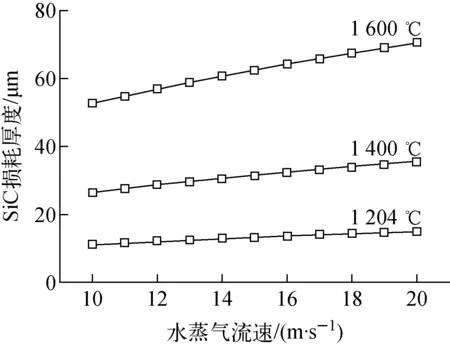
图7 72 h内大破口失水事故工况下SiC复合包壳最外层SiC的损耗厚度
图7为不同水蒸气温度及流速下最外层SiC的损耗厚度。可看出,最外层SiC的损耗与氧化环境(水蒸气温度和流速)密切相关。在1 600、1 400、1 204 ℃水蒸气环境下,72 h内最外层SiC的损耗厚度分别不超过80、40、20 μm。对于Zr合金,在1 204 ℃水蒸气环境下1 h的损耗厚度即超过175 μm(Cathcart-Pawel模型)。可见,SiC材料可提升核反应堆燃料在大破口失水事故工况下的安全特性,可有效缓解事故后果。
4 结论
本文主要研究了大破口失水事故工况下SiC的抛物线型氧化速率常数模型和SiO2的线性挥发速率常数模型。
1) 基于修正的Deal-Grove模型,获得了SiC材料的抛物线型氧化速率模型。结果显示,SiC在高温水蒸气环境中的氧化速率常数较锆合金低约2~3个数量级,SiC在高温水蒸气环境中的氧化速率常数较在氧气环境下高约1个数量级。
2) 基于传热/传质类比法,获得了低压高温水蒸气环境下SiC氧化生成的SiO2膜线性挥发速率常数模型,模型计算误差与实验结果误差在30%以内。
3) 本文开发得到的SiO2线性挥发速率常数模型可用于估算SiC复合包壳最外层SiC的损耗速率,为确定SiC复合包壳最外层SiC的厚度提供一定的理论依据。

