不等温分布下燃料棒径向温度相关238U共振吸收截面计算
张 乾,王 超,姜 荣,3,赵 强,吴宏春,娄 磊
(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001;2.中广核研究院有限公司,广东 深圳 518031;3.中国科学技术大学 工程与应用物理系,安徽 合肥 230026;4.西安交通大学 核科学与技术学院,陕西 西安 710049;5.中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610213)
在燃料棒性能和数值分析中,需精确计算燃料棒的径向功率分布。由于238U强烈的共振自屏效应,其燃料棒径向上的共振中子吸收截面(简称吸收截面)存在空间分布,并受到不等温分布的影响,功率分布的计算需精确计算这种情况下燃料棒径向共振吸收截面。
处理上述问题的传统方法是基于空间相关的丹科夫方法(SDDM, spatially dependent Dancoff method)[1],该方法采用了不同温度下的共振积分进行插值,是Stamm’ler方法的扩展[2]。研究表明[3-5],SDDM在进行以能群为单位的截面预测时存在显著误差。为提高计算精度又发展了子群方法,该方法采用关系模型、子群参数调整法和核子数密度调整法[6-8]处理该问题,但关系模型需对子群结构进行特殊处理,而子群水平调整法和核子数密度调整法均采用半经验公式,适用性有限。
精度较高的方法是求解基于超细群(UFG, ultra-fine-group)能群结构的中子慢化方程,又称超细群方法。该方法可用于传统等价理论的误差修正以及共振干涉效应的精确处理[9-11],但在燃料棒内部不等温分布下,计算燃料分区间的中子首次飞行碰撞概率(简称碰撞概率)引入的计算量较大。针对该问题,相关研究者[12]提出了基于等温假设的碰撞概率模型。该模型近似认为不等温系统的碰撞概率等同于等温系统,可减少计算时间。但数值验证发现[13],该模型在进行238U共振吸收截面计算时,会造成燃料内部的共振吸收截面被低估,将导致无限增殖因数的计算出现偏差。
本文提出一种基于温度扰动的超细群慢化方程对238U的径向共振吸收截面进行计算,并与MCNP5[14]的统计结果进行比较。
1 理论模型
1.1 超细群慢化方程和基于等温假设的碰撞概率模型
超细群慢化方程是在中子输运方程的基础上忽略裂变源项,基于非均匀系统中各分区之间的中子首次飞行碰撞概率建立的中子平衡方程,其形式如下:
(1)
其中:i、j为区域编号;Vi为区域体积;Σt,i(E)为与能量E相关的宏观总截面;φi(E)和Qj(E)分别为中子标通量密度和源项;Pji为区域j至i的碰撞概率。
在精细能群结构(4~9 118 eV之间按等勒宽划分39 000群)的基础上,从最高能群递归求解式(1),即可获得φ(E)在超细群能群结构上的精细能谱。有效共振自屏截面的定义为:
(2)
其中:g为能群;Σ(E)为与能量相关的宏观截面;Σg为g群的有效共振自屏截面。
将能谱φ(E)代入式(2)即可计算得到有效共振自屏截面。由式(1)可知,求解慢化方程的关键在于碰撞概率Pji的计算,而Pji与宏观总截面Σt,i(E)相关。在超细群慢化方程求解的能量范围内,Σt,i(E)会呈现共振现象,直接由Σt,i(E)在线计算碰撞概率非常耗时,故在基于碰撞概率方法(CPM, collision probability method)的组件计算程序(如SRAC程序[15])中,常采用预设Pji与Σt,i(E)插值表的形式,对Pji进行快速插值计算。对于1个压水堆燃料栅元,如图1a所示,将燃料棒在径向按等体积划分10环。在等温分布的前提下,各环的连续能量宏观总截面Σt,i(E)在多普勒展宽后可视为相同,故可预先计算若干Σt,i(E)下的Pji,形成插值表,在实际求解式(1)时进行快速插值计算。如图1b所示,如果在径向存在不等温分布,则Pji的计算与10环的燃料温度相关,如果建立Pji与10个燃料区域的Σt,i(E)的10维插值表,计算量太大。另一方面,如果对Pji进行在线计算,由于式(1)需在超细群结构上求解39 000次,Pji的计算量也很大。
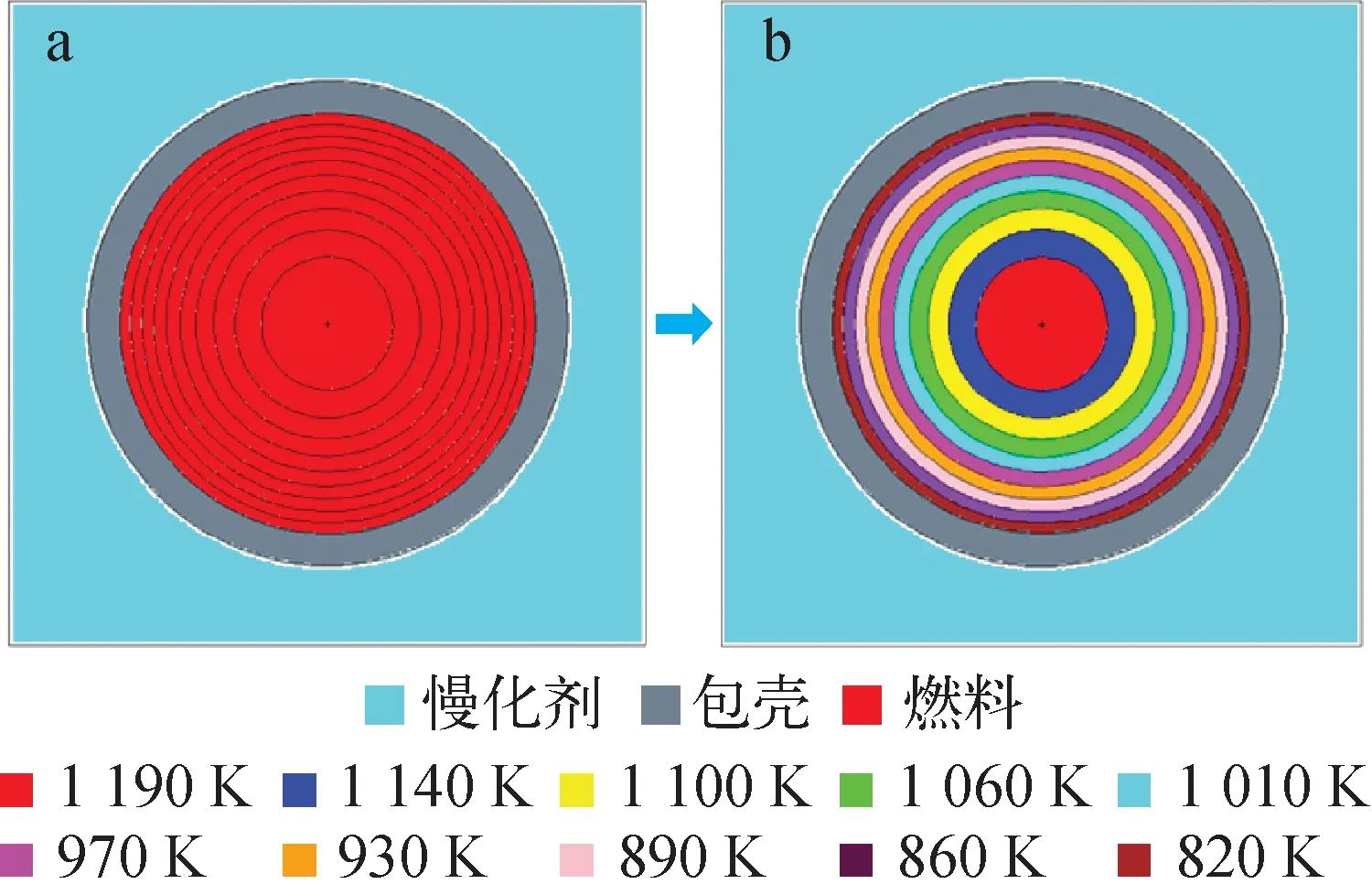
图1 燃料棒径向分区(a)与不等温分布(b)示意图
为解决碰撞概率计算量的问题,MPACT程序[12]提出了一种基于等温假设的碰撞概率模型:
(3)
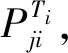
1.2 基于温度扰动模型的超细群方法
在SRAC程序中,针对系统中出现两种不同的共振吸收体,式(1)的碰撞概率的求解需建立1个二维的插值表P(Σ1(E),Σ2(E)),预先制作1个二维碰撞概率插值表的计算量是可接受的。对图1b所示的燃料分区中,存在10个不同的温度分区,可认为共有10种共振吸收体,SRAC程序中的二维碰撞概率插值表是无法直接使用的。
如果能将燃料区中10种不同温度的分区问题分解为只存在两种温度的情况,则SRAC程序的二维碰撞概率插值表就可使用。根据这种思路,提出了温度扰动模型,并定义如下影响因子:
(4)
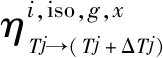
类似地,假设在该等温系统中,单独对k区的温度Tk产生了扰动ΔTk,则其影响因子为:
(5)
假设对j区和k区的温度同时进行扰动,两个燃料区的温度变化对燃料棒整体的能谱有共同的影响,则该影响因子为:
(6)
观察式(4)~(6),近似假设对j区和k区的温度同时扰动产生的影响因子等于对j区和k区的温度单独进行扰动的影响因子之乘积,则有:
(7)
式(7)的物理含义为,对于等温分布的燃料棒,同时扰动多个燃料区的温度对共振截面的影响,可分解为单独扰动各燃料区的温度对共振截面影响的乘积。基于该假设,对于图1b中的不等温分布问题,可认为是在等温分布下对10个区域的温度进行扰动的结果,则任意区域、任意核素的各能群的反应截面可近似表示为:
(8)
根据式(8),基于温度扰动模型的超细群方法计算不等温问题的步骤如下:1) 首先基于超细群方法,计算等温条件下各分区、核素、能群的各种反应截面,等温温度可选取各区温度的平均值;2) 分别扰动第1~10区的温度进行超细群计算,获得新的截面并记录每种扰动引起的η;3) 将10次扰动引起的η相乘,通过式(8)计算最终的共振截面。
由上述步骤,超细群程序共执行11次,其中等温分布问题中只包含1个共振吸收体,而其他问题的计算中只包含两个共振吸收体。因此,基于二维碰撞概率插值表的超细群程序就可应用于这套计算流程。
2 数值验证
2.1 截面的计算精度
选取如图1所示的压水堆栅元问题,其几何与材料分别来自于日本原子能院发布的下一代轻水堆UO2单栅元基准题[16]。燃料棒沿径向等体积划分为10环,由内至外分别为1~10区。基于SRAC程序的PEACO模块[15],开发了1套基于二维碰撞概率插值表的超细群慢化方程求解程序UFP。利用NJOY程序[17]对ENDF-B/Ⅶ进行处理得到特定温度点下的点截面文件,作为UFP的数据库。UFP程序的能群结构为从4~9 118 eV间均等的对数能降划分。计算出超细群通量后,基于WIMS的69群能群结构[18]的15~27共振能群进行多群截面的归并。
问题的基准来自于MCNP5的统计结果。各温度点的ACE格式数据库由NJOY程序生成,每代100 000个粒子,计算500代,舍弃100代,统计问题中各燃料区、各核素的微观吸收反应率和中子通量密度,通过反应率除以通量获得截面。由于燃料中共振自屏效应的主要来源是238U对中子的共振吸收截面,所以需重点对该截面进行分析。
利用UFP程序分别采用温度扰动模型和等温碰撞概率模型对压水堆栅元问题进行了计算,并以MCNP5统计结果为基准进行了比较。图2示出两种模型在第1、4区的238U微观吸收截面相对于MCNP5结果的偏差。图3示出两种模型在第23能群(48.052~75.5 eV)和第27能群(4~9.877 eV)的微观吸收截面的相对偏差在径向的分布。
由图2可看出,燃料的内部区域,等温碰撞概率模型所预测的238U微观吸收截面明显偏低,且靠近中心的第1区的相对偏差更大。这些偏差中,较大的相对偏差主要出现在较低的能量范围内(<150 eV)。可以推测,由于238U的微观吸收截面在较低能量范围的共振峰较宽,共振峰截面较高,所以共振效应更强,而等温碰撞概率模型引入的近似会造成更大的偏差。由图3可看出,等温碰撞概率模型的计算偏差在燃料棒靠近表面的分区较低,而在靠近中心的分区偏差增大,这与图2的结论匹配。由图2、3可见,温度扰动模型均取得了相对精确的微观截面计算结果,相对偏差小于2%。
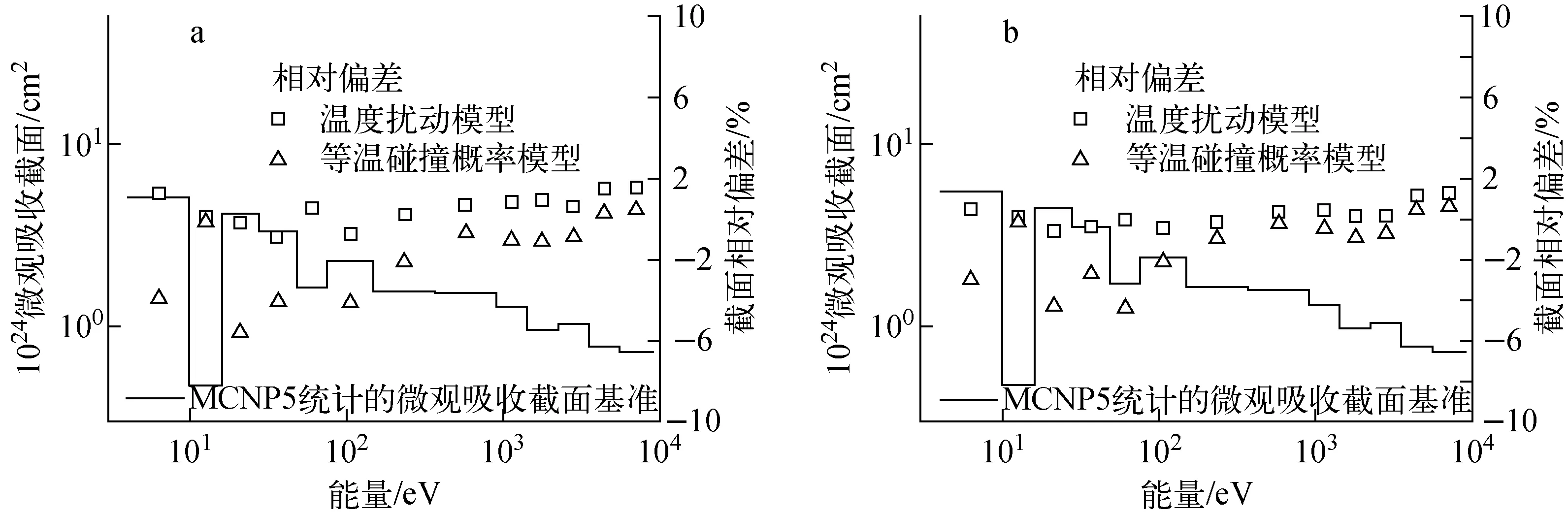
a——第1区;b——第4区图2 238U微观吸收截面的相对偏差
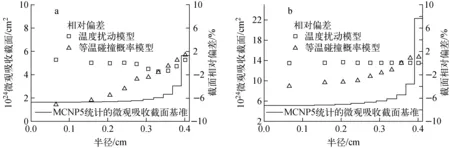
a——第23群;b——第27群图3 238U微观吸收截面相对偏差在径向的分布
2.2 反应率与无限增殖因数精度
为进一步分析温度扰动模型和等温碰撞概率模型的共振计算精度对输运计算的影响,针对图1所示的压水堆单栅元问题,以两种模型所计算的微观吸收截面作为输入数据,分别进行中子输运计算,获得反应率和无限增殖因数,用于评估两种模型对最终中子学计算的影响。中子输运计算采用了模块化特征线计算程序MOCHA[19]。
为分析两种模型在多种问题下的精度,设计了10组单栅元问题,10组单栅元问题的参数列于表1,采用的3种不等温分布数据列于表2。表1中:问题1为2.1节压水堆栅元问题,对比问题1、2可评估两种共振计算模型在不同燃料成分下的精度;对比问题1、3、4、5可评估两种模型在不同富集度问题下的精度;对比问题1、6、7、8可评估两种模型在不同水铀比下的精度;对比问题1、9、10可评估两种模型在不同温度梯度下的精度。
采用MOCHA程序进行输运计算得到的238U微观吸收反应率偏差可通过下式计算:
(9)
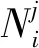
表3、4分别列出等温碰撞概率模型和温度扰动模型的238U微观吸收反应率的偏差。
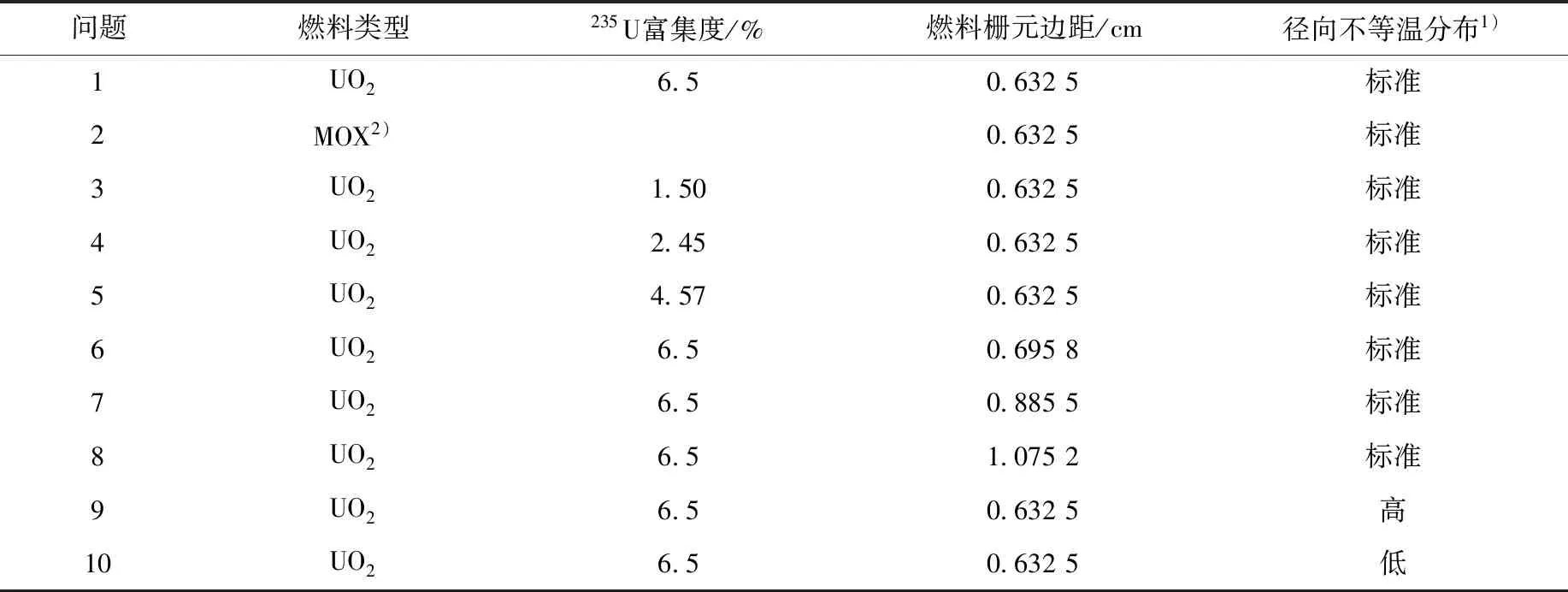
表1 10组压水堆单栅元问题描述
注:1) 径向不等温分布的具体数据见表2
2) MOX燃料的成分取自日本原子能院发布的新一代轻水堆基准题[16]
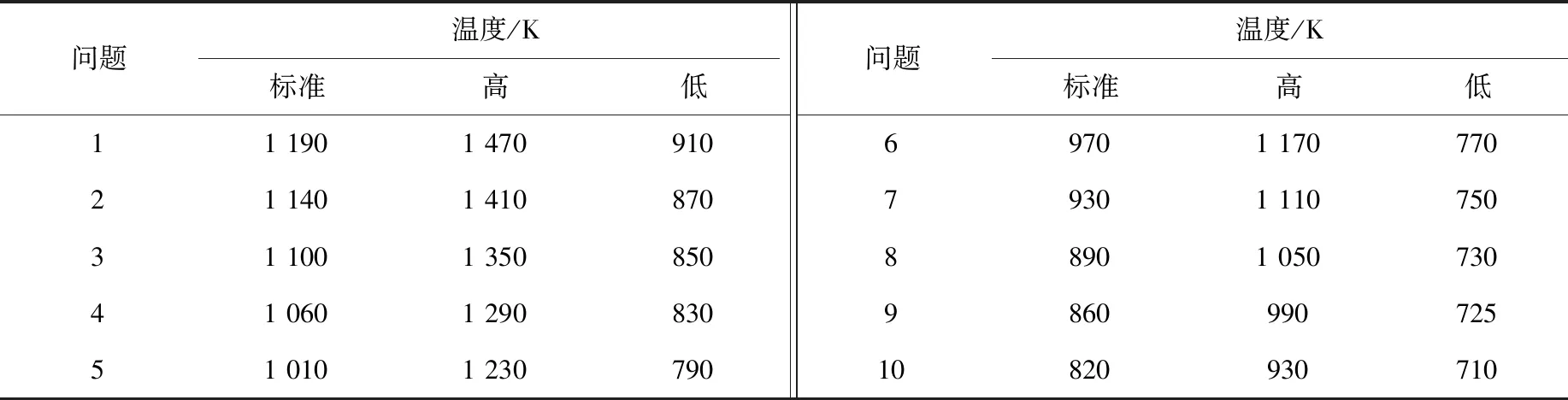
表2 燃料棒径向不等温分布
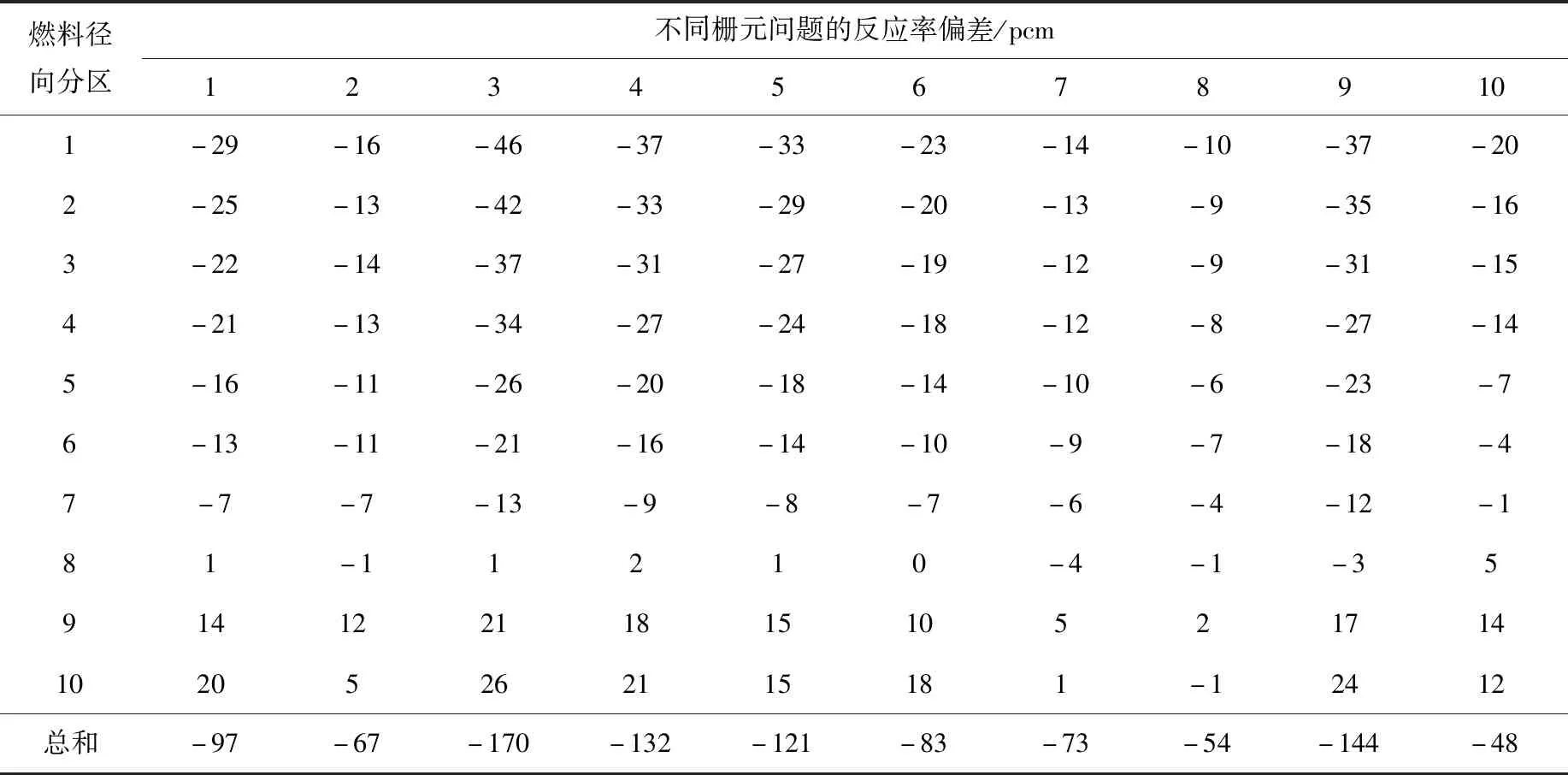
表3 等温碰撞概率模型的238U微观吸收反应率偏差
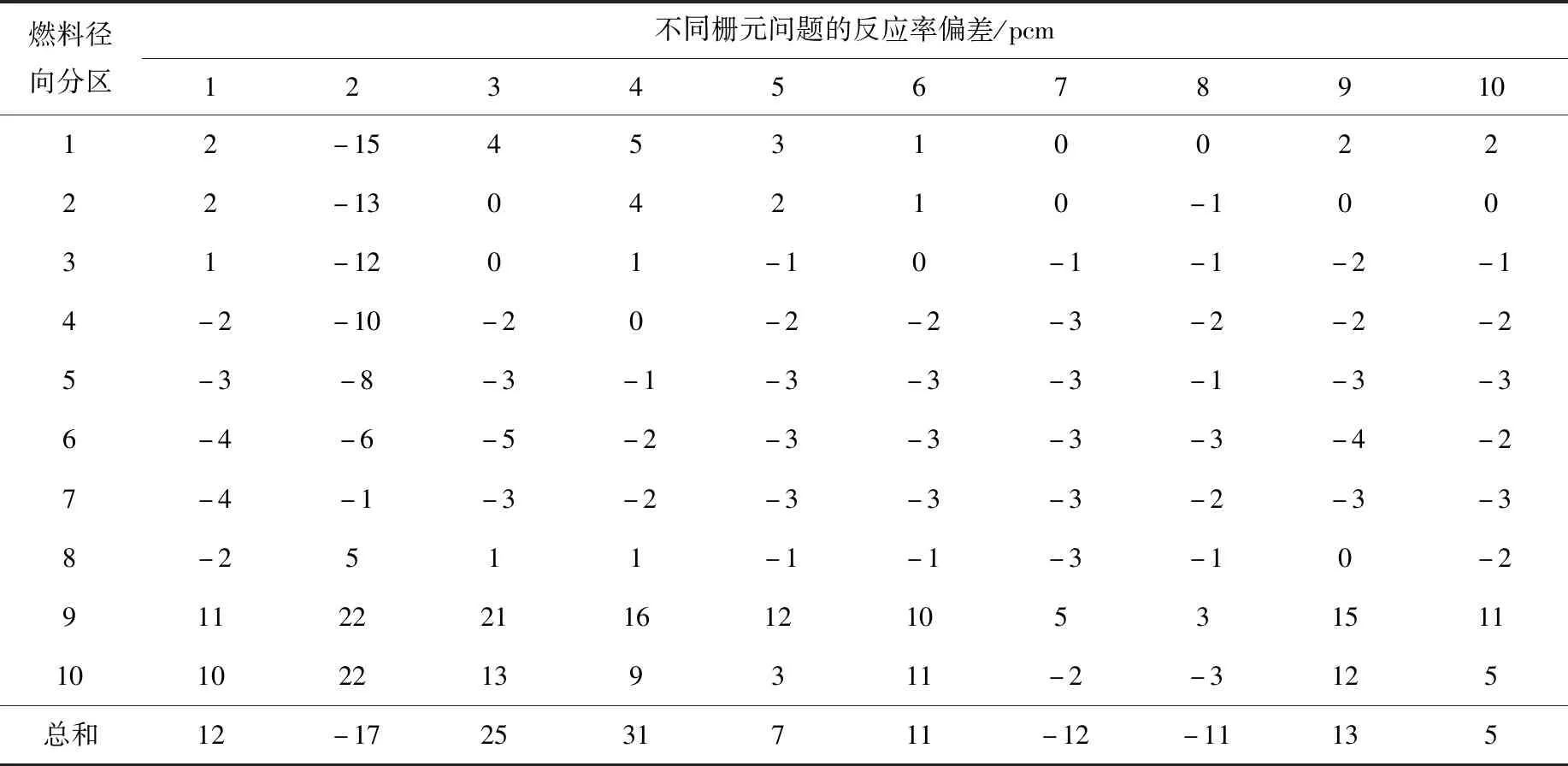
表4 温度扰动模型的238U微观吸收反应率偏差
由表3中问题1、3、4和5的结果可见,等温碰撞概率模型的238U微观吸收反应率偏差随燃料富集度的减小而增大;由问题1、6、7和8的结果可见,等温碰撞概率模型的偏差随水铀比的增大而减小;从问题1、9和10可见,等温碰撞概率模型的偏差随径向温度梯度增大而增大。由表3、4可知,等温碰撞概率模型在燃料棒靠近中心处的微观吸收反应率偏差较大,且越靠近中心偏差越大,而温度扰动模型在大多数问题和分区中精度较高。
由2.1节可知,等温碰撞概率模型低估了238U在燃料内部区域的共振吸收现象。计算内部分区时,如第1区,其温度为1 190 K,此时等温碰撞概率模型在外围的温度也达到了1 190 K,而实际的最外区温度只有820 K。根据多普勒展宽原理,温度越高时共振吸收越强,那么等温碰撞概率模型高估了中子在燃料外区的吸收,导致中子在燃料棒中的逃逸概率比实际偏低。根据等价理论[3],偏低的中子逃脱概率会降低中子在238U核素的共振吸收,导致偏低的微观吸收截面。本文提出的基于式(8)的温度扰动模型考虑了各区的温度对燃料棒内部径向中子能谱的综合影响,其截面和反应率的计算精度更高,更接近MCNP5的统计结果。
表5列出两种模型计算的无限增殖因数的偏差。基准解来自于由MCNP5统计的微观吸收截面作为输入、以MOCHA程序进行计算的结果。由表5可看出,等温碰撞概率模型所计算的无限增殖因数偏大,偏差约在100~200 pcm之间,主要原因是燃料棒内部分区的238U共振吸收截面被低估。温度扰动模型的精度较高,偏差在10~50 pcm范围内。可见,本文提出的温度扰动模型提升了共振计算精度。
从计算流程看,等温碰撞概率模型需计算10个温度点下的碰撞概率,相当于10次超细群计算。温度扰动模型需计算等温分布问题和两区温度问题共11次,加之二维碰撞概率插值表的使用,计算消耗略高于等温碰撞概率模型,但远小于碰撞概率的在线计算和MCNP5的统计过程。因此,本文提出的温度扰动模型在略高于等温碰撞概率模型的计算消耗下,达到了更高的共振计算精度。

表5 单栅元问题的无限增殖因数偏差
3 结论
针对不等温分布下与燃料棒径向温度相关的共振计算问题,提出了一种基于温度扰动模型的超细群方法。温度扰动模型将不等温分布对燃料棒分区共振截面的影响,分解为单独分区的温度扰动带来的影响,并通过乘积的方式,达到对最终结果的修正。采用了基于两维碰撞概率插值的超细群方法进行计算,避免了碰撞概率的在线求解,节省了计算时间。结果表明,对于压水堆单栅元基准问题,温度扰动模型可将截面计算相对偏差控制在2%以下。通过改变基准问题设计了10组不同的压水堆栅元问题并进行了计算,结果表明温度扰动模型具有较高的反应率计算精度,其无限增殖因数偏差在50 pcm以下。此外,温度扰动模型的计算消耗小于碰撞概率的在线计算和MCNP5的统计过程,在保证精度的同时具备较高的计算效率。

