高温气冷堆不确定性分析的新进展

郭 炯，李 富，王黎东，卢佳楠，郭 建，牛进林，王毅箴，邬颖杰，刘保坤，崔梦蕾

(清华大学 核能与新能源技术研究院，先进核能技术协同创新中心，先进反应堆工程与安全教育部重点实验室，北京 100084)

随着核能技术的发展，对于反应堆系统的某些重要安全参数，提供“最佳估计值+不确定性范围”的需求日益增长[1]。目前关于轻水堆(LWR)计算不确定性的国际性合作研究项目已经实施，如OECD/NEA LWR UAM项目[2-3]，并取得了一定进展。高温气冷堆(HTR)的计算不确定性分析开展得较晚。2012年，IAEA启动了HTR计算模型不确定性分析的国际合作协调项目(IAEA CRP on HTGR UAM)[4]，旨在推进HTR相关的计算不确定性分析，清华大学核能与新能源技术研究院(核研院)也参与了该项目。

但由于球床高温气冷堆(PB-HTR)与LWR在堆芯结构方面差别很大，LWR计算不确定性的分析框架和分析工具难以直接用于HTR的分析。核研院借鉴LWR计算不确定性的分析成果，并结合HTR设计上的特殊性及模型要求，对PB-HTR的计算不确定性开展了研究。本文介绍PB-HTR计算不确定性分析的新进展。

1 HTR不确定性分析的特殊性

在反应堆计算不确定性的研究领域，LWR的相关研究已基本成熟，建立了“系统分解，逐级传递”的分析思路。在此基础上，国内外多家研究机构取得了很多研究成果和进展[5-7]，这些方法均是HTR不确定性研究的技术基础。但由于PB-HTR在堆芯结构和运行方式上的特殊性，使得PB-HTR的不确定性分析具有不同的特点，LWR中的分析框架和分析工具尚不能完全解决HTR的问题[8]。PB-HTR不确定性分析的特殊性主要体现在以下几方面。

1) HTR采用流动球床堆芯。其堆芯由燃料球堆积而成；燃料球从堆顶装入，自堆底卸出，从上到下通过堆芯；采用燃耗球“多次通过”的运行方式。对于这种堆芯的模拟，以VSOP程序[9]为例，通常是将堆芯活性区在径向上划分为几个流道，并在轴向上划分为若干个区域，通过将燃料球沿着流道从上一区域移动到下面的区域来模拟球床流动。两次燃料球流动的时间间隔称为倒料步，在1个倒料步内，可采用标准的能谱计算、堆芯扩散计算和燃耗计算进行物理分析。因此，对于堆内的1个区域，其内部同时包含了处于不同燃耗水平的燃料球，在不同的倒料步，1个区域内的燃料核素成分也不断变化。在该情况下，其内部的燃耗累积与传统LWR固定组件位置的燃耗累积方式有很大区别。对于球床堆芯的模拟计算，由于每个区域的燃料核素成分会发生变化，所以在每次倒料之后均会重新基于新的核素组成进行能谱计算和全堆扩散计算。在这种情况下，其中子物理、热工、燃耗计算及球流运动是紧密耦合的。以核数据为开端的物理计算，很难拆分成独立的计算分析环节，尤其是对平衡堆芯这种典型状态进行不确定性分析，原有LWR的分析框架和计算工具将不再适用。

2) 在堆芯设计和建模上的特殊性。首先作为石墨慢化堆芯，其在中子学特性上与传统LWR有所不同，如中子慢化长度较长，在中子物理分析过程中通常采用4能群结构等。另外PB-HTR是使用球形燃料元件堆积而成的球床堆芯结构，其需分析的堆芯结构参数与传统LWR也有显著区别，如球床密实度、燃料元件装铀量、球流混流等因素，这些均需特殊考虑。

3) 关注的不确定性传播终点不同。对于模块化PB-HTR，其设计强调固有安全性，即在任何事故条件下，堆芯的衰变热均可非能动载出，并保持燃料温度小于燃料最高温度的限值1 620 ℃[10]。对高温堆来说，在最严重事故情况下(即失冷失压事故)，燃料最高温度的不确定度是关系到PB-HTR固有安全性的关键参数。这一点不同于LWR的安全分析中对于偏离泡核沸腾比(DNBR)点的关注。因此，HTR计算不确定性分析，是以事故条件下燃料最高温度为传播终点，其不确定度需涵盖PB-HTR中各环节的不确定性因素。

2 HTR不确定性分析的框架

HTR计算不确定性分析框架的建立借鉴了LWR的分析思路：首先将复杂的反应堆系统区分为不同的模块，理清每个模块的不确定性来源及输入；然后计算不确定性因素在各计算环节中的传递及其对堆芯关键参数的影响；以事故条件下燃料最高温度的不确定性作为各种不确定性因素传递的终点。具体的不确定性分析框架如图1[8]所示。

从图1可见，HTR的不确定性分析是从基础截面核数据库不确定性源头出发，定量分析其在堆芯物理计算中的传递，并加入球床堆芯参数的不确定性输入，如燃料球装铀量、球床密实度等不确定性因素，同时分析燃料球多次通过的运行方式的影响，最终得到堆芯功率分布、keff及其他堆芯参数的不确定性范围。然后再加入热工参数的不确定性影响因素，最终得到事故条件下燃料最高温度的不确定性范围。目前研究主要集中在反应堆物理相关的不确定性分析领域。

图1 HTR系统不确定性分析框架

3 不确定性分析工具VSOP-UAM程序的开发

目前已有的不确定性分析工具，大多是为了LWR的不确定性分析而开发的，如SCALE软件包[11]，其能实现对固定堆芯状态的不确定性分析。但目前仍缺少能真实反映球床堆运行特性的不确定性分析程序。为实现PB-HTR的不确定性完整分析，开发了新的分析程序VSOP-UAM[12]。

新程序充分利用了VSOP程序能完整模拟PB-HTR实际运行过程的优势，基于抽样理论，将VSOP程序作为计算黑箱，通过扰动基础核截面数据库的方式实现核截面不确定性的输入，最后再对计算得到的关键参数进行统计分析。该方法有效避免了对复杂耦合系统的系统分解，能实现对某些关键参数的直接分析。程序中使用如下方法。

1) 核数据扰动方法

VSOP-UAM程序中所用的核数据不确定性输入，来源于SCALE软件包中已经过综合评价的56群协方差数据库。而VSOP程序中，其数据库采用热中子能区30群和快中子能区68群结构。因此，需将基于56群协方差库生成的扰动系数转换成与VSOP核数据库一致的能群结构[13]。

在进行能群转换的过程中，采用勒能量加权方法，其主要方法为：

(1) 根据56群能群结构和VSOP数据库的目标能群结构定义联合能量网格，联合能量网格中的能群分割点包含了56群能群和VSOP数据库能群中所有的能群分界点；

(2) 将56群扰动系数映射到联合能量网格能群上，若联合网格能群i包含于56群中的某一群g，则将g群的扰动系数赋予网格；

(3) 根据联合网格能群和VSOP数据库目标能群结构，以勒能量u为权重归并扰动系数。

此外，SCALE核数据库中的协方差信息是分核素、分反应道给出的，在扰动VSOP的核数据库时，还要保证两种截面类型的一致性。图2示出了SCALE软件包以及VSOP程序中定义的核数据类型，可见两个程序的定义是有一定差别的。

图2 SCALE程序与VSOP程序中截面定义的关系

对于俘获吸收截面的定义，由于σ101=σ102+σ103+σ104+σ105+σ106+σ107，并且通过查看协方差矩阵，发现102～107截面之间基本没有相关性，因此协方差库中的截面、相对标准差和相对协方差可通过加和的方法直接求出。

对于散射截面定义，VSOP程序的数据库中是以群间转移矩阵的方式保存的，在这种情况下，需假定本群到各群的散射截面的扰动相同。

2) 隐式效应分析方法

在共振计算环节，无限稀释截面的不确定性经过共振计算对有效自屏截面的影响称为隐式效应。由于SCALE的核数据库中给出的是无限稀释截面的协方差信息，因此需结合VSOP程序的计算框架合理处理共振核素的隐式效应。

在VSOP程序的核截面数据库中，共振核素的截面是分为基础截面和共振参数信息存储，分别存储在不同的数据库中。其中共振参数信息首先需由VSOP程序中的共振处理模块VSOP-ZUT进行处理，将共振参数信息整理成与基础截面能群结构相同的共振积分数据库，用于插值计算有效共振吸收增量。

经过详细研究VSOP-ZUT程序计算流程及其与VSOP-MS主程序的数据交互关系，本文在目前VSOP-ZUT程序计算流程的基础上，增加了无限稀释截面扰动模块，基于SCALE软件提供的协方差信息，于程序外部提供各能群无限稀释截面的扰动系数，当程序对共振截面参数进行处理时，根据其所属能群乘上相应的扰动系数，即直接为VSOP主程序计算提供与基础核数据扰动一致的共振积分库，从而实现核数据不确定性显式和隐式效应的完整分析，并在VSOP-ZUT程序的基础上形成ZUT-SS程序。

最终，结合了隐式效应分析能力的PB-HTR不确定性程序VSOP-UAM的分析框架如图3所示。

图3 VSOP-UAM程序计算流程

4 PB-HTR不确定性特性分析

本文的PB-HTR不确定性特性分析主要利用自主开发的VSOP-UAM程序和SCALE6.2/TSUNAMI-3D模块。两个软件均能分析燃料球的双重非均匀性[14]，SCALE6.2程序具有良好的几何建模能力，可对燃料球模型、堆芯单元模型和初装堆芯模型进行不确定性定量分析；VSOP-UAM程序可对高温堆的初装堆芯模型和平衡堆芯模型进行定量分析。两个程序具有不同的计算分析能力，同时其功能也有一定的重合度，可用于某些结果的对比验证。

结合IAEA CRP的任务框架，目前已完成了球床堆燃料球、堆芯单元模型、初装堆芯以及平衡堆芯几种模型的不确定性分析，获得了定量分析结果和一些初步结论。

1) 燃料球和堆芯单元模型[15]

单个燃料球模型和堆芯单元模型是PB-HTR中最基础的中子物理计算模型。通过研究燃料球和堆芯单元这样几何比较简单、物质组成比较单一的模型，能分离复杂系统的影响，从而更加清晰地研究核数据不确定性对PB-HTR的影响机理。这一步是堆芯建模不确定性分析的基础。

图4 燃料球模型和堆芯单元模型示意图

在研究中使用的燃料球模型和堆芯单元模型定义如图4所示。其中燃料球分为燃料区和石墨包壳区，燃料区采用3层包覆结构(TRISO)颗粒规则排列的模型。堆芯单元模型采用体心立方排布，栅距设置为对应0.61的填充率；模型中间位置是1个完整的燃料球，周围8个1/8球可填充不同的物质，模拟球床堆芯不同位置处的能谱环境。使用这种体心立方排布的单元结构，与燃料球在堆芯中的实际分布状况类似，可有效描述所分析燃料球的周围燃料环境，评估在不同情况下的不确定性范围。

通过对计算模型中富集度、温度以及燃耗等影响因素的分析，可得到如下初步结论：单个燃料球无限增殖因数k∞的不确定度在0.50%～0.58%之间，堆芯单元各种组合k∞的不确定度在0.48%～0.55%之间；作为石墨慢化的系统，石墨的俘获吸收截面有较大的不确定性贡献，也导致了高温堆系统的不确定性较LWR的略大；而随着燃料球温度的升高，由于多普勒效应，使238U的俘获吸收贡献增加，导致两种模型的不确定度均有所增加；而随着富集度的增加，新燃料的不确定度有所降低，这主要是由于238U和石墨C的俘获吸收贡献减小。

在研究的过程中同时发现，对于带有一定燃耗的燃料球，使用SCALE程序中56群数据库和44群数据库分别进行计算，其k∞的不确定性分析结果偏差很大，有较大贡献的核素截面对的排序差别也很大[16]。以常温条件(293 K)下的新燃料球计算模型为例，使用56群协方差数据库的keff不确定度为0.556，使用44群协方差数据库的keff不确定度为0.516。而在达到堆芯平均燃耗水平的燃料球计算模型中，使用56群协方差数据库的keff不确定度为0.516，使用44群协方差数据库的keff不确定度为0.554。可见使用两个数据库的计算结果具有明显的差别。

2) 初装堆芯模型

PB-HTR的初装堆芯状态是将新燃料球与石墨球按照一定比例混合，并且未经过功率运行的无燃耗堆芯状态。因此SCALE/TSUNAMI-3D程序与VSOP-UAM程序均具有计算分析能力，可利用两个程序分别建模分析。

针对HTR-PM的初装堆芯进行了建模分析，其模型参数如下：冷态温度为293 K，活性区高为11 m、半径为1.5 m，底部为6.05 m高的石墨球，上部为4.95 m高、4.2%富集度的新燃料球与石墨球以7∶8混合，填充率为0.61，控制棒全部提出，模型示意图如图5所示。

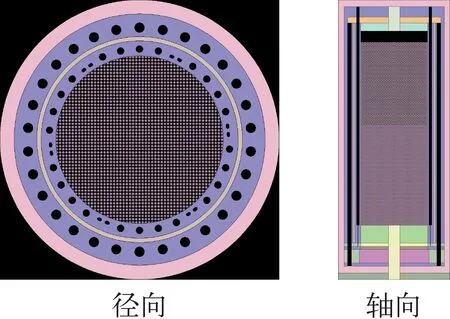
图5 初装堆芯的径向和轴向结构示意图

TSUNAMI-3D程序的敏感性分析采用微扰方法；VSOP-UAM程序采用统计学抽样方法，样本量为1 000。初装堆芯模型keff的不确定度如下：SCALE/TSUNAMI-3D程序为0.682 21%，VSOP-UAM程序为0.683 94%，差异为0.25%。初装堆芯主要核素截面对keff的不确定性贡献列于表1。

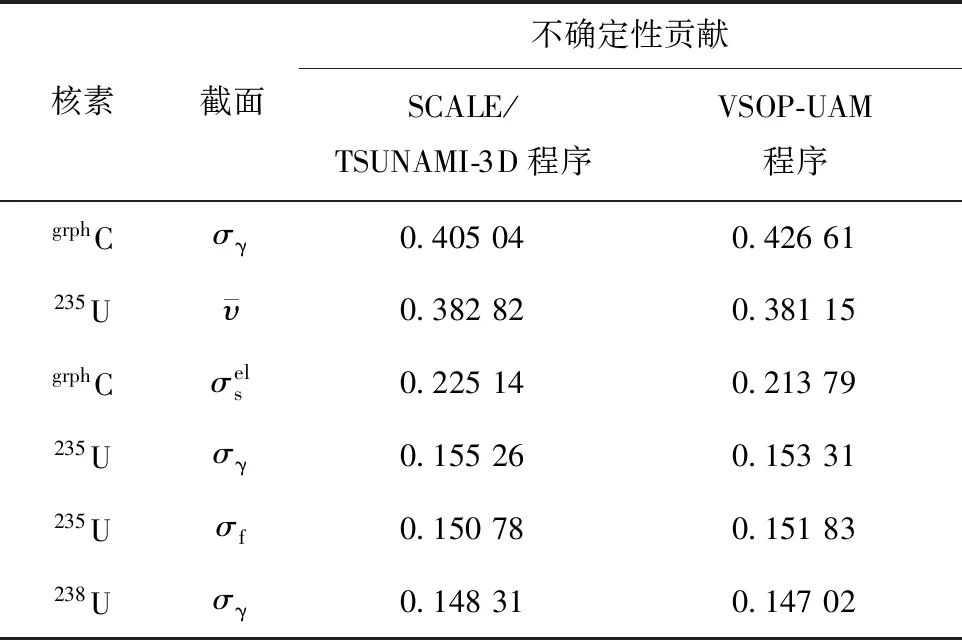
表1 初装堆芯主要核素截面对keff的不确定性贡献

从初装堆芯模型的keff不确定度可见，两个程序的计算结果符合得很好，考虑到VSOP-UAM程序采用了1 000个样本，其不确定度对应的95%置信区间为[0.655 21，0.715 40]，该置信区间包含了TSUNAMI-3D程序给出的计算结果，从表1可见，几个重要反应截面的不确定性贡献结果也吻合得很好。这也证明了VSOP-UAM程序的正确性。在初装堆模型中，其堆芯keff的不确定度达0.68%，该结果较一般LWR燃料循环初期(BOC)的不确定度大。这主要是由于初装堆芯中石墨的含量多，石墨的俘获吸收截面具有较大的不确定性，从而造成堆芯整体的不确定度偏大。通过分析核素截面对的不确定性贡献可见，石墨的俘获吸收截面对系统不确定性的贡献最大。

对于HTR-10实验堆的建模计算也得到了类似的分析结果。

3) 平衡堆芯模型

PB-HTR经过一段时间运行后，堆芯会进入平衡堆芯阶段。目前球床堆设计采用燃料球多次通过的运行方式，即燃料球需多次通过堆芯才能达到最终的卸料燃耗限值。不同设计方案下，燃料球可有不同的通过次数。为研究燃料多次通过的运行方式对堆芯关键参数的影响，设计了3种多次通过方案，即8次通过、10次通过和15次通过，控制3种设计方案的卸料燃耗均为90 000 MW·d/t(U)。使用VSOP-UAM程序对几种模型分别进行了计算。计算中选定的样本数量为1 000，以keff和功率峰值因子为目标参数进行分析。

表2列出了不同设计方案下，几种堆芯状态的keff的不确定度。

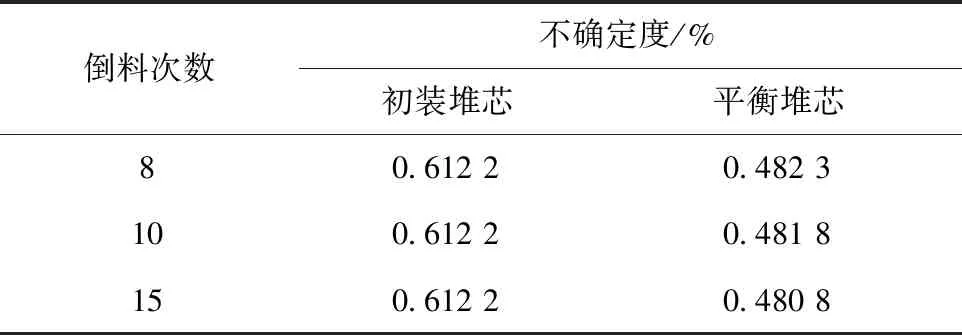
表2 平衡堆芯模型keff的不确定度

结果显示，平衡堆芯条件下，堆芯keff的不确定度约为0.48%，较初装堆芯的不确定度略低。这主要是因为VSOP-UAM程序采用了SCALE软件中的56群协方差数据库，其中239Pu的不确定性很小。由于平衡堆芯中235U的含量降低，而新产生的239Pu核素的不确定性贡献很小，因此使平衡堆芯的整体不确定度降低。此外，由于目前的VSOP-UAM程序中尚未考虑燃耗链相关的不确定性，因此，相关重金属和裂变产物的累积量暂时还无法进行不确定性分析。

同时数值计算结果显示，多次通过的运行方式可展平功率分布、降低功率峰值因子，通过次数越多，功率峰值因子越小。仍以表2中的计算模型为例，功率峰值因子如下：8次通过的为2.167 0，10次通过的为2.068 5，15次通过的为1.934 4。几种不同设计方案的功率峰值因子的不确定度均约为0.9%。

4) 堆芯结构参数的不确定性分析

同时，对HTR的相关堆芯参数也进行了不确定性分析。目前主要分析了3个参数的影响，分别为球流混流效应、燃料富集度和堆芯填充率。

VSOP程序中是通过将燃料球沿着流道从上一区域移动到下面的区域来模拟球床流动。通过给出每个流道的1个区域内的燃料球向相邻流道交混的比例，使每个区域的燃料向本流道下一个区域移动时，改成部分向本流道下一区域、部分向相邻流道的下一区域移动，以此模拟VSOP程序的框架下的球流混流效应。通过设置不同直流、混流系数，在同一平衡态堆芯基础上重复上述扰动得到不同堆芯状态[17]。

对于堆芯填充率和装铀量的分析采用类似方法，即对于在VSOP程序中划分的100个堆芯区域，按照给定的分布随机抽取每个区域的填充率，共抽取N组样本，然后将其作为输入参数导入VSOP程序进行模拟计算，得到N组计算结果进行统计分析。在计算中认为堆芯各区域的堆芯填充率和装铀量均服从正态分布，堆芯填充率的分布范围为0.605～0.615，燃料球装铀量的分布范围为6.65～7.35 g[18]。

计算结果表明，PB-HTR堆芯的球流混流效应对功率峰值的影响很小。即使堆芯中混流效应很强烈时，设置其直流份额为0.5时，功率峰值变化仅为0.091 273%。实际上，根据二维球流实验，堆芯各流道间混流份额约为1%[19]。在这种情况下，由于球流混流效应造成功率峰值计算不确定度约为0.002%，对keff的影响就更小。由于球床堆芯填充率的不确定性引起的最大功率密度变化为0.7%，其keff的不确定性在0.02%以内。由于燃料球装铀量的不确定性引起的最大功率密度变化为0.05%，其keff的不确定性在0.000 5%以内。

5 结论

PB-HTR由于流动球床的堆芯结构和运行方式，导致其计算不确定性具有不同于一般LWR的特殊性。清华大学核研院针对PB-HTR不确定性进行了研究，并取得了一定的进展，具体如下：

1) 针对球床高温堆的特殊问题，理清各项不确定性来源，建立了以事故条件下燃料最高温度为不确定性传递终点的不确定性分析框架；

2) 基于VSOP程序，开发了能反映PB-HTR实际运行特点的不确定性分析程序VSOP-UAM，实现了核数据不确定性隐式效应和显式效应的完整分析；

3) 对球床堆的燃料元件、堆芯单元以及堆芯模型分别开展了不确定性分析，分析结果显示，由于采用石墨慢化材料，HTR源于核数据的不确定性稍大于LWR的不确定性结果，初装堆芯的不确定度约为0.68%，平衡堆芯的不确定度约为0.48%；

4) 燃料球多次通过的运行方式能有效降低功率峰值因子，但对不确定性的影响尚需深入分析；

5) 对堆芯的球流混流效应、球床孔隙率和燃料球装铀量也进行了不确定性分析，分析结果表明，这些参数的不确定性对堆芯keff以及最大功率密度的影响很小，其不确定性的范围均在1%以内。