全陶瓷微密封燃料有效多群截面计算方法研究

尹 文，祖铁军，贺清明，曹良志

(西安交通大学 核科学与技术学院 ，陕西 西安 710049)

全陶瓷微密封(FCM)燃料是一种弥散颗粒燃料，也是一种事故容错燃料(ATF)，燃料区由基质和TRISO燃料颗粒组成[1]。FCM燃料存在双重非均匀性，分别是燃料棒内燃料颗粒的非均匀性和燃料棒的非均匀性。传统的共振计算方法[2-5]无法处理FCM燃料的双重非均匀性。针对双重非均匀性效应对自屏计算提出的挑战，国际上开展了大量研究[6]。第1类方法是基于双重非均匀系统输运理论的方法，该方法由Hébert[7]和Sanchez等[8]分别提出，由于该方法需要建立三维的输运方程进行求解，因此计算代价较大。第2类方法是采用常规燃料的自屏计算方法计算颗粒的有效自屏截面，然后采用丹可夫修正因子对截面进行修正，考虑双重非均匀性对有效自屏截面的影响，但该方法不能对颗粒和基质进行均匀化处理，一般直接采用体积权重得到自屏截面，会引入计算偏差[9]。第3类方法是采用缺陷因子方法对颗粒和基质进行均匀化处理，将双重非均匀系统转化为等效的单重非均匀系统，然后采用常规燃料的自屏计算方法计算等效系统的有效自屏截面，该方法最早由Jülich研究中心提出并应用于VSOP程序，该方法通过求解超细群慢化方程或通过穿透概率及碰撞概率等价得到缺陷因子，并用缺陷因子修正超细群或多群截面从而将基质和TRISO颗粒均匀化[10]，能方便地应用于现有的程序中。

为能更加精确地对FCM燃料进行自屏计算，本文基于超细群方法建立FCM燃料的有效多群截面计算方法，分别对双重非均匀性进行处理，通过缺陷因子修正所有核素的截面将燃料和基质均匀化，均匀化后的FCM燃料组件即可视为普通压水堆组件进行共振计算，通过求解超细群慢化方程从而得到共振能量段的有效自屏截面。

1 理论模型

FCM燃料存在双重非均匀性，在共振自屏计算中必须考虑。FCM燃料的双重非均匀性分别指燃料棒内TRISO颗粒的非均匀性以及FCM燃料棒的非均匀性。TRISO燃料颗粒不仅在共振能区有非常强烈的非均匀效应，而且在热能区也存在较强的非均匀效应，因此必须对TRISO颗粒的热能区也进行自屏处理[11]。对于燃料棒内TRISO颗粒的非均匀性采用缺陷因子方法对颗粒和基质进行均匀化处理。对于FCM燃料棒的非均匀效应通过丹可夫修正因子等效得到等效一维棒模型来描述[12-13]。最后，对所有一维棒模型求解超细群慢化方程从而得到共振能量段的有效自屏截面。计算流程如图1所示。

1.1 超细群方法

超细群中子慢化方程可写为：

(1)

式中：Σi,g为第g群i区总截面；φi,g为第g群i区中子通量密度；Vi和Vj分别为第i和第j区体积；Qj,g为第g群j区的源项，可采用递推计算得到；Pj,i,g为第g群中子从j区到i区的碰撞概率，可通过数值积分得到。

图1 FCM燃料有效多群截面计算流程图

求解方程(1)即可得到超细群中子通量。采用下式即可归并得到有效自屏截面：

(2)

式中：σi,k,g为第i区、k核素、多群g的有效自屏截面；σi,k,h为第i区、k核素、超细群h的截面；φi,h为第i区、超细群h的中子通量密度。

1.2 等效均匀化方法

1) 共振能区等效均匀化模型

为将共振能区燃料区均匀化，首先需计算得到共振能区超细群缺陷因子，可采用包含TRISO颗粒的一维球模型计算得到。为推导方便，假设燃料区只填充有一种类型的颗粒，当存在多种类型颗粒时也可采用类似方法推导得到。

包含TRISO颗粒的一维球模型由TRISO颗粒及颗粒外的基质组成。基质半径可由下式计算：

Rm=Rt/F1/3

(3)

式中：Rm为一维球模型的基质半径；Rt为TRISO颗粒半径；F为TRISO颗粒填充率。在颗粒的一维球模型基础上，将边界条件设置为白边边界条件，求解一维超细群中子慢化方程即可得到颗粒各层及基质的通量分布。

用反应率守恒将颗粒的一维球模型进行均匀化，得到的超细群缺陷因子表达式如下：

(4)

(5)

2) 热能区等效均匀化模型

热能区均匀化处理同样采用缺陷因子修正的方法，但由于热能区存在上散射，不能通过求解慢化方程得到缺陷因子。因此本文通过穿透概率及碰撞概率等价得到热能区的缺陷因子。

图2 三维圆柱体模型

穿透概率及碰撞概率等价求解缺陷因子方法采用三维圆柱体模型(图2)。在该模型中，TRISO颗粒位于圆柱中心，圆柱直径是TRISO颗粒直径，中子均匀地从圆柱的底部沿平行于圆柱中心轴方向射入，圆柱高度L可由下式计算得到：

L=4Rt/3F

(6)

通过积分求解可得到中子在该模型中的穿透概率及在TRISO颗粒各层以及基质中的碰撞概率。通过下式即可求得多群缺陷因子[14]：

(7)

(8)

(9)

(10)

采用式(5)修正燃料区各核素的多群截面即可将基质与燃料均匀化。

1.3 等效一维圆柱模型

为将复杂的二维组件问题简化为一维棒问题，基于丹可夫修正因子守恒将燃料组件中的燃料栅元等效为一维圆柱栅元。丹可夫修正因子定义式为：

C=(I0-I)/I0

(11)

式中：C为丹可夫修正因子；I0为孤立系统中进入燃料区的中子数；I为真实问题中进入燃料区的中子数。将整个燃料区假设为黑体，采用中子流方法计算可得到每根燃料棒的丹可夫修正因子。同时，丹可夫修正因子也可通过碰撞概率定义为：

(12)

通过等效过程，可将二维燃料组件等效为多个互相独立的等效一维棒模型，通过求解等效一维棒模型的超细群慢化方程即可得到有效多群截面。

2 数值结果

本文采用的评价核数据库为ENDF/B-Ⅶ.0，能群结构采用WLUP-69，参考解由连续能量的蒙特卡罗程序计算得到。以下计算问题中任意区域的温度为600 K，基质材料为碳化硅，几何与材料参考文献[15]。

2.1 FCM单栅元问题

1) 燃料栅元问题

FCM单栅元燃料问题如图3所示，该问题的几何尺寸和材料组分列于表1，TRISO燃料颗粒的几何尺寸和材料组分列于表2，各材料的核素组成列于表3。TRISO燃料颗粒填充率为30%。

图3 FCM单栅元燃料问题

区域半径或栅距/cm材料燃料0.6252TRISO颗粒+SiC基质气隙0.6337He包壳0.6907FeCrAl慢化剂1.65H2O

表2 TRISO燃料颗粒几何尺寸和材料组分

表3 材料核素组成

图4为FCM单栅元燃料区等效均匀化后共振核素238U和235U的有效自屏吸收截面及其与参考解的相对误差。可看出，有效自屏吸收截面计算结果与参考结果的相对误差较小，238U的有效自屏吸收截面在大部分能群的相对误差小于1%，最大相对误差不超过2.3%；235U的有效自屏吸收截面在大部分能群的相对误差小于1%，最大相对误差不超过1.9%。图5为FCM单栅元燃料问题燃料区热能区修正前后宏观吸收截面误差，可看出，未修正时，燃料区热能区宏观吸收截面误差较大。这是由于在等效均匀化方法中，在燃料区进行了均匀化处理，若热能区不采用缺陷因子进行修正，相当于在热能区采用体积打混均匀化，这样无法精确描述在热能区的TRISO燃料颗粒的自屏效应，会引入较大计算误差。从图5还可看出，采用多群缺陷因子修正能得到较好的热能区自屏截面，能较精确地处理热能区TRISO燃料颗粒的自屏效应。单栅元燃料问题的无限介质增殖因数计算值为1.512 62，参考值为1.513 68，偏差为-106 pcm。计算结果表明，基于超细群方法的FCM燃料的有效多群截面计算方法对于FCM单栅元燃料问题能取得较好的计算结果。

2) 毒物栅元问题

FCM单栅元毒物问题如图6所示，该问题的几何尺寸和材料组分列于表1，TRISO毒物颗粒的几何尺寸和材料组分列于表4，各材料的核素组成列于表3。TRISO毒物颗粒填充率为30%。

图7为FCM单栅元毒物问题燃料区等效均匀化后共振核素238U和235U的有效自屏吸收截面及其相对误差。可看到，有效自屏吸收截面计算值与参考值误差较小，238U的有效自屏吸收截面在大部分能群的相对误差小于1%，最大相对误差不超过1.6%；235U的有效自屏吸收截面在大部分能群的相对误差小于1%，最大相对误差不超过2.5%。图8为FCM单栅元毒物问题燃料区热能区修正前后宏观吸收截面的相对误差，可看出，未修正时，燃料区热能区宏观吸收截面误差较大，最大相对误差超过50%。而采用多群缺陷因子修正能得到较好的热能区自屏截面，热能区自屏截面的相对误差基本能控制在2%以内，能较精确地处理TRISO毒物颗粒热能区的自屏效应。单栅元毒物问题的无限介质增殖因数计算值为0.582 58，参考值为0.583 33，偏差为-75 pcm。计算结果表明，基于超细群方法的FCM燃料的有效多群截面计算方法对于FCM单栅元毒物问题也能取得较好的计算结果。

图4 238U和235U有效自屏吸收截面及相对误差(FCM单栅元燃料问题)

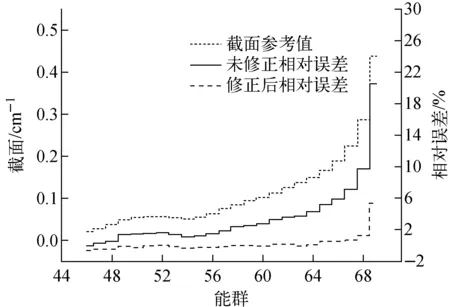
图5 燃料区热能区修正前后宏观吸收截面及相对误差(FCM单栅元燃料问题)

图6 FCM单栅元毒物问题

材料半径/cm材料半径/cm燃料0.0242IPyC0.0380B4C0.0250SiC0.0415缓冲区0.0340OPyC0.0455

图7 238U和235U有效自屏吸收截面及相对误差(FCM单栅元毒物问题)

2.2 FCM组件问题

FCM燃料组件问题如图9所示，该问题的几何尺寸和材料组分取自文献[15]，TRISO燃料颗粒填充率为30%。

图10为FCM组件问题1号栅元的燃料区共振核素238U和235U的有效自屏吸收截面及其误差，可看到，计算结果与参考结果误差较小，238U的有效自屏吸收截面在大部分能群的相对误差小于1%，最大相对误差不超过2.3%；235U的有效自屏吸收截面在大部分能群的相对误差小于1%，最大相对误差不超过2.3%。图11为FCM组件问题1号栅元的燃料区热能区修正前后宏观吸收截面相对误差，可看出，未修正时，燃料区热能区宏观吸收截面误差较大，最大相对误差超过20%。而采用多群缺陷因子修正能得到较好的热能区自屏截面，热能区自屏截面相对误差基本能控制在1%以内，能较精确地处理热能区TRISO颗粒的自屏效应。FCM组件问题的无限介质增殖因数计算值为1.501 398，参考值为1.502 490，偏差为-109 pcm。计算结果表明，基于超细群方法的FCM燃料的有效多群截面计算方法对于FCM组件问题能取得较好的计算结果。

图8 FCM单栅元毒物问题燃料区热能区修正前后宏观吸收截面相对误差

图9 FCM组件问题

图10 238U和235U有效自屏吸收截面及相对误差(FCM组件问题1号栅元)

图11 FCM组件问题1号栅元燃料区热能区修正前后宏观吸收截面相对误差

3 结论

针对FCM燃料的双重非均匀性问题，建立了基于超细群方法的FCM燃料的有效多群截面计算方法，该方法可适用于大规模自屏计算，数值结果表明：

1) 基于超细群方法的FCM燃料的有效多群截面计算方法能很好地处理FCM燃料的双重非均匀效应，得到精确的有效自屏截面；

2) 由于TRISO颗粒在热能区有很强的自屏效应，尤其在TRISO毒物颗粒中，自屏效应更强，因此必须对FCM燃料的热能区进行自屏计算，计算结果表明，采用缺陷因子能很好地处理FCM燃料的热能区自屏效应。