反应堆内熔融物冷却的三维数值模拟研究

薛 峰，袁明豪，张 建，陈秋炀

(苏州热工研究院有限公司 核安全与运行技术中心，江苏 苏州 215004)

核电厂发生严重事故，特别是在发生高压熔堆事故时，会对安全壳的完整性造成极大威胁，因此如何保持压力容器完整性，将堆芯熔融物保持在压力容器内是严重事故缓解措施研究的重点。堆芯熔融物压力容器内滞留(IVR)是一种重要的严重事故管理措施，主要应用于先进的轻水堆核电站，其主要目的为通过压力容器外部的冷却降低内部熔融物的温度，从而保持压力容器的完整性，使熔融物滞留在压力容器内部，避免放射性物质的释放。

国内外对IVR进行了大量研究和应用。芬兰Lovvisa核电厂首次在VVER-440反应堆上应用了堆腔注水系统[1]。西屋的AP600和AP1000[2]以及韩国的APR1400[3]在设计中也考虑了堆腔注水概念，开展了相关的实验和计算验证其安全性。中国自主设计的华龙一号中已应用IVR技术[4]，以提高核电厂应对严重事故的能力。

堆芯发生熔化后，熔融物坍塌至压力容器下封头形成熔池，熔池自身的特性和结构对于壁面传热和下封头的完整性具有重要的影响。杨晓等[5]开发了MOPOL程序并对IVR有效性评价中的不确定性进行了分析。陈星等[6]和傅孝良[7]分别使用MOPOL程序对CPR1000堆型的IVR有效性进行了评价。Zhang等[8-9]开发了IVR分析的软件IVRASA并对AP1000的不同工况进行了评价分析，另外还通过实验装置COPRA开展了下封头内堆芯熔融物换热特性的实验研究。曹臻等[10]开发了三层熔池模型分析程序SPIRE并进行了验证。本文基于日本应用能源研究所(IAE)开发的SAMPSON程序，对压力容器内熔融物扩展和冷却分析(DCA)模块进行改进开发，并与实验结果进行对比。

1 模型及基本方程

1.1 熔融物扩展冷却模型

SAMPSON程序DCA模块的瞬态计算流程如图1所示。

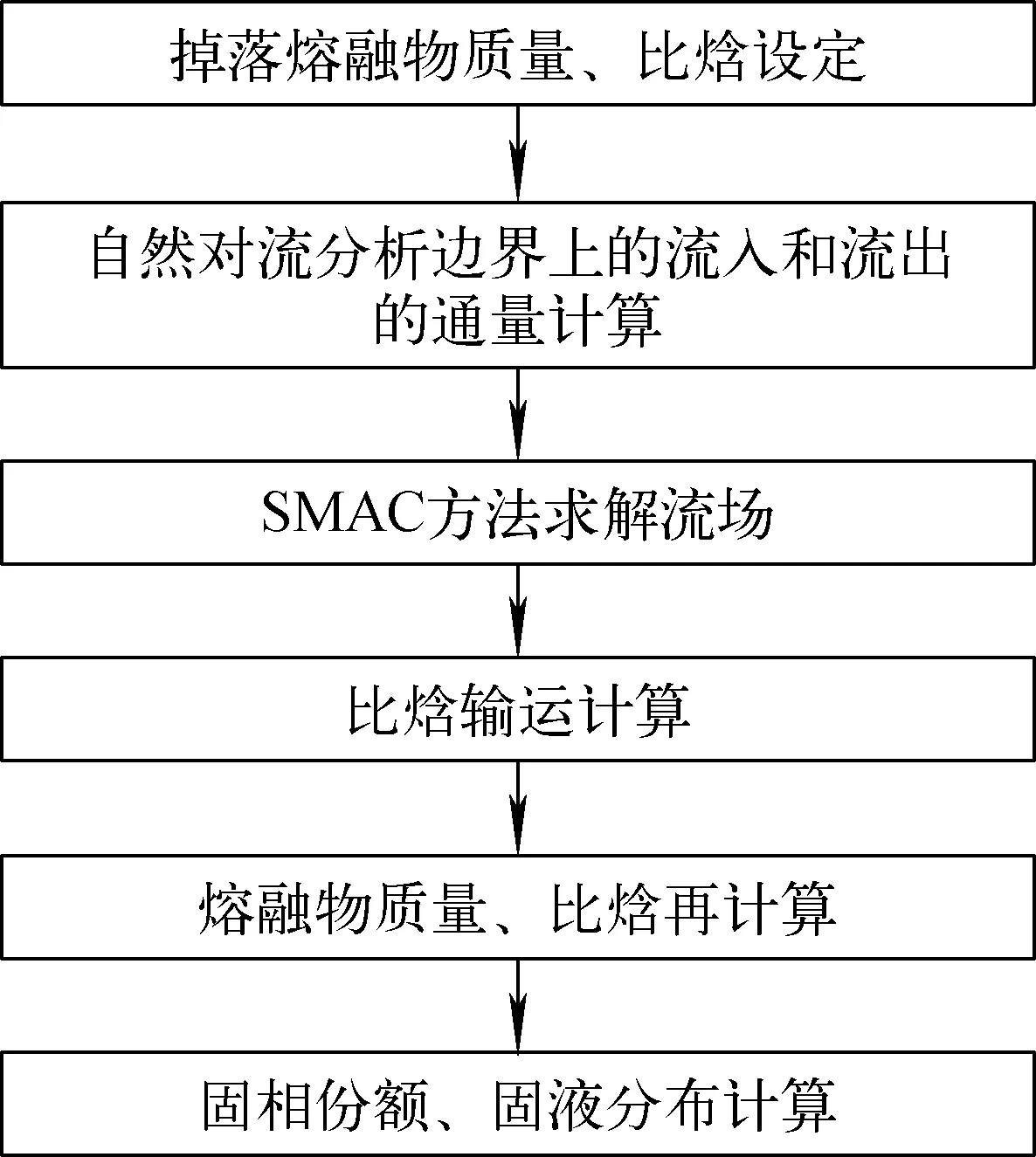
图1 DCA模块的瞬态计算流程

熔融物在压力容器下腔室内的扩展和冷却模型如图2所示，该模型的分析方法如图3所示。连续相的融熔物被视为牛顿流体，流动和传热采用N-S方程进行分析。网格被赋予两种属性：自然对流分析网格及液相自由表面网格，以模拟熔融物的扩展、熔化和凝固的作用。自然对流分析网格是指充满融熔物、硬壳的网格，采用SMAC(simplified marker and cell)方法进行流动计算。液相自由表面网格是指没有被充满的网格，采用高度函数来计算流动。

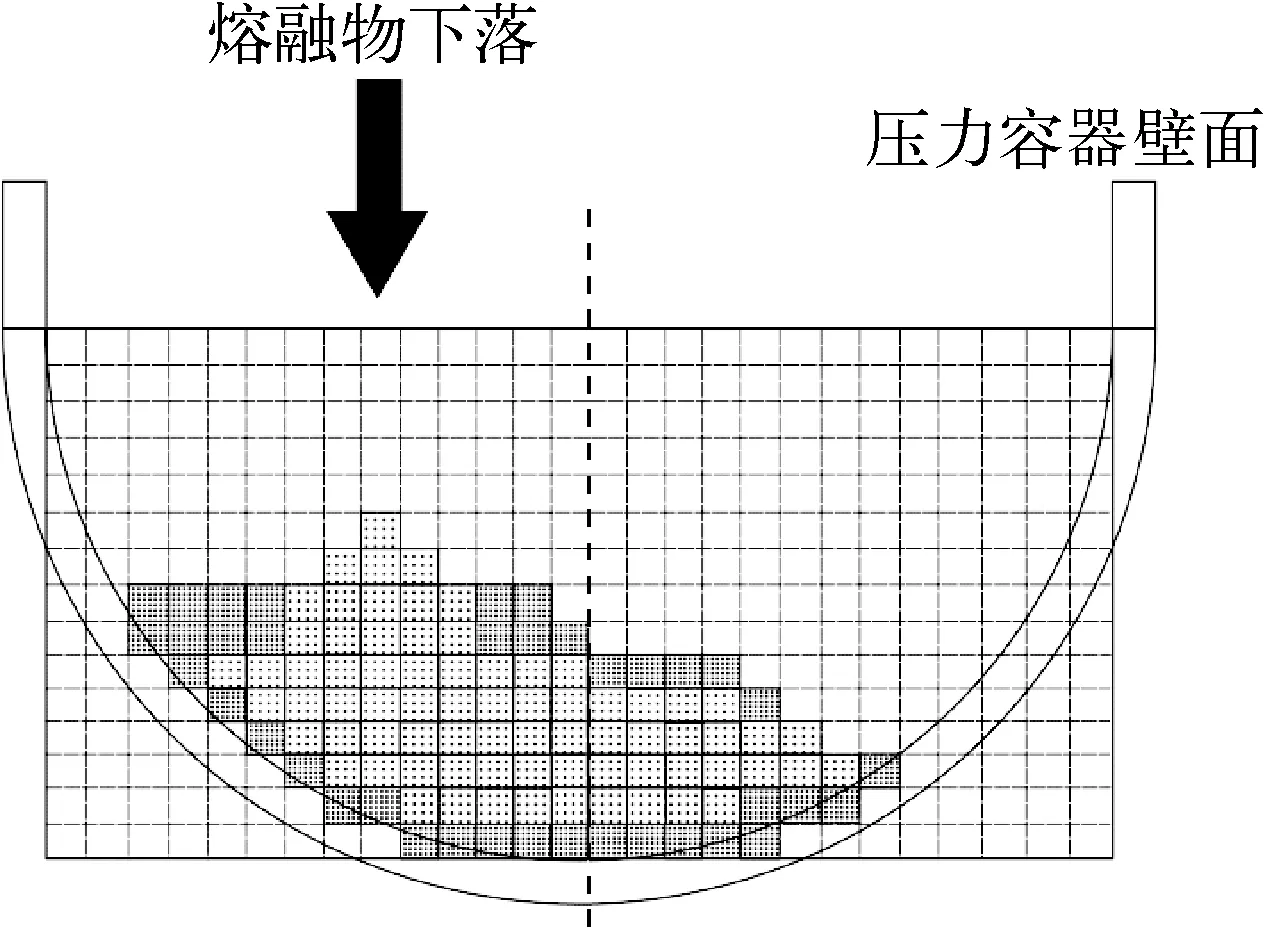
图2 熔融物在压力容器下腔室内的扩展和冷却模型

本文分析中作如下假设：1) 连续相融熔物的扩展是由重力主导的，因此不考虑融熔物向空气散布及其中涉及的气相；2) 硬壳的迁移被限制在竖直方向。由假设1可知，从自然对流分析网格流到分析边界外面网格的融熔物会聚集在液相自由表面网格的下部。

图3 熔融物扩展和冷却模型的分析方法

1.2 基本方程

1) 自然对流分析网格的基本方程

DCA模块中关于自然对流分析网格内的扩展和自然对流行为的基本方程包括质量守恒、动量守恒和能量守恒方程。

质量守恒方程为：

(1)

动量守恒方程为：

(2)

(3)

(4)

其中：u、v、w是流体在t时刻，在坐标点(x、y、z)处的速度分量；ρ为密度；p为压力；μ为动力黏度；g为重力加速度；H为高度；K为浮升力项，采用Boussinesq假设。

(5)

能量守恒方程为：

(6)

其中：e为比焓；λ为导热系数；T为温度；Q为热源。

熔融物的熔化、凝固状态，由以下公式计算每个网格的温度和凝固份额来确定，其中比焓由能量守恒方程得到。

(7)

其中：cs和cp分别为固态和液态时的比热容；Tl为熔化温度；el为熔化比焓；es为凝固比焓；b为凝固份额，完全凝固时，b=1，完全熔化时，b=0。当b超过某一值时，流动将停止。对于铁和非铁合金，b在0.5～0.7范围内。

当b超过流动限值时，假设连续相融熔物凝固，流体速度被置为0。通过在每个计算步长的压力计算中应用该边界条件，来实现流动计算中对固液界面迁移的处理。对于能量计算，由于可计算凝固网格的导热，固相和液相被当作连续体。

2) 液相自由表面网格的基本方程

根据假设，连续相融熔物的迁移受到重力和壁面的限制。对于液位参考平面不变的情况，使用高度函数来追踪液相表面的位置。xy平面作为参考平面，z方向表示距离参考平面的液位。液体高度H的运动方程为：

(8)

1.3 数值算法

DCA模块的流场计算采用SMAC方法。首先求解自然对流分析边界内的质量守恒和动量守恒方程，得到连续相融熔物的流速，然后使用该流体速度求解能量方程。

网格采用固定交错网格，压力和温度定义在网格的中心，流速定义在网格的界面上，如图4所示。图4中，i、j、k分别为x、y、z方向上的网格编号。

2 程序开发

2.1 两层熔池模型

熔池在压力容器下封头达到最终稳定分层结构之前要经历的中间过程仍存在较大的不确定性，国内外[7,11]提出了不同的熔池分层结构，本文采用目前最具有代表性的两层熔池模型。熔池底层为密度较大的氧化池，包含UO2、ZrO2等氧化物和内热源。此外，氧化池与温度较低的下封头和上部金属层接触，冷凝成一层硬壳。由于硬壳顶部覆盖的金属层温度与下封头容器壁温度不同，故氧化池上、下硬壳厚度并不一致。

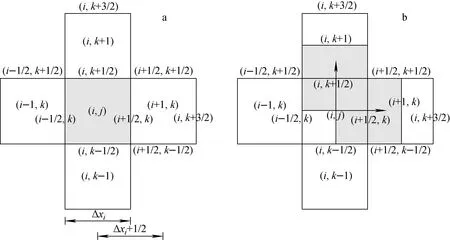
a——压力、焓计算二维网格；b——速度计算二维网格图4 交错网格示意图

熔池上层由密度相对较小的金属层构成，包含熔化的不锈钢和未被氧化的锆等金属物。由于金属层质量与氧化池质量相比往往很小，故其厚度较薄。

无论采用何种熔池结构，当堆芯熔化并塌落至下封头形成分层熔池后，下封头壁面受热的热流密度沿其轴向是非均匀分布的。熔池上层的金属层由于质量小、厚度薄，造成其热流密度很大，形成热聚集效应。若此处的热流密度超过临界热流密度(CHF)，会对压力容器的完整性构成巨大威胁。

在SAMPSON程序的DCA模块中，假设熔融物的成分是均匀的，无法模拟熔融物中的金属层的聚焦作用。为此本文对该模块的下封头内熔融物冷却模型进行改进，增加氧化池与金属分层模型，如图5所示。

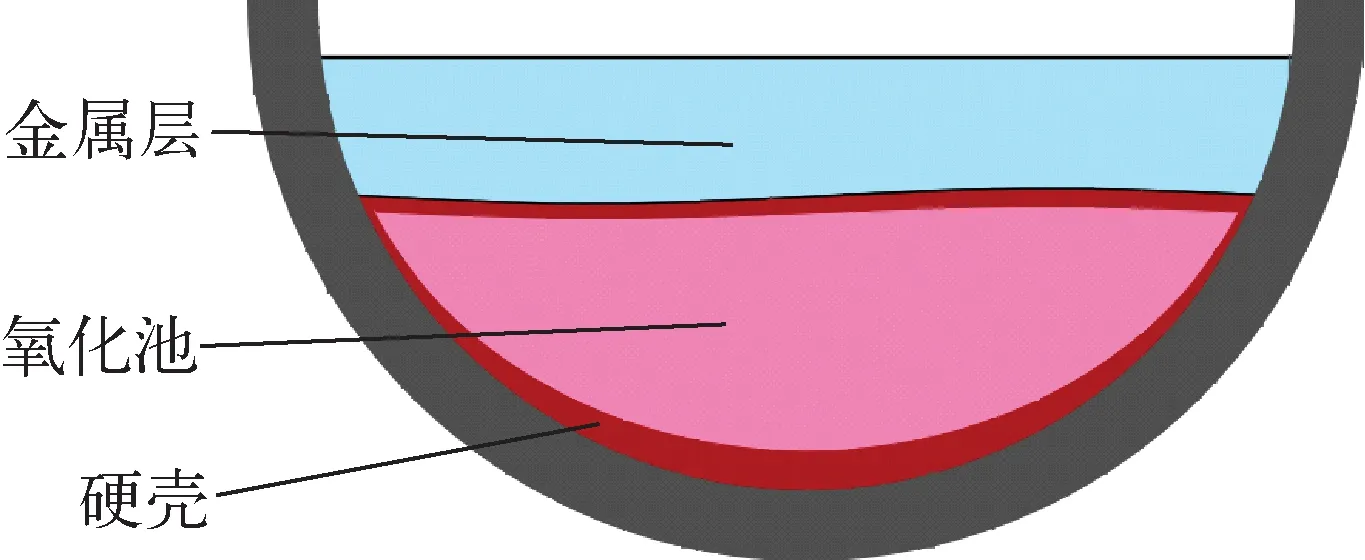
图5 氧化池与金属分层模型

在熔融物扩展和自然对流模拟过程中，假设金属与氧化池分层布置，各自的厚度(体积)取决于掉落到下封头内的熔融物的质量和组分。

金属层与氧化池的物性分别计算，采用物性包MATPRO[12]。其中金属的主要成分为铁和锆，锆金属的密度使用CDEN函数计算：

ρ=ρ0exp(-εx)exp(-εy)exp(-εz)

(9)

其中：ρ0为参考密度，取温度为300 K时的值6.55×103kg/m3；εx、εy、εz为任意正交坐标系下的应变，由CTHEXP函数计算。因为热应变小于1，因此式(9)可近似为：

ρ=ρ0(1-εx-εy-εz)

(10)

锆金属的导热系数λz使用CTHCON函数计算，仅考虑温度为决定因素，当温度低于2 098 K时，其计算公式为：

λz=7.51+2.09×10-2T+

1.45×10-5T2+7.67×10-9T3

(11)

锆金属导热系数的实验数据及拟合曲线如图6所示。

钢的密度使用SDEN函数计算，参考密度取温度为300 K时的值7.9×103kg/m3。

钢的导热系数使用STHCON函数计算，其公式为：

λs=7.58+0.189T300 K≤T<1 671 K

λs=610.93+0.342T

1 671 K≤T<1 727 K

λs=20 W/(cm·K)T≥1 727 K

(12)

在本文计算中仅考虑钢完全熔化的工况，因此取其导热系数为20 W/(cm·K)。

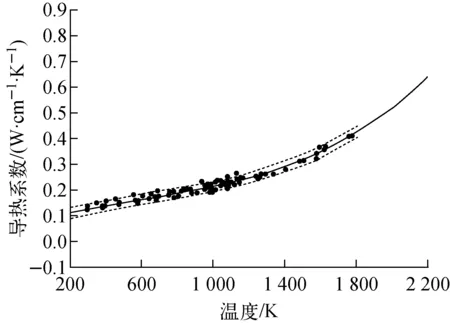
图6 锆金属的导热系数

金属层与氧化池分界面处的物性采用插值计算，图7给出了分层界面附近的导热系数插值示意图。

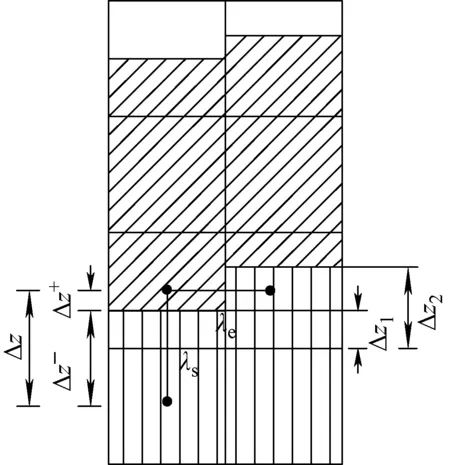
图7 分层界面附近的导热系数插值

假设氧化池的导热系数为λo，金属层的导热系数为λm，界面附近的导热系数可采用下式计算：

(13)

λu=λof+λm(1-f)

(14)

其中：Δz为网格中心距；Δz-、Δz+、Δz1、Δz2的含义如图7所示；λd和λu为包含分界面的网格单元的导热系数，分别对应分界面位于网格中心的下方和上方(图7)两种情况；f为插值系数。

2.2 压力容器外表面传热

压力容器的传热模型和网格划分如图8所示，其中，qin为来自熔融物的热流，qcond为导热热流，qout为到安全壳大气的热流。通过求解三维导热方程(式(15))得到压力容器的温度分布。

图8 压力容器壁面网格和传热模型

e=ct+(1-b)Hsl

(15)

其中：λ为导热系数；Q为传入热量；c为比热容；Hsl为熔化潜热。

压力容器下封头外表面向堆腔的传热包含向空气和水两部分的传热，其计算公式如下：

qrpv=hgas(1-α)Arpv(T(θ)-Tgas)+

hpoolαArpv(T(θ)-Tpool)

(16)

其中：qrpv为下封头外表面向堆腔的传热；hgas和hpool分别为下封头到堆腔空气和水的对流传热系数；α为下封头被水淹没的面积份额；Arpv为下封头表面积；T(θ)为下封头外表面在角度θ处的温度，其中θ=0°表示下封头底部；Tgas和Tpool分别为堆腔内空气和水的温度。

对于外表面与空气的传热，hgas使用大空间自然对流换热实验关联式(式(17))计算，此关联式在工程中广泛使用。

Nu=C(GrPr)n

(17)

其中：Gr为格拉晓夫准则数；Nu为努塞尔数；Pr为普朗特数；h为对流换热系数；L为传热面的几何特征长度；系数C和指数n根据流体处于层流或湍流取不同的值。

外表面与水的传热在下封头外表面温度未达到堆腔中水的饱和温度时，使用式(16)计算自然对流换热。当下封头外表面温度大于饱和温度时，则考虑沸腾传热。

2.3 网格前处理程序

由于下封头内的熔融物采用三维直角坐标网格，而下封头本身采用三维曲线坐标网格(图9)，所以必须预先确定两套网格之间交界面的几何参数。SAMPSON程序的DCA模块本身不具备产生这些几何参数的能力，这些参数需人工计算产生，当网格数量较大时，产生这些参数的工作量很大，无法确保其可靠性。因此，为便于快速准确地得到两套网格间的几何参数，以及互相映射的关系，本文开发了前处理程序来自动产生这些参数。

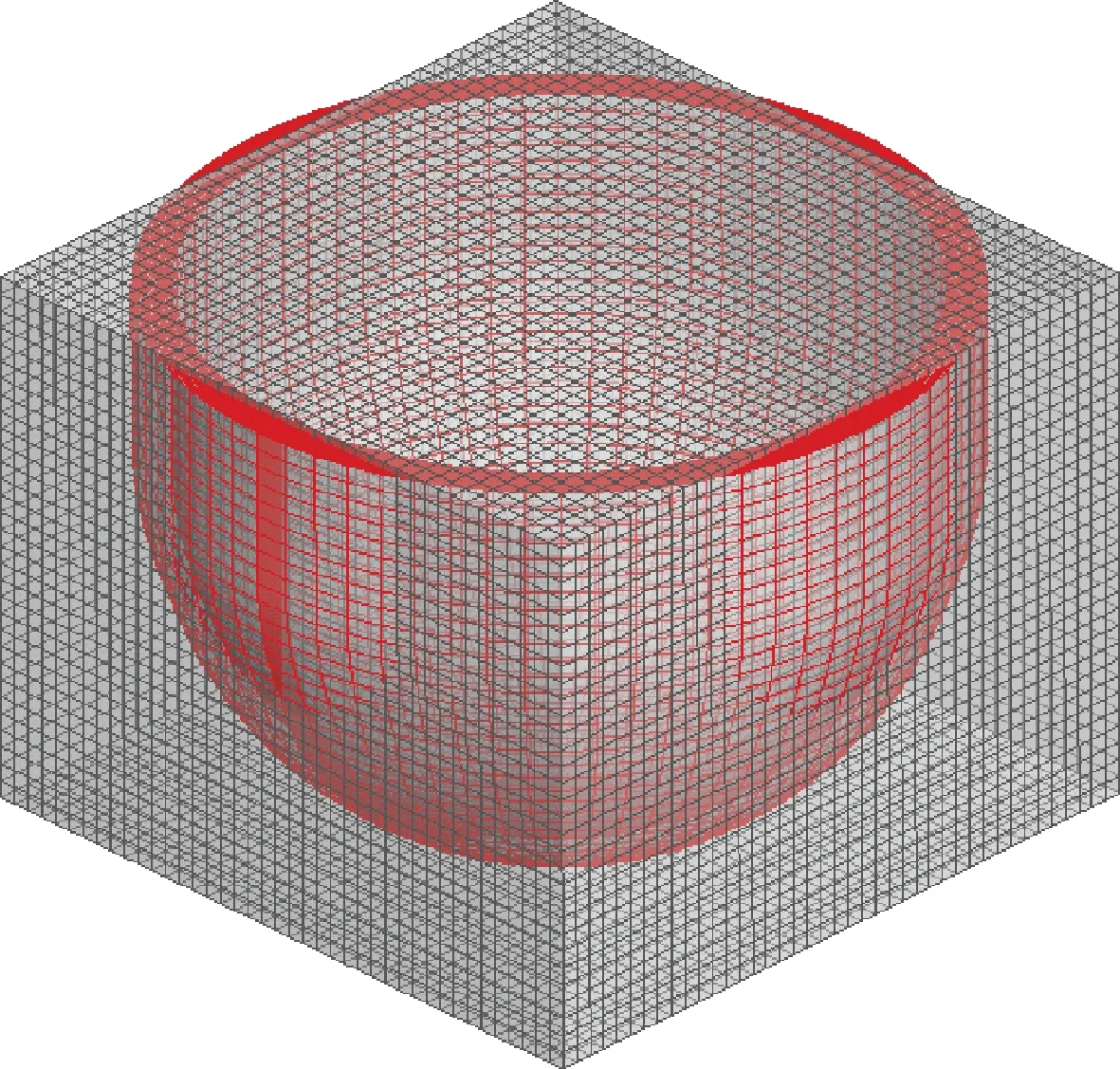
图9 压力容器网格(红色)和熔融物网格(灰色)

该前处理程序首先根据设定的压力容器下封头节点布置产生网格，再将下封头网格的任一内表面分为M×N个极小的微面积，根据每一微面积的坐标判断其所处的熔融物三维直角坐标网格单元。通过对M×N个微面积进行累加，即可确定该下封头网格内表面所映射的熔融物三维直角坐标网格(可对应多个)以及相互接触的面积。对下封头内表面所有网格循环计算后，就可得到关于熔融物网格与压力容器网格交界面的所有几何参数。

3 验证计算

3.1 计算模型与假设

为对改进后的DCA模块进行验证，本文选取AP1000核电机组建立模型进行计算分析。AP1000核电机组下封头的尺寸根据文献[11]选取。压力容器下封头网格与熔融物网格的敏感性分析如图10所示，最终压力容器下封头选取42×72×20个网格，壁面方向的网格加密是为了尽可能详细模拟下封头壁面的减薄效应。下封头内部的熔融物网格为42×42×32的直角坐标网格。熔融物网格与压力容器网格交界面的映射关系由前处理程序自动产生。

文献[11]采用拉丁超立方体抽样(LHS)技术对堆芯熔融物材料分布和余热进行计算，给出了基准工况假设，本文采用此工况进行计算，基准工况参数取值列于表1。

堆芯熔融物逐步塌落至下封头中形成熔池。先期坍塌的熔融物在下封头中经历一段时间后形成具有氧化池和金属层的两层结构，随后熔化的熔融物经历一段时间后分解并溶入相应各层，最终熔池稳定于两层结构。因此熔融物落下的瞬态过程对下封头失效的影响是可忽略的。

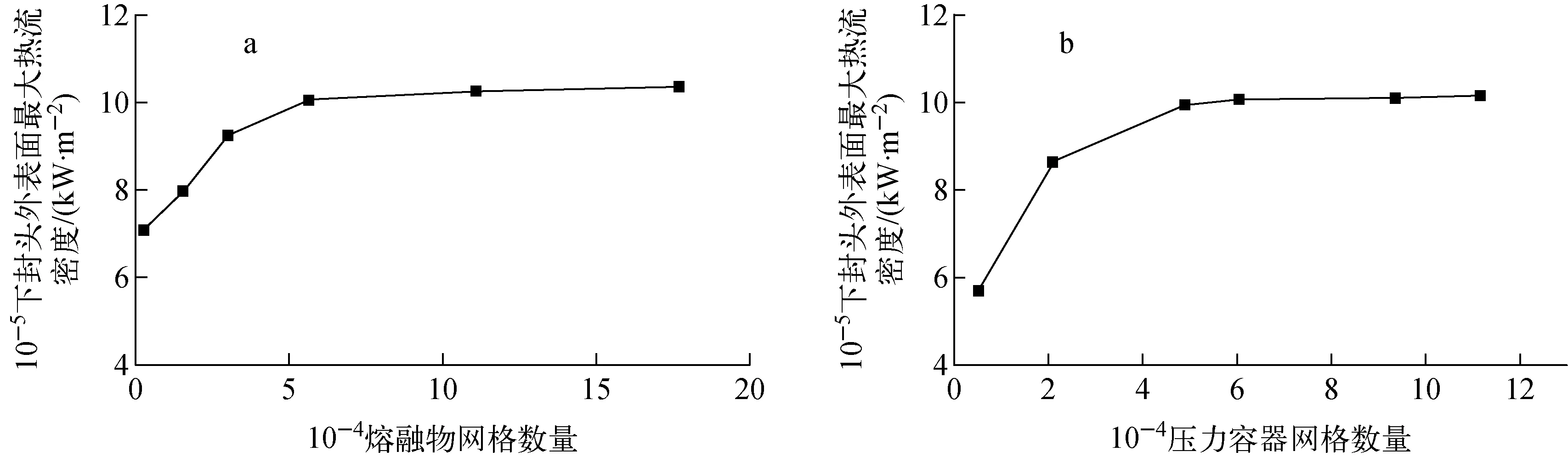
图10 熔融物(a)与压力容器(b)的网格敏感性分析

表1 基准工况的参数

在使用本文程序进行计算时，对熔融物落下的瞬态做了简单化处理。假设表1中的熔融物以一定流量快速落入下封头，当这些熔融物全部进入下封头后，氧化物与金属开始分层。程序的收敛准则为熔融物产生的衰变余热与从金属层上部辐射传出的热量及通过下封头外壁面传出的热量达到平衡(图8)，热平衡公式为：

Q衰变热=Q金属层辐射+Q壁面热导出

(18)

当金属熔池周围的壁面温度超过压力容器壁面的熔点温度(假设为1 700 K)时，压力容器下封头壁面发生烧蚀。

3.2 计算结果

图11示出中心对称截面上熔融物的流场和温度分布。当下封头的熔池达到稳态后，上层的金属层温度约为2 020 K，下层的熔融物温度达到3 000 K。氧化池的热量通过金属层向上和侧面传递。金属层向上通过辐射传热的热量较小，向容器壁的侧向传热通道较为畅通，大部分热量通过金属层侧面对流传导给压力容器壁面。金属层的导热性能远高于氧化池，能快速导出热量，因此其温度要低于氧化池。

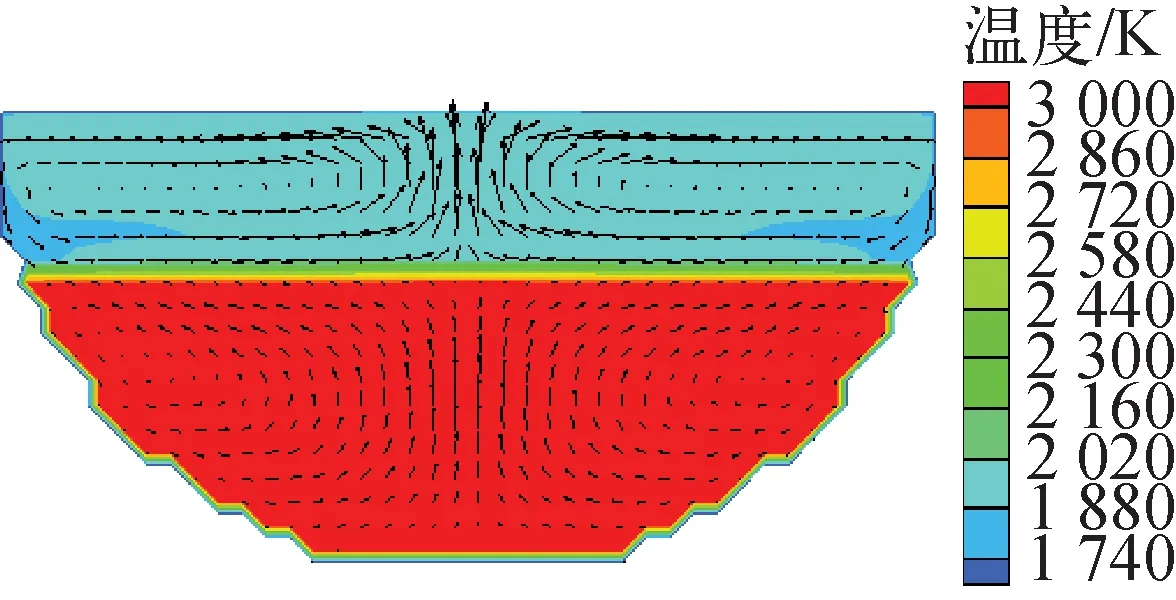
图11 中心截面上熔融物的流场和温度分布

由图11的流场可看出，氧化池同时被压力容器壁面和上层金属层冷却，故其自然对流会形成两个对称的涡结构，同样的压力容器壁面会较大程度地冷却金属层，金属层也会形成两个对称的涡结构。

图12示出压力容器下封头壁面和厚度方向的温度分布。由于金属层会向压力容器壁面传递较多的热量，与金属层接触的壁面有较高的温度且会达到其假设熔点1 700 K，部分厚度的壁面会被熔化，而氧化池接触的压力容器壁面温度分布较为均匀。故可看出金属层的特性会对压力容器的失效起着决定作用。

图13示出压力容器下封头外壁面的热流密度和被熔化的厚度。由图13可知，在金属层与下封头接触之处，下封头厚度急剧减薄，此处的热流密度急剧升高，金属层的聚焦作用较为明显。将图13的结果与文献[11]的进行比较，在金属层与下封头接触处的热流密度两者较接近，但氧化池的热流密度分布两者有较明显区别。本文计算得到的氧化池的热流密度随角度的变化较为平缓，文献[11]给出的氧化池的热流密度在角度大于30°时有显著上升。这是由于文献[11]在计算时使用了文献[13]给出的关系式以及文献[2]给出的mini-ACOPO实验数据。

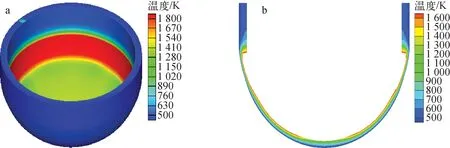
图12 压力容器下封头壁面(a)和厚度方向(b)的温度分布

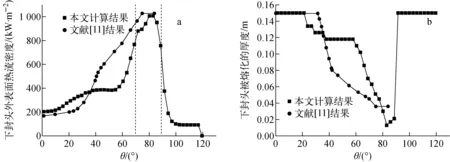
图13 压力容器下封头外表面的热流密度(a)和被熔化的厚度(b)

在mini-ACOPO实验中，熔融物的上表面未考虑金属层冷却，而在实际的堆内熔融物冷却滞留分析中，压力容器下封头内的氧化池的上方覆盖了一层较低温度的金属层，氧化池上方存在较强换热，与本文计算工况不符，故本文参考BALI实验[14]结果进行对比分析。

BALI实验对氧化池上方金属层的冷却作用进行了研究，实验结果表明，存在顶部冷却时，60°以上区域的热流密度变化较均匀。本文重新计算了BALI实验工况，并对氧化池的热流密度进行无量纲化处理，将之与实验结果的拟合曲线进行比较，如图14所示，两者吻合较好。因此，由于顶部金属层的冷却使得靠近金属层的氧化池的壁面换热更加均匀，而远离金属层部分的换热会随角度有迅速变化的趋势。

4 结论

本文对日本应用能源研究所(IAE)开发的SAMPSON程序进行二次开发，在DCA模块中增加了下封头内堆芯熔融物金属和氧化物分层模型，完善了压力容器外表面传热模型，并独立开发了直角坐标和曲面坐标网格前处理程序。

图14 下封头外表面热流密度与BALI实验结果对比

为验证改进的DCA模块，选取AP1000核电机组建立下封头模型进行计算分析，并与文献和实验结果进行对比，结果吻合较好，表明改进的DCA模块可有效地模拟下封头内堆芯熔融物的流动和冷却特性，并用于堆内熔融物冷却滞留的分析评价。