基于正向蒙特卡罗计算的自动源偏倚方法在屏蔽计算中的应用
邱有恒,史 涛
(1.北京应用物理与计算数学研究所,北京 100094;2.上海核工程研究设计院有限公司,上海 200233)
屏蔽计算问题是蒙特卡罗方法的难点问题。以反应堆屏蔽计算为例,仅有少量处于堆芯外围组件的高能中子能到达屏蔽层外,若采用无偏抽样,大量的计算时间用于模拟无用的源粒子,计算效率很低。
偏倚抽样是提高蒙特卡罗模拟计算效率最核心的思想,包括3类偏倚方案[1]:源偏倚、输运偏倚(如赌与分裂、指数变换)、碰撞偏倚(如离散角度偏倚、强迫碰撞、隐俘获等)。
在学术界和核工程领域,专家和学者发展了大量的降低方差技巧,包括指数变换法、分层抽样法、轮盘赌和分裂方法、统计估计法、权重窗等[2-4],但这些方法主要集中在输运和碰撞偏倚。MCNP程序[5]是通用的粒子输运蒙特卡罗程序,配备了多种降低方差技巧,但同样缺乏自动源偏倚功能。而对于反应堆屏蔽这样的问题,仅采用输运偏倚和碰撞偏倚通常是不够的,必须要配合源偏倚。虽然用户也可利用个人经验进行源偏倚,但缺乏科学量化依据且难以处理复杂源。
对于自动源偏倚抽样比较有代表性的方法是CADIS方法[6],该方法是利用确定论方法开展伴随输运,利用伴随通量实现源偏倚抽样。JMCT软件也配备了基于伴随通量的自动源偏倚抽样技巧[7],该软件是用蒙特卡罗方法进行伴随输运,采用虚拟MESH方法存放偏倚参数,适用于各种复杂源描述。该软件在反应堆屏蔽计算中取得了很好的效果。
事实上,利用正向蒙特卡罗计算通量可产生重要性函数,这方面的优秀代表是MCNP程序的权窗发生器。本文在MCNP程序基础上,开发基于正向蒙特卡罗计算自动源偏倚抽样功能,以实现与权窗自洽耦合。
1 理论与方法
1.1 偏倚抽样基本理论
考虑如下数学期望的计算:

(1)
其中:f(x)为分布函数;g(x)为响应函数,当从f(x)抽样困难或计算效率很低时,可考虑如下形式的计算:
(2)
其中:f′(x)为偏倚分布函数;f(x)/f′(x)为纠偏因子。正确使用偏倚抽样能保证数学期望不变,计算效率提高。
1.2 权窗与权窗发生器
权窗是诸多降低方差技巧中的一种。权窗可替换几何重要性和能量分裂来指定空间和能量重要性函数,也可提供时间关联的重要性函数,较几何重要性函数的信息量更大。
权窗有3个参数,分别是权窗下限(WWL)、权窗上限(WWU)、存活粒子权重(WS)。通过权窗游戏,可将粒子权重分布控制在合理的范围内。假定某相空间粒子权重W落在以下3个区间,根据权窗规则,粒子权重将作相应调整。
1)W 2) WWL 3)W>WWU,对粒子实施分裂游戏。首先分裂成[W/WS]个子粒子([ ]表示取整),再以概率W/WS-[W/WS]产生另一个子粒子,它们的权重均为WS。 MCNP程序有权窗发生器功能,可自动生成各相空间经过优化后的权窗系数,包含以下两步。 1) 统计各相空间重要性。对于栅元i的第g群粒子,其重要性等于由该相空间发出的所有径迹对探测器的贡献除以进入该相空间的所有粒子数,用IMP(r,E)表示。 2) 由重要性转换为权窗下限。选定1个参考栅元(通常为源所在栅元),确定参考栅元最大重要性的相空间的权窗下限wg,wg由用户指定,默认值为源粒子平均权重的1/2。其他所有相空间权窗下限反比于其自身的重要性。 (3) 式中:max(IMP(rref,E))为参考栅元不同能群源粒子对探测器贡献的最大值;wg默认为0.5,因此,对于源区,权窗下限最小值为0.5。 本文采用与JMCT和CADIS方法同样的思想产生源偏倚函数,即某相空间偏倚概率正比于重要性函数与无偏概率乘积,只是此处用正向蒙特卡罗计算过程产生的重要性函数替换伴随通量。 (4) 其中:S(r,E)为无偏倚的抽样概率;Sb(r,E)为偏倚抽样概率。源粒子权重修正: (5) 修正后的源粒子权重可能很大或很小,必须采用与之匹配的权窗系数,否则将发生大量的赌与分裂,从而失去源偏倚的意义。权窗下限为: (6) MCNP程序的Cu默认值为5,即源区权窗下限为纠偏后权重的1/3,确保偏倚抽样后纠偏后的源粒子不会发生赌;由于MCNP程序默认的权窗上限是下限的5倍,因此也不会发生分裂。对于非源区,权窗下限直接反比于重要性。 如图1所示,模型为150 cm高的圆柱,圆柱内为铅,源点位于圆柱底部半径25 cm圆盘内,源中子能谱为裂变谱,测点坐标(0,0,155 cm)。 图1 铅屏蔽模型 在相同的计算机上,不同模型计算结果列于表1,在下文的叙述中,将不采用重要性的方法称为方法1,将采用几何重要性的方法称为方法2,将采用MCNP模式的权窗方法称为方法3,将本文方法称为方法4。采用方法1计算时,可同时产生方法3和方法4的参数。其中计算优度FOM定义为统计误差平方与计算时间乘积的倒数,显然,FOM越大表明计算效率越高,表中FOM1表示单次计算的FOM,FOM2表示累加了产生权窗参数所用时间的FOM。 表1 不同方法的计算结果与效率比较 从表1可见,若采用方法1,模拟8×107样本,统计误差较大,达0.106 3;采用方法2,同样8×107样本,统计误差很小,仅0.005 7,结果已收敛,但计算时间超长,约21 h,FOM较无重要性的高约30倍。 采用方法3,样本数为2×107的情况下,统计误差仅0.003 9,低于几何重要性函数,计算结果与几何重要性几乎完全相同,FOM远高于几何重要性。 采用方法4,计算结果与几何重要性结果几乎完全一致,计算统计误差较方法3的更小,但FOM更大,尤其FOM2较方法3约提高2倍。 图2为某商用压水堆一次屏蔽计算模型。实验测点位于30°方向上第6根辐照监督管中平面和顶端。中平面测点的数值模拟相对容易,与测试结果也符合较好,但顶端测点的数值模拟收敛很慢,采用几何重要性方法模拟2×109样本(MCNP上限)所得结果与测试值相差较大。为此,本文采用基于正向蒙特卡罗计算重要性函数的自动源偏倚与权窗耦合技巧,计算结果与测试值符合较好,计算精度和效率远高于几何重要性方法。 图2 某压水堆一次屏蔽计算模型 图3 中平面处源中子分布 图3示出了堆芯中平面处pin_by_pin源中子分布。图4示出了中平面测点的源中子偏倚抽样概率,从图中可见,仅少量外围组件有抽样,绝大部分组件抽样概率为0。图5为顶端测点的源中子抽样概率分布,与图4现象类似。 图4 中平面测点的源中子偏倚抽样概率 图5 堆芯顶端测点的源中子偏倚抽样概率 图6 堆芯源中子抽样能谱比较 图6示出了源中子能量偏倚概率,对于中平面测点,0.4 MeV以下源中子抽样概率为0;对于顶部测点,1 MeV以下源中子抽样概率为0。通过能量偏倚抽样,使更多高能源中子参与输运,提高计算效率。 图7示出了堆芯轴向抽样概率比较。无偏抽样时,堆芯中部抽样概率高,顶端和低端抽样概率低;针对中平面测点的偏倚抽样主要集中在z为-60~40 cm之间,其余部分抽样概率几乎为0;针对顶端的偏倚抽样集中在z大于80 cm的部分。 图7 堆芯z轴抽样概率比较 表2列出了顶端测点通量密度结果比较(中平面测点难度较小,未列出)。若只采用几何重要性,即便样本数达到2×109,各能群中子通量密度均明显小于测试值,其原因是源中子高能段抽样不够;采用源偏倚与权窗耦合技巧后,计算效率大幅提高,只需2×107样本,在单机上耗时约0.5 h,各能群中子通量密度统计误差均在2%以内,收敛状况良好,中子通量密度计算值与实验值相对误差均小于20%,达到工程设计的要求,计算优度FOM为93,较只采用几何重要性的计算优度0.68提高2个量级。 表2 辐照监督管顶端测点通量密度比较 本文利用MCNP程序的权窗发生器产生的重要性函数,生成了自动源偏倚以及与之耦合的权窗系数,在屏蔽计算中取得了很好的效果。本文方法中偏倚参数既可采用栅元模式也可采用虚拟MESH模式,与MCNP的权窗功能完全兼容,使用方便。1.3 基于正向蒙特卡罗计算重要性的源偏倚抽样方法
2 数值算例
2.1 铅屏蔽模型
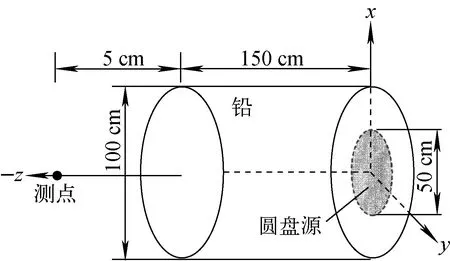

2.2 反应堆屏蔽计算算例



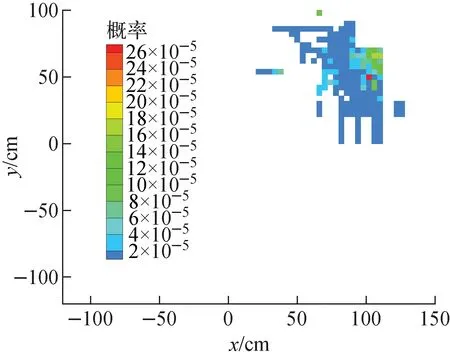
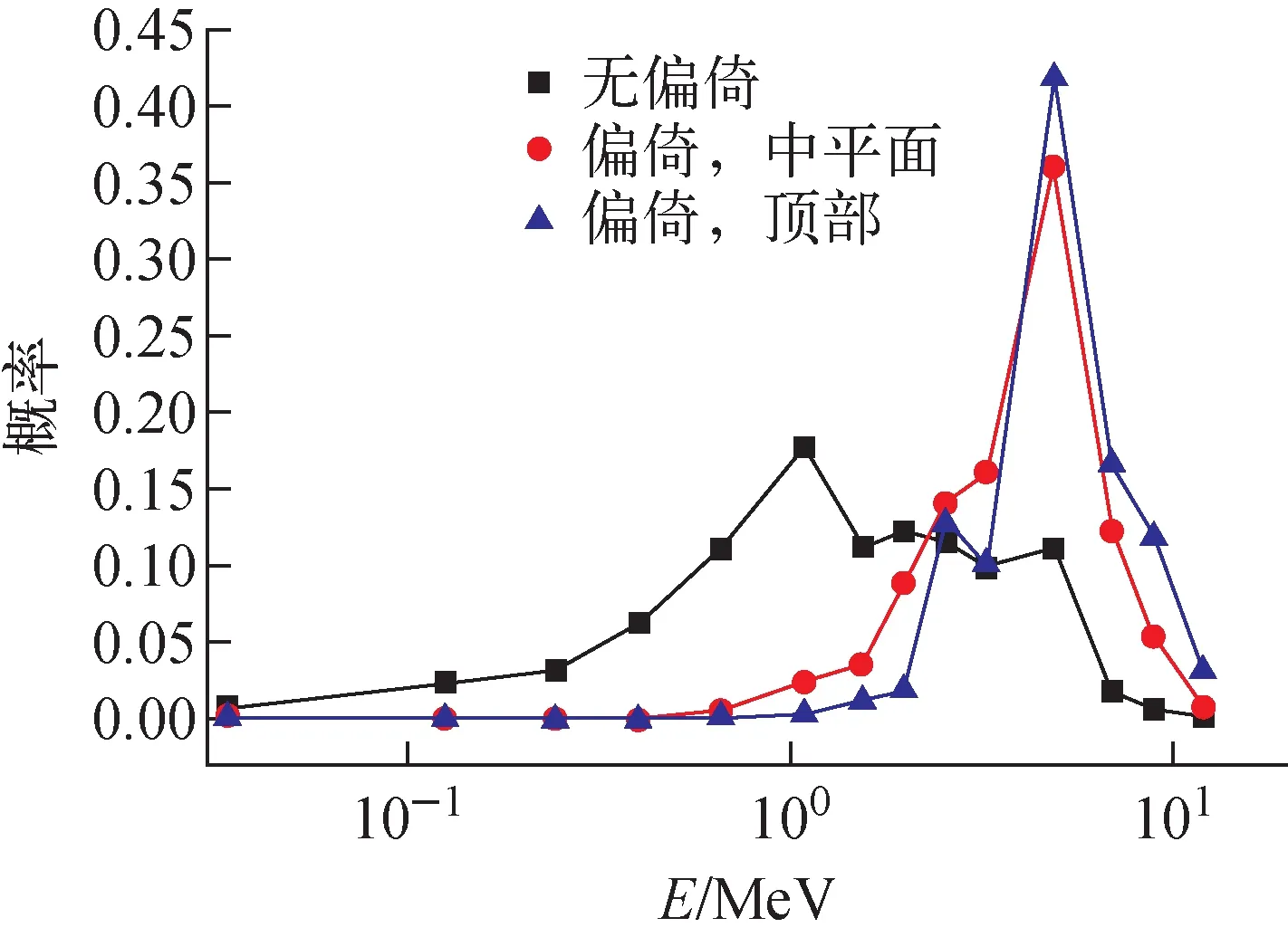
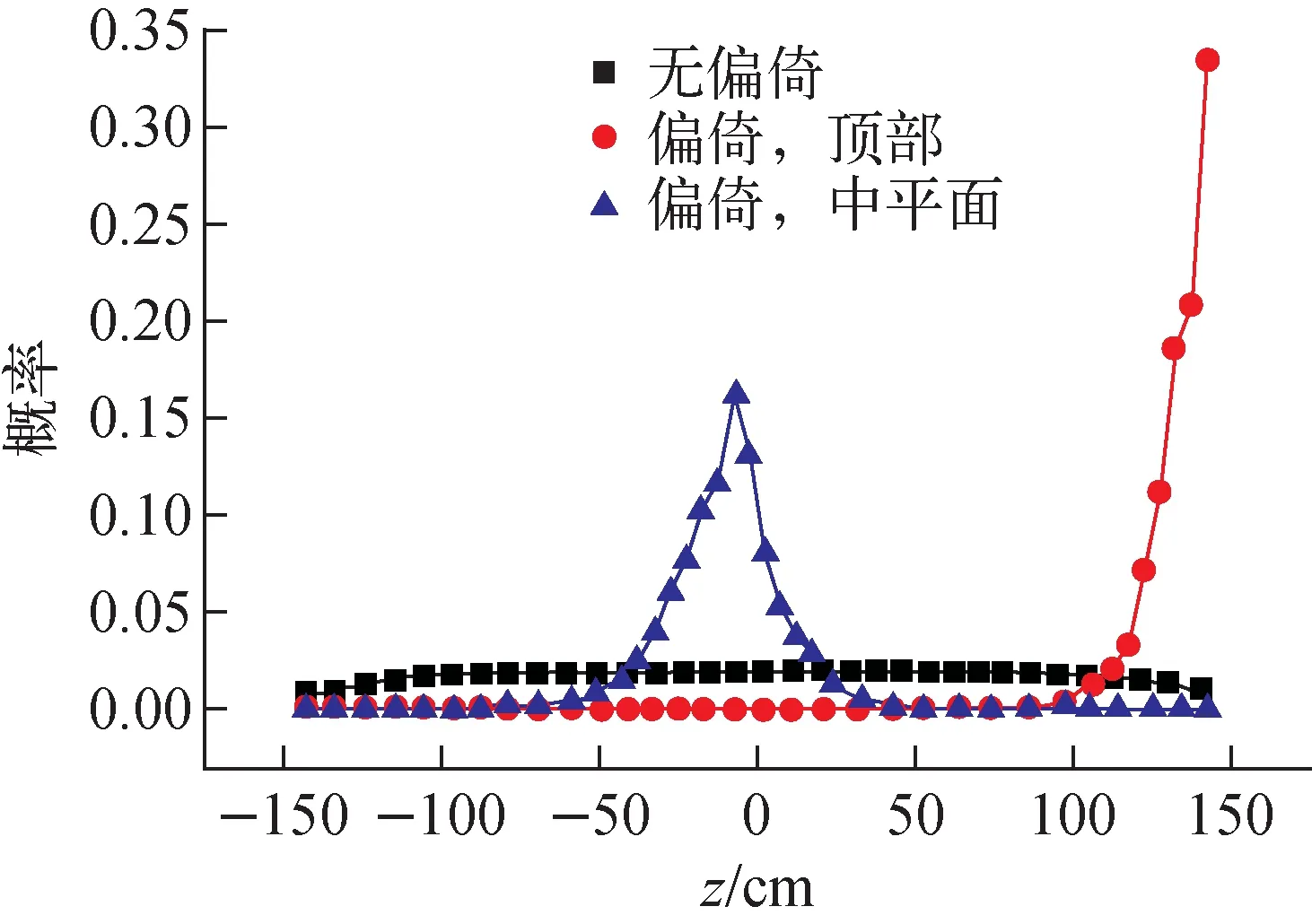

3 结论

