刚性限制法在瞬态中子输运计算中的应用
汤春桃,毕光文,杨 波
(上海核工程研究设计院有限公司,上海 200233)
中子动力学方程是描述核反应堆系统瞬态过程中堆芯动态特性的基本控制方程之一。目前工业级设计程序主要采用两群瞬态中子扩散模型求解点堆动力学或三维时空动力学方程,该方法的成功运用在核电厂低功率物理启动试验动态控制棒价值测量和反应堆事故分析中发挥了关键作用。随着新型反应堆堆芯(如小型堆、超临界水堆、铅基堆)和新型燃料组件(如MOX燃料)的研发与设计,现行两群瞬态中子扩散模型正面临越来越多的技术挑战。伴随数值反应堆技术的蓬勃发展与硬件计算能力的飞速提升,有必要开展瞬态多群中子输运方程求解方法的研究。
刚性限制法(SCM)利用动态频率变换技术,实现中子通量密度平衡方程与缓发中子先驱核密度平衡方程的解耦,将动力学方程中的刚性问题淹没在稳态方程的求解过程中[1-2],确保在较大时间离散步长情况下获得较高的计算精度,大幅提升了计算效率。SCM已在两群瞬态中子扩散方程求解中获得了广泛应用[3-5]。
本文将SCM拓展应用于求解多群瞬态特征线中子输运方程,在原有中子输运方程特征线方法(MOC)求解程序PEACH[6]的基础上,增添瞬态求解功能,开发PEACH-K程序,并通过数值模拟验证其精度与稳定性。
1 时空中子动力学模型
1.1 瞬态中子输运方程的动态频率变换
时间相关的多群中子输运方程和缓发中子先驱核密度方程为:
(1)
(2)
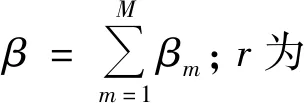
考虑到在反应堆物理中通常假设裂变中子各向同性,Cm主要来自于裂变,因此式(2)中Cm假设与方向无关。
引入以下中子通量动态频率ωg和缓发中子先驱核密度动态频率μm:
(3)
(4)
(5)
将式(3)和(5)代入式(1)、(2),再引入ωg(r,Ω,t)各向同性假设,用ωg(r,t)近似替代ωg(r,Ω,t),动力学方程变换为如下形式:
(6)
其中:Σ′t,g为动态总截面;χ′g为动态瞬发中子裂变能谱。
式(6)的中子通量仍是各向异性的。Σ′t,g和χ′g的计算表达式如下:
(7)
(8)
式(6)与稳态中子输运方程具有相同的形式。在动力学数值迭代过程中,一旦获得动态频率ωg和μm后,可采用稳态中子输运方程MOC对式(6)进行求解。需要说明的是,式(4)中的φg(r,t)为MOC最小平源近似区的标量中子通量。
1.2 动态频率的迭代更新
式(6)是一本征值问题。与求解稳态中子输运方程类似,可引入一动态本征值kD,这样式(6)可转换为:
(9)
其中,动态参数Σ′t,g和χ′g是动态频率的函数。迭代收敛时,kD等于1。利用式(4)和(9)可对ωg进行更新。然而式(9)求解的本征函数只是中子通量分布而非中子通量幅度。在缺乏中子通量幅度的情况下,动态频率则无法有效更新。为克服此问题,将动态频率分解为形状频率和幅度频率两部分:
ωg(r,t)=ωs,g(r,t)+ωt(t)
(10)
μm(r,t)=μs,m(r,t)+ωt(t)
(11)
其中,形状频率ωs,g、μs,m与位置、时间相关,而幅度频率ωt仅与时间相关,具备全局属性。
形状频率根据本征函数进行更新,幅度频率根据本征值进行更新。在迭代过程中,如果式(9)中的kD不等于1,那么可在动态频率的基础上增加一定的修正量Δωt,使得kD接近于1,此时要求以下关系成立:
(12)
令:
(13)
利用一阶泰勒展开,得到:
γg(ωt)+γ′g(ωt)·Δωt
(14)
其中,γ′g(ωt)=dγg(ωt)/dωt。将式(13)和(14)代入式(12)可得:
(15)
选取1组权重函数向量W,采用剩余权重法对式(15)进行能量和空间积分,可得:
(16)
其中:
(17)
l*=
(18)
至此,中子通量的动态频率可根据式(4)、(10)和(16)进行更新,缓发中子先驱核密度的动态频率可根据式(5)和(11)进行更新。针对权重函数向量W,在两群瞬态中子扩散方程求解时,建议选用共轭通量分布函数;在多群瞬态中子输运方程求解时,由于共轭通量分布函数需通过求解共轭方程才能获得,影响计算效率,建议选用裂变率分布函数。
1.3 缓发中子先驱核密度的求解
缓发中子先驱核密度采用解析法求解。在获得tn时刻的先驱核密度Cm(r,tn)后,将式(2)在tn~tn+1时间范围内积分,可得tn+1时刻的先驱核密度Cm(r,tn+1):
Cm(r,tn+1)=Cm(r,tn)·e-λmΔtn+e-λmΔtn·
(19)
其中,Δtn=tn+1-tn。
F(r,t)=F(r,tn)+
(20)
根据式(19)和(20)可解得:
(21)
这样,通过数值迭代求解获得新的中子通量密度后,即可根据式(21)有效地更新缓发中子先驱核密度。
1.4 数值迭代流程
在稳态中子输运方程MOC求解程序PEACH的基础上,根据上述动力学模型,开发了动力学求解程序PEACH-K,数值迭代流程如图1所示。
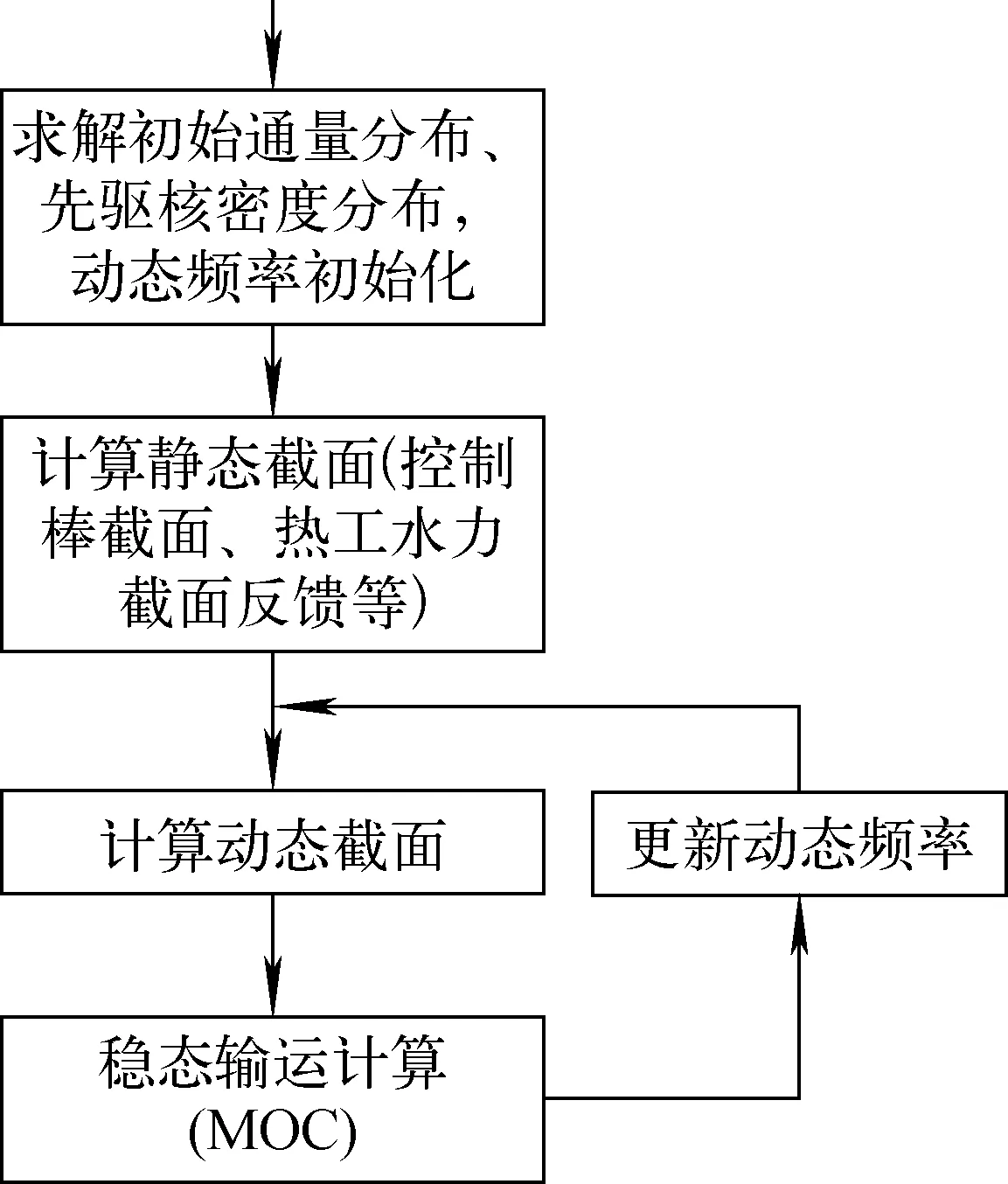
图1 PEACH-K程序动力学模型的数值迭代流程
2 数值验证
国际上现有瞬态基准问题多用于验证基于组件均匀化和少群扩散近似的动力学模型,鲜有针对瞬态中子输运方程的非均匀多群问题。为此,OECD/NEA于2016年发布了基准题C5G7-TD[7-8],含二维和三维,本文基于该基准题(二维)对PEACH-K程序进行数值验证。
2.1 C5G7-TD基准题描述
C5G7-TD基于OECD/NEA于2001年发布的基准题C5G7-MOX改造而来,用于瞬态非均匀输运模型验证。该问题堆芯由UO2燃料组件和MOX燃料组件混合装载,共计16盒燃料组件,呈1/8对称,具有强泄漏、组件间能谱差异大、非均匀性强等特点。图2示出该问题的1/4堆芯装载图,其中每个组件的几何尺寸为21.42 cm×21.42 cm,水反射层的宽度也为21.42 cm。该问题所使用的UO2和MOX组件均为17×17的元件排列方式,其中UO2组件内只有一种富集度的燃料元件棒,而每个MOX组件内则都有3种含量不同的MOX燃料栅元,详见文献[7-8]。

图2 二维C5G7-TD基准题堆芯布置
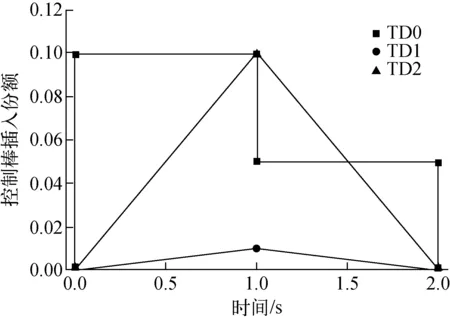
图3 TD0~2下控制棒的移动
C5G7-TD基准题基于不同的反应性引入方式,共设计了4种算例,针对每种算例又设计了多项分支工况。其中,前3种算例(TD0~2)采用控制棒引入反应性,第4种算例(TD3)采用慢化剂密度变化引入反应性。针对控制棒引入反应性的方式,图3示出了TD0~2下控制棒插入份额随时间的变化曲线。算例TD0和TD1分别设计了5项分支工况,算例TD2设计了3项分支工况,对应不同的控制棒组定义(表1)。针对慢化剂密度变化引入反应性的方式,图4示出了TD3各分支工况堆芯平均慢化剂密度随时间的变化曲线,图4中ω表示慢化剂密度随时间变化与初始工况(零时刻)的比例关系。
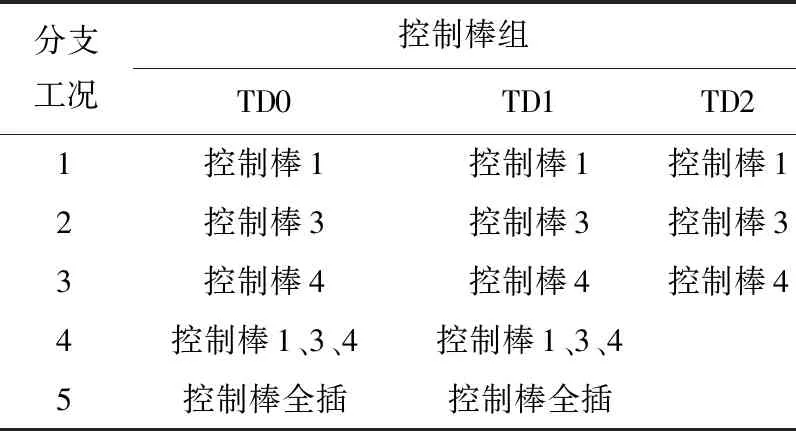
表1 TD0~2分支计算中控制棒组移动定义
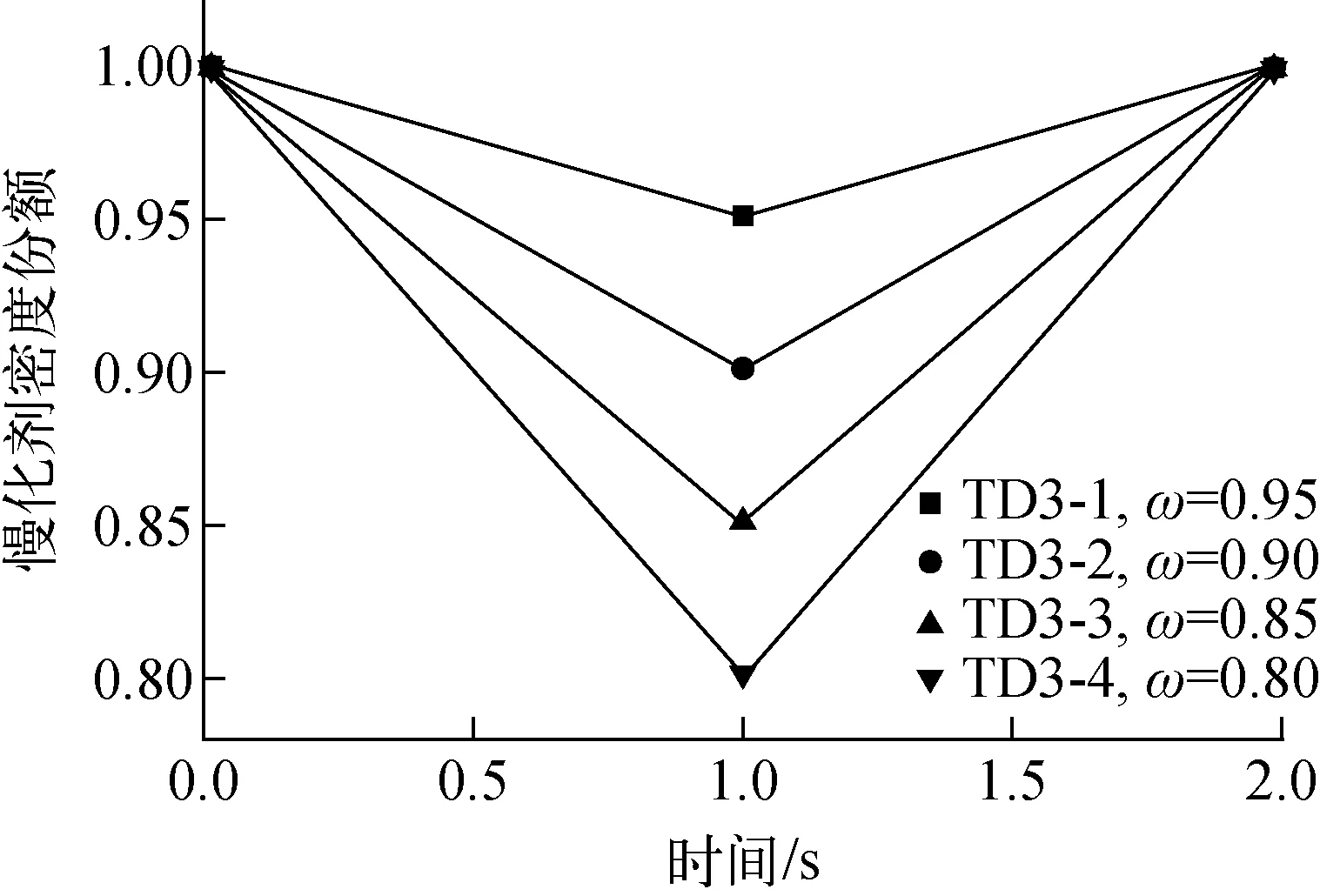
图4 TD3堆芯平均慢化剂密度的变化
2.2 基准题数值结果
C5G7-TD基准题的参考解目前还在搜集和整理阶段,本文采用NECP-X程序[9]作为比较基准,该程序采用预测-修正准静态的动力学求解方法。针对本基准题在前2 s反应性变化较剧烈的特点,NECP-X程序0~2 s采用的时间步长为0.025 s,2~2.5 s采用的时间步长为0.05 s,2.5~3 s采用的时间步长为0.1 s,3~10 s采用的时间步长为0.5 s,而PEACH-K程序在全时间区域内时间步长均采用0.25 s。图5~8示出各算例堆芯归一化功率水平的变化。总体来看,PEACH-K与NECP-X程序结果符合非常好,TD1~3的堆芯归一化功率水平的相对偏差均在1%以内,表明PEACH-K程序在大时间步长下仍具有很高的计算精度。
针对TD0,控制棒采用阶跃反应性引入方式,在个别拐点处(如TD0-1、TD0-4和TD0-5在2 s附近)由于控制棒价值太大引起了剧烈的功率突变幅度,PEACH-K与NECP-X程序的堆芯归一化功率水平的最大相对偏差在2%以内。在工程实际中,控制棒大幅度阶跃提升是不太可能出现的。
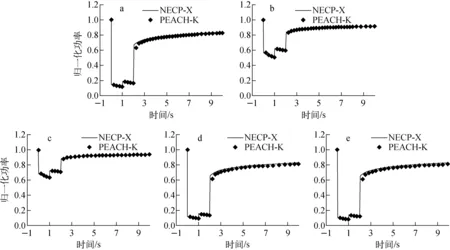
a——TD0-1;b——TD0-2;c——TD0-3;d——TD0-4;e——TD0-5图5 TD0堆芯归一化功率水平的变化

a——TD1-1;b——TD1-2;c——TD1-3;d——TD1-4;e——TD1-5图6 TD1堆芯归一化功率水平的变化
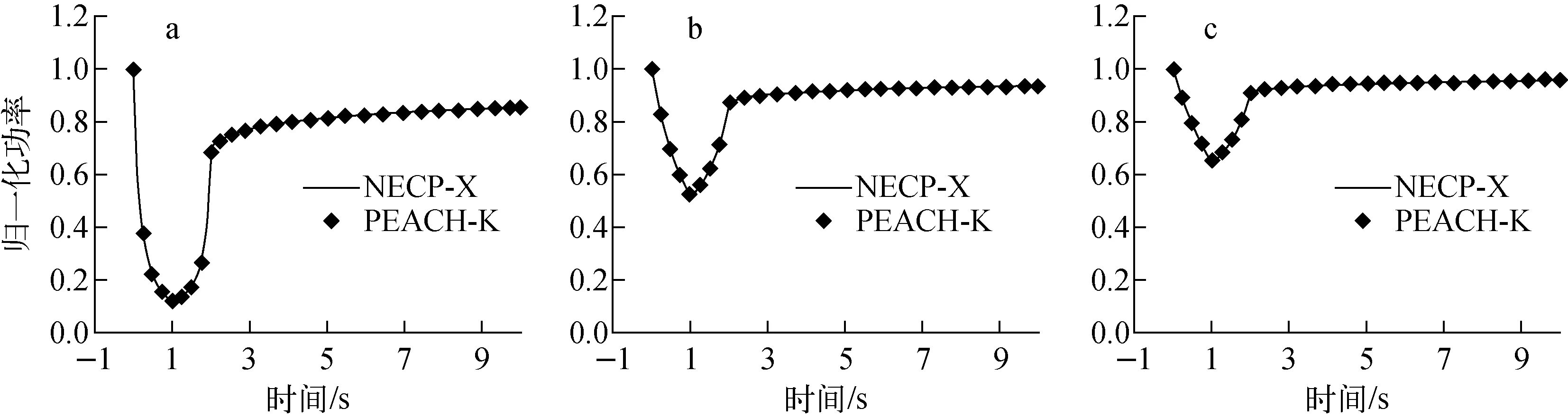
a——TD2-1;b——TD2-2;c——TD2-3图7 TD2堆芯归一化功率水平的变化
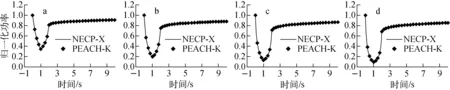
a——TD3-1;b——TD3-2;c——TD3-3;d——TD3-4图8 TD3堆芯归一化功率水平的变化
3 结论
本文介绍了刚性限制法在瞬态中子输运计算中的应用。采用OECD/NEA发布的C5G7-TD基准题对采用刚性限制法的PEACH-K程序进行了数值验证,结果表明PEACH-K程序在大时间步长下仍具有很高的计算精度,刚性限制法可用于非均匀输运瞬态计算。
感谢美国西屋公司退休专家赵荣安博士在刚性限制法研究方面的鼓励。感谢西安交通大学刘宙宇博士提供C5G7-TD基准题NECP-X程序的对比结果。

