NECP-X中基于改进泄漏项分割技术的二维/一维耦合输运方法

赵 晨，刘宙宇，曹良志，吴宏春

(西安交通大学 核科学与技术学院，陕西 西安 710049)

当前计算机发展水平下，二维/一维耦合输运因兼顾计算精度和计算效率已被广泛应用于全堆芯一步法输运计算[1]。二维/一维耦合输运方法将一个三维问题分为一系列径向二维问题和轴向一维问题，并通过泄漏项进行耦合。国际上，对于二维/一维耦合方法进行了较为广泛的研究，基于该方法开发了一系列程序，包括CRX-3D[2]、DeCART[3]、nTRACER[4]、MPACT[5-6]等。

国内外对于二维/一维耦合输运方法的研究主要集中在精度、稳定性、效率、内存几方面。一维输运方法研究[7]和泄漏项重构方法[8]提高了二维/一维耦合输运方法的计算精度；通过基于空间、角度、特征线的多重并行很好地解决了内存及效率问题[9]。由泄漏项造成的稳定性问题，成为二维/一维耦合输运方法中最重要的问题之一。对于径向二维特征线法(MOC)方程，方程右端的轴向泄漏项造成总源项可能出现负值，由此可能造成计算过程中产生负通量导致迭代发散。对于轴向采用扩散方法、泄漏项采用各向同性近似的二维/一维耦合方法，密歇根大学通过引入松弛因子提高了稳定性[5-6]，但该方法对于各向异性泄漏项并不完全适用，且松弛因子方法并未从本质上解决负源项造成的收敛性问题。针对基于各向同性泄漏的二维/一维耦合方法的不稳定问题，MPACT通过泄漏项分割方法，提高了稳定性的同时保持了较好的精度。但对于各向异性泄漏项的二维/一维耦合方法，该方法会带来十分严重的精度损失。针对各项异性泄漏项的二维/一维耦合输运方法，国际、国内均未做相关研究。

本文基于西安交通大学开发的数值反应堆物理计算软件NECP-X[10-14]，对原有的基于标通量的泄漏项分割方法进行分析，针对各向异性泄漏项的二维/一维耦合方法提出改进的泄漏项分割方法，在内存稍有增加的情况下，解决二维/一维耦合方法中存在的稳定性问题，同时克服原有泄漏项分割方法精度损失的问题。

1 理论模型

1.1 二维/一维耦合输运方法及负源项问题

角度能量离散后的三维中子输运方程可写为如下形式：

Qg(x,y,z)

(1)

其中：ε、η、μ分别为x、y、z方向的方向余弦；Σt,g(r)为总截面；ψg,m(x,y,z)为空间(x,y,z)上m方向的角通量，即中子输运方程中的未知量；Qg(x,y,z)为总源项，包括裂变源及散射源，具体形式如下：

(2)

其中：χg为裂变谱；(νΣf)g′为第g′群的裂变截面；Σs0,g′→g为第g′群到第g群的散射截面；φg′(x,y,z)为标通量。

将式(1)在轴向层L内进行积分，得到径向二维方程：

(3)

(4)

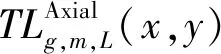
将式(1)在径向棒p内进行积分，得到轴向一维方程：

(5)

(6)

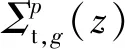
NECP-X程序轴向计算采用SN差分方法，基于不作近似的各向异性泄漏项进行耦合，二维/一维迭代直至特征值和裂变率收敛。迭代过程中，由于轴向泄漏项的存在造成式(3)右端源项可能出现负值，在MOC计算过程中，负源项有可能造成沿特征线的出射角通量、平均角通量为负，从而在二维计算中产生负通量，导致迭代发散。

1.2 泄漏项分割方法

泄漏项分割方法的基本公式如下：

Σt,g(x,y)ψg,m(x,y)+ΣL,g(x,y)ψg,m(x,y)=

(7)

其中，

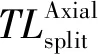
各向同性泄漏项和基于标通量的泄漏项分割方法被应用于MPACT程序中，并取得了较好的效果。但对于各向异性泄漏项，基于标通量的泄漏项分割方法会造成不可接受的精度损失，因此需要一种适用于各向异性泄漏项的改进的泄漏项分割方法。

1.3 改进的泄漏项分割方法

式(7)中最精确的选择是选择各平源区各角度的角通量进行泄漏项分割，如式(8)～(10)所示。这样处理后的式(7)与式(3)完全等效，未作任何近似。然而这种方法需存储每个平源区每个角度每个能群的角通量，对于大规模问题这种方法带来的内存负担是无法接受的，因此不具备实际应用价值。

(8)

Qg(x,y),0)

(9)

(10)

对此，本文提出了改进的泄漏项分割方法消除二维/一维耦合方法中的负源项问题，并在内存可接受的情况下保持二维/一维耦合计算的精度。因此应基于角通量的泄漏项分割技术，并且不保存平源区的角通量从而降低内存需求。

为数值上显示棒内平均角通量和平源区角通量的分布特点，设计了1个强泄漏算例，如图1所示。燃料棒在径向为3×3布置，沿轴向布置2层燃料和1层水，分析的3个平源区分布也如图1所示。计算条件为：1个卦限内采用8个幅角3个极角，第1群的棒内平均角通量分布如图2所示，第1群的3个平源区内角通量分布如图3所示。

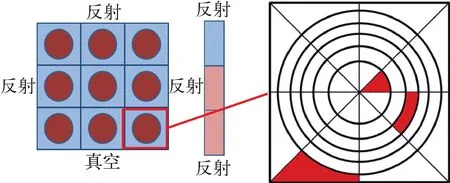
图1 强泄漏算例几何及棒内平源区分布

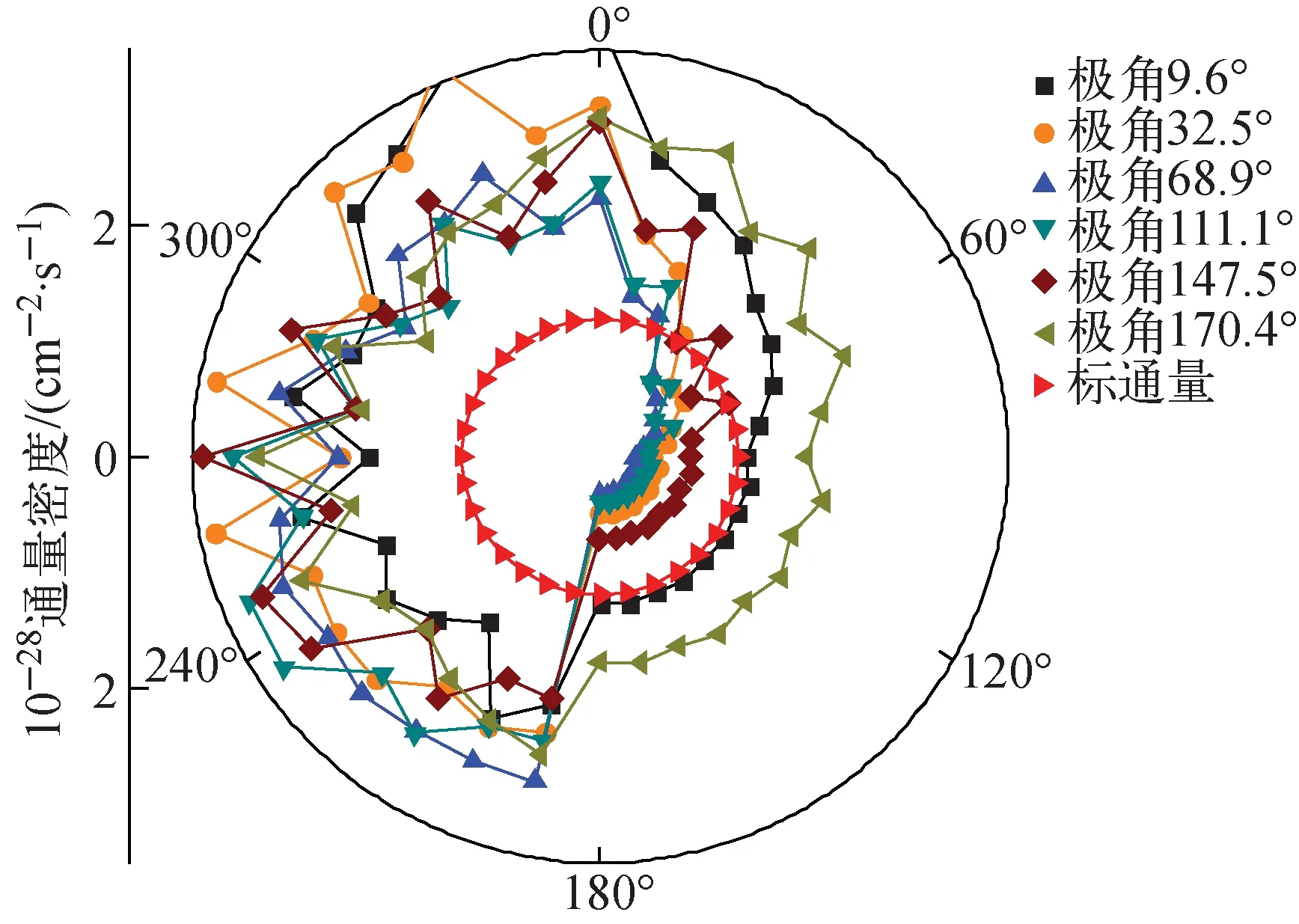
图2 第1群棒内平均角通量分布

如图2、3所示，每条线表示特定极角方向上角通量沿幅角的分布，棒内均匀化的角通量分布与3个平源区的形状类似，因此棒内均匀化的角通量分布可近似表示棒内各平源区的各向异性效应。基于以上近似，各平源区内的角通量分布可采用标通量和棒内均匀化的角通量分布重构得到，即：

(11)

其中：m为角度序号；i为平源区序号；pin代表棒内均匀化通量。

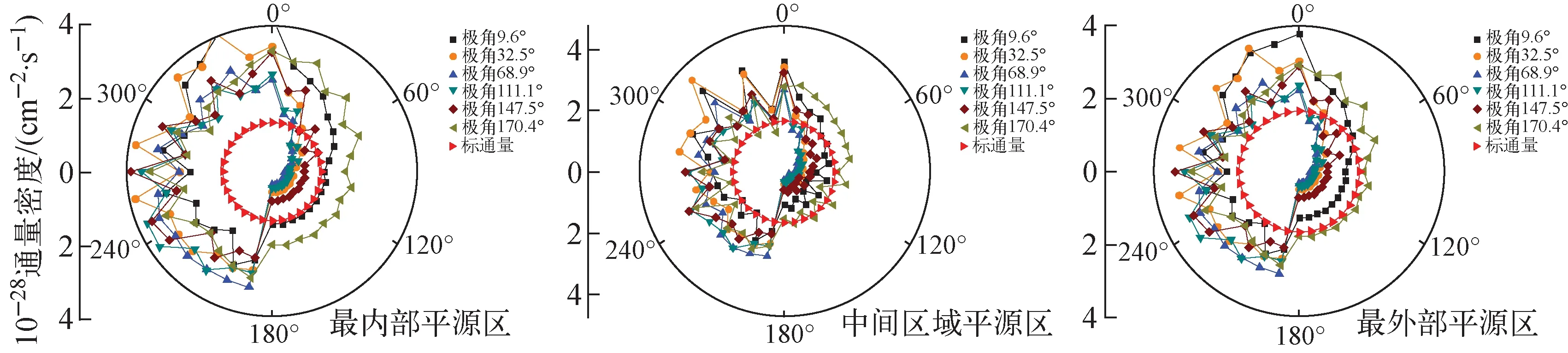
图3 第1群各平源区角通量分布

基于这种重构方法，仅需存储棒内均匀化的角通量，存储量与泄漏项相同，在可接受范围内。与原有泄漏项分割方法相比，在较小内存需求下获得平源区的角通量分布，实现基于角度各向异性的泄漏项分割技术，提高二维/一维耦合方法计算精度。

2 数值结果

2.1 计算精度分析

1) 强泄漏算例

该算例中，强泄漏和强各向异性效应通过设置径向真空边界条件引入，几何如图1所示。燃料棒在径向3×3布置，沿轴向布置2层燃料和1层水。基于这个3×3算例，可将问题拓展至7×7、17×17等更大规模，建立不同的各向异性问题，从而研究各向异性对计算精度的影响。

该算例中，二维/一维耦合方法未出现负源项引起的迭代发散问题，因此可采用不带泄漏项分割方法的二维/一维耦合方法的结果作为基准解，比较传统基于标通量的泄漏项分割方法、改进的泄漏项分割方法、基于平源区角通量的泄漏项分割方法的计算结果。特征值计算结果列于表1。传统基于标通量的泄漏项分割方法严重影响计算精度，泄漏越强各向异性越强，计算精度越差。采用改进的泄漏项分割方法可显著地提高计算精度，最精确的是基于平源区角通量的泄漏项分割方法。

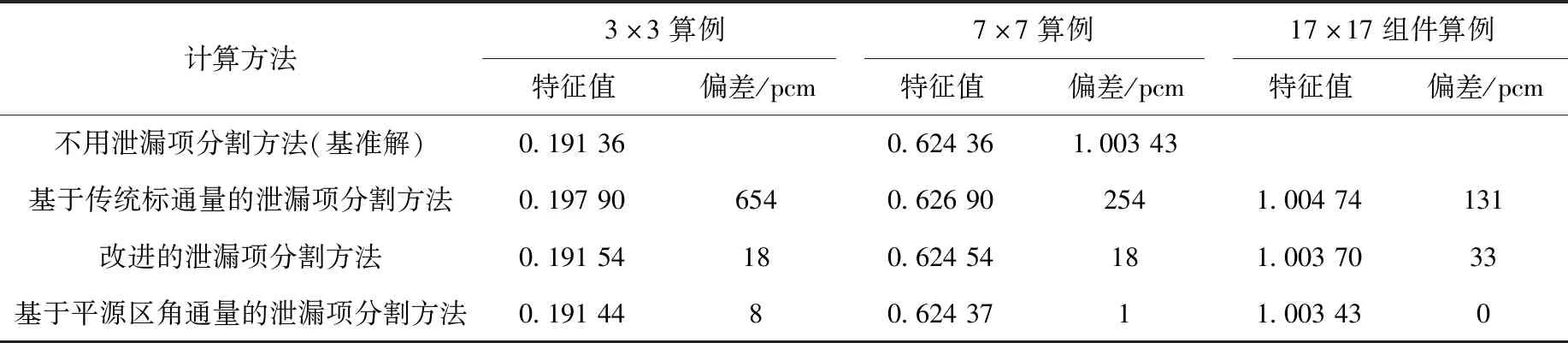
表1 强泄漏算例的特征值计算结果

2) C5G7基准题全插棒算例

C5G7 OECD/NEA是知名输运计算基准题，包括不带棒(unrodded)、半插棒(rodA)、全插棒(rodB)3个算例，表2列出了全插棒算例的计算结果。计算过程中，燃料棒采用48个平源区、反射层棒采用64个平源区，1个卦限内采用8个幅角3个极角，特征线宽度为0.03 cm。轴向上，燃料区分12层，反射层区分6层，每层3.57 cm。轴向细网为1 cm。

从表2可看出，改进的泄漏项分割方法特征值与基准解相比相差45 pcm，全局最大棒功率偏差为1.94%，计算精度较好，与不用泄漏项分割方法的计算精度相当。然而基于传统标通量的泄漏项分割方法，特征值偏差达到300 pcm，最大棒功率偏差为15%。结果表明，传统泄漏项分割方法对于C5G7这类具有较强各向异性的算例会带来较为严重的精度损失，而改进的泄漏项分割方法可获得较高的计算精度。

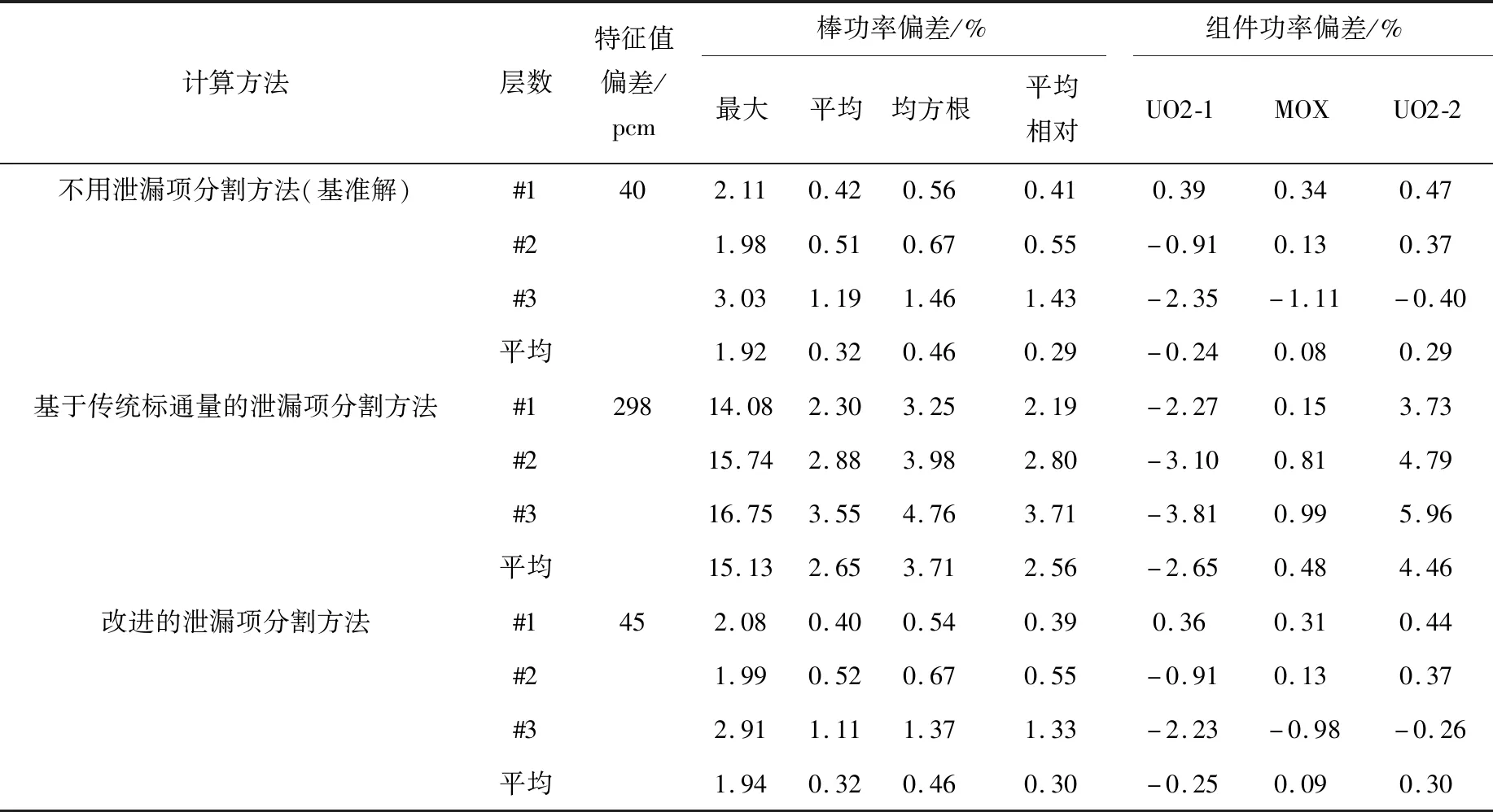
表2 C5G7 rodB算例计算结果

3) VERA-3A基准题算例

VERA基准题发布于2014年，提供了从栅元到堆芯、从二维到三维的一系列基准题，数据多来自Batts Bar压水堆核电站，因此该基准题是具有真实参数的实际问题。VERA-3A是一个三维组件问题，在NECP-X程序中，对复杂几何进行了详尽描述，包括格架、上下管座、下端塞等。燃料棒划分40个平源区、反射层划分64个平源区，1个卦限包括8个幅角3个极角，特征线线宽为0.03 cm，轴向划分66层，采用66个核并行。表3列出了特征值和棒功率计算结果，图4～6示出了轴向、径向棒功率分布结果。与KENO计算结果相比，特征值偏差小于20 pcm，最大棒功率偏差约1%，表明改进的泄漏项分割方法具有较高的计算精度。

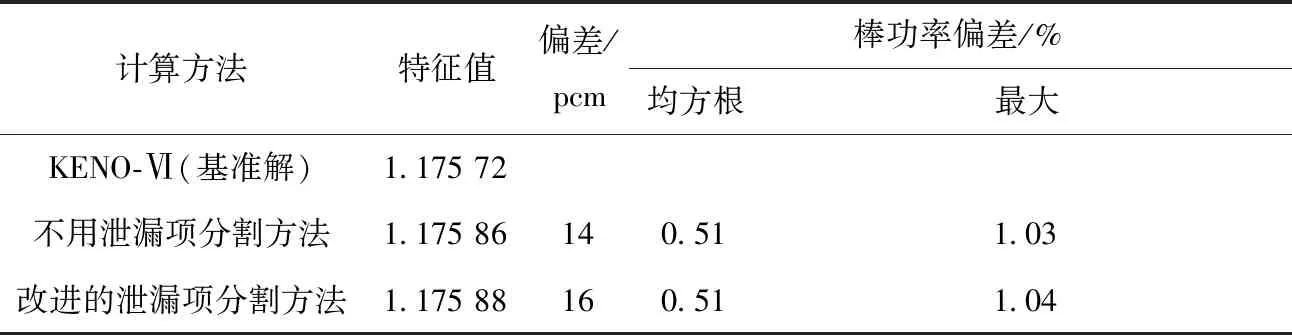
表3 VERA-3A基准题计算结果

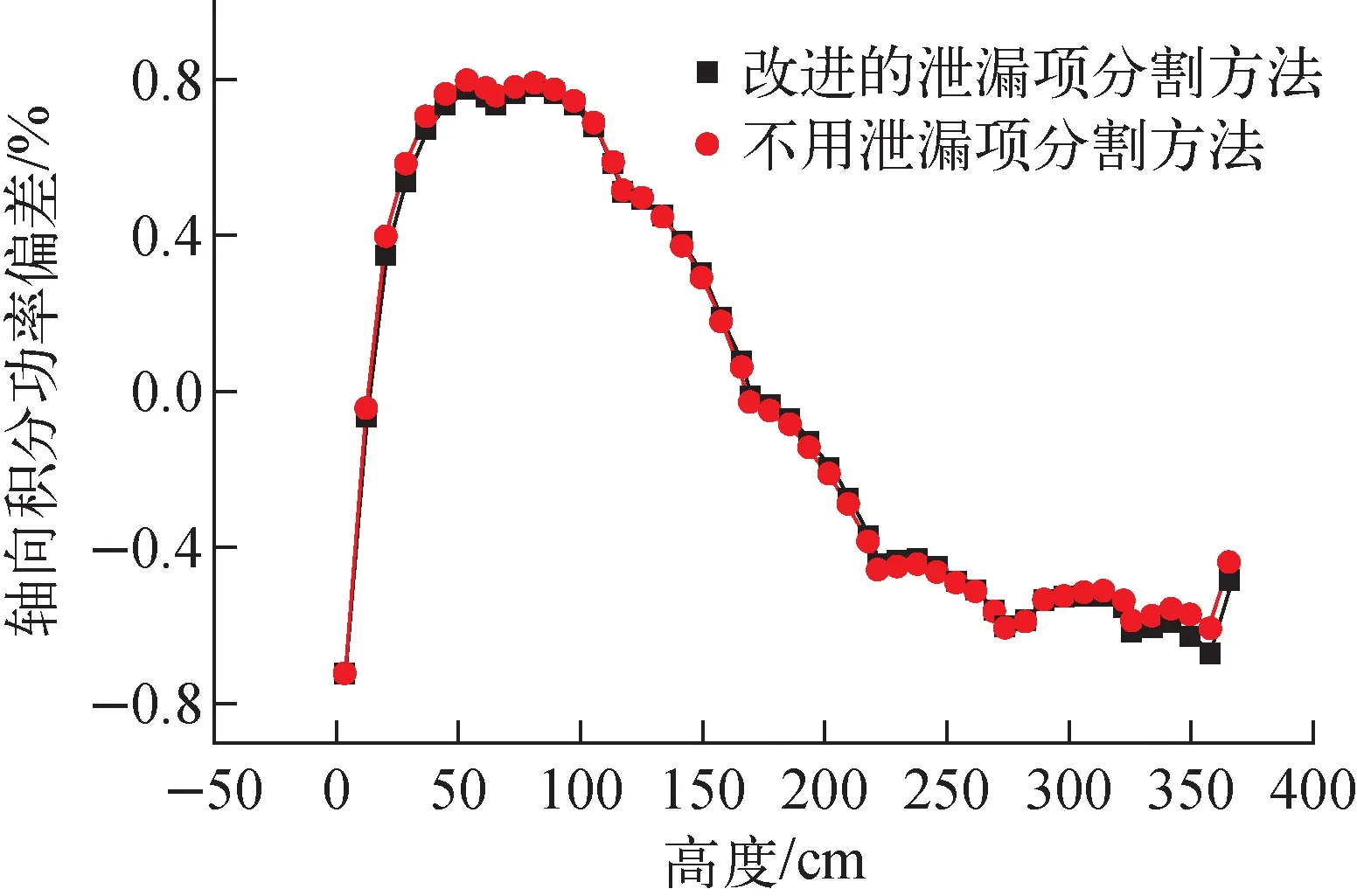
图4 VERA-3A基准题轴向积分功率偏差

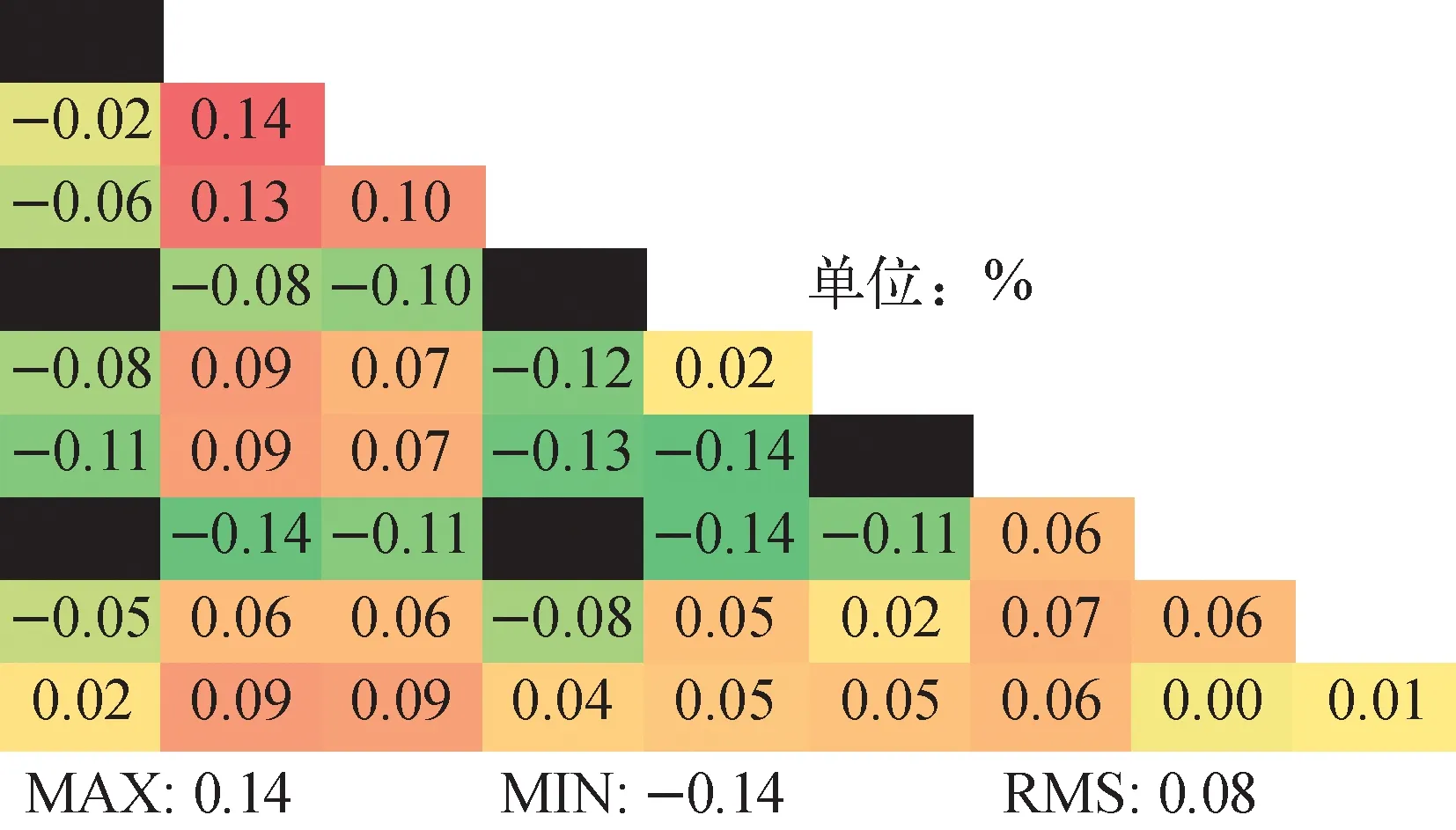
图5 VERA-3A基准题不用泄漏项分割方法径向积分功率偏差

图6 VERA-3A基准题改进的泄漏项分割方法径向积分功率偏差

2.2 内存分析

本文针对2个7群算例分析了改进的泄漏项分割方法的内存要求，1个是7群轴向6层单组件算例，另1个是C5G7基准题全插棒算例。计算条件与C5G7基准题完全一致，内存使用量列于表4。计算结果表明基于平源区角通量的泄漏项分割方法占用的内存是不用泄漏项分割方法的8倍，对于C5G7基准题，该方法已无法在64G单节点上进行计算，因此对于更大规模问题，这种基于平源区角通量的泄漏项分割方法是不实用的。另一方面，改进的泄漏项分割方法虽然内存占用有所增加，但增加量较小，对于C5G7基准题仅增加9.5%，该方法在更大规模问题上仍是可接受的。

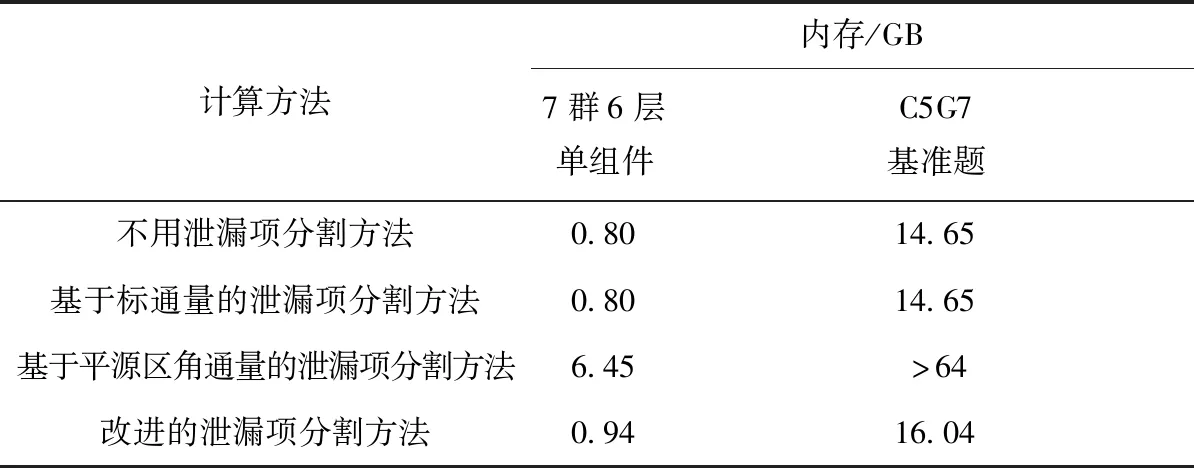
表4 基于7群算例的内存分析结果

2.3 稳定性分析

在1.1节介绍了二维/一维方法中潜在的负源项造成迭代发散的问题。对于VERA-3A基准题算例，计算条件与VERA-3A基准题完全相同，使用outflow输运修正，分别利用24个核和66个核进行并行计算。因为在迭代过程中，反射层区域出现了很负的源项，导致了迭代发散的问题。而改进的泄漏项分割方法可解决负源项造成的迭代发散问题，计算结果列于表5。

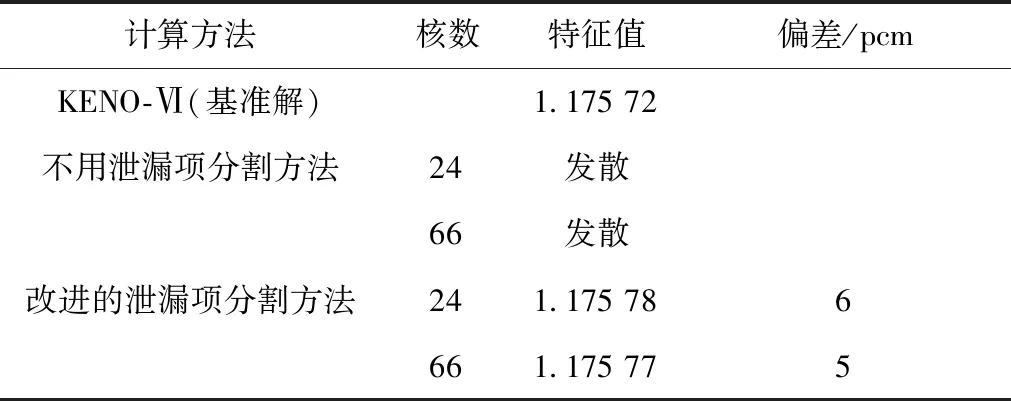
表5 对于VERA-3A基准题的稳定性分析结果

3 总结

二维/一维耦合输运方法中由于泄漏项的存在，导致潜在不稳定的问题。针对各向异性泄漏项，传统的基于标通量的泄漏项分割方法在计算强各向异性问题时，会造成较大的精度损失。本文提出了一种改进的泄漏项分割方法，在不造成精度损失的情况下解决了二维/一维耦合输运方法中的稳定性问题。

改进的泄漏项分割方法中，通过棒内均匀化角通量分布和平源区标通量在线重构平源区角通量分布。数值结果表明棒内均匀化的角通量分布可近似模拟平源区的角度各向异性，从而在不保存平源区角通量的情况下保持二维/一维耦合输运方法的计算精度。

通过强泄漏算例、C5G7基准题、VERA-3A基准题分析了改进的泄漏项分割方法的计算精度、内存要求和稳定性。数值结果表明，改进的泄漏项分割方法可在增加有限内存的条件下，保持二维/一维耦合方法的计算精度，并显著提高其稳定性。