自适应局部稀疏线性嵌入降维算法

吴 青, 祁宗仙, 臧博研, 张 昱

(西安邮电大学 自动化学院， 陕西 西安 710121)

流形学习[1]是利用流形局部欧氏空间进行维数约简的算法，可有效降低高维非线性数据的维度。常见的流形学习包括局部线性嵌入(locally linear embedding, LLE)[2]，拉普拉斯特征映射(laplacian eigenmaps, LE)[3]，距映射算法(isometric mapping, ISOMAP)[4]和局部切空间排列(local tangent space alignment, LTSA)[5]等。LE采用局部领域相似度表示流形的距离，计算复杂度低但精度不高。ISOMAP采用测地线距离表示全局流形上的距离，降维的精度高但复杂度也高，不适合大量数据降维。而LLE是假设数据在很小的局部空间邻域上，可近似看成线性相关，每个数据点都可由它最近的几个点线性表示，具有算法思想直观、易实现和速度快等优点，已广泛应用在深度学习和故障检测等方面。

融合聚类的监督局部线性嵌入算法[6]计算近邻点距离时，利用类别标签加入类别信息的权，使得样本近邻点多数为同类样本，少数为异类样本，重构时可尽量保持数据的分布信息，但需要样本提供类别信息，适用性较小。领域选择的LLE算法[7]运用系数主分量估测每个样本点噪声的概率，避免了选择高概率噪声的样本点作为近邻点。在数据集稀疏的情况下，稀疏局部线性嵌入算法[8]利用数据的统计信息动态确定局部线性化范围，能够较好地把握数据的局部和整体信息，提高了算法的抗噪性，但没有解决权重矩阵奇异性的问题。局部稀疏线性嵌入(locally and sparsely linear embedding, LSLE)算法[9]采用正交匹配追踪算法求解权重矩阵，避免了求权重矩阵的逆运算,但在实时的动态系统中，有效近邻点的个数未知，依然存在近邻点选择不恰当的问题。

为了优化近邻点选取和避免权重矩阵奇异，本文提出一种自适应局部稀疏线性嵌入方法(locally and sparsity adaptive linear embedding, LSALE)。采用压缩感知(compressed sensing, CS)[10-12]中的稀疏度自适应匹配追踪算法(sparsity adaptive matching pursuit, SAMP)[13-15]求解样本点的近邻权重系数，自适应地选择有效近邻点，避免权重矩阵求逆。依据数据分布不同，自动为每个样本点进行二次选择近邻点，避免将噪声选为近邻点。

1 局部线性嵌入

在局部空间内，数据样本点xi(i=1,2,…,n)可由离它最近的k个样本点x1,x2,…,xk线性[1]表示为

xi=wi1x1+wi2x2+…+wikxk。

(1)

其中wi1,wi2,…,wik为权重系数。利用LLE降维后，xi的低维映射像x′i，则可由x1,x2,…,xk对应的像x′1,x′2,…,x′k线性[1]表示为

x′i=wi1x′1,wi2x′2,…,wikx′k。

(2)

映射前后线性关系的权重系数wi1,wi2,…,wik不变。

显然，xi只需要求得k个近邻点x1,x2,…,xk的权重系数便可以降维，无需全局参与运算，即可降低计算量，提高运算效率。因此，LLE算法要先求解原空间中每个样本点线性表示的权重系数，然后利用样本点在原空间的权重系数，求它在某低维空间的像。

1.1 权重系数

已知数据集{x1,x2,…,xn},xi∈D，确定样本点xi的k个最近邻点，求出xi和k个最近邻点之间的线性关系，即找到线性关系的权重系数，满足[2]

(3)

其中，xj为xi的近邻点，wij为xj的权重系数。

利用最小二乘方法求得xi所有近邻点的权重向量[2]为

(4)

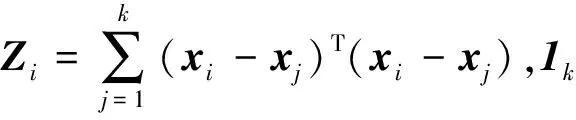
(5)

式中，α为极小的常数值，I为k×k阶单位矩阵，tr(Zi)表示Zi的迹。

无参数和非迭代的特性使得LLE计算量小，容易实现，但求解权重矩阵时需要求Zi的逆，若Zi奇异，则式(4)解不存在；添加扰动项式(5)，则可求得式(4)解，但影响了降维效果。同时LLE选取近邻点采用欧氏距离准则，在高维空间中容易把不在同一个线性空间的点选为近邻点，影响数据降维的有效性。LLE近邻点选取示意图如图1所示。

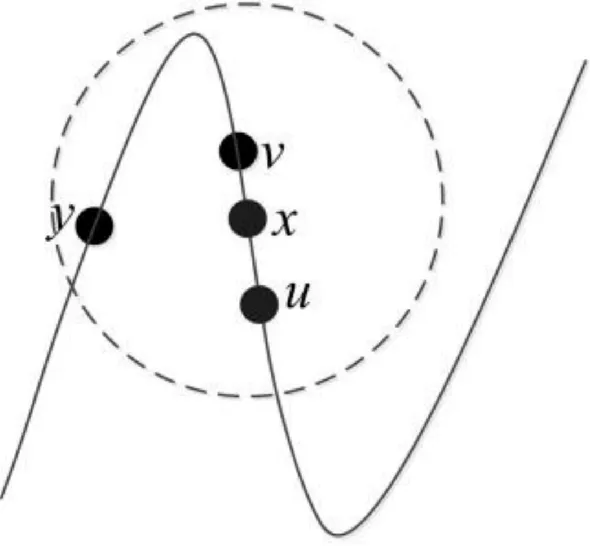
图1 LLE近邻点选取

1.2 低维映射

利用权重向量wi对数据降维。假设D维样本集{x1,x2,…,xn},xi∈D在低维空间d对应的投影为{y1,y2,…,yn},yi∈d,保持相同的线性关系，则低维映射满足[2]

(6)

其中yi为xi降维后的样本点，yj为yi的近邻点。I是单位矩阵。

将式(6)中的目标函数矩阵化[2]为

J(y)=tr[YT(I-W)T(I-W)Y],

(7)

其中

Y=(y1,y2,…,yn),
W=(w1,w2,…,wn)T。

令M=(I-W)T(I-W)，则式(7)可以表示为

J(y)=tr(YTMY)。

(8)

通过拉格朗日乘子法，对Y求导并令其为0，得到MYT=λYT。式(8)的解等价于求M的特征值对应的特征向量。为使式(6)取最小值，选择M中最小的d个特征值对应的特征向量。由于最小的特征值无限接近于0，所以应取第二个到第d+1个特征值对应的特征向量组成低维映射Y。

2 局部稀疏自适应线性嵌入

在LSALE中，采用SAMP算法求近邻点的权重矩阵，其每次迭代都能从近邻点矩阵找到与当前样本点残差最接近的近邻点，依次选取近邻点重构样本点，即最接近x的v和u优先被选取，当残差为0时，则x被重构，最远的y不会被选取。LSALE近邻点选取示意图如图2所示。

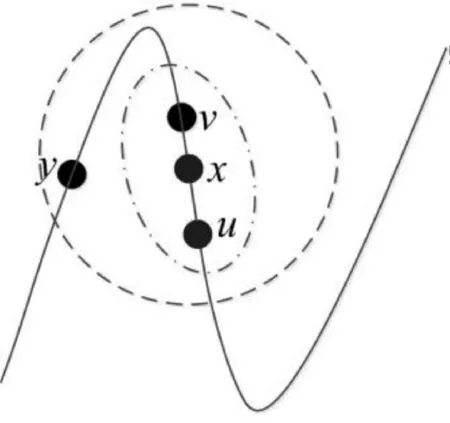
图2 LSALE近邻点选取

2.1 稀疏度自适应匹配追踪

采用SAMP算法求解LLE的权重矩阵，利用样本点被重构的残差动态地选取有效近邻点。SAMP的优化问题[13-15]为

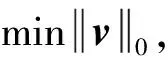
(9)

其中v是稀疏向量，u是观测向量，A是稀疏矩阵，‖·‖0表示求解0范数。SAMP算法以观测向量u和残差r为参考，从矩阵A中选出与当前样本点残差最接近的列向量，重构稀疏向量v，得到重构向量v′，并根据残差判断v′的重构情况。

在SAMP算法中，将观测矩阵A中选出与当前残差ra-1最相近的e个列向量的下标存放在预选集Sa中，a为迭代次数，则对应在观测矩阵A的列向量集合为ASa。支撑集Fa存放用于重构v的列向量下标，首次迭代为空集。通过残差ra-1选择A中列向量集合AFa重构v，并将其下标放在支撑集Fa中。合并预选集Sa与支撑集Fa-1得到候选集Ca，对应的列向量集合为ACa。将ACa中元素与u內积，找到与v最接近的e个列向量的下标，放入支撑集Fa中。

通过Fa更新残差

(10)

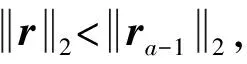
由此可见，SAMP算法通过候选集Ca回溯的方法，将新加入的列向量与选好的列向量进行择优选取，实现全局最优选取。

2.2 局部稀疏自适应嵌入

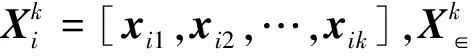
(11)

式(10)中0范数正则化[16]的引入，可稀疏wi，再通过式(8)，求解得出低维映射Y。

LSALE算法具体步骤如下。

输入高维样本矩阵

X=[x1,x2,…,xn]∈D，

近邻点个数为k，低维空间维数为d，其中D>d。

输出低维样本矩阵

Y=[y1,y2,…,yn]∈d。

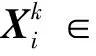
步骤2利用式(11)计算每个样本点xi的k个近邻点的权重向量wi。

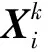
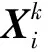
max{|x|,e}作用在于返回一个下标集，且该下标集由向量x的前e个最大值所对应的下标构成，“*”表示共轭转置。将预选集Sa与支撑集Fa-1合并为候选集，即

Ca=Fa-1∪Sa。

支撑集

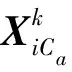
步骤5根据式(10)，得出残差

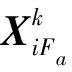
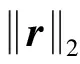
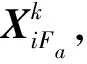
步骤8将所有的重构权重向量w′i组成权重矩阵W，利用式(8)求得低维映射Y，降维结束。

3 实验结果分析

选取UCI数据集中的Wine数据和MNIST手写体数据[17-18]，分别利用LSALE与LLE、LSLE和自适应邻域选择的局部线性嵌入(improved locally linear embedding, ILLE)[19]降维算法对数据进行降维，根据Libsvm工具箱[20]对降维数据进行分类，对比分类正确率。Libsvm中的核函数选择径向基核函数。实验环境为Intel(R)Core i7-6700HQ CPU、8G内存和MATLAB R2015A。

3.1 Wine数据集

Wine数据集是一组13维的3类数据。Wine数据集分别进行近邻点选择k对数据正确率的影响和不同低维维度d对数据正确率的影响两组实验。

实验1近邻点选择k对数据正确率的影响。通过寻找Wine数据集最适合的近邻点个数，对比LLE和LSALE算法k值不同对分类结果的影响。降维维度d=4，e=2。LSALE和LLE算法k值变化对分类正确率的影响如图3所示。

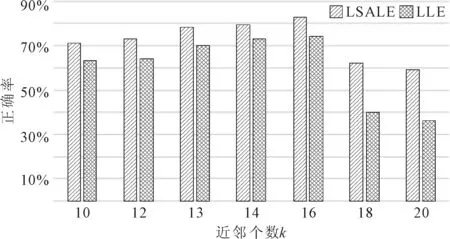
图3 LSALE和LLE不同近邻点的分类正确率

从图3中看出，当k值小于18时，两个降维方法的降维效果都不错；但当k值超过18时，LLE降维效果明显下降。邻域选择过大时，将大量错误点选为近邻点，导致邻域不具备为局部线性的性质，低维映射的数据结构信息被破坏，从而失去了降维的意义。LSALE由于其自适应的能力，对于邻域进行二次选择，尽管k值超过18，依然保持较好的降维分类效果。

实验2不同低维维度d对数据正确率的影响。取实验1中分类正确率最高的近邻点个数k=16，稀疏度S=2。利用Libsvm，分别对未降维时的原始数据、LLE降维、LSLE降维和LSALE降维后的数据进行分类，结果如图4所示。

图4 Wine数据集分类结果对比

图4结果表明，LSALE降维后的数据分类正确性优于LLE和LSLE。与原始数据相比，LSALE大幅度降维即当d<6时，原样本特征缺失，分类效果不理想，但d≥8时，LSALE的分类效果要明显优于原始数据的分类结果。

3.2 MNIST数据集

MNIST数据包含数字为0～9的手写体图片。对MNIST中数字为1、3、7等3类相似的数据进行降维分类实验。将全部18 319个数据进行降维，然后分别选取3类数据的20%，共3 664个数据进行测试。当k=10，d=20时，对不同稀疏度S进行降维处理，稀疏度S为二次选择的近邻点个数。利用Libsvm，分别对未降维的原始数据、ILLE[17]降维、LSLE降维以及LSALE降维后数据进行分类，取10次分类结果的平均值。MNIST数据的分类正确率和运行时间如表1所示。

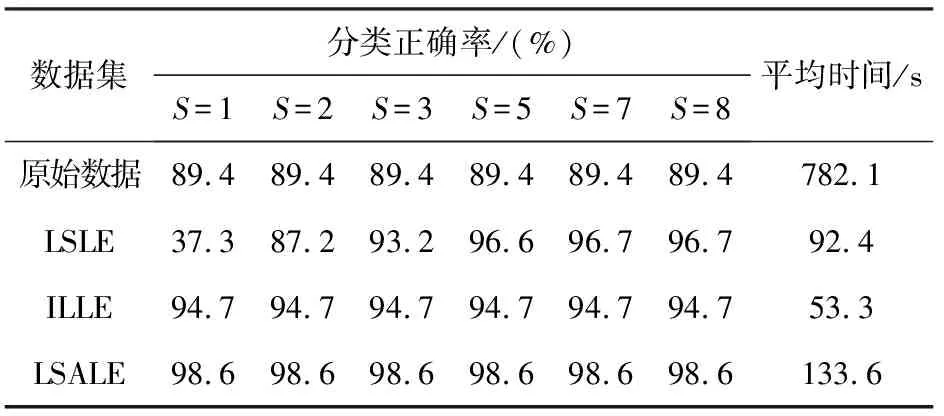
表1 MNIST数据实验

表1中，LSLE稀疏度需要手动调整达到最优解，难以应用实时动态系统中，而LSALE降维稀疏度是自适应的，通过自身迭代选择出最适合的近邻点数目，达到稀疏降维的目的。与同为自适应领域选择的ILLE算法对比，LSLLE的数据具有更好的分类效果。MNIST原数据识别率很高，但训练与测试速度都很慢，LSALE降维后的数据不仅提高了识别率，同时缩短了运行时间。相比于LLE、LSLE、ILLE算法，LSALE能够自动选择每一个样本近邻点的稀疏度，得到更高的分类正确率，从而表明稀疏自适应方法的合理有效。

4 结语

自适应局部稀疏嵌入降维算法，根据样本点和近邻矩阵重构出近邻点的权重矩阵，避免了求权重矩阵的逆运算，提高了降维的有效性。该方法自适应选取近邻点，优化了邻域大小，保留了更多的局部结构信息。实验结果表明，LSALE算法的分类正确率均高于LLE、LSLE和ILLE等降维算法，同时也缩短了运行时间。