基于改进Armstrong模型的网贷平台定价

王宏涛, 张 露

(西安邮电大学 经济与管理学院， 陕西 西安 710121)

P2P(peer to peer)网络借贷[1]是指个人之间通过第三方平台进行小额的借贷交易，其中借出资金的个人为投资用户，借入资金的个人为借款用户，第三方平台为网络借贷平台。网络借贷简称网贷，网贷平台定价分析[2]是指网贷平台根据用户规模和用户的历史交易行为，分析如何定价才能使平台利润最大化。网贷平台作为一种新型金融模式，有助于满足民间个人的小额借贷需求。合理定价是网贷平台可持续发展的基础，可以帮助网贷平台扩大用户规模，获取最大利润，提高经营与发展能力[3]。

目前关于网贷平台定价方面的研究可以分为以下两个方面，第一，通过构建定价模型研究网贷平台定价。文献[4]建立了竞争条件下的网贷平台定价模型来分析网贷平台定价，得出平台对投资用户定价低于平台对借款用户定价，平台可通过定价来控制平台用户规模，但没有考虑垄断条件下的网贷平台定价[5]。文献[6]通过构建基于新巴塞尔协议的RAROC(risk adjusted return on capital)模型来研究网贷平台定价，得出此模型有利于提升网贷定价质量，但没有考虑用户质量对平台最优定价的影响[7]。第二，从网贷利率的影响因素方面研究网贷平台定价。文献[8]利用某网贷平台数据追踪的实证分析，指出网贷利率的重要影响因素为借款用户的行为以及借款用户的信用风险，但没有考虑借款用户的身份认证、工作认证等认证信息对网贷利率的影响[9]。文献[10]对网贷利率的风险溢价研究发现，只将资金借给信用评级最高的借款用户是防范借款用户质量问题发生的最好方法，但没有发现制定合理的网贷利率是控制借款用户质量问题的重要手段[11]。

网贷平台是一个典型的双边市场[12]，其两边的借款用户和投资用户规模之间相互促进，价格制定具有非对称特征[13]。借款用户和投资用户之间存在网络外部性，为了实现平台利润最大化，平台可能会对一方用户进行价格补贴来促进另一方用户规模的增长。由于间接网络外部性[14]的存在，网贷平台一边用户规模的增长会使另一边用户获益，导致其规模随之增加，为使网贷平台利润最大化，平台通常对投资用户制定低价格来促进借款用户规模的增长。Armstrong模型[15]运用双边市场理论建立了垄断条件下的双边市场平台定价模型，分析平台的最优定价，从理论上解释了为什么不对称定价和补偿定价策略有利于平台的经营与发展，可以应用到网贷平台中。该模型没有考虑借款用户质量，不同质量的借款用户对平台定价产生不同的影响，该模型会导致网贷平台定价分析出现偏差[16]。Armstrong模型没有考虑借款用户的质量水平。而借款用户质量是网贷平台生存和发展的关键要素之一。

考虑到借款用户质量对网贷平台定价的影响，本文拟在Armstrong模型中引入不同质量借款用户的间接网络外部性，基于双边市场理论通过对模型求导计算用户效用与平台利润最大化的关系，得出网贷平台的最优定价，然后通过最小二乘法[17]，构建网贷利率多元回归模型，得到因变量与自变量的相关参数，用实例来验证模型的有效性。

1 基于Armstrong网贷平台定价

Armstrong模型中包含平台两边用户的规模、间接网络外部性、用户价格和平台利润等，通过求导计算得出用户效用与平台利润最大化的关系，制定网贷平台对双边用户的最优价格。

假设垄断平台两端连接着用户1和用户2，且平台对双边用户的定价为仅收取注册费。用户1效用u1和用户2效用u2的函数[18]分别为

u1=α21n2-p1,
u2=α12n1-p2。

(1)

式中α21为用户2产生的间接网络外部性，n2为用户2的人数，p1为平台对用户1的定价，α12为用户1产生的间接网络外部性，n1为用户1的人数，p2为平台对用户2的定价。平台利润[18]为

π=(p1-f1)n1+(p2-f2)n2。

(2)

式中f1为平台用户1付出的平均成本，f2为平台用户2付出的平均成本。

对式(2)中的双边用户数量分别用其效用函数表示[13]，即

n1=φ1(u1),n2=φ2(u2),

φ1(u1)为用户1的效用函数，φ2(u2)为用户2的效用函数。为求平台利润的最大值，式(2)分别对u1和u2求一阶偏导数，且令

(3)

式中φ′1(u1)为用户1效用函数的导数，φ′2(u2)为用户2效用函数的导数。

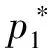
α21φ1(u1)>α12φ2(u2)。

令用户1对平台的价格弹性

λ1=p1φ1(u1)/φ′1(u1)，

可得

λ1/p1=φ1(u1)/φ′1(u1)，

其中，φ1(u1)/φ′1(u1)表示用户1价格弹性系数；用户2同理。假定

φ1(u1)/φ′1(u1)=φ2(u2)/φ′2(u2)，

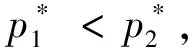
Armstrong模型应用到网贷平台可以得出，当网贷平台利润最大化时，对借款用户的最优定价为平台对借款用户付出的成本，减去投资用户间接网络外部性影响，加上借款用户价格弹性系数值。平台对投资用户的最优定价同理。一般而言，网贷平台对借款用户付出的成本要高于对投资用户付出的成本，网贷平台需要对借款用户多付出信息审核的成本，网贷平台会对投资用户定低价格。相对于投资用户为满足利息需求而借出资金，借款用户为了生产与生活对贷款的需求更强，投资用户对借款用户的效用大于借款用户对投资用户的效用。假定投资用户价格弹性的系数值大小等于借款用户价格弹性系数值，由式(3)的分析可知，网贷平台对投资用户定价小于网贷平台对借款用户定价。

Armstrong模型没有考虑借款用户质量，借款用户质量会影响网贷平台的最优定价[19]，从而影响平台的经营与发展。借款用户质量问题是导致近年来网贷问题平台数量持续增加的首要原因之一，严重影响网贷行业的健康发展[20]。为提高网贷平台生存与发展能力，借款用户质量是考虑的关键问题。由此构建改进的Armstrong定价模型。

2 改进Armstrong模型的定价

2.1 改进的Armstrong模型

假设整个网贷市场中只有一个垄断平台，双边用户总规模都为1，借款用户和投资用户对平台服务的偏好都在[0,1]上均匀分布，平台对双边用户的定价为只收取注册费，仅考虑不同质量用户的间接网络外部性，且假定借款用户质量越高，其网络外部性越大。定义高质量借款用户为信用等级高、逾期次数低的用户，否则为低质量借款用户。

基于上述假设，借款用户效用ue和投资用户效用ur的函数[21]为

ue=αrenrs-pe,

(4)

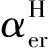
两边用户进入平台的充要条件为，各自所获得效用大于等于0，当用户所得效用为0时，用户进入与不进入平台无差异。假设s′为借款用户效用无差异点，t′为投资用户效用无差异点。当s′≤s≤1时，借款用户愿意接入平台，即借款用户数量ne可用1-s′来表示；当t′≤t≤1时，投资用户愿意接入平台，即投资用户数量nr可用1-t′来表示。则网贷平台利润πp为

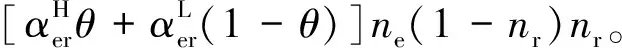
(5)

为求网贷平台利润的最大值，将式(5)分别对ue和ur求一阶偏导数，且令

(6)

2.2 借款用户不同质量对平台定价的影响

针对网贷平台定价模型中借款用户质量水平的不同，从不同质量水平借款用户的间接网络外部性和借款用户质量水平变化考虑网贷平台定价。

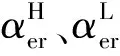
(7)

对式(7)进行分析。因为

所以

表明平台对借款用户的定价随着借款用户间接网络外部性增加而降低。

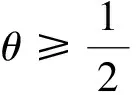
同理可知

表明平台对投资用户的定价随着借款用户间接网络外部性增加而提高。

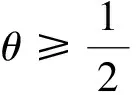
小结1平台利润最大化时，平台对一边用户定价受本边用户产生的间接网络外部性负向影响，而受另一边用户产生的间接网络外部性正向影响。当平台为高质量借款用户聚集平台时，高质量借款用户间接网络外部性对平台定价起主要影响。

(2)考虑借款用户质量水平的变化。网贷平台不仅要重视用户规模的增长，也要重视用户质量水平的变化。将式(6)分别对θ求偏导数得

(8)

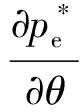
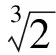
3 实证分析

采用最小二乘法，对网贷平台现实交易数据进行处理，构建多元回归实证模型对交易数据进行回归分析，通过多种回归分析结果选择最稳健的回归。利用最稳健回归结果中借款用户质量，对网贷平台定价的影响系数分析，制定网贷平台定价策略。

3.1 构建实证模型

模型的被解释变量为平台对借款用户定价即网贷利率，解释变量为借款用户信用等级、逾期次数，控制变量为借款相关信息、借款用户相关信息。第i个借款用户的借款利率[22]Ri为

Ri=β0+β1Ci+β2Ni+β3Xi+δi。

(9)

其中β0为常数，β1为借款用户信用等级对利率的弹性，Ci为第i个借款用户信用等级，β2为借款用户逾期次数对利率的弹性，Ni为第i个借款用户逾期次数，β3为控制变量对利率弹性，Xi为第i个借款用户的其他影响网贷利率的控制变量，δi指的是第i个借款用户的网贷利率的随机误差项。

3.2 变量选取与数据来源

根据文献[9]构建了包括被解释变量、解释变量和控制变量的指标体系，具体变量如表1所示。

表1 变量赋值及定义

因为人人贷成立于2010年，成立时间早且综合实力位于网贷行业前列，具有代表性，所以选择使用人人贷的实际数据[23]对实证模型进行回归。实际数据来源于人人贷官方网站[23]2017年实际发生的17 544个借款项目。

对表1中各变量的具体数据进行统计，统计值包括均值、标准差、最小值和最大值，变量的描述统计如表2所示。

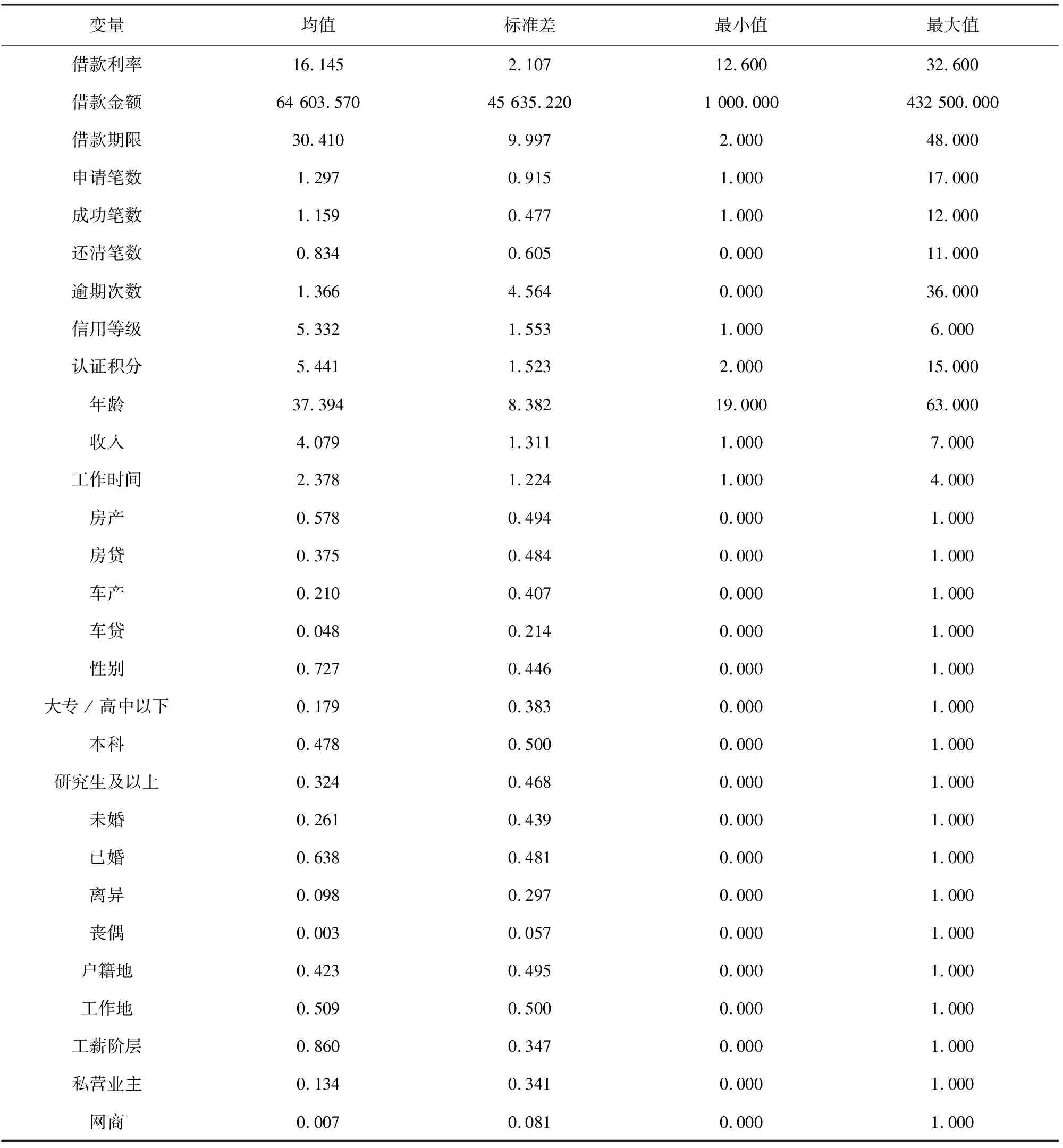
表2 变量的描述统计

从表2中可以看到，借款用户信用等级的均值为5.332，逾期次数的均值为1.366次，可知平台中信用等级高的用户较多，平台中借款用户的逾期次数较少，属于高质量用户占比高的平台。借款利率金额均值为64 603.570元，可知平台成交量较大。借款用户的收入虚拟变量均值为4.079元，说明大多借款用户收入在10 000～20 000元之间。已婚借款用户虚拟变量均值为几种婚姻状况里最高的约为0.638，说明大多借款用户为已婚状态。借款用户性别虚拟变量均值约为0.727，说明大多借款用户为男性。

3.3 基本回归分析

为了控制模型中异方差引发的估计偏差，使回归更加稳健，并考虑模型中解释变量信用等级可能存在的内生性问题，避免工具变量无效可能导致的估计结果偏误。对网贷利率模型进行最小二乘法的基本回归估计，分析借款用户质量对网贷平台定价的影响。首先进行稳健最小二乘法估计和加权最小二乘法估计。其次，用认证积分和有无房产作为工具变量分别进行两阶段估计与广义矩估计。若球形扰动，则优先选择两阶段估计，若球形扰动项存在异方差或自相关，则优先选择广义矩估计[24]。最后，对所选取的工具变量的有效性进行检验。基本回归结果见表3。

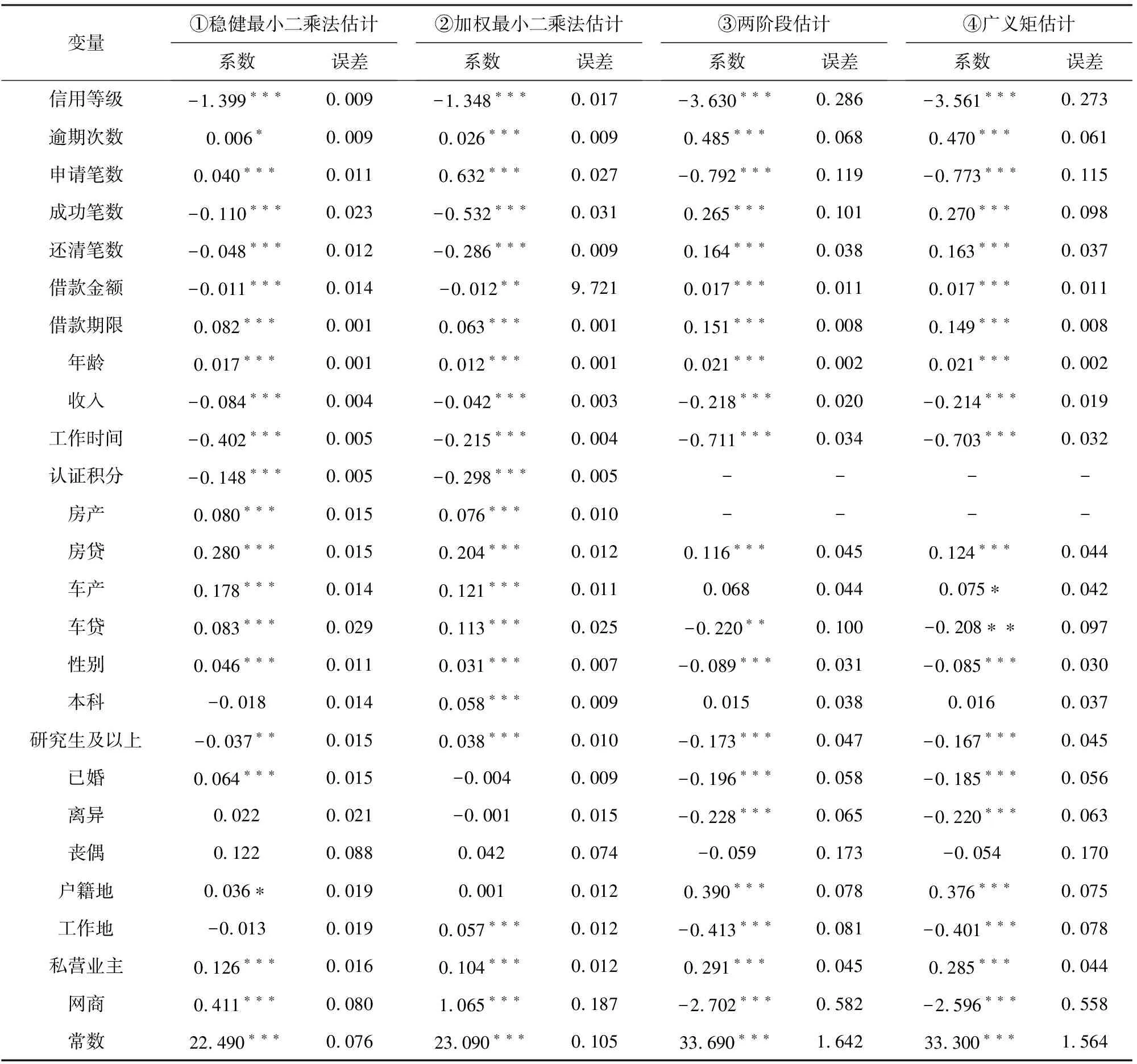
表3 基本回归结果

注:***代表估计结果在 1%水平上显著，**代表估计结果在5%水平上显著，*代表估计结果在10%水平上显著。

由表3可知，回归①中信用等级的影响系数显著为-1.399和回归②中信用等级的影响系数显著为-1.348，说明了信用等级负向影响网贷平台定价。回归①和回归②虽然控制了异方差，但没有解决内生性问题，因此选择了回归③和回归④。回归③和④的结果相似，只存在细微差别，如回归③中信用等级的系数为-3.630，回归④中信用等级的系数为-3.561，回归③中逾期次数的系数为0.485，回归④中逾期次数的系数为0.470，因此最终选择两阶段估计。

回归③中，信用等级的系数值在1%水平下为-3.630，说明借款用户信用等级增加1%其定价将减少3.63%，即借款用户信用等级负向影响借款用户定价。逾期次数的系数值在1%水平下为0.485，说明借款用户逾期次数增加1%其定价将增加0.485%，即借款用户逾期次数正向影响借款用户定价。借款金额的系数值在1%水平下为0.017，说明借款用户的借款金额增加1%，其定价将增加0.017%，即借款金额正向影响借款用户定价。借款期限系数值在1%水平下为0.151，说明借款用户的借款期限增加1%，其定价将增加0.151%，即借款期限正向影响借款用户定价。其他因素包括年龄、收入、性别、工作时间、房贷、车贷、教育、婚姻、所在是否高收入城市、工作性质等也会影响平台借款用户定价。其中变量如“本科”为不显著，表示相对于参照组“大专/高中以下”组间无显著差异，而不是与平台定价无关。

结果表明，借款用户质量负向影响平台对借款用户定价，借款用户质量越高即借款用户信用等级越高、违约次数越低，平台对借款用户定价越低。人人贷平台作为高质量用户聚集平台，网贷平台定价主要受高质量用户的影响。借款用户的信用等级每增加1%，网贷平台对其定价随之降低3.63%；借款用户的逾期次数每减少1%，网贷平台对其定价随之降低0.485%。

为了证明工具变量的有效性、工具变量与扰动项不相关、不存在弱工具变量，分别进行“杜宾-吴-豪斯曼”[24](Durbin-Wu-Hausman，DWH)检验、过度识别检验和弱工具变量检验[24]。工具变量检验结果见表4。

表4 工具变量检验

表4中回归③和④的DWH检验的统计量P值均为0.000，即均在1%的水平上显著，强烈拒绝不存在内生性的原假设，故需要解决利用工具变量信用等级的内生性问题。回归③和④的过度识别检验结果中统计量P值均约为0.700，接受工具变量为外生的原假设，说明选的工具变量和回归方程的扰动项不相关，满足工具变量的外生性条件。回归③和④的弱工具变量检验结果中统计量P值均为0.000，表明工具变量是有效的，不存在弱工具变量。工具变量检验结果说明所选取的工具变量是有效的。

3.4 工具变量分位数回归

为检验基准回归分析结果，使用工具变量分位数回归，得出重要解释变量影响不同数值分位处借款利率的差异，消除极端值的影响，检验回归结果的稳健性。工具变量分位数回归见表5。

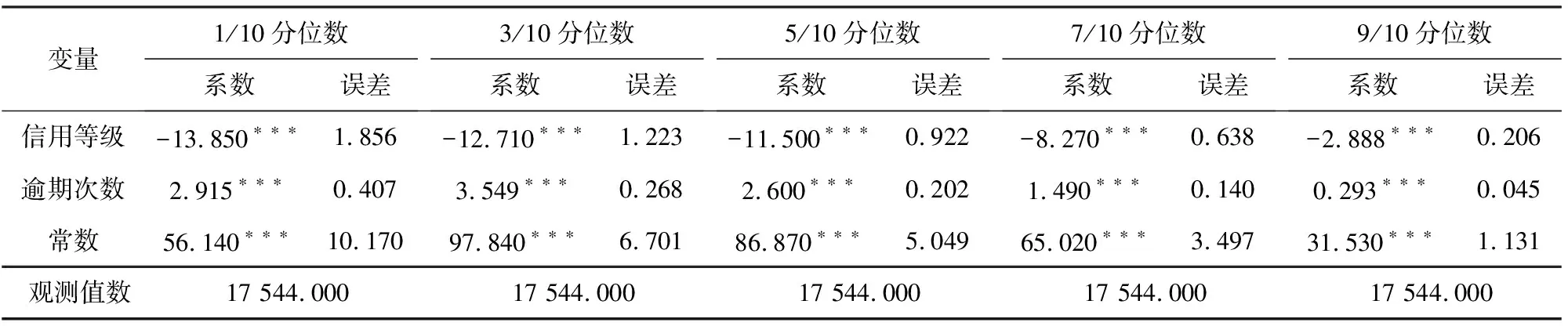
表5 工具变量分位数回归

注:***代表估计结果在 1%水平上显著，**代表估计结果在5%水平上显著，*代表估计结果在10%水平上显著。

由表5可知，1/10分位数处，信用等级的系数为-13.850且在1%水平上显著，表明借款用户信用等级负向影响平台对借款用户定价，逾期次数的系数值为2.915且在1%水平上显著，表明借款用户逾期次数正向影响平台对借款用户定价。3/10分位数处，信用等级的系数为-12.710；5/10分位数处，信用等级的系数为-11.500；7/10分位数处，信用等级的系数为-8.270；9/10分位数处，信用等级的系数为-2.888。可见随着借款利率分位数增加，信用等级的系数均为负且绝对值越来越小，说明借款利率越高，信用等级对其影响越小。随着借款利率分位数增加，借款用户逾期次数的系数均为正，且绝对值从3.549到0.293有减小的趋势。解释变量与控制变量对借款利率的影响系数都显著，验证了基准回归分析的结果，而且这些影响系数的大小和差距有所不同。

4 结语

为了对网贷平台定价，运用双边市场理论，引入不同质量水平借款用户的间接网络外部性，改进Armstrong定价模型，利用该模型计算用户效用与平台利润的最大值，从中得出网贷平台对借款用户与投资用户的最优定价，分析借款用户质量与网贷平台对双边用户定价的关系，采用最小二乘法，对多种回归进行比较选择最优回归，通过最优回归估计结果中解释变量的影响系数，验证借款用户质量会影响网贷平台定价。结果表明，网贷平台定价时需要考虑借款用户质量的影响。具体表现为网贷平台对借款用户定价受不同质量借款用户网络外部性负向影响，对投资用户定价受不同质量借款用户网络外部性正向影响。网贷平台对借款用户定价与高质量借款用户占比呈负向相关，对投资用户定价与高质量借款用户占比呈正向相关，高质量借款用户占比降低时，平台将提高对借款用户定价同时降低对投资用户定价；占比升高时，平台将降低对借款用户定价同时提高对投资用户定价。

根据研究结果提出建议，网贷平台应提高平台借款用户质量水平。对新进入平台的借款用户定高价，提高进入门槛，鼓励高质量用户进入，后期根据借款用户行为表现变更信用等级，信用等级越高的借款用户定价越低。为了提高高质量借款用户占比，网贷平台应该根据借款用户质量水平变化灵活定价，当平台现有借款用户质量降低时，应提高对借款用户定价，同时降低对投资用户定价；当借款用户质量提高时，降低对借款用户定价，同时提高对投资用户定价。