基于自适应随机共振高频微弱信号检测

郑文秀, 吕 航

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

噪声通常会降低信号的信噪比，在信号处理中被认为是有害的，因此，信号处理中都会压制噪声。但是，当重度背景噪声中嵌入的弱信号进入某些非线性系统时，噪声能量可能会随噪声的协同效应传递给信号，随机共振[1](stochastic resonance ，SR)现象。从而提高系统输出信噪比[2](signal-noise ratio，SNR)。

绝热近似理论是随机共振一种常用方法，在一定程度上揭示了非线性条件下噪声产生的各种效应。然而，绝热近似理论仅适用于小幅度、小频率、小噪声弱小参数信号[3]，实际上大频率、强噪声的大参数信号[4]。也是一种较常见的情况。对大参数周期信号，文献[5]采用二次采样方法通过谱搬移到低频信号谱区间，使之发生随机共振现象。文献[6]通过对大参数周期信号采用参数归一化的方法[7]，产生了随机共振的现象。该方法相比谱搬移的方法，省去了在信号恢复时又要将信号谱搬移回去的过程。

考虑到小信号情况下，文献[8]将遗传算法应用于随机共振研究，自适应地实现了最佳信号信噪比。本文拟对大参数周期信号的自适应随机共振进行研究，先利用参数归一化对大信号进行预处理，再将随机共振输出信号信噪比作为目标函数，采用鱼群算法自适应地调整随机共振系统的系统参数，以期达到随机共振输出信号信噪比的优化。

1 随机共振概述

1.1 典型随机共振模型

在随机共振应用中，Langevin模型[2]最常用一种模型，可以表示为

(1)

式中x为系统输出，x′代表系统输出x对时间的一阶导数，a、b分别为双稳系统的结构参数，s(t)=Acos(2πf0t+φ)为特征输入信号，n(t)为噪声，〈n(t)〉表示噪声的统计平均值，ξ(t)表示均值为0且方差为1的高斯白噪声，D为噪声强度，势函数

系统输出x的概率分布函数ρ(x,t)遵循福克-普朗克方程(Fokker-Planck equation)[3]

(2)

式中，初始条件为

ρ(x,t0|x0,t0)=δ(x-x0)。

1.2 近似绝热理论

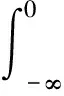
且满足如下关系

p1(t)+p2(t)=1。

当输入信号频率f≪1即较低时，可以采用绝热近似理论，近似地认为系统在这两个吸引域内达到局部平衡所需要的时间，远远小于吸引域之间概率整体平衡所需要的时间，也远小于系统跟随输入信号变化所需要的时间。

当只有噪声作用而不存在周期激励时，质点在两个肼势间按Kramers跃迁率[9]rk进行跃迁

1.3 参数归一化的随机共振

绝热近似理论是在输入信号满足f≪1，A≪1即在小参数微弱信号条件下假设成立的。在实际中，信号频率f往往远高于1Hz，输入信噪比较低，对于这类微弱大参数信号[6]，不满足绝热近似调解。为此，进行参数归一化处理，使其满足绝热近似条件。

(3)

其中

由Kramers跃迁率[9]可知，经过参数归一化后，对于频率f′0只要满足0≤f′0≤0.1125a，就可能产生随机共振。因此，通过参数归一化处理后，信号发生随机共振现象的频率范围得到了扩展，使得大信号随机共振成为可能。

2 自适应大参数信号随机共振

适当的选择参数a和b，可以产生大参数信号随机共振。考虑到参数a影响产生随机共振的频率f′0，b只影响信号幅度A′。归一化参数只是使得大参数信号可以产生随机共振现象，不能保证随机共振输出信噪比达到一个最佳的状态。也就是说，随机共振的输出信号信噪比不能自适应调整参数，以使得信噪比最优。

为了使得随机共振的输出信号最优信噪比的自适应，本文采用人工鱼群算法[10](artificial fish swarm algorithm)，可以使系统动态调整参数a、b，使得每次的输出信号SNR达到最优[11-12]。

2.1 人工鱼群算法

人工鱼群算法是一种基于动物行为优化的智能算法，分别模仿了鱼群的觅食、聚群、追随行为过程。

觅食行为过程是指鱼群在水中随机移动，当发现食物时，会一直向着食物浓度高对的方向移动。聚群行为过程是所有鱼都会自发地朝着食物浓度高的方向移动。追尾行为过程在鱼群中的一条或者几条发现食物时，其临近的鱼会尾随到达食物点。

2.2 基于人工鱼群的自适应算法

考虑到输出信噪比是衡量随机共振现象的一种常用的度量，将随机共振系统的输出SNR作为人工鱼群算法的目标函数，然后，利用鱼群算法优化随机共振系统输出SNR。信号信噪比的定义为输出信号频率处功率谱幅值与同一信号频率处噪声平均功率之比[11]，其表达式如下

式中S(f0)是信号功率谱在f′0处的功率谱值，N(f0)是噪声功率谱的平均功率。

自适应归一化随机共振的实现具有如下步骤。

2)将每次鱼群觅食得到的二维位置信息(Xi,Yi)看作随机共振系统参数(a,b)，设置鱼群最大觅食范围(X,Y)。以随机共振的输出信噪比作为鱼群觅食的食物浓度，鱼群在范围内进行觅食、聚群和追随行为。

3)进行一次鱼群过程，计算随机共振输出信噪比,并记录当前a、b的值和当前信噪比值；

4)鱼群尝试新的参数a、b值进行下一次鱼群过程得到的新的信噪比，与当前记录的信噪比进行比较，如果新的信噪比大于当前信噪比，则记录新的信噪比值作为当前信噪比，并更新a、b的值；

5)如此循环直到得到最大的信噪比值。

6)记录当前信噪比值和当前参数a、b则为共振系统(SR)的最优信噪比和最优参数。

自适应归一化随机共振算法流程如下。

图1 自适应归一化随机共振算法流程

3 仿真结果分析

假设信号频率包含f0= 1 000 Hz和f1=0.1 Hz两个频点，采样频率fs=500 kHz，采样点数N=16 384点，特征输入信号s(t)=0.5cos(2πf0t)+0.1cos(2πf1t),其时域和频域如图2所示。

(a) 时域波形

(b) 频域波形

加入噪声强度D = 0.31的高斯白噪声，随机共振的输入信号s(t)+n(t)的时域和频域如图3所示。

(a) 时域波形

(b) 频域波形

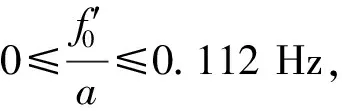
对比图3和图4的结果，可以看出，图4(a)信号周期性更加明显；图4(b)信号频域的幅值也大于图3(b)。说明利用参数归一化方法，可以实现大参数信号的随机共振。

(a) 时域波形

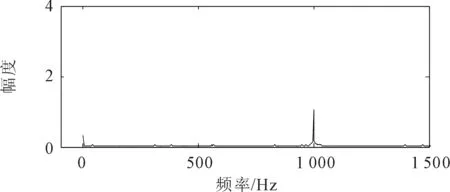
(b) 频域波形

根据仿真数据计算出相应信噪比。在图3中，频率f1的信号输出信噪比约为-27.3 dB，频率f0的大参数信号输出信噪比为-13 dB；在图4中，参数随机共振，频率f1的小信号输出信噪比约为-16.9 dB，频率f0的大参数信号输出信噪比为0.5 dB。可以看出，频率f1小参数信号和f0大参数信号的信噪比分别提高了10.4 dB和12.5 dB。

利用鱼群算法实现随机共振输出信噪比最佳的自适应的结果如图5所示。

(a) 时域波形

(b) 频域波形

比较图4、5，可以看出，自适应的随机共振输出信号的时域波形图5(a)，相比于图4(a)具有更明显的周期性。对比频域，图5(b)中特征信号的频率f0和f1幅值都相比图4(b)对应值更大。进一步计算可以得到，图5中频率f0的输出信噪比为1.6 dB，相比图4中参数a=b=10 000时，进一步提高了1 dB。频率f1的输出信噪比为-14.5 dB，信噪比提高了2.4 dB。由于鱼群算法遍及了所有参数，图5的结果是最优的。可见，利用鱼群算法能够得到大信号的随机共振输出信噪比最优。

参数归一化的随机共振克服了随机共振对输入信号满足绝热近似条件的要求，使得大参数信号也能产生随机共振现象。结合鱼群算法实现了自适应的最佳信噪比输出。

4 结论

通过将参数归一化随机共振与鱼群算法结合，达到了自适应的调节随机共振系统参数使得随机共振系统输出信噪比达到最优。利用参数归一化方法，可以使随机共振适用于大参数信号；利用鱼群算法能够实现随机共振最优信噪比输出的自适应。相对于大参数信号的随机共振谱搬移的方法，本文的方法既考虑大参数的随机共振问题，又考虑了参数优化问题。因此，本文的方法，可以直接应用任意频率下的微弱信号的检测。