基于修正Iwan模型的铁路基床动力湿化特性研究

冯怀平, 韩博文，宋慧来，常建梅，应志超

(1. 石家庄铁道大学 土木工程学院，河北 石家庄 050043；2. 神华包神铁路集团有限责任公司 安全质量部，内蒙古 包头 014014)

重载铁路运输是我国货运的主要的方式，近年来为提高货运能力，我国加快了重载铁路的扩能改造建设，然而，沿线地形条件复杂、填筑情况多变[1]，路基病害频发成了制约扩能改造的主要原因。铁路基床是承受和传递列车动载的关键结构，轴重增加后，基床会承受更大的动力响应，对于路堑、站场等排水不畅路段，如基床填料不良，在降雨及冻融季节路基病害极易发生[2-3]。因此，研究循环荷载和湿化耦合作用下基床土体的变形特性，正确认识其变形规律对提高重载铁路长期服役性有至关重要的作用。此外，建立一个考虑循环荷载和湿化耦合的土体变形计算模型对于科学有效地预测铁路基床长期服役下的平顺性有重要价值。

研究者对土体湿化变形特性进行了研究，魏松等[4-5]研究了应力水平对湿化变形的影响；刘新喜等[6-10]对土体初始状态包括压实度、初始含水率、基质吸力等湿化变形的影响进行了研究。另一方面研究表明，循环荷载作用下土体的动力特性因素主要有加载频率、围压、排水条件、加载波形、间歇性振动等。宫全美等[11]认为铁路基床的长期沉降主要受路基质量、动荷载、浸水的影响；蔡袁强等[12]研究表明粗粒料的累积变形在高循环应力比下随加载频率的增加显著增大，在低循环应力比下受加载频率的影响较小；冷伍明等[13]发现大围压或减小动应力有助于增强土体稳定；郭林等[14]对不同围压下的温州结构性软黏土的应变特性进行研究，发现围压较低时，土体的结构性在固结过程中没有或很少被破坏，归一化程度较高，随着围压的升高，归一化程度降低；曹勇等[15]分析了不同循环加载波形下软土的动力特性与变形特性，发现小于临界状态时波形的影响不大，大于临界状态时波形影响较大，方形波的影响最大；王军等[16]进行了分阶段加载条件下温州饱和软黏土孔压和应变发展规律研究，结果表明，一定时间的振动和停振后，由于土体动力特性发生了改变，后续阶段的残余应变将变小。综上所述，尽管针对湿化或者循环动荷载作用下土体变形特性展开了较为深入的研究，但是研究浸水与循环荷载联合作用对土体动力湿化变形的影响较少。考虑到铁路路基基床变形多数情况下是湿化与循环荷载共同作用的结果，冯怀平等[17]基于双线法研究了重载铁路基床的动力湿化特性，并考虑单线法能较真实反映土体实际浸水情况，认为有必要采用单线法对基床土体的动力湿化特性进一步研究。

路基土体变形预测对于研究路基长期稳定性及扩能改造有重要意义，很多研究者提出相应计算模型，主要涉及对本构模型、应力-关系模型、累积变形模型或经验公式、软化模型、骨干曲线模型等方面的研究。黄茂松等[18]提出循环荷载下非饱和结构性土的边界面模型；李校兵等[19]研究了循环围压对饱和软黏土动模量衰减规律的影响，提出考虑变围压因素的饱和软黏土等效线性本构模型；Iwan[20-21]提出能够反映土体弹塑性的Iwan模型，为研究土体的应力-应变关系及滞回曲线奠定了基础；刘莹等[22]在Hardin-Drnevich 等效非线性模型的基础上，建立了考虑循环弱化的饱和黏土简化非线性模型描述循环加载下饱和黏土的应力-应变关系，蔡袁强等[23]研究了基于Iwan模型的软黏土动应力-应变关系，提出修正Iwan模型；王军等[24]研究了基于Masing准则的软黏土动应力-应变关系；多位研究者[25-27]通过试验和计算提出了反应土体累积变形的模型及经验公式；周建等[28]研究了循环荷载作用下土体的应变软化特性，提出反应土体应变软化模型。然而，考虑动力作用下湿化变形的模型有待进一步研究，为更好对重载铁路基床的变形进行预测，有必要研究动力湿化的计算模型。

本文利用动三轴仪，对包神铁路瓷窑湾站某病害段的基床土样进行了基于单线法的动力试验，研究土体动力作用下湿化变形特性，揭示了基床湿化的敏感性因素，结合试验结果拟合出累积塑性应变模型和应变软化模型，并用塑黄铁路原平工务段的实测数据验证了模型，为预测基床变形和既有线扩能改造的可行性提供有价值的借鉴。

1 动三轴试验

1.1 土样基本物性参数

试验土样取自包神铁路瓷窑湾站现场病害严重路段，瓷窑湾站位于陕西神木县大柳塔镇，地形起伏破碎，冲沟发育。站场于1989年5月竣工，随着后续生产力的提高，2004年4月至2005年5月进行了扩能改造。基床底部的煤矸石抗水性能差，遇水易变软，在列车晃动的时候容易产生“挤浆”现象，造成线路板结、翻浆冒泥，见图1。

图1 基床底部翻浆冒泥

将病害现场土样取回并进行基本物性试验，具体参数见表1。

表1 试样物理参数

1.2 试样制备

将土样过筛去除草根等杂物，配制成含水率为10%的土样，静置一夜后按照不同干密度进行制样，在制样器内分4层击实，同一组试样的密度差不得超过0.02 g/cm3。

1.3 试验仪器

本试验采用动三轴仪结合可自行补水的常水头马氏瓶进行实时补水，见图2。常水头马氏瓶通过与动三轴仪底部振动台的底部连通实现试验浸水，且保证常水头马氏瓶的开口略高于试样底部，以保证在恒定水头差下实现自由补水，模拟雨水入渗过程。

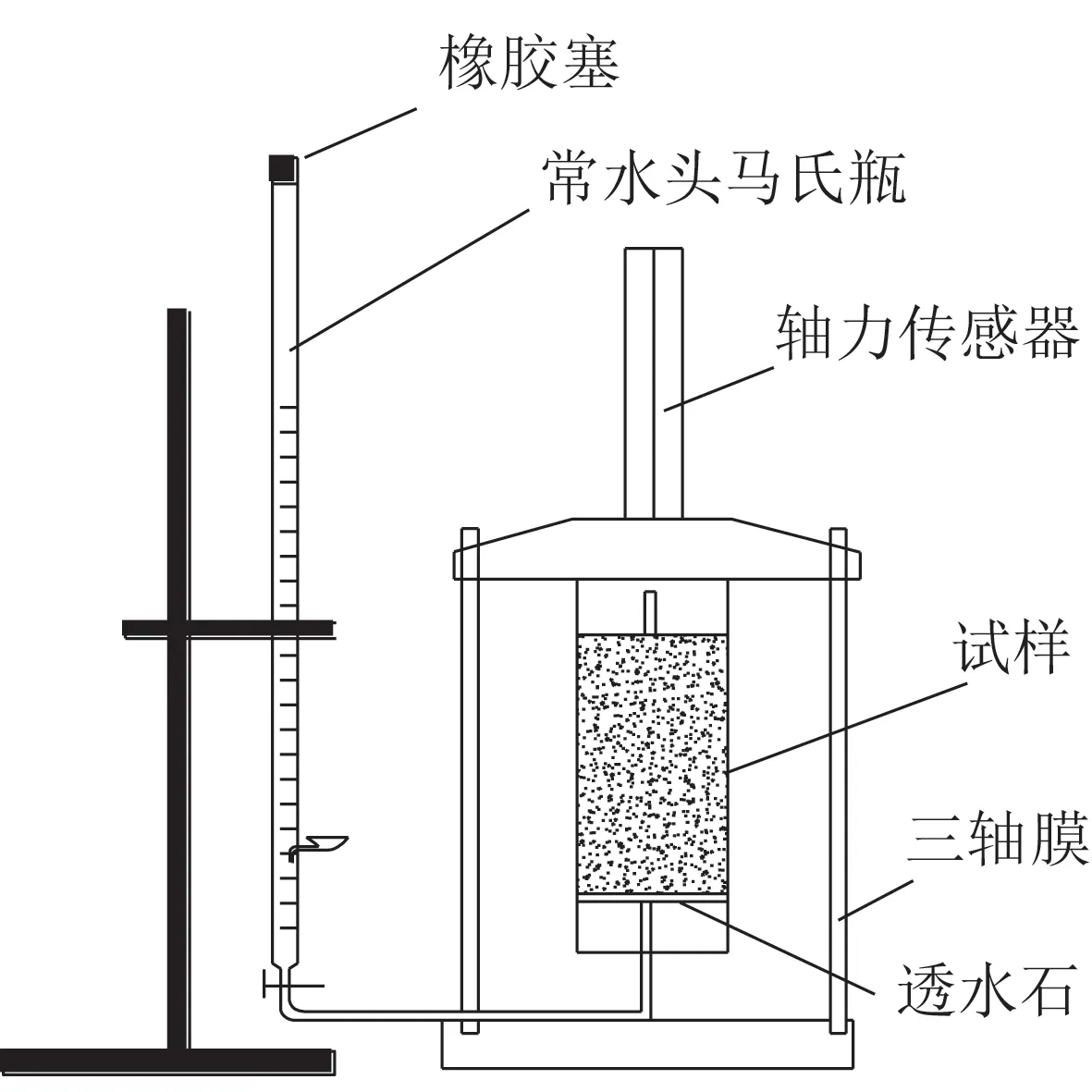
图2 试验仪器立面

1.4 试验方案

基床在扩能改造后受到更大的动载作用，并且降雨作用使路基土湿化，动载与降水的共同作用使基床更容易产生巨大变形。因此，本试验充分考虑基床扩能改造与雨水入渗的耦合作用，在更贴近实际情况的试验环境下进行基床变形特性的研究。试验土样取自现场病害路段，将土样进行不同动应力幅值的动力湿化试验。该地区长期开行C80列车，车辆全长12 m，列车运营速度100 km/h，其加载到地基上的频率计算式为

f=v/l

(1)

式中：v为列车速度；l为车辆全长。

根据式(1)，计算出加载到路基上的频率约为2.5 Hz。因此，设置试验加载频率为2.5 Hz，扩能改造前轴重为25 t，依据现场动态试验检测结果，确定以90 kPa半正弦波加载波形模拟[29]，本试验设置4个动应力幅值，分别为90、100、110、120 kPa，反映实际扩能改造前后轴重的变化。整个试验过程分为三个阶段：第一阶段为前期固结阶段，使土样在恒定压力下达到固结稳定，排除因固结不充分导致的变形；第二阶段为动力稳定阶段，经过大量试验，发现在恒定动应力幅值下振动1 000次足够使土样达到稳定，排除因未达到动力稳定而导致的变形；第三阶段为动力湿化阶段，在动载和补水双重作用下进行试验。此过程反映了基床在受到降水入渗前已经在列车动载下达到稳定，降雨后则是在动载与浸水联合作用下继续发生变形，符合实际工程现状。试验的加载过程见图3，试验参数见表2。试验完毕后利用计算机收集试验数据，并绘制应力-应变关系曲线。

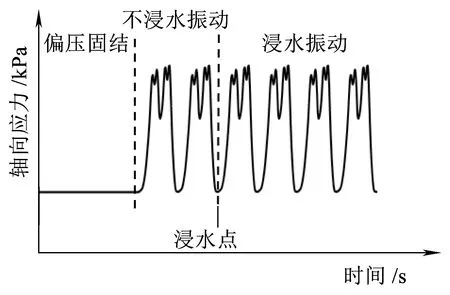
图3 试验加载过程示意

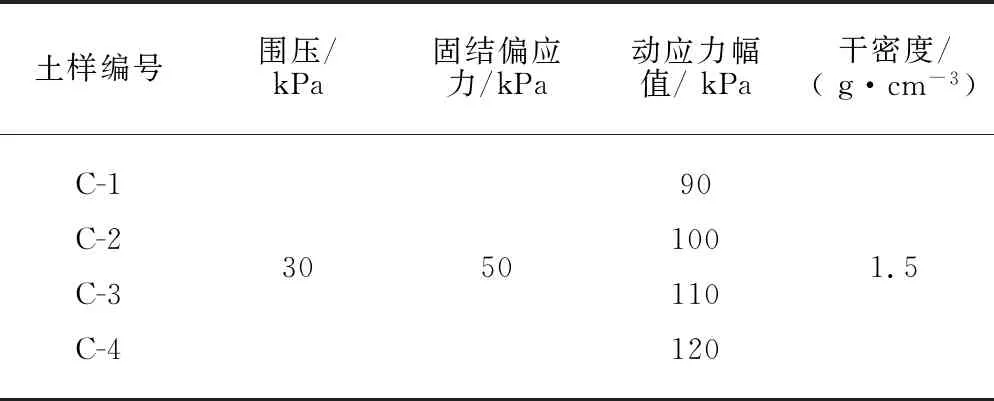
土样编号围压/kPa固结偏应力/kPa动应力幅值/kPa干密度/(g·cm-3)C-1C-2C-3C-43050901001101201.5

1.5 试验结果与分析

1.5.1 累积变形随循环加载次数变化规律

整个试验过程以及浸水后的累积变形与循环加载次数关系曲线见图4。由图4(a)可见，1 000次动载后开始浸水，整体的累积塑性应变随动应力幅值的增加而增加，浸水后应变有明显增加趋势，振动10 000次之后增长趋势放缓，应变逐渐趋于稳定。图4(a)中存在一个异常点，可能是由于制样时存在一定缺陷导致土样在湿化某一瞬间产生突变。为更直观反映动力湿化过程的累积变形，绘制浸水后累积应变与循环加载次数关系曲线，见图4(b)。由图4(b)可见，动应力幅值对累积应变变化有显著影响，动应力幅值超过100 kPa后，累积应变在本加载周期内还存在进一步扩展趋势，表明湿化作用对铁路扩能改造有显著影响。

图4 累计应变与循环加载次数的关系曲线

1.5.2 滞回曲线变化特征

120 kPa动应力幅值下不同循环加载次数的滞回曲线见图5。随着振动次数的增加，滞回圈出现明显右移，在前10 000次内滞回圈平移距离较大，随后平移距离逐渐减小并趋于稳定，表明产生累积变形，且累积变形先增大后逐渐稳定。将不同循环加载次数下的滞回圈平移至原点可以更加直观地看出滞回圈逐渐倾斜，斜率降低，说明发生了应变软化。

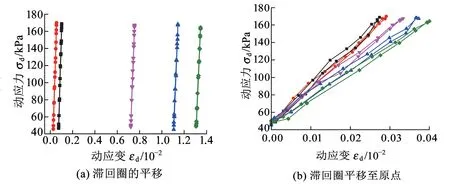
图5 120 kPa动应力幅值下不同循环加载次数的滞回曲线

1.5.3 累积变形随动应力幅值变化规律

在相同循环加载次数下，累积变形随动应力幅值的增加而增加，在循环加载次数较低时动应力幅值对累积变形影响较小，浸水后前10 000次过程内累积变形增加最多，随后增加量减小，见图6。

图6 累积应变与动应力幅值的关系曲线

1.5.4 动应力幅值对浸水速率的影响

浸水装置为常水头马氏瓶，保持水头高于试样，在振动达到1 000次时开启浸水阀门，动力湿化过程随即开始。整个动力湿化过程中不同动应力幅值下浸水量与时间的关系曲线见图7，在相同动应力幅值下，浸水量在开始阶段较大随后逐渐变小，分析其原因是由于试样非饱和，开始阶段土体中基质吸力较大，在基质吸力作用下吸水较快，随着浸水量的增加，土样基质吸力降低；另外，在动应力作用下，土体被压实、孔隙率减小，渗透性降低。浸水速率随动应力幅值的增加而减小，由于动应力越大越容易将土体压密实，因此动应力幅值越大浸水速率越低、浸水量越小。

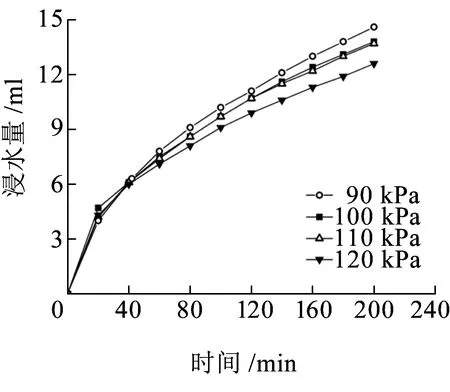
图7 不同动应力幅值下的浸水量-时间关系曲线

2 动力湿化模型的建立

2.1 修正的Iwan串联模型

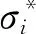
(2)

式中：l0为纯弹性元件的长度；l为弹塑性元件的总长度；N为元件总数；ε为总应变；Ei为第i个元件刚度；εi为第i个元件应变。

Iwan模型详细描述可参见文献[23]。蔡袁强[23]在Iwan串联模型的基础上添加了考虑软化的应变软化模型并串联了一个理想刚塑性元件反应累积塑性应变，得出了修正的Iwan模型。利用该模型可以同时实现滞回圈的平移与倾斜，很好地分析了软黏土应力应变关系，其应变表达式为

(3)

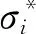
2.2 动力湿化模型

本文以修正Iwan模型为依据，以动力湿化试验为依托，提出动力湿化条件下的软化模型和动力湿化条件下的累积塑性应变模型。

2.2.1 动力湿化条件下软化模型的建立

目前，对于循环荷载作用下应变软化的研究还不够深入，无法从理论上建立应变软化模型，只能通过试验结果进行拟合，大多数研究者是通过建立软化指数与循环加载次数的关系进行拟合[23-24]。本文依据此方法，将动力湿化试验数据进行拟合，得出了软化指数与循环加载次数的关系为

δw=A-BlnN

(4)

式中：δw为湿化条件下的软化指数；N为循环加载次数；A、B是与土样类型、性质及应力水平有关的试验常数。

动力湿化条件下，各动应力幅值对应的软化模型拟合曲线见图8。

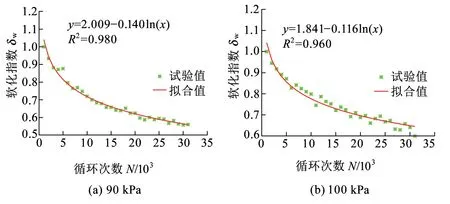
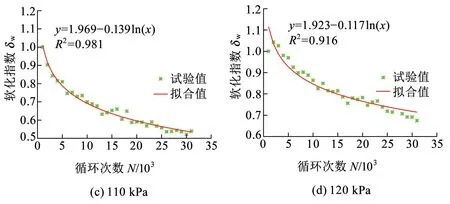
图8 不同动应力幅值下应变软化模型拟合曲线

2.2.2 动力湿化条件下累积塑性应变模型的建立

累积塑性应变的预测模型较多，通常的思路是建立累积塑性应变与循环加载次数之间的关系。其中，指数模型最为常用[23]，其式为

εp=CNd

(5)

式中：C、d为与土样类型、性质及应力水平有关的试验常数。

本文将动力湿化过程的累积变形与循环加载次数关系曲线进行拟合，得出动力湿化条件下的累积塑性应变模型为双曲线模型，即

(6)

式中：εpw为湿化条件下的塑性应变；a、b是与土样类型、性质及应力水平有关的试验常数。

动力湿化条件下，各动应力幅值对应的累积塑性应变模型见图9。

将动力湿化条件下的软化模型和累积塑性应变模型代入到修正Iwan模型中，建立动力湿化模型为

(7)

式中：εw为湿化条件下的总应变。

图9 不同动应力幅值下累积塑性应变模型拟合曲线

3 模型验证

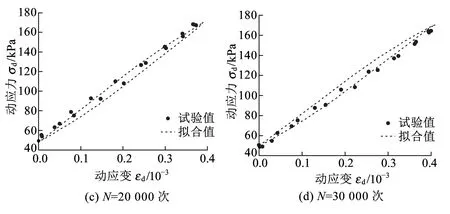
图10 不同循环加载次数下模型值与试验值比较

为验证模型的合理性，本文利用动力湿化模型，编写计算程序，将从塑黄铁路原平工务段得到的试验值与模型计算值进行对比。土样参数见表3，图10为其在120 kPa动应力幅值下的模型值与试验值的拟合关系曲线。为观测方便，不考虑累积应变变化，将图10原点平移，结果见图11。由图11可见，本文提出的模型能够很好地反映土体在动力湿化条件下的应力-应变关系。

表3 土样参数

图11 不同循环加载次数滞回圈斜率的试验值和拟合值对比关系

4 结论

本文通过对现场病害路段的基床土进行不同动应力幅值下的动力湿化试验，分析了湿化变形与循环加载次数的关系以及滞回圈的特征，并提出动力湿化条件下的应变软化模型和累积塑性应变模型，结合修正的Iwan模型提出动力湿化模型，并验证了模型的合理性。初步结论与建议如下：

(1) 在修正Iwan模型基础上，提出了考虑湿化与循环荷载耦合作用的动力湿化模型。

(2) 滞回圈会随着振动次数的增加而出现右移，在前10 000次振动内平移距离较大，随着振动次数增加平移距离逐渐减小并趋于稳定，同时滞回圈还会随着振动次数的增加而倾倒。

(3) 利用动力湿化模型计算出的滞回圈与试验实测值有较好的吻合关系，利用该模型可以很好地预测基床在动力湿化条件下的变形特性。