不同车辆-轨道垂向动力学模型功率流传递特性研究
徐 宁,任尊松,薛 蕊,李 强
(北京交通大学 机械与电子控制工程学院,北京 100044)
列车运行速度提高后,车辆对轮轨激扰的敏感性增强,轮轨激扰频率范围增大,深入研究车辆振动传递规律意义重大[1]。在车辆和轨道动力学传递特性研究中,国内外研究人员曾开展很多研究工作。Hedrick[2]以15自由度客车横向线性动力学模型为研究对象,讨论了悬挂参数的变化对临界速度和传递特性的影响;Seung等[3]以10自由度车辆垂向模型为研究对象,通过对悬挂参数的优化,提高了车辆乘坐舒适性;刘伟[4]从理论和正线测试两方面对高架线常用轨道结构垂向振动传递特性进行对比分析,探讨了参数和载荷作用位置不同引起的传递特征的变化。这些研究均给出车辆系统和轨道系统传递特征的一些结论,但未考虑车辆和轨道系统耦合作用对传递特性的影响。
翟婉明[5]建立了车辆-轨道垂向耦合动力学模型,并与传统10自由度车辆垂向模型的轮轨力、轨道加速度等时域响应结果进行了对比;翟婉明[6]为简化动力学计算,提出了22自由度轨下集总参数的车辆-轨道垂向耦合系统模型。陈果等[7]基于车辆-轨道垂向耦合模型,采用数值积为分的算法获得系统各部件垂向振动的响应,进而通过FFT变换方法求得频域传递规律,并与10自由度车辆模型的频域响应特性进行了比较;王开云等[8]基于传统车辆横向动力学模型和车辆垂、横动力学统一模型,对临界速度、轮轨横向作用力以及横向运动稳定性等性能进行了较为详细地分析比较。黄彩虹等[9]、宫岛等[10]分别采用模态叠加法和格林函数法求解了车体的振动响应问题。这些研究工作都直接和间接地分析了模型的精细化和弹性化车辆系统时、频域响应特点,但大多数没有涉及部件间的频域振动传递规律。
振动传递是部件或子结构间能量的传递,其特性的优劣主要取决于相邻部件或子结构间输入(出)能量的大小。功率流从能量角度描述振动问题,兼顾了结构上部件间的动态力和动态响应频域特征,并包含二者的相位关系,因而更为适合对大型系统振动特征进行评价。许多研究人员通过功率流描述了浮筏隔枕系统[11]、轨道结构[12]的振动传递特征,对于复杂系统悬挂参数的混合控制[13]研究方面,功率流也成为能否有效抑制系统振动传递的重要评价指标。鉴于此,本文基于4种精细化程度不同的车辆-轨道动力学模型,利用解析方法建立了形式统一的系统部件间功率流传递特征,给出了车辆一系悬挂、二系悬挂、轮轨与钢轨间以及钢轨和轨枕间的振动功率流传递规律,比较不同模型下各部件间功率流传递特征的差异,讨论悬挂参数的变化对部件间功率流传递特征的影响。
1 车辆-轨道垂向系统动力学模型及其统一形式的数学表达
1.1 几种垂向模型及其自由度描述
常见的车辆-轨道系统垂向动力学模型有:10自由度车辆垂向动力学模型[5];22自由度车辆-轨道垂向耦合动力学简化模型[6];车辆-轨道垂向耦合动力学模型[7];考虑车体弯曲振动的车辆-轨道垂向耦合动力学模型[8]。图1~图4为这4种动力学模型示意图。
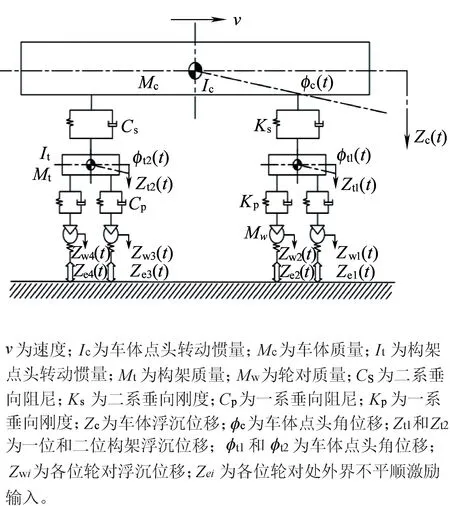
图1 10自由度车辆垂向动力学模型(模型Ⅰ)
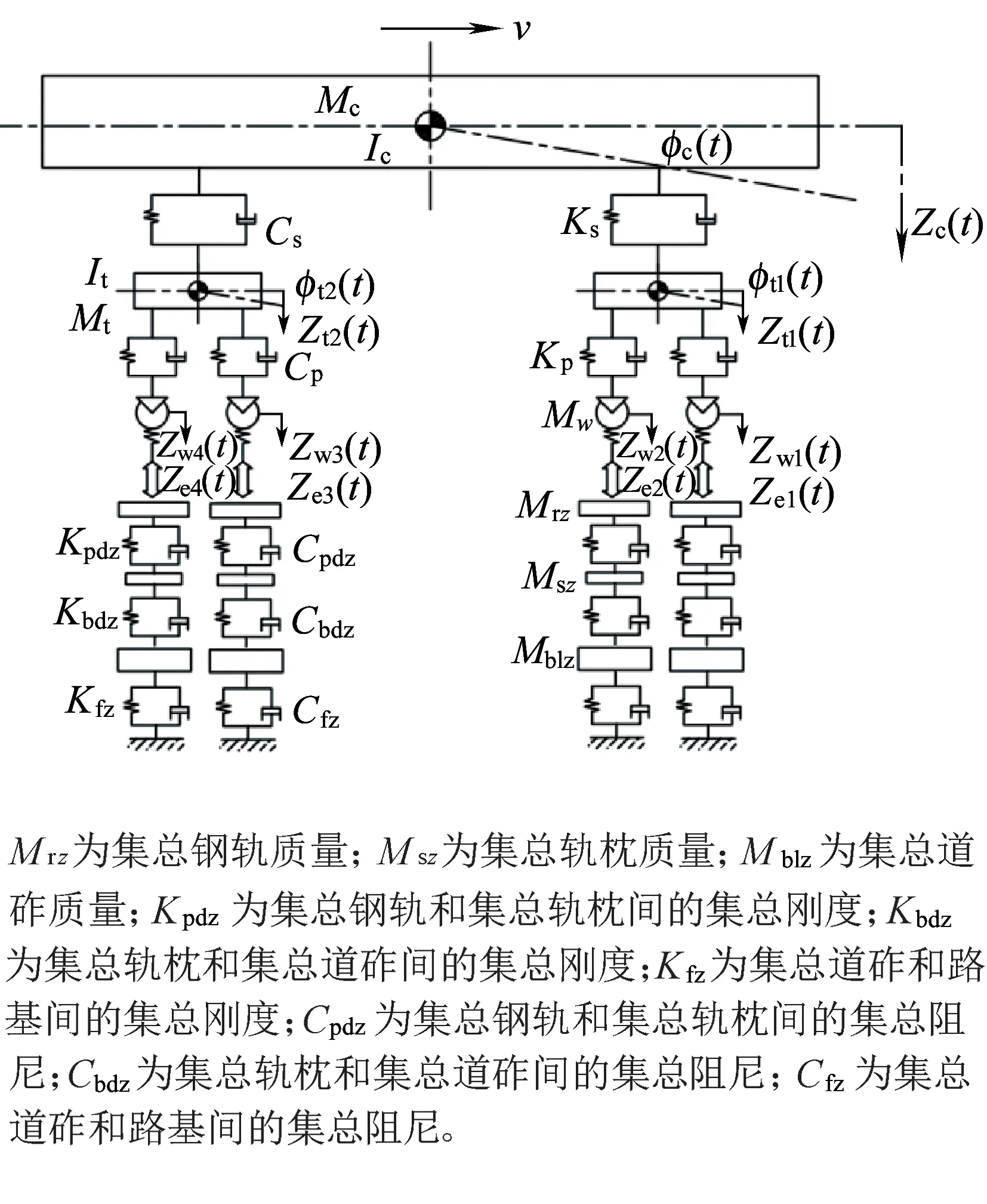
图2 22自由度车辆-轨道垂向集总参数动力学模型(模型Ⅱ)
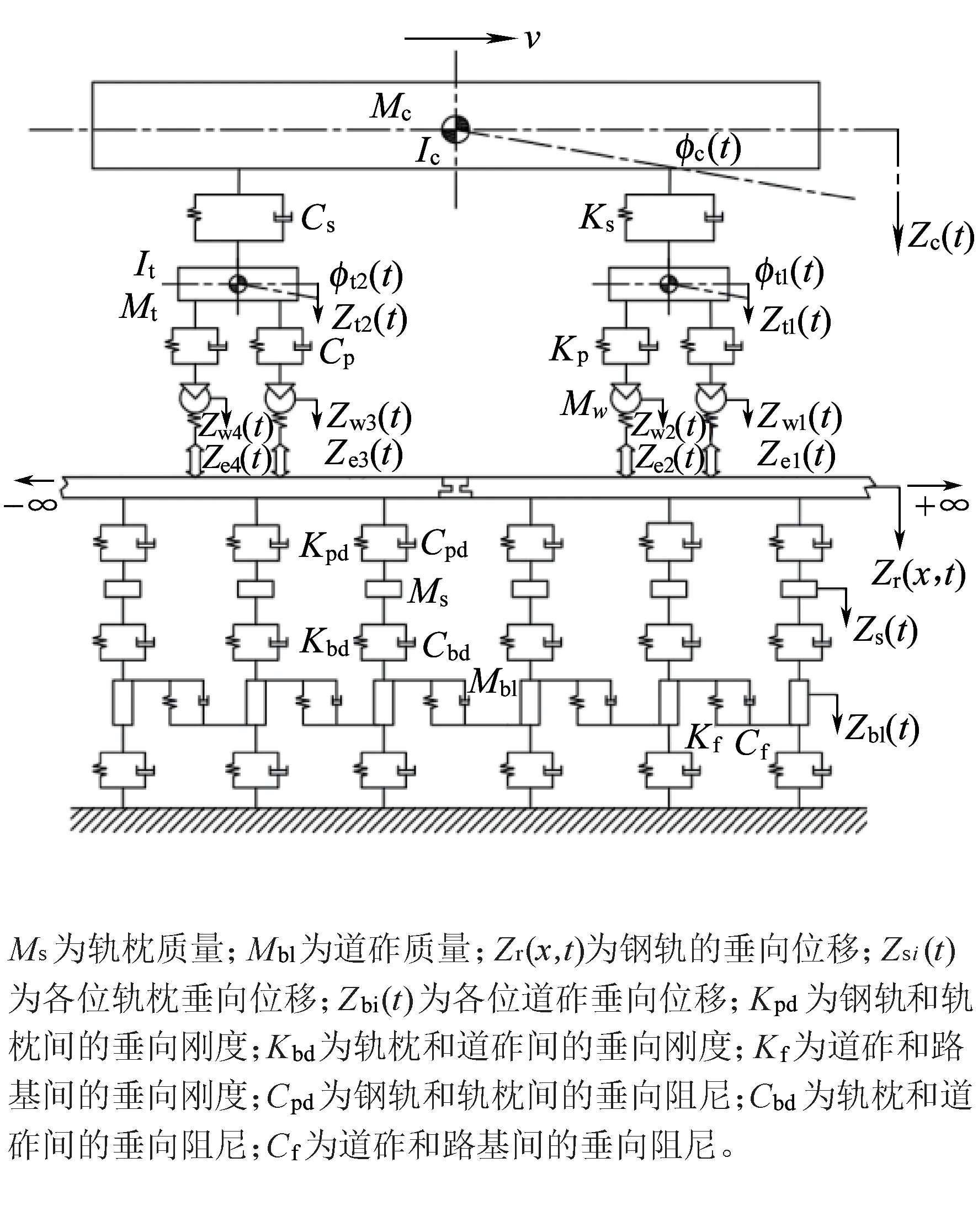
图3 车辆-有砟轨道垂向耦合动力学模型(模型Ⅲ)
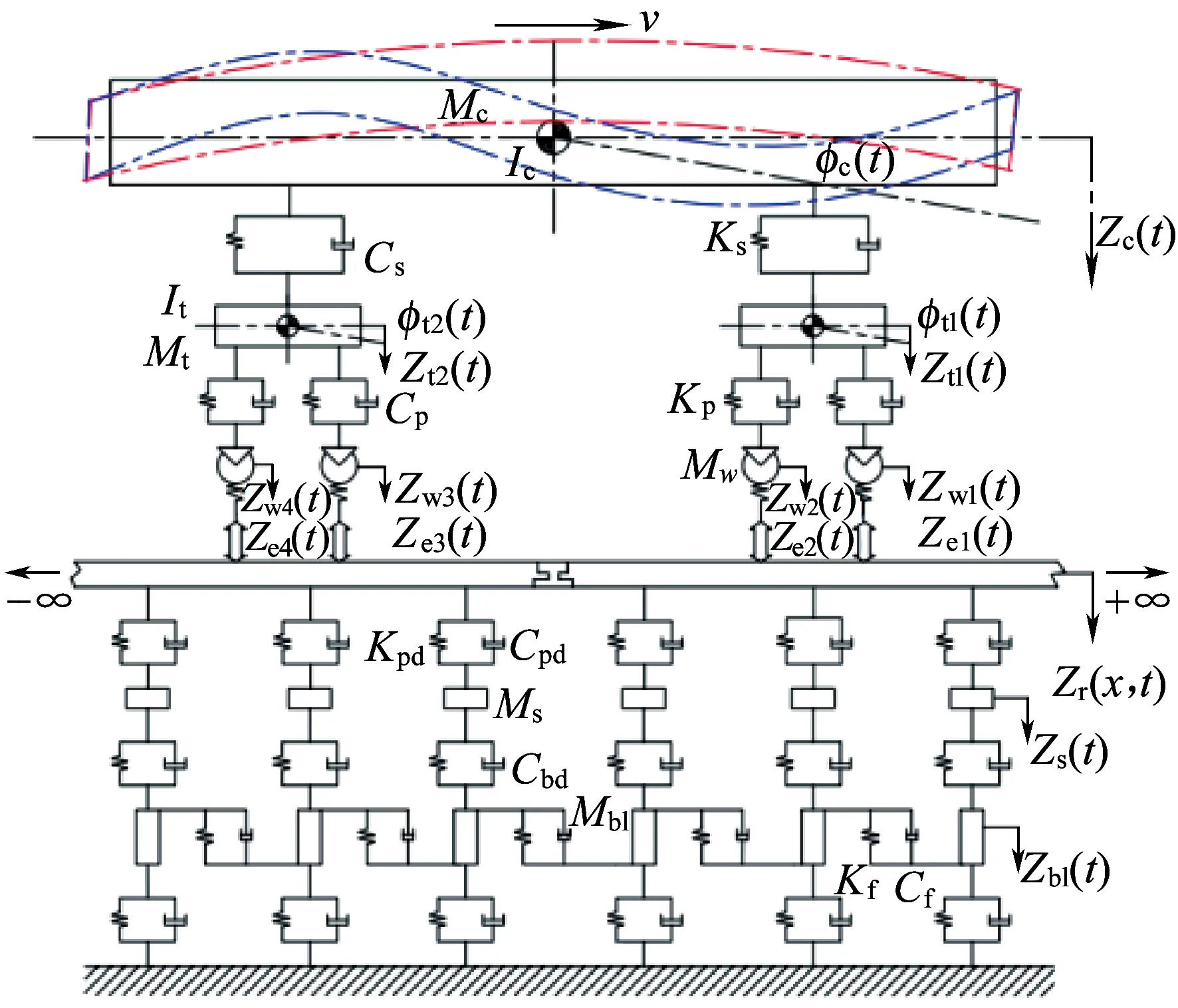
图4 考虑车体弯曲振动的垂向耦合动力学模型(模型Ⅳ)
比较图1~图3可以看出,这3种模型中包含的车辆各部件自由度完全相同,仅是钢轨及其以下的部分有所区别。共有的自由度包括:车体及一位和二位构架的浮沉和点头运动;一到四位轮对的浮沉运动。10自由度车辆垂向动力学模型将轨下视为绝对刚性,不考虑轨下各部件的惯性以及支撑刚度和阻尼;22自由度车辆-轨道垂向耦合动力学简化模型的轨下部分包含1~4位轮对位置处集总钢轨、集总轨枕以及集总道床的浮沉自由度;车辆-轨道垂向耦合动力学模型中轨下部分包括钢轨的MN阶简支模态,N个支撑轨枕和N个道砟的浮沉自由度。
由图3、图4可以看出,考虑车体弯曲振动的垂向模型仅是比车辆-轨道垂向耦合动力学模型多包含MQ阶车体弹性梁弯曲振动,二者的其他自由度完全相同。为叙述方便,在后续文中图1~图4中模型分别记为模型Ⅰ、模型Ⅱ、模型Ⅲ、模型Ⅳ。
1.2 统一形式的模型数学表达
模型Ⅰ~模型Ⅳ均为线性系统,都可以写作以下统一表达形式

(1)
式中:M为系统的质量矩阵;C为系统的阻尼矩阵;K为系统的刚度矩阵;z为广义自由度列向量;G为输入刚度矩阵;P为外界输入位移列向量。
式(1)中,各矩阵具体表达式为
(2)
(3)
(4)
(5)
(6)
P={ze1,ze2,ze3,ze4}
(7)
式(2)~式(6)中,下标含有Lv的各分块矩阵与车辆部分相对应,下标含有Mv的各分块矩阵与钢轨相对应,下标含有Nv的各分块矩阵与轨下部分相对应,对于模型Ⅰ~模型Ⅳ,以上分块矩阵在维数和内容上均有所差异。式(7)中ze1~ze4为1到4位轮对处外界输入位移激励。
模型Ⅳ形式最为复杂,且与实际最为接近,这里仅给出模型Ⅳ各矩阵表达式,模型Ⅰ~模型Ⅲ可参考文献[7-9]中微分方程化简得到。
对于模型Ⅳ,式(2)中M的分块矩阵M1表达式为
(8)
其中,M1_1~M1_4表达式为
M1_1=IMQ×MQ
(9)
(10)
M1_4=diag
[Mc,Ic,Mt,It,Mt,It,Mw,Mw,Mw,Mw]
(11)
式(9)中,I*×*代表*行*列的单位矩阵,式(10)中mzi和mθi(i=1~MQ)的表达式为

(12)
(13)
式(2)中M的分块矩阵M2、M3为
M2=IMN×MN
(14)
(15)
M3_1=MsIN×N
(16)
M3_2=MblIN×N
(17)
式(16)、式(17)中:Ms和Mbl分别为轨枕和集总道砟的质量。
式(3)中分块矩阵K1~K7的表达式为
(18)
(19)
(20)
(21)
(22)
其中
K1_1=
(23)
(24)
K5_1=-KpdYp
(25)
K7_1=(Kpd+Kbd)IN×N
(26)
K7_3=K7_2=-KpdIN×N
(27)
(28)
式(23)中,Y1和Y2表达式为
Y1=[Yc1(xc1),Yc2(xc1),…,YcMQ(xc1)]T
(29)
Y2=[Yc1(xc2),Yc2(xc2),…,YcMQ(xc2)]T
(30)
式中:Yci(x)为车体各阶梁函数;xc1和xc2为一、二位构架与车体二系悬挂处沿长度方向的坐标;Kr、Yw和Yp为与钢轨模态相关的矩阵。
[Kr]MN×MN=diag[Kr1,Kr2,…,KrMN]
(31)
式中:diag[·]为对角矩阵;Kri具体表达为
(32)
[Yp]MN×N=
(33)
[Yw]MN×4=
(34)
Yi的具体表达式为
(35)
式(32)和式(35)中:Mr为单位长度钢轨质量;lr为钢轨长度;EI为钢轨抗弯刚度。
式(4)中分块矩阵C1~C5的表达式分别见式(36)~式(39)。式中各子块矩阵的表达式为式(40)~式(45)。
(36)
C2=Cpd[Yp][Yp]T
(37)
(38)
(39)
(40)
(41)
C3_1=-CpdYp
(42)
C5_1=(Cpd+Cbd)IN×N
(43)
C5_3=C5_2=-CpdIN×N
(44)
(45)
式(5)中,分块矩阵x2和x3的表达形式为
x2=[qr1,qr2,…,qrMN]T
(46)
x3=[zs1,…,zsN,zbl1,…,zblN]
(47)
式中:qri(i=1~MN)为钢轨各阶模态物理坐标。
输入刚度矩阵式(6)中分块矩阵G1和G2可见式(47)、式(48)。
G1=KhI4×4
(48)
G2=-KhYw
(49)
2 部件间功率流传递函数的建立
对式(1)进行傅里叶变换,可得
(K+iωC-ω2M)X(ω)=GP(ω)
(50)
由式(49)经过化简可以得到各部件输出位移和速度频域列向量,得
X(ω)=H(ω)P(ω)4×1
(51)
V(ω)=iωH(ω)P(ω)4×1
(52)
式中:H(ω)为位移传递函数,其表示为
H(ω)=[(K+iωC-
ω2M)-1G](Lv+Mv+Nv)×4
(53)
式(51)、式(52)中,X(ω)和V(ω)中各行元素分别与系统中各自由度对应位移和速度频域响应,进而可求出一位构架和一位轮对间一系悬挂力Fp为
Fp(ω)=Kp(X(Lv-3)-(X(Lv-6)lb+
X(Lv-7)))+Cp(V(Lv-4)-
(V(Lv-6)lb+V(Lv-7)))
(54)
车体和一位构架间二系力Fs为
Fs(ω)=Ks(X(Lv-6)lb+X(Lv-7)-
Cs(V(Lv-6)lb+V(Lv-7)-
(55)
依照上述方法可获得一位轮对处轮轨力Fwr、钢轨与(附近)支撑轨枕间垂向力Fpd、附近撑轨枕与道砟间垂向力Fbd
(56)
式中:adj(·)代表与·最接近的支撑轨枕对应的钢轨坐标。
依据式(56)的功率流计算公式,可获得车辆-轨道垂向系统各相邻部件间的功率流
(57)
将线性系统位移和速度之间的关系带入式(57)中,可以得到关于部件位移的功率流计算式
(58)

以上4种模型具有空间对称性,根据文献[12],从轨道不平顺到车辆各部件的幅频传递特性可转化为从任一位轮对到该部件的幅频传递函数与“间距函数”的乘积。由式(51)、式(52)得到响应函数,仅考虑由一位轮对处激励产生的部分即可。以计算Fp(ω)为例,其结果见式(58),进而求出传递功率流Pp(ω)。
Fp(ω)=Kp{H(Lv-3,1)-
[H(Lv-6,1)lb+H(Lv-7,1)]}+
iωCp{H(Lv-4,1)-
[H(Lv-6,1)lb+H(Lv-7,1)]}ze1(ω)
(59)
Pp(ω)=Kp{H(Lv-3,1)-
[H(Lv-6,1)lb+H(Lv-7,1)]}+
iωCp(H(Lv-4,1)-
[H(Lv-6,1)lb+H(Lv-7,1)]·
iω[H(Lv-6,1)lb+H(Lv-7,1)]·
(60)
3 计算结果及分析
为便于对比分析,按照文献[14]的方法求得模型Ⅰ~模型Ⅳ在标准参数下系统固有频率和模态特征向量。具体结果见表1。

表1 几种动力学模型下系统固有频率和振型
注:①为不计道砟间的相互作用,即Kwd和Cwd为零的情形;②为考虑道砟间的相互作用的情形。
3.1 车辆-轨道垂向耦合系统部件间功率流传递特性
模型Ⅲ是理论分析和数值计算中较为常用的模型,首先给出模型Ⅲ在标准悬挂参数下的功率流传递特性。轨上和轨下部分部件间功率流传递特性见图5、图6。图5、图6中传递函数符号的数值大小本身并没有意义(以下各图同),仅代表功率流的流向以及系统的吸振和减振特性,传递函数符号为正时,代表该频段的能量能够较为顺利流入该部件,传递函数符号为负时,代表该频段能量由路径流出部件或流入部件的能量得到衰减[16],本文中功率流符号为负可看作流入部件的能量获得衰减和较为有效的抑制。
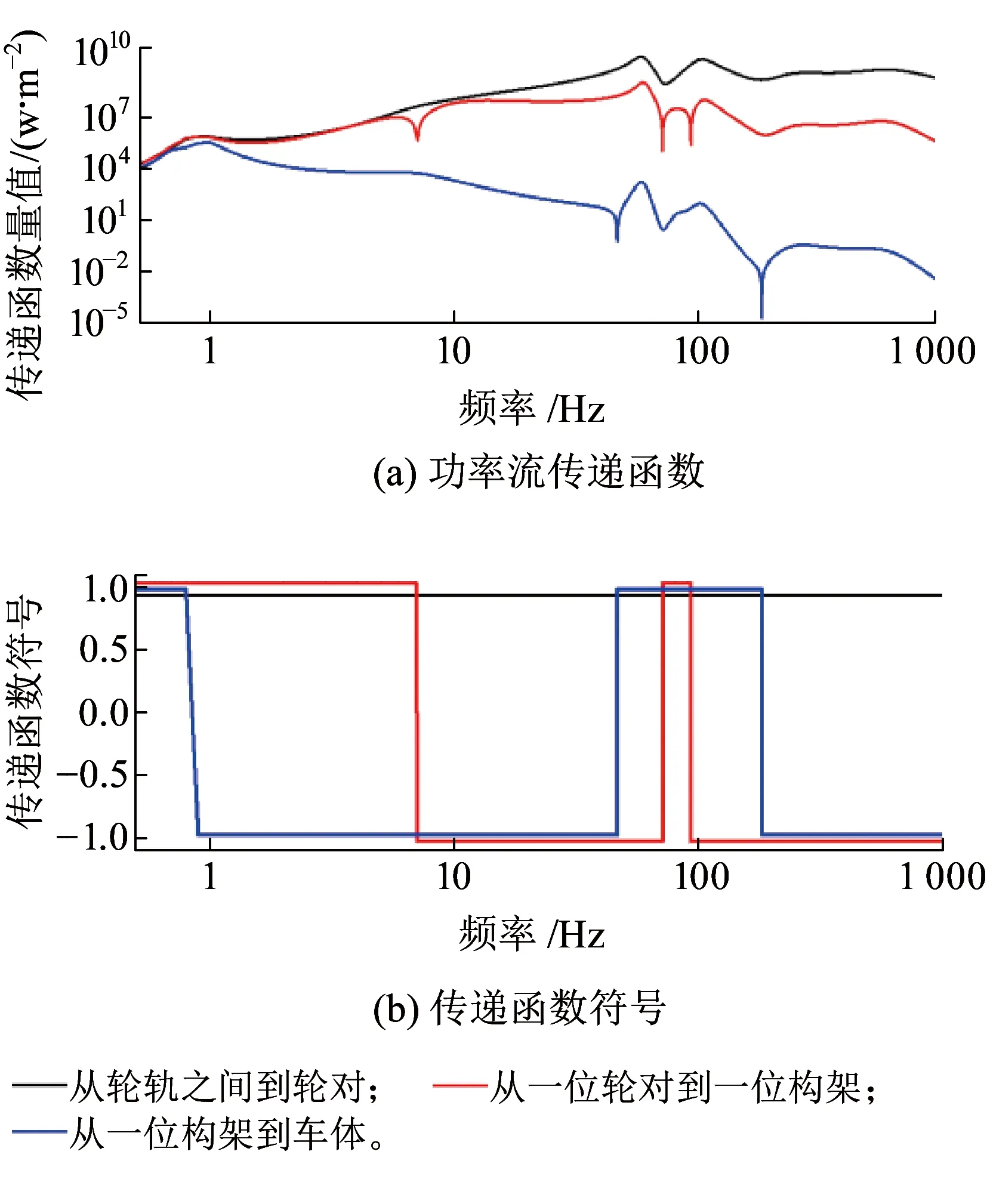
图5 轨上部分部件间功率流传递函数
由图5(b)、图6(b)可以看出,由轮轨激励能量至轮对和道砟的传递功率覆盖0~1 000 Hz的全频带。构架仅在小于7 Hz频段上以及70~95 Hz间实现了激励能量传递。
至车体的传递能量包含0~0.8 Hz以及45~185 Hz 两个频段。传递至钢轨的能量包含除1~2 Hz以外的全频带,至轨枕的传递能量为频率10~500 Hz间的频带,至道砟的能量为0~130 Hz的频带。说明系统的刚度和阻尼参数的配置能够使得从激励源到达上层车辆部件的能量流主要为一个或几个低频区段,而流向轨下部件的能量则主要为频率较高的频段。
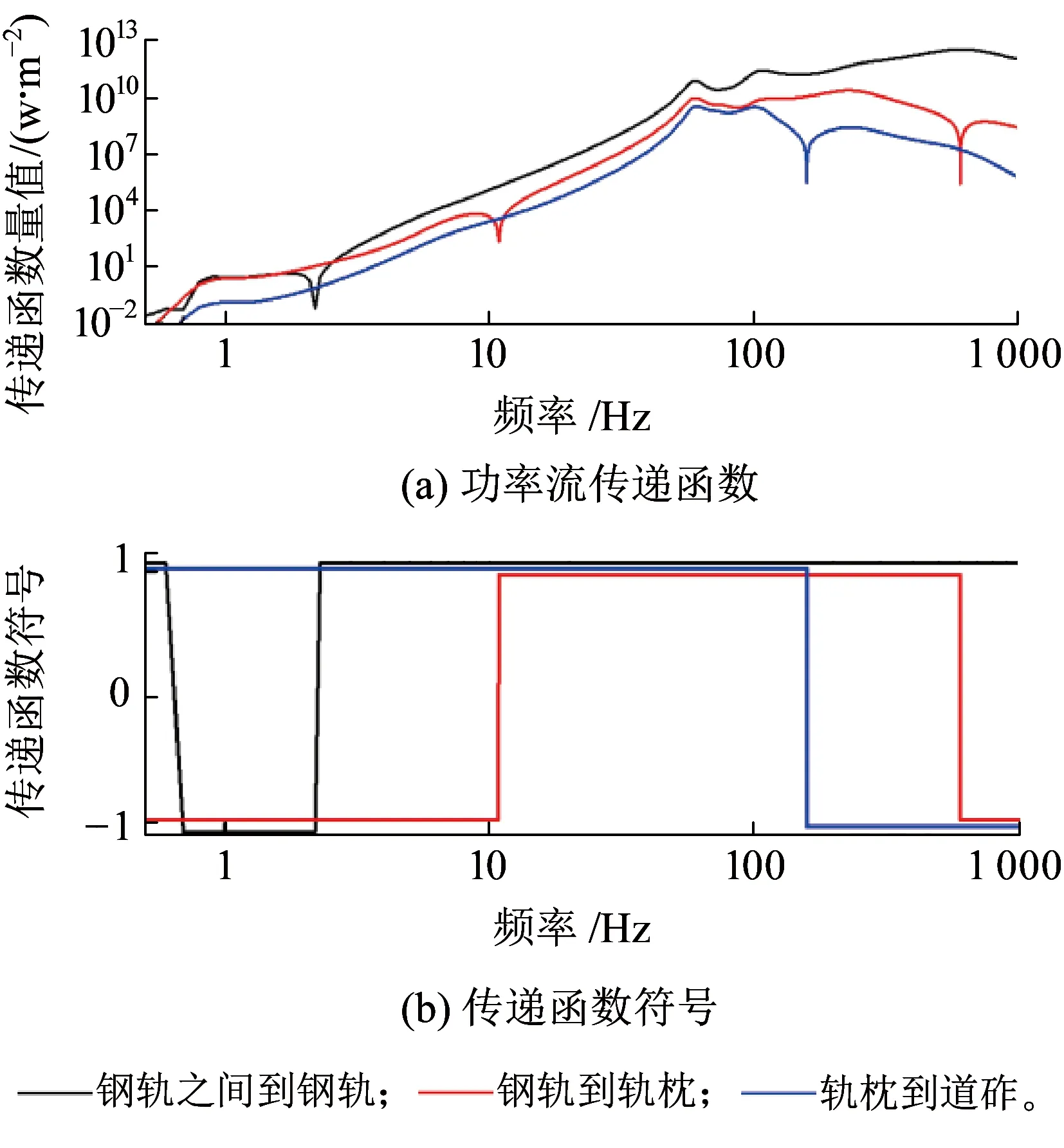
图6 轨下部分部件间功率流传递函数
由图5(a)、图6(a)可以看出,构架到车体的传递函数在小于1 Hz范围相对较大,在45~185 Hz这一频段较小;轮对到构架传递函数在小于7 Hz和70~95 Hz 两个频段数值相近。由轮轨间到轮对的传递函数在大于30 Hz的频段上能保持在一定数量级以上,且在50~60 Hz以及95~125 Hz 两个频段能够具有相对较大数值的传递函数。至轨下各部件传递函数在50~125 Hz均具有较大数值。结合表1可以发现,55~60 Hz和70~120 Hz这两个频段分别与轮对浮沉振型及轨下部件耦合振型相对应。说明位于激励源附近位置的轮对和钢轨,其固有频率附近的激励能量往往具有较强的传播性,致使车体、道砟这样位于路径终端的部件在这些频段上依旧具有较大量值的传递函数。此外,在部件各自的固有频率区,该部件往往具有传递函数的最大值,如在频段0.7~0.9 Hz上构架到车体的传递函数,在频段500~700 Hz上轮轨间至钢轨的传递函数以及在频段200~220 Hz上钢轨到轨枕的传递函数。
3.2 不同模型对功率流传递特性的影响
从形式上,模型Ⅰ~模型Ⅳ中包含的自由度逐渐增多,精细化程度逐渐增强,不可避免地引起部件间功率流传递主频及各传递主频上传递率发生改变。图7~图11中给出了不同模型下部件间功率流传递函数的比较。在轨下部件动力学研究中也常有不考虑道砟间相互作用的情况,因而在对比轨下部件间功率流传递时,这一情况也包含在内。
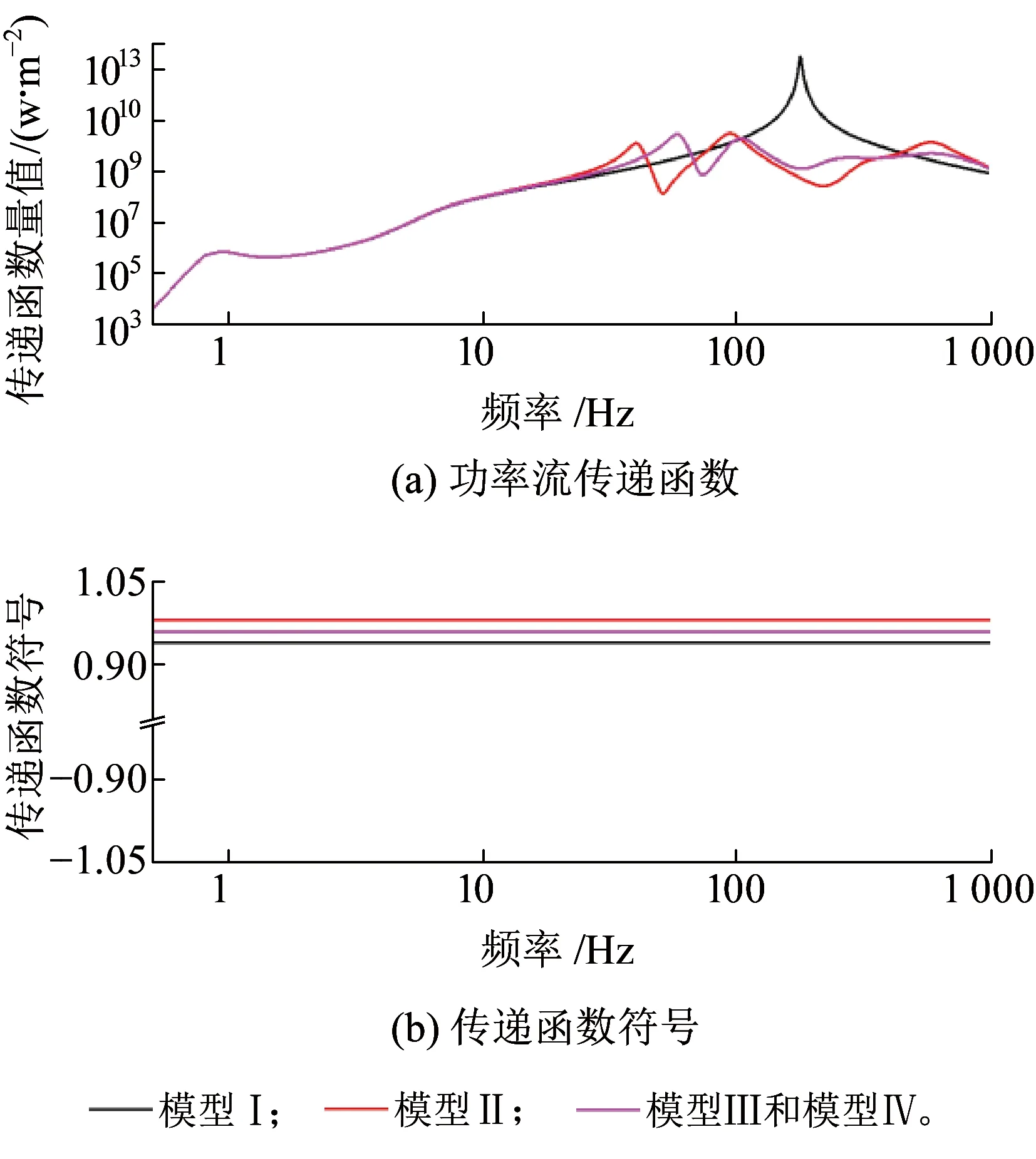
图7 不同模型-轮轨间到轮对功率流传递函数对比
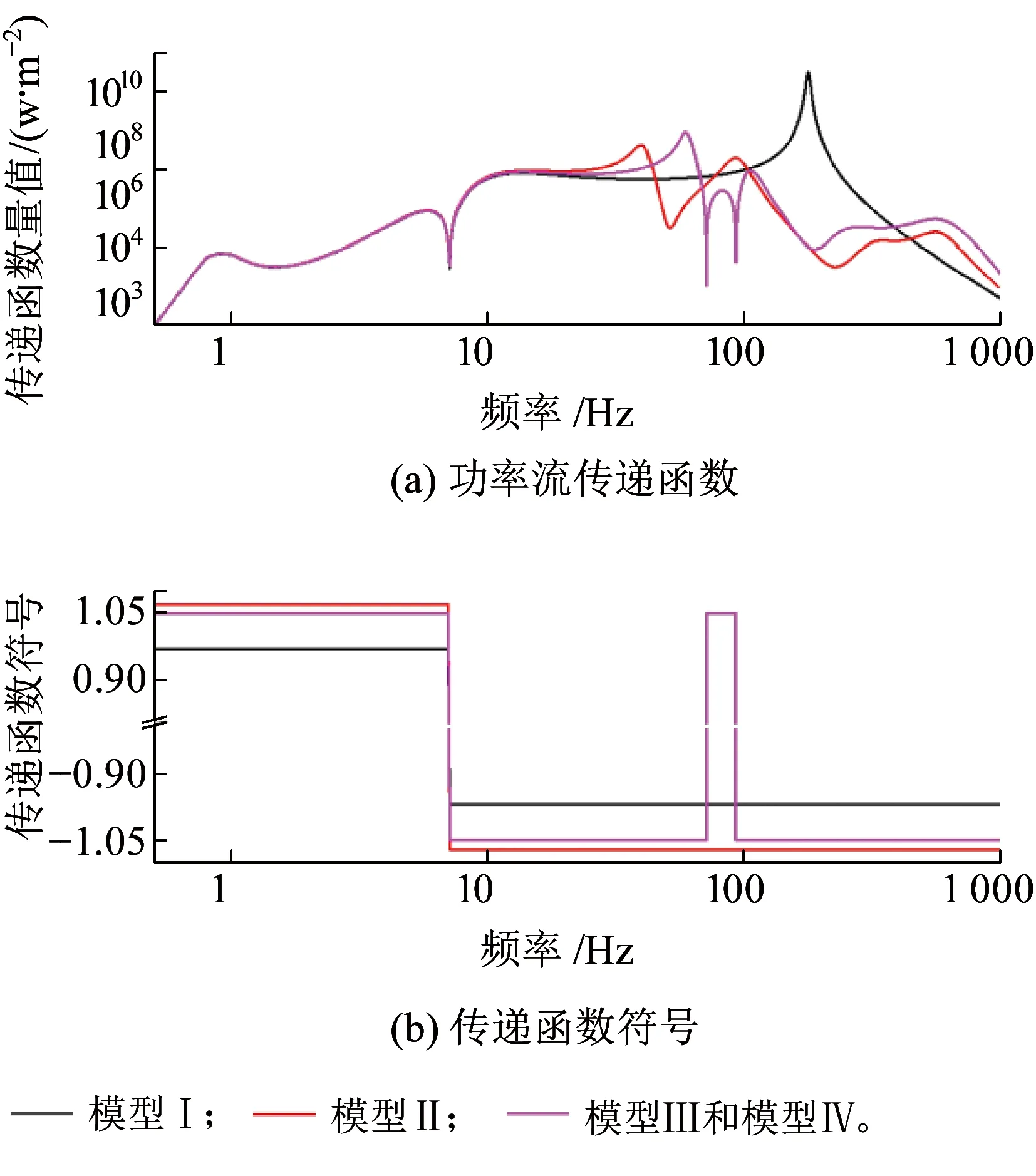
图8 不同模型一系悬挂功率流传递函数对比
由图7~图9可以看出,4种模型中,至轮对和构架的传递函数在10 Hz以下基本是一致的,至车体的传递函数在5 Hz以下也是一致的,说明简单模型对于车辆低频传递特性的模拟式较为真实。模型Ⅰ中,传递函数在大于20 Hz的频段上仅有178 Hz轮对浮沉振动主频附近具有一量值很大的极大值,这与模型Ⅰ缺少轨下弹性支撑、整体刚度较大有关。根据传函符号,这一频段功率流并不会流向构架和车体。与模型Ⅰ相比,模型Ⅱ~Ⅳ中轨下多级支撑的引入使得系统整体刚度变小,致使轮对浮沉模态主频分别变为39~40 Hz和58~60 Hz之间,且模型Ⅱ中,至车体和构架的传递函数在大于20 Hz的频段上也几乎没有能量流入,这与真实情况的吻合程度较低。
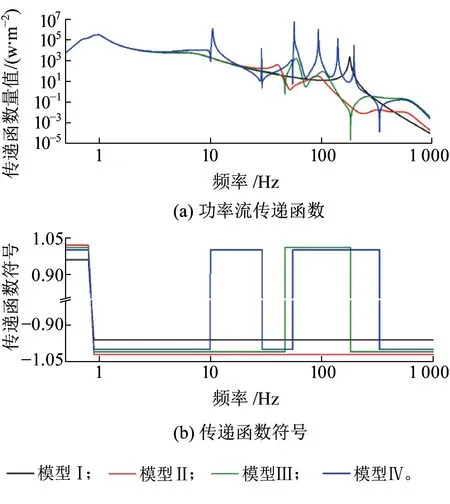
图9 不同模型二系悬挂功率流传递函数对比
模型Ⅳ中,至车体的传递函数在弯曲振动主频下均为极大值,但至构架和至轮对传递函数,模型Ⅲ和Ⅳ几乎完全相同,说明车体的弯曲振动仅对车体自身的传递特性有较为显著的影响,对相邻部件传递特性的影响极为微小。
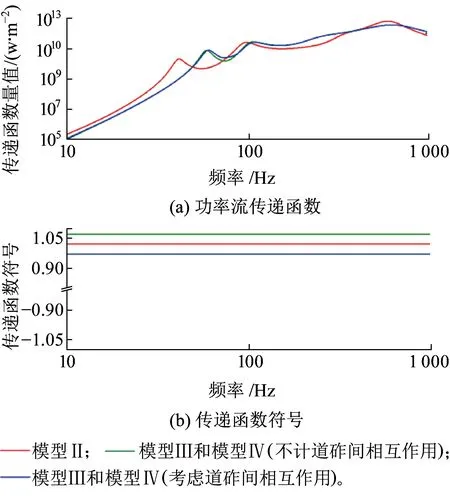
图10 不同模型轮轨间到钢轨功率流传递函数对比
由图10~图12可以看出,模型Ⅱ中,轨下部件的传函符号始终为正,说明采用轨下集总参数模型,0~1 000 Hz的频率范围内能量均能流入各部件,这与模型Ⅲ和Ⅳ中流入轨枕和道砟的能量仅为一定频率段内的情况有所不同,且在大于200 Hz的频段上,模型Ⅱ中至轨枕和道砟传递函数在数值上都大于模型Ⅲ和Ⅳ,说明集总参数模型对于轨枕和道床两部件的振动频域特征描述上准确程度有所欠缺。考虑道砟间的相互作用能够使流入轨枕的能量频率范围减小并向低频方向移动,对于道床刚好相反。在60~100 Hz频段内,不计道砟间相互作用下至各轨下部件的传递函数均小于考虑相互作用的情形,二者的差距以至道砟的传递函数最为明显。
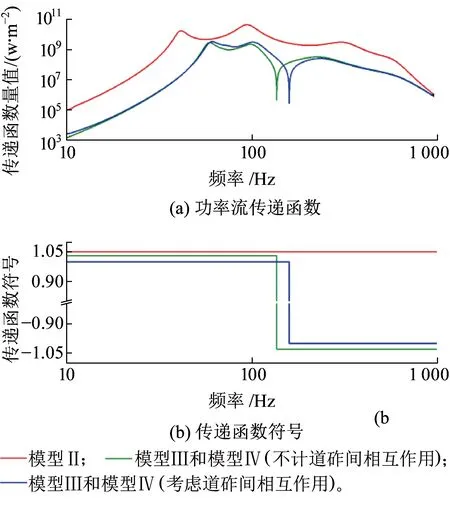
图12 不同模型轨枕-道砟间功率流传递函数对比
3.3 参数的改变对功率流传递特性的影响
由3.2节可以发现,模型Ⅳ包含系统频域特点最多,自由度的增多也使模型本身与实际更为接近。本节以模型Ⅳ为例,讨论部件质量、刚度参数以及悬挂参数的变化对于部件间功率流传递特性的影响。
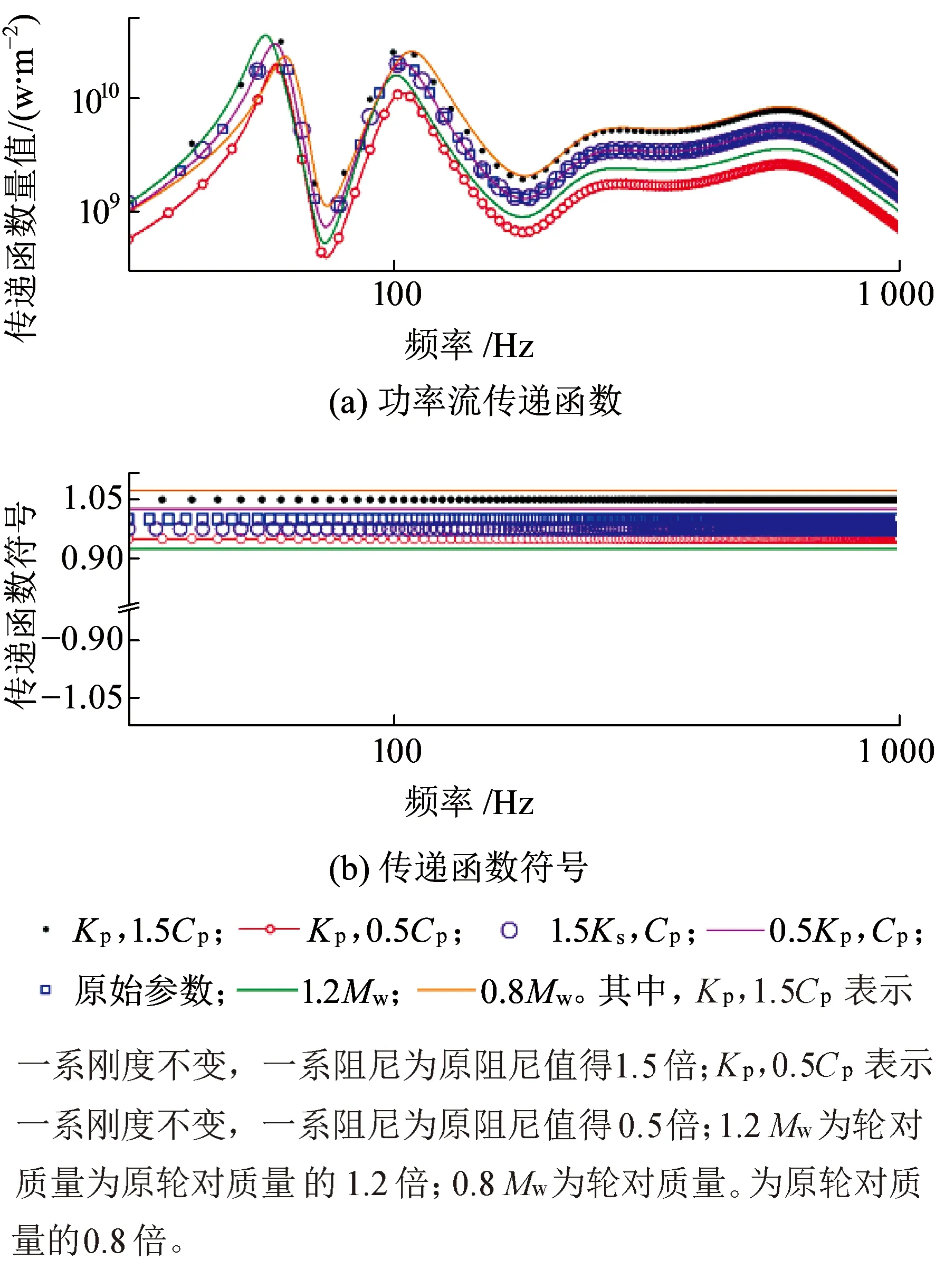
图13 一系悬挂参数和轮对质量的变化对至轮对功率流传递函数的影响
图13表征了模型Ⅳ中一系悬挂参数与轮对质量的变化对至轮对功率流传递函数的影响。由图13可以看出,对至轮对传递函数影响最大的是一系阻尼,减小一系阻尼使得在30~1 000 Hz范围内传递函数均有所减小,一系刚度的变化对传递函数的影响几乎可以忽略。轮对质量的增大,虽使得30~60 Hz范围内的传递函数增大,但使得大于100 Hz中高频传递函数有所减小。
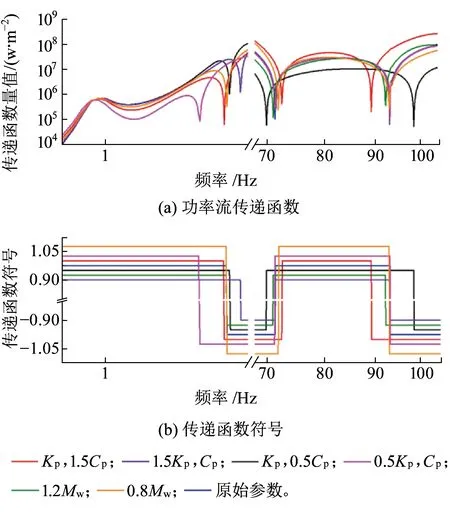
图14 一系悬挂参数和轮对质量的变化对轮对到构架功率流传递函数的影响
图14、图15表征了一系悬挂参数与轮对质量变化和二系悬挂参数与车体质量变化对轮对至构架功率流传递函数的影响。由这图14、图15可以看出,二系悬挂参数和车体质量的变化对轮对至构架传递函数影响都较小,仅影响1 Hz附近频段。一系悬挂各参数对1 Hz附近频段传递函数几乎没有影响,主要影响频段为3~7 Hz和70~90 Hz 2个频段,其中一系刚度的变化对前一频段的影响较为明显,一系阻尼的变化对于后一频段的影响较为明显。一系刚度Kp减小使7 Hz以下的传递函数明显减小,且流入构架能量的频率范围也有所减小;一系阻尼Cp减小使70~90 Hz范围内传递函数减小,但会增大流入构架能量的频率范围。此外,轮对质量的变化对轮对到构架传递函数的影响也较小。
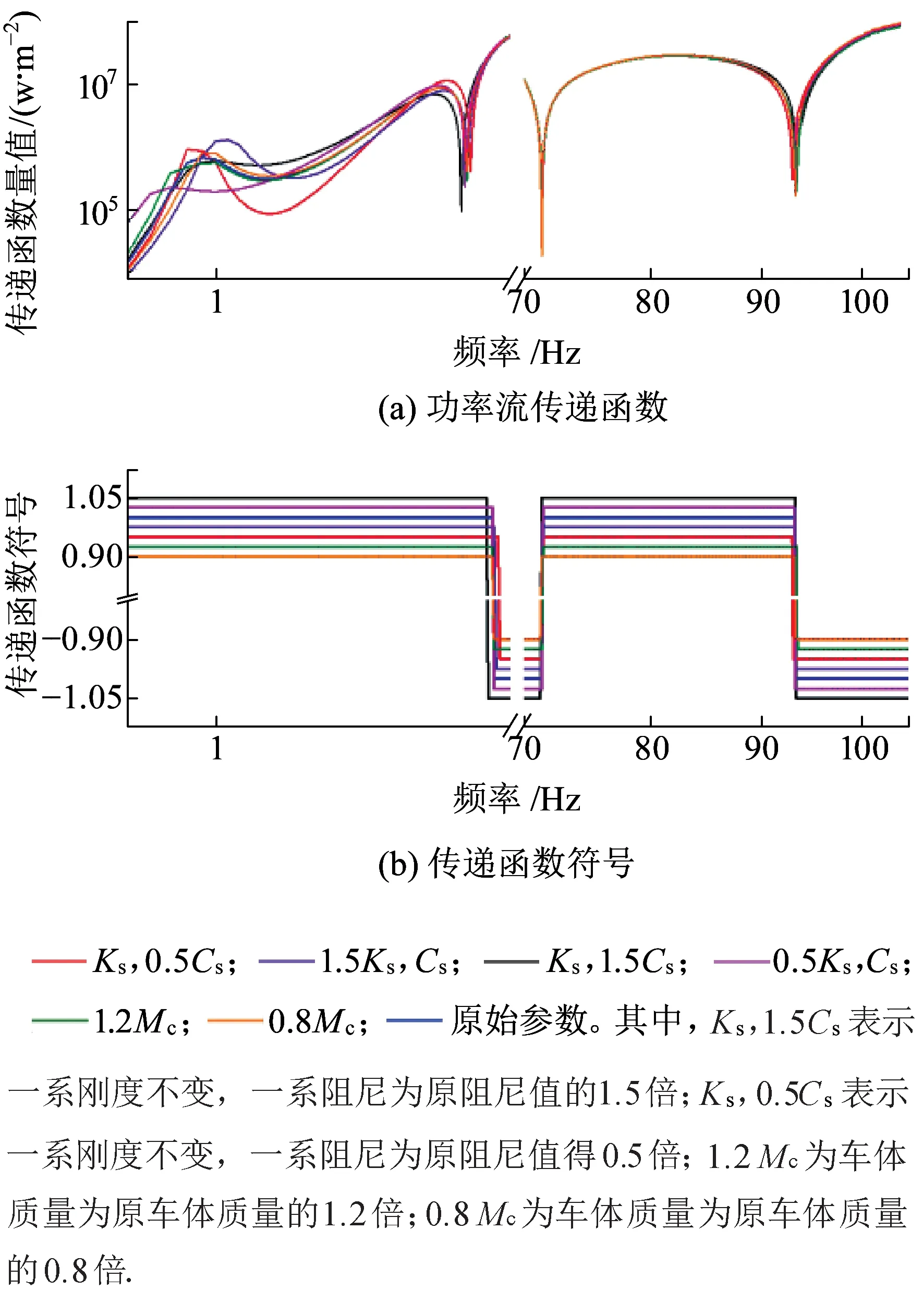
图15 二系悬挂参数和车体质量的变化对轮对到构架功率流传递函数的影响
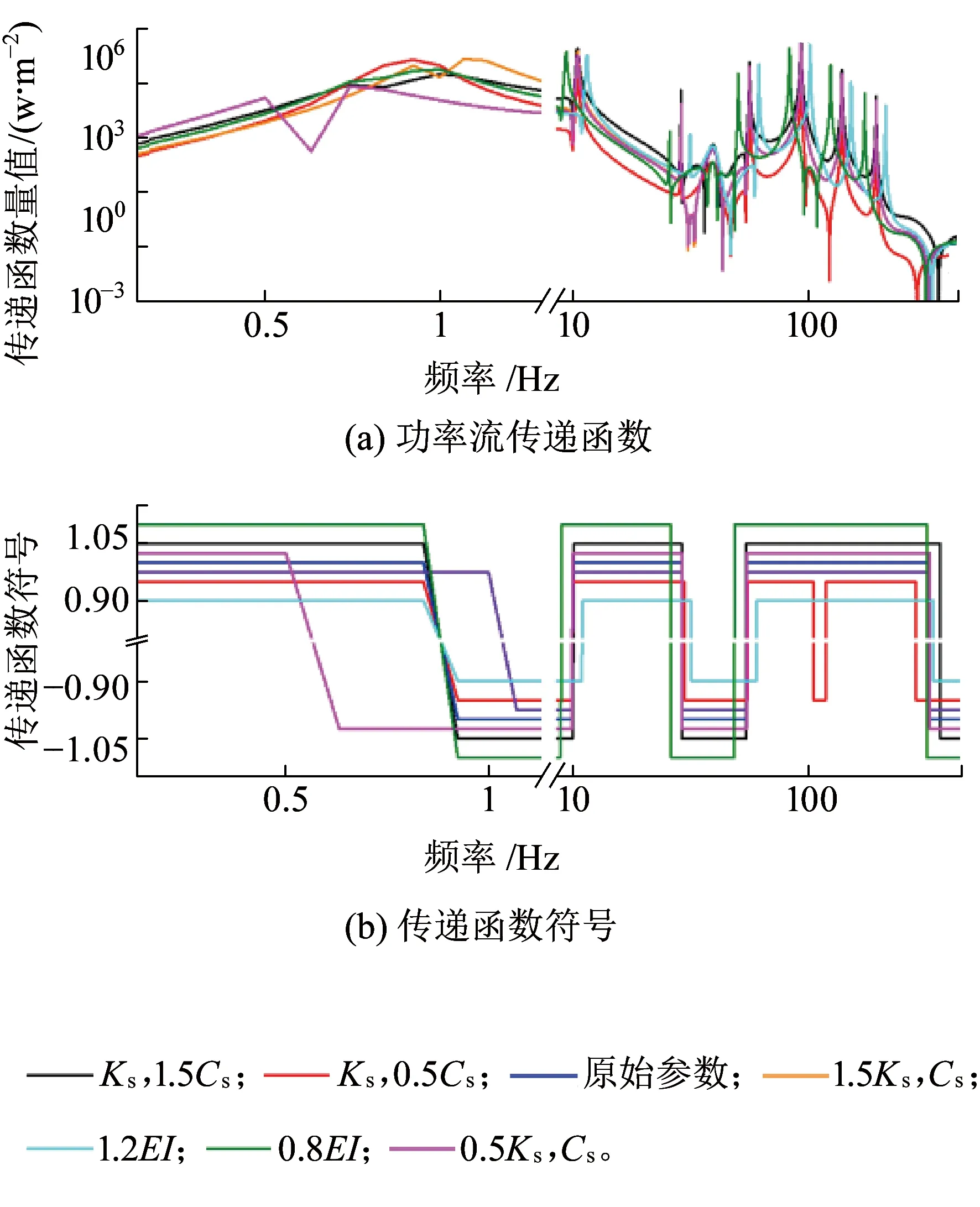
图16 二系悬挂参数和车体参数的变化对轮对到构架功率流传递函数的影响
图16显示了二系悬挂参数和车体参数的变化对轮对到构架功率流传递函数的影响。从该图可以看出,在车体弯曲振动主频附近,车体抗弯刚度EI的增大(或减小)使传递函数向较高(或较低)频率方向移动,但传递函数量值的改变并不大。二系刚度的变化对1 Hz以下低频段传递函数的影响较为明显,二系阻尼的变化对10~200 Hz较高频段传递函数的影响较为明显。二系刚度Ks减小使1 Hz附近传递函数数值明显减小,且流入构架能量的频率范围也有所减小;二系阻尼Cs减小使10~200 Hz范围内传递函数数值以及流入构架能量的频率范围都减小,但会使1 Hz附近传函数值一定程度地增大。
由图17可以看出,簧下质量对于50~100 Hz频率范围内轨下部件传递函数影响较大,对大于200 Hz的中高频传递函数影响十分微小。簧下质量的增大使50~100 Hz频段传至钢轨和道砟的传递函数值都有所增大,但对钢轨而言,500~700 Hz区间才是钢轨功率流传递的主要频段,因而簧下质量的变化对轨枕至道砟传递特性的影响最为明显。这与文献[15]中簧下质量的增大对钢轨影响较小而对道床破坏较为严重的结论相一致。
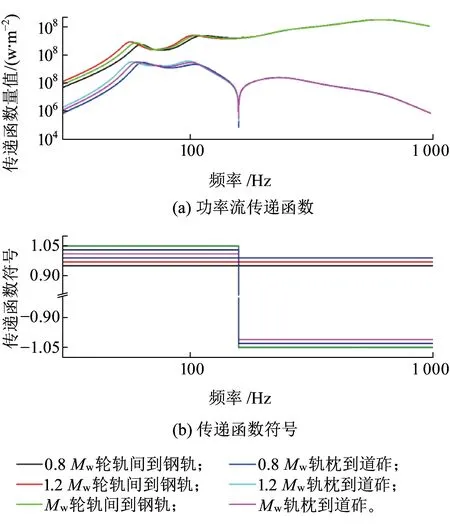
图17 簧下质量的变化对轨下部件间功率流传递函数的影响
4 结论
本文基于4种精细化程度不同的车辆-轨道垂向动力学模型,建立了相邻部件间功率流传递函数,并相应的获得以下一些结论。
(1) 从激励源传至上层车辆部件的能量主要为一个或几个低频区段,而流向到轨下部件的能量则主要在频率较高的频段。位于激励源附近位置的轮对和钢轨,在其固有频率附近(60~100 Hz)的振动能量往往具有较强的传播性,致使车体、道砟等位于路径终端的部件在这些频段上依旧具有较大量值的传递函数。
(2) 模型Ⅰ、模型Ⅱ中,对于车辆10 Hz以下低频垂向传递特性的模拟较为真实,但对中、高频传递特性的表达与复杂精细模型相差较大。且模型Ⅰ中,不能对轮轨激励作用传至轨下部件进行讨论,模型Ⅱ对于传至钢轨的振动能量模拟相对较为准确,对于传至集总轨枕和集总道床两部件振动能量模拟的准确性仍有所欠缺。
(3) 模型Ⅲ、模型Ⅳ真实和完整地反映了轨下系统,对于轨下各部件垂向频域传递特性的模拟也都较为准确。且二者对于构架和轮对的功率流传递特性的模拟也较为一致,但由于模型Ⅳ考虑了车体弯曲振动的影响,在车体弯曲固有频带附近,传至车体的功率流传递特性更为准确。
模型Ⅰ、模型Ⅱ可适用于对10 Hz以内车辆系统传递特性的描述,模型Ⅲ、模型Ⅳ适用于较高频率范围内车辆系统传递特性的描述,模型Ⅳ能够更为准确地反映车体固有频率附近的传递特征。
(4) 一系刚度的改变对轮轨间传至轮对的传递函数几乎没有影响,一系阻尼的减小使得在30~1 000 Hz范围内传递函数有所减小。对于轮对传至构架的传递函数而言,二系悬挂参数的变化仅对1 Hz附近频段的传递函数有一定影响,一系刚度变化对3~7 Hz频段传递特性有影响,一系阻尼变化对70~90 Hz传递特性有影响。在车体弯曲振动主频附近,车体刚度的变化会使传至车体的传递函数在频率上发生移动,但传递函数量值的改变并不大。
(5) 簧下质量的变化对轨枕至道砟的传递特性的影响最为明显,对由轮轨间传至钢轨的传递特性影响不大。

