定向反射膨胀装置作用特性研究
戴劲松,何 福,苏晓鹏,王茂森,谭 添
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.国营第152厂,重庆 400071)
利用后效期高速高压的火药燃气,炮口制退器可以有效地减小火炮后坐的能量,但其制退效率与声波、冲击波的矛盾仍未得到有效缓解。根据炮口制退器的作用原理,它通过改变后效期火药燃气的方向和速度,利用火药燃气对制退器产生向前的冲量达到减小火炮后坐能量的目的。但改变方向后的火药燃气会对炮位侧方区域带来不利影响,并且侧向流动的火药燃气会增加射击阵地被发现的几率[1]。
国内外相关领域的专家学者对炮口装置改变和控制火药燃气的流动状态做了许多研究。如苏晓鹏等[2]运用轴对称欧拉方程组和有限体积法,通过数值仿真对带某种炮口装置的火炮发射时膛口流场的情况进行仿真分析,与无炮口装置的情况对比,得到了某炮口装置对发射的影响。王永河[3]通过分析制退器的作用原理,对制退器高效率低危害的技术进行探讨,选出了某种新型结构的炮口装置并成功运用。王加刚等[4]通过射击实验对比,对某种新型高效低危害炮口制退器进行验证。Oswatitseh[5]对改进制退器的效率做了大量的理论和实验研究,曾经被誉为对炮口冲击波最好的工程研究。Chaturvedi[6]创新设计了可调式膛口制退器,在气体动力学理论的基础上通过数值模拟得到了制退力等参数,该设计可调性和创新性都略优于同类装置。
除了数值仿真的方法外,火炮上还常采用气体动力学理论与方法[7],建立相关气体动力学分析理论模型,特别是在正面设计时,更便于方案的确定和参数的选择。本文基于气体动力学理论,建立超高压气体定向反射膨胀的理论模型并进行数值计算,以确定实验装置的主要结构参数。在此基础上,构建实验装置,开展实验,验证了计算方法的正确性与可行性。
在现有炮口制退器研究的基础上,为了缓解炮口装置带来的影响,创新设计了定向反射膨胀装置,它通过在身管上开孔的方式,让火药燃气流入装置内,对装置产生向前的冲量,并在装置前端形成局部高压区,然后让燃气在装置内膨胀后流出。该装置减小后坐的原理与制退器类似,但改变了制退器安装在炮口的形式。相比较炮口装置依靠后效期火药燃气的作用,定向反射膨胀装置利用了部分内弹道和整个后效期的作用,并且在弹丸出炮口后,装置内有一定能量损失的燃气才开始向后定向泄流,从而达到与炮口装置减后坐的效率大致相同且对弹丸初速影响较小的效果。
1 物理模型
定向反射膨胀装置包覆在身管某位置,如图1所示,在装置与身管外壁之间形成空腔,让火药燃气在此作用。根据内弹道计算,选择火药燃烧结束点后的位置开孔,具体开孔位置结合内弹道膛压等参数确定。针对某30 mm火炮的射击情况,经过反复计算,确定开孔位置为平均膛压66 MPa处,上下共2个等效斜孔,与炮口水平方向呈30°夹角,孔直径为12 mm。如图2所示,当弹丸越过斜孔后,膛内火药燃气开始进入装置内,超高压气体对装置产生冲量并在装置前端产生高压区后反射膨胀,经过膨胀后的超声速气流在装置后端压缩减小速度,最后通过后端喷口泄流。

图1 定向反射膨胀装置三维示意图

图2 定向反射膨胀装置轴切面示意图
2 理论模型
针对定向反射膨胀装置的作用特点,运用一维准定常气体动力学理论建立其理论模型,作为以后分析的基础和起点。取弹丸刚通过斜孔时为初始位置,对此,根据相关计算经验做出假设:①流动是一维等熵的,且装置内气体均布;②气体从膛内刚通过斜孔时出现临界流动;③装置内气体波面运动速度等于波后的当地声速;④弹底火药气体速度等于当时弹丸运动速度。

图3 定向反射膨胀装置原理结构示意图
根据图3,将装置作用分为3个阶段,第1阶段,弹丸D越过斜孔C,膛内气体进入装置内,气流直接作用在A点内壁附近,向前后膨胀并在B0B1面反射;第2阶段,装置内气体在前端形成高压区并继续向后沿着B2B3B4膨胀,至后端出口B5,此时弹丸已飞出炮口;第3阶段,装置后端和炮口同时泄流。设x,x0分别为高压火药气体波面在装置内的轴向位移和弹丸在膛内的位移;v,v0,v1分别为装置内高压气体波面的运动速度、弹丸运动速度和斜孔处气流速度;p,p0,ps分别为装置内火药气体压强、膛内气体压强及弹丸刚过斜孔时初始位置膛内的平均压强;ρ,ρ0,ρs分别为装置内火药气体的密度、膛内气体的密度及弹丸刚过斜孔时初始位置膛内气体的密度;t为时间。
2.1 第1阶段分析
对于第1阶段,根据运动定律可得:
dx/dt=v
(1)
dx0/dt=v0
(2)
dv0/dt=ξ(p0Sd/md)
(3)
式中:ξ为弹丸有效功系数;md为弹丸的质量;Sd为炮膛横截面积。根据秒流量的定义,可得:
dm/dt=ρ0S1v1
(4)
式中:m为装置内火药气体的质量;S1为斜孔的等效面积。密度计算公式为
ρ0=(mz-m)/(Sdx0+V0)
(5)
ρ=m/Vq
(6)
式中:mz为装药量;V0为药室容积;Vq为装置内气体体积函数,根据装置具体尺寸可计算。结合假设条件和气体动力学临界流动相关知识,得:
(7)
式中:μ为考虑火药膨胀速度的修正系数;k为绝热指数。火药气体在装置内相对于波前气体是超声速流动,波面运动速度与波后当地声速相等,则:
(8)
根据等熵过程的关系式,可推出如下方程:
(9)
(10)
根据截面气流总反力的定义,定向反射膨胀装置所受的前冲量I可通过下式计算:
(11)
式中:Sq为装置内气体前冲量有效作用面积,可通过装置具体尺寸计算。联立式(1)~式(11)即为第1阶段求解方程组。
2.2 第2阶段分析
对于第2阶段,基本理论不变,需对个别方程进行修改。考虑斜孔处的流动情况,可分为正向临界流动、正向亚临界流动、反向临界流动和反向亚临界流动。设λ为满足临界流动时的压力比值,对斜孔处流速方程(7)修改如下:
(12)
装置所受的前冲量计算式(11)修改为
(13)
第2阶段的计算在第1阶段计算的基础上,将式(7)和式(11)替换为式(12)和式(13),其余方程不变。
2.3 第3阶段分析
在第3阶段计算中,设vpk为炮口气流速度;ppk0,ρpk0为弹丸出炮口时膛内气体的压强和密度;Sh,vh分别为装置后端喷口的等效面积和气流速度;m0为此阶段膛内气体的质量,等于装药量减去流入定向反射膨胀装置内气体的质量与炮口泄流的气体质量之和,则:
dm/dt=ρ0S1v1-ρShvh
(14)
dm0/dt=-ρ0S1v1-ρ0Sdvpk
(15)
ρ0=m0/(Sdld+V0)
(16)
ρ=m/Vh
(17)
式中:ld为整个内弹道弹丸行程长;Vh为装置容积。此阶段弹丸出炮口后定向反射膨胀装置和炮口开始泄流,炮口和装置后端喷口可以按照临界流动计算,可得:
(18)
(19)
斜孔处气流速度可按式(12)计算。根据等熵过程的关系式可推出下式:
(20)
(21)
此阶段装置所受到的前冲量可按式(13)计算。联立式(12)~式(21)可得第3阶段求解方程组。至此3个阶段的主要求解方程组全部列出,经数学推导整理后,最终形成一套闭环可解的微分方程组。具体推导的数学过程和得到的详细方程由于太过复杂,在此不再详述。
自选步长的四阶Runge-Kutta方法通过逐步比较计算精度,能帮助计算机自动选择计算步长,并快速计算出一阶常微分方程初值问题的数值解[8],上述微分方程组可运用该方法通过编写程序进行计算求解。
3 算例与验证
3.1 算例分析
针对某30 mm口径火炮,运用上述理论分析计算。已知该火炮内弹道数据,初速为960 m/s,弹丸质量为385 g。在身管1 320 mm处开孔,孔直径暂取12 mm,此时膛压为66 MPa左右,弹丸运动速度为865 m/s。假定沿身管轴线炮口方向为装置整体受力数值正方向,运用自选步长的四阶Runge-Kutta方法求解后,结果如图4~图6所示。
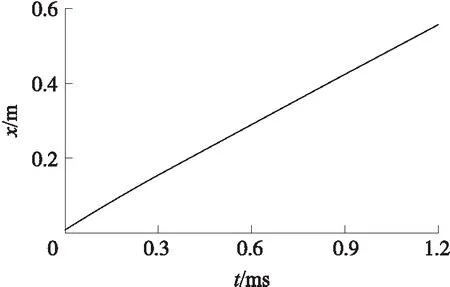
图4 装置内气体波面位移随时间变化曲线

图5 弹丸位移和速度随时间变化曲线

图6 装置整体轴向受力随时间变化曲线
根据该火炮内弹道数据可知,弹丸在计算初始位置约1.19 ms后出炮口。分析图4装置内气体波面位移随时间的变化可以看出,在1.19 ms装置内气体波面位移为559 mm,装置轴向长度为565 mm,也就是说弹丸出炮口后装置后端才开始泄流。图5显示,在1.19 ms时弹丸位移为身管长度2 300 mm,此时弹丸初速为953.9 m/s,与内弹道数据相比可以看出对初速的影响较小。对图6中受力曲线积分,结合制退效率的计算方法可以算得装置减后坐动能效率为20.1%。
通过分析可知,在后喷口封闭的情况下,定向反射膨胀仍能进行,只是其效率较有后喷口的低一些,仍有潜在应用价值,这方面将在其他的论文中分析。
3.2 实验验证
在该30 mm口径火炮上对定向反射膨胀装置进行实验验证,如图7所示。

图7 实验现场图
利用高速摄影拍摄发射过程中的情况,如图8所示,可以清楚地看到在弹丸已经出炮口、有燃气从炮口喷出后,定向反射膨胀装置后端才开始泄流,与数值分析结果相符。此外,相比传统炮口制退器在同样制退效率的情况,定向反射膨胀装置造成的火焰要小很多。

图8 发射过程高速摄影截图


图9 压电式压力传感器

图10 安装位置示意图

x/mmv/(m·s-1)vh/(m·s-1)原身管27.5960.03.65有实验装置24.4959.13.22
图11中,曲线最高峰数值为0.494 V,根据传感器说明书中相关指标,灵敏度为25.08 mV/MPa,可算得压力最高峰值为19.7 MPa,结合装置结构尺寸,此压力对应的力约为49 kN,与理论计算出力的最大值基本相符。表1中数据均为多发炮弹测量后的平均值,详细数据在此不一一列出。

图11 压电式压力传感器测量曲线
设正常自动机和安装定向反射膨胀装置的后坐体质量分别为mh和mfh,对应的后效期终了时的后坐速度分别为vh和vfh,则装置减后坐动能效率ηE为
(22)
将数值代入式(22),可以算得效率为22.1%。与理论计算的结果基本相符。在试验中,斜孔的孔径由小加大进行过多组射击,根据实验数据来看,加大孔径能有效提高定向反射膨胀装置的制退效率,在此不做详细讨论。由表1中弹丸初速数据可以看出,装置开孔对弹丸初速影响较小,符合数值分析结果。
4 结束语
本文根据定向反射膨胀装置的结构特点,对该装置建立了理论计算模型,根据理论分析研究了该装置的作用特性。针对某30 mm口径火炮,运用该理论解出了装置的减后坐效率和对弹丸初速的影响,并在该30 mm口径火炮上进行了实验验证,实验结果与数值分析基本一致,验证了本文对定向反射膨胀装置作用特性研究的正确性。
定向反射膨胀装置是基于减小火炮后坐力和减弱炮口制退器带来的不利因素的目的而设计的,该装置具有创新性并提供了新的思路。本文的分析为该装置的正面设计提供了依据,此外,通过分析可以知道影响该装置减后坐效率的因素有开孔位置、孔径大小、装置尺寸等,且通过适当的改变这些因素,定向反射膨胀装置的减后坐效率还有较大的提升空间,因此本文也为后续对装置的进一步修改与分析打下了基础。

