膜片式轻气炮破膜做功机理研究

沈吟青,江 坤,张 成

(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.上海宇航系统工程研究所,上海 201109)

轻气炮是一种利用高温低分子量气体(氢、氦)膨胀做功从而推动弹丸加速运动,使之获得极高速度的发射系统,是目前超高速发射领域内比较切实、可行的一种新概念发射技术[1]。自1946年第一门轻气炮诞生以来,关于轻气炮的研究日渐成熟[2-4]。美国多家拥有轻气炮设备的研究机构开展了大量超高速碰撞实验,其中GM通用汽车公司发射口径为5.6 mm的二级轻气炮可以将质量为0.053 3 g的弹丸加速至10.8 km/s[5]。管小荣等[6]通过建立数学模型,实现了二级轻气炮发射过程的理论计算,并得到结构和装填条件对发射性能的影响。庄宇等[7]通过建立了二级轻气炮轻气室部分的一维非定常可压缩流动模型来描述泵管内轻气的流动状况和弹丸的运动规律。隔离膜片作为轻气炮中控制整个发射系统的关键部件之一,故对其研究也变得越来越重要。王金贵[8]从选用材料和结构尺寸2个方面提出隔离膜片的相关设计要求。田慧[9]则提出隔离膜片的破裂压力可以控制活塞的启动时间,并影响药室内的最大峰压值。但在传统数值仿真研究中,对膜片破裂展开过程的研究相对较少,往往将该过程假设为膜片瞬间消失,忽略该过程对轻气炮内弹道性能的影响。

本文以一级双破膜式轻气炮中高压室与排气室之间的膜片作为研究对象,对膜片与膜片周围流场建立流固耦合模型,对膜片破裂后展开过程进行数值仿真,分析了膜片的动力学响应,揭示了膜片周围流场的发展规律;分析了不同因素对膜片展开过程的影响,为轻气炮膜片结构的设计与内弹道性能的优化提供重要参考。

1 流固耦合控制方程

1.1 结构域

结构域平衡方程为

(1)

式中:us为位移变量,ρs为结构密度,η为阻尼系数,σs为单元体柯西应力张量,fs为单位体积所受体力,其中,本文采用下标s表示固体域中的变量。考虑到模型中的大变形、高应变率问题,本文引入Johnson-Cook本构模型作为材料弹塑性阶段模型[10]。

Johnson-Cook本构模型由Johnson和Cook在1983年所提出,是一种可以描述延性材料在动态载荷作用过程中类似状态下的本构模型,适用于大多数金属材料,该模型弹塑性阶段表达式为

(2)

σ=A+Bεn

(3)

1.2 流体域

轻气炮膜片展开过程中,膜片两侧作为流固耦合边界经历的是一个大变形、大应变的过程。流体域N-S方程的任意拉格朗日欧拉(ALE)描述如下:

(4)

p=ρf(cp-cV)T

(5)

(6)

式中:V为控制体体积,S为控制体表面边界,n为控制体边界外法向单位向量,p为流体正压力,cp和cV分别为流体的定压比热和定容比热,ρf为流体密度,带下标f的量为流体域中的变量,v和w分别为流体的绝对速度和相对于网格移动的速度,E为流体单位体积总能,σ为粘性应力张量,I为单位矩阵,fb和qb分别为流体所受体力和单位体积产热量,q为外部传热热量。

流体本构方程为τ=-pI+σ。式中:τ为流体应力张量,而σ=2μs+λvI,s为变形速度张量,μ和λ分别为第一、第二黏性系数。

采用基于Petrov-Galerkin变分法的FCBI单元法对式(4)～式(6)进行离散:

(7)

(8)

式中:速度v、w分别采用不同的插值函数;温度θ、φ同样采用不同的插值函数。FCBI单元算法采用Galerkin法,对流项采用了线性插值与基于当地Reynolds数和Peclet数的非线性插值相结合的插值策略,降低了方程的非线性程度且提高了计算的稳定性。

1.3 耦合条件

在膜片表面流固耦合边界Si上需要满足运动条件与动力条件:

df=ds,ff=fs

(9)

式中:d,f分别为Si上的位移和应力。耦合方程表述为

(10)

式中:Xf和Xs分别为流体域和固体域解向量。耦合计算过程中,为了得到流体域内网格的位移,要用Lagrange坐标系对流体域的耦合面进行描述,通过插值使其与结构域耦合面上的位移保持一致。

采用直接法求解上述耦合方程,即将2个计算域的有限元离散方程组成统一的矩阵形式,每个时间步内采用Newton-Raphson法迭代计算。

2 膜片展开过程流固耦合分析

2.1 仿真模型建立

图1为一级双破膜式轻气炮结构示意图,本文的研究对象主要是高压室与排气室之间的隔离膜片Ⅰ。

固体域模型与网格如图2(a)所示。由于膜片发生破裂到凹槽完全撕裂历时较短,因此本文模型中初始时刻假设膜片已经沿着凹槽失效,即高压侧流体和低压侧流体已经在凹槽处连通。本文模型中膜片材料为304不锈钢,其材料的Johnson-Cook本构模型参数如表1所示[11]。膜片直径为200 mm,厚度为2 mm,采用三维实体单元离散。侧面设为约束边界,其余表面均设为流固耦合面。

图2(b)为流体域网格图。由于膜片流固耦合边界靠近压力入口边界,此部分流体流动相对复杂,因此对此部分网格进行加密。入口边界压力值为8 MPa,温度为273 K,低压侧初始压力值为3 MPa,温度值为293 K。流体类型选用高速可压缩流,高压工质选用氢气。

图2 网格模型

ABn2775660.794

2.2 结果分析

1)膜片应力分析。

图3为固体域膜片上应力分布图,显示应力主要集中在靠近膜片边缘的凹槽附近部分。

图3 膜片展开应力分布

图4为该部分A点的应力σ变化曲线,由图可知,该位置的应力随时间呈增长趋势。0.08 ms之前为弹性变形阶段,应力增速相对较快,到达屈服点后应力增速突降,进入塑性变形阶段。0.716 6 ms附近,膜片到达最大流通面积,A点应力趋于平稳,最大值为823 MPa。

图4 应力变化曲线

凹槽靠近边缘部分已经超过失效应力,实际加工时应对此部分加厚处理,来保证该部分具有足够强度,避免出现花瓣从膜片脱落的情况。

2)流场分析。

图5给出了膜片展开过程中周围流场的形成和发展过程。图中显示氢气射流高速流出进入排气室,初期膜片变形较小,展开所形成的射流入口面积较小,射流影响区仅在中心部分。初期阶段,高压侧流体泄入低压侧较少,两侧压差大小基本与膜片破裂瞬间相等,因此在入口处的压力梯度较大。两侧流体持续存在较大压差,膜片变形逐渐增大,射流入口面积也逐渐增大。

图5 膜片附近流场压力、速度分布图

在0.51 ms附近,可以看出中间射流影响区有所扩大,而周围部分的流速相对较小。膜片两侧的压差逐渐缩小,且入口处的等压线层次分明,压力梯度有所减小。随着排气室内的压力持续上升,在0.716 6 ms附近,膜片两侧的压差下降明显,因此膜片变形逐渐趋于稳定,且射流影响区达到最大。膜片此后不再运动,高压气体迅速流入排气室。在整个过程中,氢气射流的流速随时间逐渐增大,最大流速主要集中在射流区中心。

2.3 各参数对膜片展开过程的影响

为了进一步掌握膜片展开特性,本节分别分析了破膜压力、高压侧注气温度、膜片厚度、开槽形状等因素对膜片展开过程的影响。为方便分析膜片展开过程的流场特性变化,监测B点位移随时间的变化;同时在低压侧排气室内选取C截面,C截面距离膜片150 mm,监测C截面平均压力随时间的变化。

1)破膜压力对膜片展开过程的影响。

膜片的临界破膜压力是膜片的核心参数,其大小对膜片的展开过程具有较大影响。分别对4 MPa、5 MPa、6 MPa临界破膜压力条件下的膜片展开过程进行数值仿真,对应设置膜片展开时低压室初始压力分别为4 MPa、3 MPa、2 MPa,其余条件均保持一致。图6和图7给出了破膜压力分别在4 MPa、5 MPa、6 MPa时的B点位移v的变化和C截面平均压力pC的变化情况。

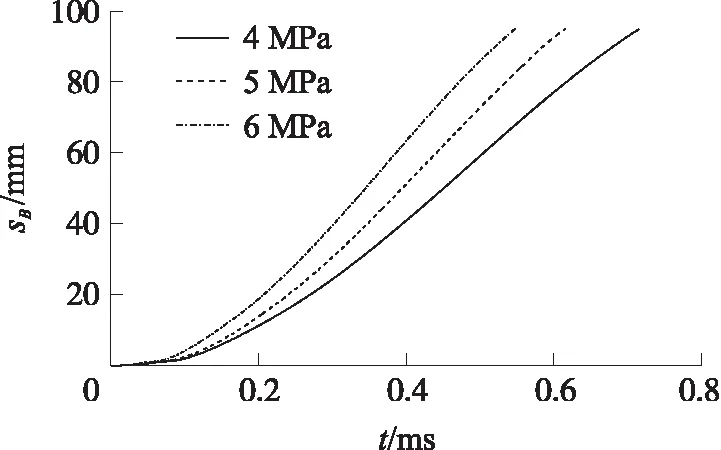
图6 不同破膜压力B点位移变化

图7 不同破膜压力C截面平均压力变化

由图可知,破膜压力差越大,膜片展开速度越快,排气室内的压力上升越快。膜片两侧压力差越大,整个系统的总能越大,在展开过程中转化成的膜片动能越大,高压流体流入排气室速度越快。其中,破膜压力为6 MPa时C截面平均压力上升速度比4 MPa时提高199%。

2)高压侧注气温度对膜片展开过程的影响。

取高压侧注气温度分别为273 K、573 K、873 K,其余条件均保持一致进行流固耦合仿真。由图8和图9可知,高压侧注气温度越高,B点位移速度越快,膜片展开速度越快,排气室内的压力上升速度越快。膜片高压侧注气温度越高,高压侧高压气体内能越高,整个系统的总能越大,在展开过程中转化成的膜片动能越大,高压流体流入排气室速度越快。其中,高压侧注气温度为873 K时C截面平均压力上升速度比273 K时提高19.8%。

图8 不同高压侧注气温度B点位移变化

图9 不同高压侧注气温度C截面平均压力变化

3)膜片厚度对膜片展开过程的影响。

图10和图11给出了膜片厚度分别在1.6 mm、2 mm、2.4 mm时的B点位移变化和C截面平均压力变化情况。由图可知,膜片越薄,展开速度越快,排气室内的压力上升越快。此外,由图13可以发现,厚度为2.4 mm的膜片最终位移比厚度为1.6 mm和2 mm的膜片小。膜片厚度较大时,造成最终展开角度较小,同时导致了排气室压力上升较慢。同时需避免出现花瓣从膜片脱落的情况,因此在膜片设计时,在满足强度要求的前提下尽可能减小膜片厚度。

图10 不同膜片厚度B点位移变化

图11 不同膜片厚度C截面平均压力变化

4)开槽形状对膜片展开过程的影响。

隔离膜片的预置凹槽普遍呈“十”字形,即在膜片表面加工四道凹槽,各凹槽之间的相差角度均为90°。考察采用不同开槽形状对膜片展开性能的影响,分别在开槽面预置六道凹槽和八道凹槽,并进行流固耦合分析,膜片固体域网格模型如图12所示。

图12 不同开槽形状固体域网格模型

图13和图14给出了不同开槽形状时的B点位移变化和C截面平均压力变化情况。由图可知,相比于其他2种开槽方式,开槽形状为六道凹槽的膜片展开速度最快,低压侧压力上升速度最快。因此,选用开槽形状为六道凹槽的膜片对展开过程最为有利。

图13 不同开槽形状B点位移变化

图14 不同开槽形状C截面平均压力变化

3 结束语

本文通过流固耦合分析方法对轻气炮中的膜片展开过程进行数值仿真,同时分析了不同因素对膜片展开过程的影响,主要结论如下:

①计算结果揭示了膜片周围流场结构的形成和发展过程,分析了膜片在高压工质作用下经历大变形的应力响应。

②破膜压力和高压侧注气温度对膜片展开过程影响显著,破膜压力越大,高压侧注气温度越高,越有利于膜片展开速度的提高和低压侧压力的提升。

③在满足强度设计要求的条件下,膜片厚度越小,越有利于膜片的展开;采用开槽方式为六道凹槽的膜片对展开过程最为有利。