随机时变车辆路径问题的多目标鲁棒优化方法

段征宇 ，雷曾翔 ，孙 硕 ，杨东援

（1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.上海市城市规划设计研究院，上海 200040）

车辆路径问题（vehicle routing problem，VRP）是物流配送的核心问题之一，研究如何安排车辆配送路线，使得配送成本最低.VRP 也是NP-hard（nondeterministic polynomial-time hard）问题，吸引众多学者进行了大量的研究工作.以往研究大多假定路段行程时间是常数或确定型时变函数.然而，随着城市交通拥堵的日趋严重，交通需求的短期变化、交通事故和恶劣天气等，导致了路网交通状态的不确定性.因此，在物流配送中需要同时考虑路网交通状态的时变性和随机性，以满足客户的时效性和时间窗要求，提高客户满意度.

随机时变车辆路径问题 （stochastic time-dependent vehicle routing problem，STDVRP）是研究在随机时变路网中，如何制定满足多个客户需求的配送车辆路径，使得总配送成本最小.STDVRP 是时间依赖型车辆路径问题 （time-dependent vehicle routing problem，TDVRP）和随机车辆路径问题 （stochastic vehicle routing problem，SVRP）发展而来，同时考虑了路段行程时间的时变性和随机性.在实际路网中，STDVRP 需要大量计算客户节点之间的最优路径，因此，随机时变最优路径问题 （stochastic time-dependent optimal path problem，STDOPP）是STDVRP 的基础.

早期STDOPP 研究以最小期望时间作为优化标准.比如：Hall[1]提出了分支限界方法与k最短路径相结合的求解方法，并发现由于不满足Bellman 优化原理，传统最短路径算法不能直接用于STDOPP；Miller-hooks 等[2]设计了求解最小期望时间路径的标号扩展算法.20 世纪90年代后，效用理论被引入最优路径的评价.比如：Wellman 等[3]提出了随机一致性条件，根据效用函数计算期望最短路径；Huang等[4]采用行程时间的负效用函数评价随机时变路径，设计了标号修改算法.以上研究以路段行程时间的概率分布为基础，求解算法的时间复杂度为指数形式，不适用于大规模路网.另一个思路是考察路段行程时间“最坏情况”下的“最优路径”.Sim[5]最早提出了鲁棒优化模型，将随机路网的最优路径问题 （stochastic optimal path problem，SOPP）转变为确定型路网的最短路径问题.Sun 等[6-7]将该方法扩展到STDOPP，将其转化为确定型时变网络的最优路径问题，求解算法的时间复杂度为多项式形式.

目前STDVRP 的研究相对较少，主要根据路段行程时间的概率分布，采用机会约束模型进行建模，使得期望行程时间最小[8-9].无时间窗STDVRP 的模型相对简单，但计算复杂度仍然较高，例如Nahum等[10]设计的遗传算法，对于100～200 个客户节点的STDVRP，平均计算时间为3.8 h.对于有时间窗STDVRP，需要考虑各客户的时间窗约束，求解更为困难，相关研究还很少见.

目前的STDOPP 和STDVRP 研究，通常需要知道路段行程时间的概率分布，求解的计算复杂度较高.对于实际路网的应用，要标定每个路段的行程时间概率分布是比较困难的.鲁棒优化方法提供了一种新的思路，已被成功应用于SOPP[5]、STDOPP[6-7]和SVRP[11].此外，目前大多STDVRP 研究针对无时间窗问题，而对于有时间窗问题，需要考虑各客户的时间窗约束，求解更为复杂.

本文建立了带硬时间窗的STDVRP 的多目标鲁棒优化模型，设计了一种蚁群算法进行求解.与传统的STDVRP 模型相比，该模型不需要知道路段行程时间的概率分布函数，只要根据历史交通数据标定其波动范围，在实际路网中使用更为方便.由于基于鲁棒优化模型的STDOPP，计算复杂度为多项式形式，因此，相比于基于路段行程时间概率分布的STDVRP 模型，鲁棒STDVRP 模型的计算复杂度更低.此外，该模型考虑了各客户的时间窗约束，与实际物流配送应用的情况更为一致.

1 STDVRP 建模

1.1 随机时变路网的表示和标定

对于随机时变路网G={V,A,T,Cab(t)}，其中：V为节点集合；A为路段集合；Cab(t)为路段lab在时段t（t∈T）的行程时间，如式（1），lab是从节点a到b的有向路段，lab∈A；T是时间分段的集合（1，2，· ··,M），M是路段行程时间函数Cab(t)的分段数.

式中：Rab(t)在 时段t是一个确定值；δab(t)是一个取值范围为[0,dab(t)]的 随机变量，dab(t)在时段t也是一个确定值.

因此，Cab(t) 的取值范围为 [Rab(t),Rab(t)+dab(t)].

假定随机时变路网G满足随机一致性条件[3].也就是，对于任意路段lab∈A，若t≤t′（t'为晚于t的另一个时段），对于给定时间ξ，式（2）成立，也就是出发时间早的车辆早到终点的概率比出发时间晚的车辆大.

随着浮动车技术的发展，获取城市路网的路段行程车速也越来越容易.例如，上海2007年建成的浮动车采集系统，接入了2.5 万辆出租车GPS 数据，可以计算得到各路段每5 min 时段的行程车速[12].采用历史数据，可以标定各路段每5 min 时段的行程时间的波动范围，从而得到路段行程时间函数Cab(t).

1.2 STDOPP 和STDVRP 模型的符号和变量

（1）常量

[0，te0]为配送中心的工作时间，开始时刻为0，结束时刻为te0；[tbi，tei]为客户节点i要求的时间窗，开始时刻为tbi，结束时刻为tei；tsi为客户i的服务时间；qi为客户i的配送需求量；Qk为车辆k的载重量；B为无穷大的数.

（2）集合

NS为始发节点集合；NE为终到节点集合；ND为需求节点集合；NSD为始发节点与需求节点的集合；NDE为需求节点与终到节点集合；NSDE为所有节点的集合；NSC为客户点集合的任一子集合，|NSC|为集合NSC的客户节点数；Λij为从节点i到j的可行路径的集合.

（3）决策变量和参数

K为使用车辆数；xij(t)为若车辆在时段t内出发，从i驶向j，值为1，否则为0；ti为配送车辆到达节点i的时刻；τi为配送车辆从节点i的出发时刻；vik为若点i由车辆k访问，值为1，否则为0；tij（τi）为时刻τi从节点i出发到j的最优路径的行程时间；λij为从节点i出发到j的一条可行路径（λij∈Λij）；f~(λi j,τi)为时刻τi从节点i出发到j，路径λij在最坏情况下的行程时间；lab为可行路径λij中的路段，即lab∈λij；yab(t)为若路径λij在时段t内经过路段lab，值为1，否则为0；t0k为车辆k从配送中心出发的时刻；tdk为车辆k返回配送中心的时刻.

1.3 STDOPP 的鲁棒优化模型

在STDVRP 中需要计算各客户节点之间以及客户节点与配送中心之间的最优路径，因此STDOPP是求解STDVRP 的前提.对于时刻τi从节点i到j的路径λij，最坏情况下的行程时间为

所以，根据最小最大准则，时刻τi从节点i到j的最优路径的行程时间为

根据文献[6]，结合式（3），可得

因此，时刻τi从节点i到j的最优路径的行程时间为

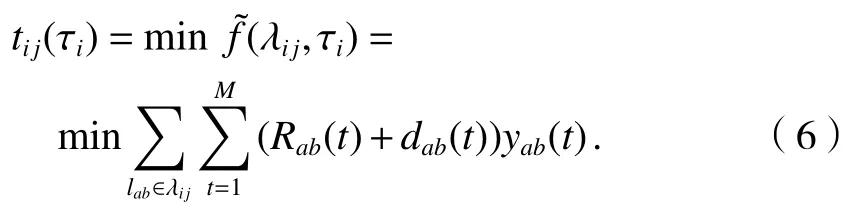
在式（6）中，Rab(t)+dab(t)是路段lab在时段t的行程时间上界，是一个确定值.若令Rab(t)+dab(t)为路段lab在时段t的行程时间，那么，可以得到一个确定型时变路网G′.可以证明G′是一个先入先出（first in first out，FIFO）网络[6].这样就将节点i到j的最优路径问题.转换为FIFO 时变路网的行程时间最小路径问题.传统最短路径的标号法可以用于求解该问题，并且时间复杂度为多项式形式.

1.4 STDVRP 的多目标鲁棒优化模型

下面给出带硬时间窗的STDVRP 多目标优化模型.硬时间窗约束要求在客户指定的时间窗内配送，先到必须等待，且不允许迟到.VRP 常用的优化目标有：使用车辆数最少、总行程时间最少、总等待时间最少、总行驶距离最小等.传统方法通常采用加权求和方法，将多个目标加权组合为单个目标进行求解.但由于量纲不同，多个目标之间往往不能直接比较，权重也很难确定.

对于STDVRP，总的配送成本主要由车辆固定成本、路径行程成本、客户惩罚成本组成.车辆固定成本与使用车辆数有关；路径行程成本与总行程时间有关；对于带硬时间窗的STDVRP，不允许违反客户时间窗要求，所以，不需要考虑客户惩罚成本.因此，在本文中选取使用车辆数最少、总行程时间最少两个优化目标，采用最小最大准则的鲁棒优化方法对STDVRP 进行建模.

（1）目标函数

使用车辆数最少：

总行程时间最少：

（2）约束条件

式（9）、（10）表示每个客户需要服务一次；式（11）、（12）表示同一条路线上的客户由同一辆车服务；式（13）表示每个客户只能由一辆车服务；式（14）表示每辆车的装载量不超过该车的容量；式（15）表示所有的车辆必须从配送中心出发，并返回配送中心；式（16）防止在配送路径中形成子回路；式（17）、（18）和式（19）分别是客户节点和配送中心的时间窗约束.

在上述STDVRP 模型中，客户点的时间窗和服务时间是固定的，客户节点i到j的最优行程时间tij(τi)根据1.3 节的式（6），采用路段在对应时段的行程时间上界计算，因此，该模型等价于求确定型时变路网G′的TDVRP.对于FIFO 网络的TDVRP，可以采用传统VRP 算法求解[13]，从而降低了STDVRP的求解困难.

2 STDVRP 的算法

Pareto 最优解也称为非支配解，是指不能再找到另外一些解，他们的所有目标都不差于Pareto 解的相应目标，且至少有一个目标优于Pareto 解的相应目标.Pareto 最优解通常是一个集合.设xA、xB是多目标优化问题 minY=[f1(x)f2(x) ···fm(x)]T的可行 解，若 ∀i1∈{1,2,···,m}，fi1(xA)≤fi1(xB)，且∃j1∈{1,2,···,m}，fj1(xA)＜fj1(xB)，则称xA与xB相比是Pareto 占优的，记作xA≺xB，也称xA支配xB[14].

STDVRP 属于NP-hard 问题，精确求解十分困难，通常采用亚启发式算法进行求解[10].

改进型非支配排序遗传算法（non-dominated sorting genetic algorithm II，NSGA-II）是Deb 等[15]于2002年提出的，在多目标VRP 问题求解中得到了成功的应用[16-17].由于本文已将STDVRP 转换为TDVRP，因此，可以用NSGA-II 算法进行求解.

蚁 群 算 法（ant colony optimisation，ACO）在TDVRP 中得到了成功的应用，可用于求解客户节点数量为100～1 000 的大规模TDVRP，具有较高的计算效率[18-20].本文将NSGA-II 算法中的基于Pareto占优的非支配排序引入ACO 算法，设计了求解一种多目标STDVRP 的非支配排序蚁群算法（nondominated sorting ant colony optimisation，NSACO）.

2.1 基于Pareto 占优的非支配排序

设解集P的规模为N，将P按照某种策略进行分级排序为m1个子集（P1、P2、…、Pm1），且满足：（1）∀i2,j2∈{1,2,···,m1}，且i2≠j2，Pi2∩Pj2=φ；（2）Pk1+1中 的可行解受Pk1的 可行解的支配（k1=1，2，…，m1-1）.快速非支配排序算法依据可行解之间的支配关系对P进行分级排序，将P划分为互不相交的子集.解集P的每个可行解设定两个参数ni2和Si2，ni2记 录支配可行解i2的 可行解数量，Si2是记录被可行解i2支 配的可行解的集合，令k1=1.算法步骤如下[21-22]：

步骤1计算每个可行解的ni2和Si2，找到解集P中ni2=0 的所有可行解，将其存入当前集合Pk1；

步骤2对当前集合Pk1中 每个可行解j2，考察它所支配的可行解集合S j2，将S j2中的每个可行解r2的nr2减去1（因为支配可行解r2的 可行解j2已经存入Pk1），若nr2-1=0则将可行解存入集合Q；

步骤3将Pk1作 为第k1级 非支配解集合，Pk1所有可行解的非支配序irank=k1，然后，令k1=k1+1，Pk1=Q；

步骤4若Pk1不为空，则转入步骤2，否则算法停止.

2.2 NSACO 算法

（1）初始化

采用文献[23]提出的初始解构造方法，生成质量较高的初始解，由此设定路段lab的信息素初始值ηab（0）.然后，采用“蚁周模型”更新规则[24]，对各路段的信息素进行更新.

（2）通过蚂蚁移动，构造配送路径，并进行局部信息素更新

每只蚂蚁从配送中心出发，根据“伪随机比例规则”[24]确定的转移概率，选择下一个节点：若满足约束条件，则选择该节点，并记录到禁忌表中，然后，对行经路段进行信息素更新；否则，返回配送中心，重新开始一条新的路径，直至所有客户节点都被访问，则该蚂蚁完成一次周游.

（3）全局信息素更新

在所有蚂蚁都完成周游以后，将得到的可行解与上次迭代保留的可行解合并，得到解集P；采用快速非支配排序算法，对P进行分级排序，得到第1 级非支配解集合P1；保留P1可行解，并对其行经路段进行信息素更新.路段lab的信息素ηab的更新方法如下：

式中：ηab（u）为第u次循环的当前信息素值；ηab（u+ 1）为更新后的信息素值；Δηab（u，u+ 1）为信息素增量；LP（u）为第u次循环，P1集合的可行解对应的总行程时间的平均值；ρ为信息素挥发系数.

为了避免出现“过早收敛”，采用“最大-最小蚂蚁系统”[25]的信息素更新策略，将路段信息素限制在[ηmin，ηmax]范围内.

式中：n为客户节点数；θb为选择最优解的概率，取0.05[25]；h（u）为第u次循环P1的可行解中最小的总行程时间.

（4）判断是否达到预定最大迭代次数，若符合，则输出最优解并结束计算；否则，返回步骤2.

3 算例分析

3.1 算例构建

Solomon 基准算例[26]在传统VRP 中被广泛使用，包括6 组共56 个算例.每个算例包括100 个客户节点，根据客户的空间分布，可分为3 类：C 类算例（聚集分布）、R 类算例（随机分布）和RC 类算例（混合分布）.参照文献[19]的方法，基于Solomon基准算例构建TDVRP 算例，然后，增加路段行程车速的波动范围，得到STDVRP 算例.具体如下：

将算例的路段分为5 类，路段lij的类型由g（i，j）表示，由式（24）确定.

表1给出了各类路段在4 个等分时段的行程车速.对时段1、3 的行程车速，增加±20%的波动范围；对时段2、4 的行程车速，增加±10%的波动范围，由此得到STDVRP 算例.为了方便仿真测试时计算期望行程时间和期望等待时间，假定路段行程车速的波动服从均匀分布.事实上本文的鲁棒优化模型和算法只与行程车速的波动范围有关，而与行程车速的概率分布形式无关.

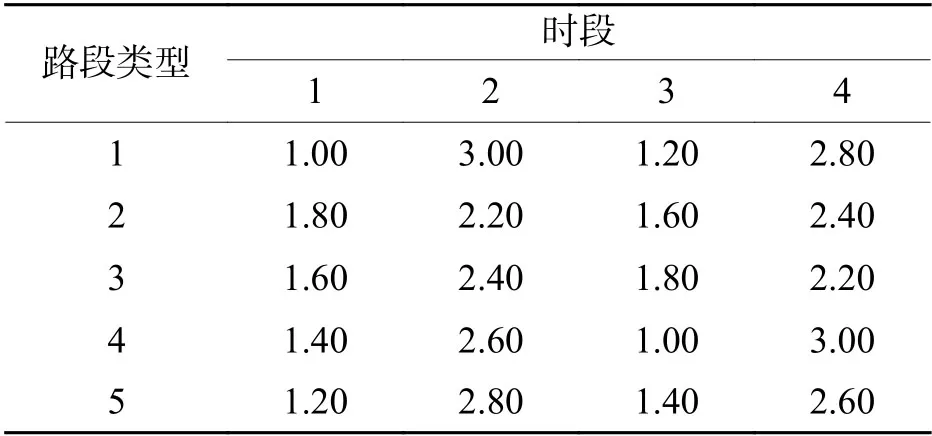
表1 各类路段的行程车速Tab.1 Travel speed of various links

3.2 Pareto 最优解集合及边界解

以扩展Solomon 基准算例R201 为例，采用NSACO 算法求解，得到的Pareto 最优解集合的分布情况，如图1所示.

Pareto 最优解集包含多个非支配解，为便于比较NSACO 算法和NSGA-II 算法的结果，仅选取边界解进行比较.为表述方便，将Pareto 最优解集中“最坏行程时间”最小的边界解称为“边界解A”，将“车辆数”最小的边界解称为“边界解B”.

3.3 算例求解

采用试算法确定NSACO 算法和NSGA-II 算法的参数，即每次给出某参数的一组取值，固定其它参数，根据算例的计算结果确定该参数的最优取值.得到NSACO 算法的参数：信息强度参数α= 1；能见度参数β= 2；信息素挥发系数ρ= 0.2；伪随机比例参数ω= 0.9；蚂蚁数量γ= 10.NSGA-II 算法的参数：交叉率取0.8；变异率取 0.2.两种算法的初始解均采用文献[23]提出的初始解构造方法生成.

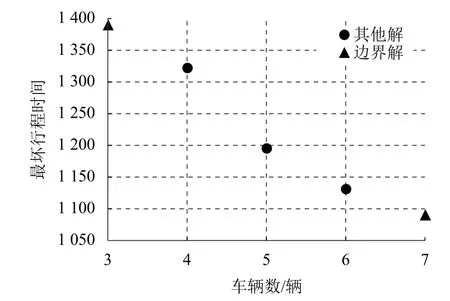
图1 R201 算例的Pareto 最优解的分布Fig.1 Distribution of R201’s Pareto optimal solutions

选取扩展Solomon 基准算例的C101、C201、R101、R201、RC101 和RC201，分别采用NSACO 算法和NSGA-II 算法进行求解，两种算法均迭代200次，得到各算例的Pareto 最优解集合.由于Pareto 最优解集合包含多个非支配解，为便于比较，这里仅给出“边界解A”和“边界解B”.

采用Monte Carlo 仿真的方法，根据表1的路段行程车速及波动范围，对最优解的配送执行过程进行模拟仿真，计算100 次，得到最优解的行程时间和等待时间的期望值.计算结果如表2所示.

表2 STDVRP 算例的计算结果Tab.2 Computational results of STDVRP instances

为了方便比较，将NSACO 算法最优解的结果除以对应的NSGA-II 算法最优解的结果，得到NSACO算法最优解的相对值，如表3所示.

根据表2、3，NSACO 算法的优化结果总体比NSGA-II 算法好.对于“边界解B”，尽管NSACO算法的最坏行程时间和期望行程时间比NSGA-II算法大4%左右；但NSACO 算法的车辆数比NSGAII 算法小3.33%.对于“边界解A”，NSACO 算法的车辆数、最坏行程时间和期望行程时间分别比NSGA-II 算法小11.98%、17.49%和23.03%.特别是对于C 类算例（C101 和C201），NSACO 算法的优化结果明显优于NSGA-II 算法.这是由于C 类算例的客户节点呈现聚集分布特征，能够更好地发挥NSACO 算法的信息素正反馈作用，相比于NSGAII 算法的随机搜索，NSACO 算法能更快搜索到最近的客户点.

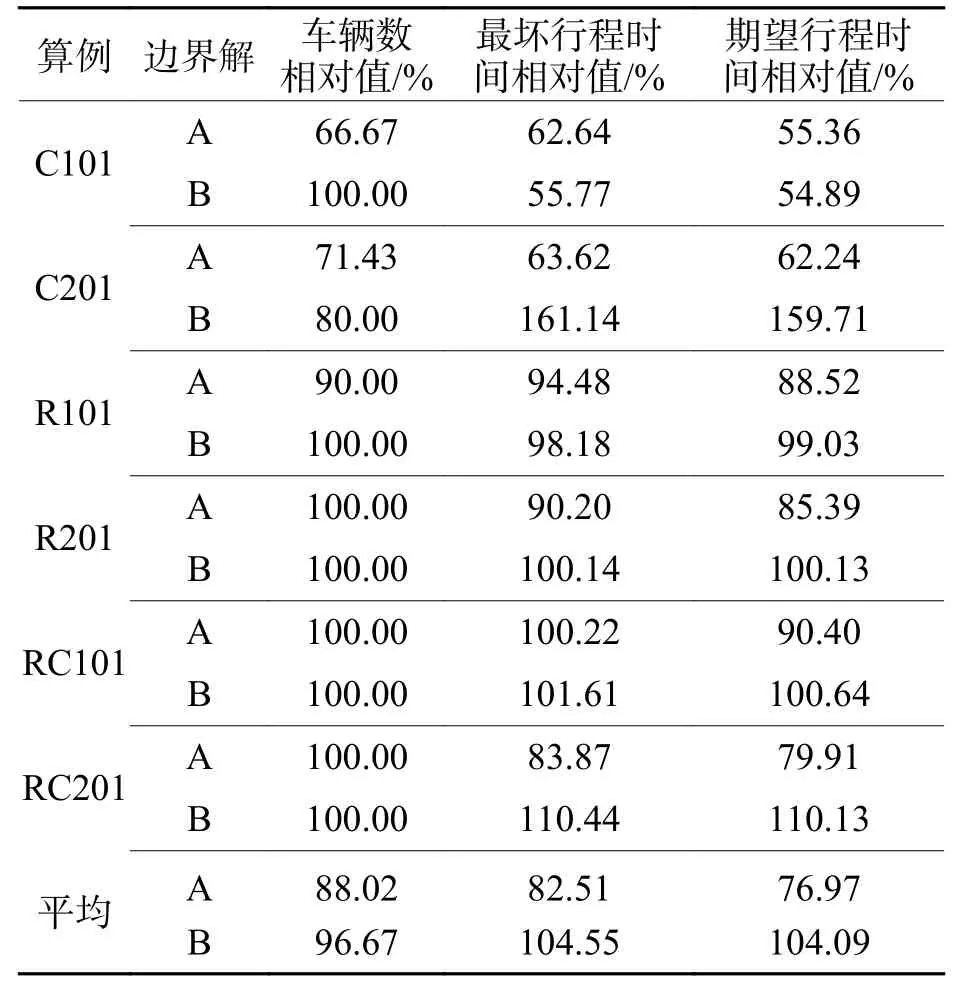
表3 NSACO 算法最优解的相对值Tab.3 Relative values of NSACO algorithm’s optimal solutions

4 结束语

本文针对带硬时间窗的STDVRP，提出了一种多目标鲁棒优化模型，并基于Pareto 占优的非支配排序方法设计了一种NSACO 算法进行求解.主要结论如下：

（1）多目标STDVRP 鲁棒优化模型可以转换为TDVRP，与基于路段行程时间概率分布的STDVRP模型相比，求解难度更低，适用于大规模实际网络的应用.

（2）STDVRP 测试算例表明，与常用的多目标NSGA-II 算法相比，NSACO 算法的优化结果更好.特别是对客户节点聚集分布的情况，NSACO 算法的收敛速度更快.

本文的STDVRP 鲁棒优化模型，只需要标定路段行程时间在各时段的波动范围，可以保证客户的时间窗要求，适用于大规模实际网络的物流配送应用.进一步的研究和改进包括：

（1）鲁棒优化模型主要考虑路段行程时间最坏的情况，得到的优化解偏保守，下一步研究将适度放宽时间窗约束和路段行程时间波动的上下界，综合考虑配送成本和准点送达率进行建模和优化.

（2）粒子群算法、鱼群算法等智能搜索算法在多目标优化领域也具有良好的性能，下一步工作将探索更好的多目标STDVRP 优化算法.