基于动力系统结构稳定性的共轭剪切破裂-地震复合模型

乔建永，马念杰，马 骥，赵志强，郭晓菲，师皓宇,3

(1.中国矿业大学(北京) 能源与矿业学院，北京 100083; 2.北京邮电大学 理学院，北京 100876; 3.华北科技学院 安全工程学院，北京 101601)

地震是自然界中经常发生的自然现象，是地壳断裂构造带演化伴随的产物，与地质断裂构造之间在几何特征和变化过程上具有相似性[1]。已有地震记录显示，许多地震区存在相互交叉的共轭发震断层，尤其强震的震源破裂往往呈“X”型共轭破裂，地震震中位于“X”型共轭破裂交汇部位[2-4]。美国加利福尼亚州Superstition Hills地震序列在2组共轭断层上同时出现地表破裂带[5];美国蒙大拿州Red Rock Valley体波震级Mb5.3地震震源深度12.4 km，位于Monument Ridge正断层和Red Rock断层的共轭交汇处[6];日本Kagoshima里氏震级M6.0地震(1997)发现共轭断层的存在，HORIKAWA等(2001)通过反演得出:共轭破裂起始于两断层段的交汇处附近并沿两侧传播[7];YUKUTAKE等(2008)由双差定位算法反演出主震震源与余震的位置，认为日本Niigata Chuetsu-Oki矩震级Mw6.6地震破裂主要发生在向东南倾斜的断层面上，主震的震源周围西北方向和东南方向倾斜的共轭断层面几乎同时破裂[8];CHEN等(2002)总结了台湾Chi-Chi地震(里氏震级ML7.3)的余震活动和震源机制表明，轻微东向倾斜的车龙埔断层和陡峭的西向倾斜的深层断裂带组成的共轭断层系统主导了震源区南部余震的空间格局[9]。

地壳中的断层活动诱发了地震，地震发生又促成了断层的生成与发育，通常认为断层的形成起始于地壳岩体的破裂。以此，学者们应用理论推断得到的各种震源模型来解析地震发生时震源区的力学行为。这些震源模型大体可分为两类，一类是假设作用在震源处有一组体力系的点源模型，如单力偶、双力偶和地震矩张量震源模型。双力偶震源模型普遍应用于定量分析断层错动引发地震产生地震波的特征，求解地震的两个断层面的走向、倾向及倾角，以及震源附近主应力方向等参数[10-12];地震矩张量震源模型可以描述各种形式的震源，如地下爆炸引起的体积膨胀源、地球内部介质体相变产生的快速扩展源或体积突然收缩源，断层错动等效的双力偶震源模型只是地震矩张量描述的各类震源中的一种[13]。点源模型是通过等效力的方法将地震震源假设受到一组力系和力偶矩的作用，缺乏实际的物理意义;另一类震源模型是非点源模型，主要有用震源处某个断层面的两侧发生位移或应变的间断来描述震源的地震位错模型、有限移动源(Haskell)模型、地震震源的裂纹扩展模型(Starr模型、Knopoff模型)、滑动弱化模型，描述地震震源破裂过程的障碍体(Barrier)与凹凸体(Asperity)模型，还有从摩擦强度的非均匀性入手，基于“弹性回跳假说”提出的弹簧-滑块动力学模型(Burridge-Knopoff模型)等[10,14-21]。尽管非点源模型对地震同震所引起的位移和应变等变化及其产生后果的分析成果很多，但仍然停留在理论研究的层面，尚未形成统一认识和进行实际应用[22-25]。

笔者从共轭剪切破裂演化过程中地震频发的表征现象出发，以动力系统结构稳定性理论中的Leau-Fatou花瓣定理逆定理和蝶形破坏理论[26-34]为理论基础，构建的“X”型共轭剪切破裂-地震复合模型，用于分析软弱异性体(如软弱岩体，破碎固体，融化岩浆等)周围岩体的应力变化;推导了破裂尺寸计算公式，给出了地震能量的计算方法，并建立起地震、能量、共轭剪切破裂之间符合逻辑的数学关系;推演出共轭剪切破裂的生成及演化机理、共轭剪切破裂-地震的发生及活动规律，明确了“X”型共轭剪切破裂-地震的物理意义，为研究断层-地震机理及其规律提供了全新的研究思路和方法，有助于丰富断层-地震研究的理论体系。

1 蝶形花瓣逆定理及其内涵

蝶形花瓣逆定理是孔洞岩体蝶形破坏和Leau-Fatou花瓣逆定理的总称。孔洞岩体蝶形破坏的概念来自于对圆形巷道围岩塑性区分布规律[28-31]、圆形巷道蝶型冲击地压机理[32-33]、巷道蝶型煤与瓦斯突出机理[34]的研究，认为巷道围岩出现剧烈变形破坏时围岩的破坏形状为蝶形。2000年乔建永研究平面复动力系统的结构稳定性问题，得到Leau-Fatou花瓣逆定理[26-27]，指出具有花瓣几何形状的不稳定点的出现，可以很好的描述具有突变特征的非线性复杂动力系统，即结构的突然失稳破坏。

1.1 岩体的蝶形破坏

文献[28-31]指出，处于高偏应力场中含有孔洞或软弱异性体(图1)的岩体将出现以软弱异性体为中心的蝶形破坏区，如图2所示，蝶形破坏区由4个蝶叶组成，分别位于最大主应力和最小主应力的两侧，两两对称分布;两个蝶叶轴线之间的夹角大体为80°～100°。图2中，Px，Pz分别为水平主应力与垂直主应力;σ1，σ2，σ3为微小单元体i的最大、中间与最小主应力。

图1 自然界中真实存在的软弱异性体Fig.1 Soft anisotropic bodies in nature① —软弱岩体;② —破碎固体;③ —融化岩浆

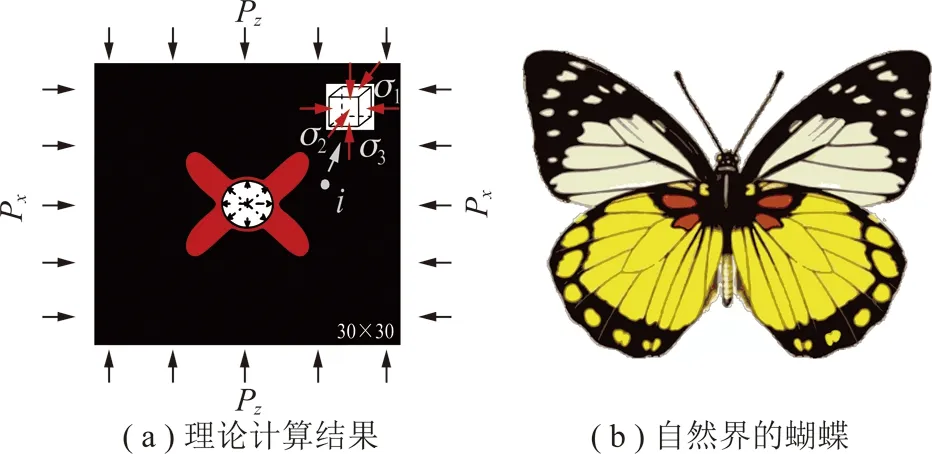
图2 高偏应力场中圆形孔洞周围的蝶形破坏Fig.2 Butterfly damage around circular holes in high deviated stress field

计算机数值模拟结果证明，无论软弱异性体是圆形还是矩形，甚至是各种不规则的其他形状，也无论软弱异性体周围岩体是均质还是非均质的弹性体，只要存在高偏应力场，都会出现蝶形或者残缺蝶形的基本破坏形态，如图3所示，数值分析模型为平面应变模型，具体尺寸为2 000 m×2 000 m(截取显示模型500 m×500 m);软弱异性体位于地下15 km，上覆岩层平均容重取27 kN/m3;通过采集原位地震波数据，实际观测出露地表的岩层组合剖面，以及实验室分析喷出火成岩的特性显示:大陆地壳10～25 km深处以变质岩或火成岩为主，且这一区域形成由花岗质(强碱性)片麻岩组合岩体逐渐向富含角闪相的镁铁质矿物组合过渡[35-36]。图3(a)，(b)反映不同形状((a)圆形与(b)矩形)软弱异性体围岩塑性破坏特征，且软弱异性体周围岩体为均质弹性体，力学参数与应力状态取值分别为弹性模量E=50 GPa;泊松比μ=0.25;黏聚力C=24 MPa，内摩擦角φ=46°;抗拉强度Rm=19 MPa;水平主应力Px=2 025 MPa;图3(c)，(d)中软弱异性体位于非均质层状岩体中，水平主应力Px取值分别为2 050 MPa和2 025 MPa，出现了蝶叶穿层与残缺蝶形破坏，岩层力学参数取值分别见表1,2。(注:参照煤的物理力学参数取值，图3中软弱异性体为软弱夹层，其自身的力学参数统一取E=1.27 GPa;μ=0.26;C=3 MPa;φ=18°;Rm=0.9 MPa)因此，对于软弱异性体周围岩体破坏规律的讨论，可以借用圆形孔洞周围的蝶形破坏理论结果。

表1 层状岩体的力学参数Table 1 Physical mechanics parameters of layered rock masses

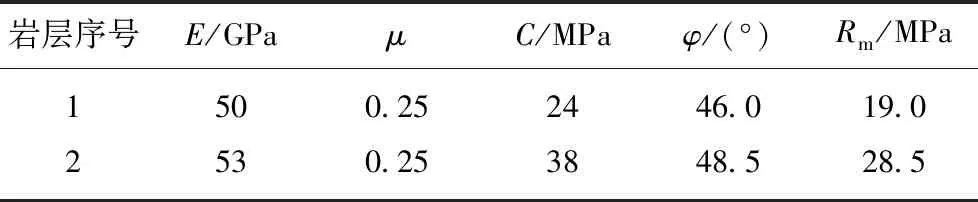
表2 坚硬-软弱互层的力学参数Table 2 Physical mechanics parameters of hard-weak inter-layers

文献[28-31]以摩尔-库仑破环准则为判定条件，推导得出含圆形软弱异性体围岩蝶形破坏边界的隐性方程为

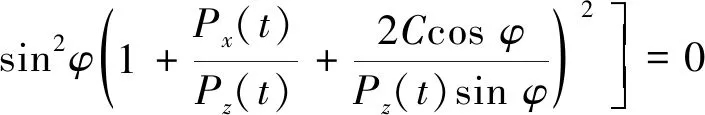
(1)

式中，a为规则圆形软弱异性体的半径;Px(t)，Pz(t)分别为软弱异性体围岩所受区域水平主应力和垂直主应力，是时间t的函数;q为软弱异性体的反作用力;r，θ为极坐标下的塑性破坏区边界半径和角度，θ∈[0,π]。

1.2 Leau-Fatou花瓣逆定理

花瓣图像[26-27]是指某点周围均匀分布若干个花瓣的数学图形，如图4所示。花瓣分为吸性花瓣和斥性花瓣，个数有奇数和偶数之分。

图4 奇数花瓣和偶数花瓣(5叶与4叶花瓣)Fig.4 Odd number and even number of petals(5 leaves and 4 leaves)

花瓣逆定理从区域的形状判断吸引轴和排斥轴的分布，同时指出:出现花瓣形状图像时将会发生非线性动力学现象。其核心是应用具有花瓣图像的数学函数准确描述系统对“初始值”的“敏感依赖性”，所谓对“初始条件的敏感依赖性”是非线性动力现象的一个普遍特征，表达的含义是:给定初始值的函数在复平面空间中的迭代轨迹，即使很微小的改变，如计算中由四舍五入产生的小误差，经过迭代可能变得放大了，当迭代到某种状态时微小的改变就导致整个系统灾难性的破坏，而花瓣形状图像就是这一迭代轨迹表现出的极端不稳定的几何形态，也就是说确定性系统内也存在着随机性的反映，在时间足够长之后，也可能有不可预测的现象发生[37]。因此，可以从数学角度解释自然界存在的稳定状态向非稳定状态的突变现象。

1.3 共轭剪切破裂-地震模型及其地震能计算

1.3.1共轭剪切破裂长度Rmax的计算模型

数值模拟分析的结果[28,30]表明，当蝶形破坏区范围较大时，破坏区的形状为“X”形状，与地质“X”型共轭剪切破裂相似，如图5所示，模型尺寸2 000 m×2 000 m，软弱异性体及其围岩力学参数与图3(a),(b)相同，水平主应力Px=2 180 MPa，垂直主应力Pz=405 MPa。所以，如果定义“X”型共轭剪切破裂由中心点向外扩展的长度为破裂长度Rmax，其中，Rmax为θ对应塑性破坏区半径r的极大值，则可以借用式(1)来进行计算，改写成简式为

Rmax=af(Px(t)，Pz(t)，C，φ，θmax，q)

(2)

1.3.2共轭剪切破裂-地震能量的计算

图5 软弱异性体周围破坏区的“X”形状Fig.5 “X” shape of the failure zone around the soft anisotropic body

对比图2和图4可知，蝶形破坏区形状与4叶花瓣具有相似性。所以根据Leau-Fatou花瓣逆定理可以推断，描述共轭剪切破裂长度的式(2)将出现由逐渐扩展到突然扩展的突变现象。由此还可以推断，基于图2的蝶形破坏区力学模型进行能量计算也将出现地震时能量突然释放的现象。因此，可以在蝶形塑性区理论模型的基础上通过能量计算，获得地震前后整个模型能量的变化情况，即计算在“X”型共轭剪切破裂扩展时释放的地震能。

任何弹性介质在受到外力作用时都会集聚弹性能，已知蝶形破坏区力学模型，设将该空间有界闭区域Ω任意分成n个子单元体ΔVi(i=1,2,…,n)，以ΔVi表示第i个子单元体的体积。微小单元体i受到3个主应力的作用，大小分别为(图6(a)):

σ1i≥σ2i≥σ3i

则该微小单元体的能量Ui为

2μi(σ1iσ2i+σ2iσ3i+σ3iσ1i)]ΔVi

式中，ui为微小单元体i的弹性应变能密度;Ei，μi，σ1i，σ2i，σ3i分别为第i个微小单元体的弹性模量、泊松比，以及最大、中间与最小主应力。

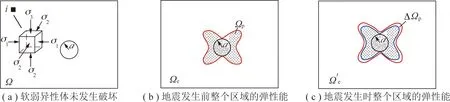
图6 地震能量的计算模型Fig.6 Seismic energy calculated model

地震发生前，软弱异性体及其周围岩体已经产生一定的塑性破坏，空间闭区域Ω转变为弹性Ωe和塑性Ωp(应力极限平衡)两种不同的区域，则子单元体分成ΔVe,i(i=1,2,…,m)，ΔVp,j(j=m+1,m+2,…,n)(其中Ωe∪Ωp=Ω)，i,j为弹性区与塑性破坏区的微小单元体变量，如图6(b)所示。(假设整个空间区域范围内，塑性破坏区Ωp的微小单元体仍处于弹性状态下)则整个空间闭区域的弹性能为

(3)

地震发生时，软弱异性体周围岩体塑性Ωp区域出现扩展，扩展时间为Δt，扩展范围为ΔΩp，整个空间闭区域的弹性能为

(4)

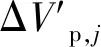
地震发生使得整个空间闭区域Ω的能量比前一时刻减小，这部分消耗的能量一部分用于岩石内结晶晶格错位，部分生成热量，还有一部分会引起岩体震动并以地震波的形式传播出去，即地震能。地震能其表达式为

Wm=β(Uep-U′ep)

(5)

式中，Wm为地震能，即地震发生时Δt秒释放的以软弱异性体围岩形成的蝶形破坏为震中的震源能(本文假设Δt=1 s)，106J;β为震动能因子，0<β<1，本文中β取值为0.5;Wm为一个以Px,y,z(t)为自变量的复合函数。

2 “X”型共轭剪切破裂形成机理及演化

2.1 “X”型共轭剪切破裂的形成机理

已建立的“X”型共轭剪切破裂-地震复合模型(图7)，及其推导得出的“X”型共轭剪切破裂长度的数学表达式(2)，可用于很好地定量描述共轭剪切破裂形成的力学机理:在高偏应力场作用下，软弱异性体周围会形成蝴蝶形状的高剪切应力区，该区域内的岩体与应力状态满足摩尔-库仑剪切破坏条件而遭到破坏，因而形成以软弱异性体为中心的“X”型共轭剪切破裂，“X”型共轭剪切破裂长度可通过式(1)，(2)求解。

由于数学力学分析方法的限制(无法完全按照自然界的实际条件进行解析)，为便于理论计算，假设软弱异性体为规则的圆形，位于地下深处h=15 km，半径a=10 m，纵向长度L=10 km，软弱异性体周围2.5 km半径范围内的岩体为花岗岩(图7)。容重取γ=27 kN/m3，软弱异性体周围岩体泊松比μ=0.25，弹性模量E=50 GPa，黏聚力C=24 MPa，内摩擦角φ=46°;破坏后塑性岩体泊松比μp=0.35;假设软弱异性体围岩处于均匀应力场中，即Px=Pz=γh=405 MPa(等压状态);为了分析的方便，设构造应力场变化中垂直主应力Pz(t)=405 MPa，并不随时间的变化而改变。则“X”型共轭剪切破裂-地震复合模型中只存在水平主应力Px(t)一个与时间有关的自变量，其余参数都已给出确定值。于是，令Pz(t)=405 MPa，Px(t)=2 583 MPa，a=10 m，C=24 MPa，φ=46°，q=202.5 MPa，可计算得到“X”型共轭剪切破裂的具体长度Rmax=r=303.55 m，如图7所示。

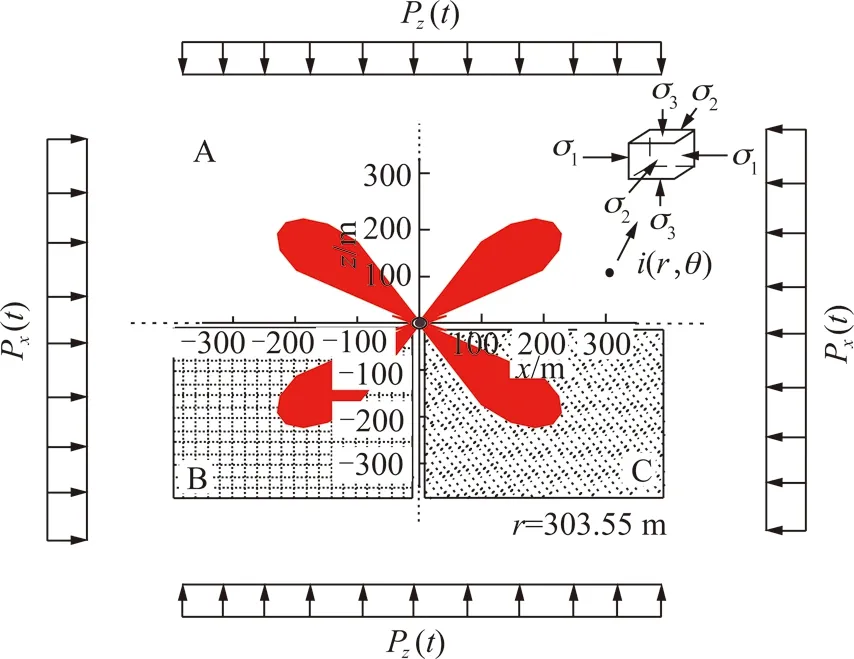
图7 “X”型共轭剪切破裂尺寸的计算结果(地下深处15 km)Fig.7 Calculational results of “X” conjugate shear fracture’s radius (It’s 15 kilometers underground)

2.2 “X”型共轭剪切破裂的演化特性

断裂活动和地震的发生都与集中于地壳内部构造应力场的作用密切相关[38]。以水平主应力Px(t)为自变量，通过公式(1)计算得到单位时间每增加1 MPa，“X”型共轭剪切破裂长度扩展变化量ΔR，如图8所示。以Px=Pz=405 MPa的等压状态为中心，曲线右侧:随水平主应力增大，ΔR呈正指数型增长;曲线左侧:随水平主应力减小，ΔR呈负指数型增长;定义曲线右侧随水平主应力增大形成水平高偏应力场为挤压应力区域，相应的随水平主应力减小形成的垂直高偏应力场为张拉应力区域;以挤压应力区为例进一步分析，当Px(t)≥2 583 MPa后(该拐点处曲线的斜率k=1)，对应的破裂长度增量ΔR变化曲线近乎与x轴垂直，此时已形成“X”型共轭剪切破裂(图5)，即数学上Leau-Fatou花瓣逆定理描述的4叶花瓣图形，则地壳软弱异性体与周围岩体组成的非线性动力系统对于“初始状态”具有敏感依赖性。也就是说，在一定地应力和围岩环境中，破裂的扩展对处于“初始状态”下的条件变化具有敏感依赖性，地应力和地层强度的微小变化将会引发“X”型共轭剪切破裂的不断扩展，有时甚至是剧烈扩展。

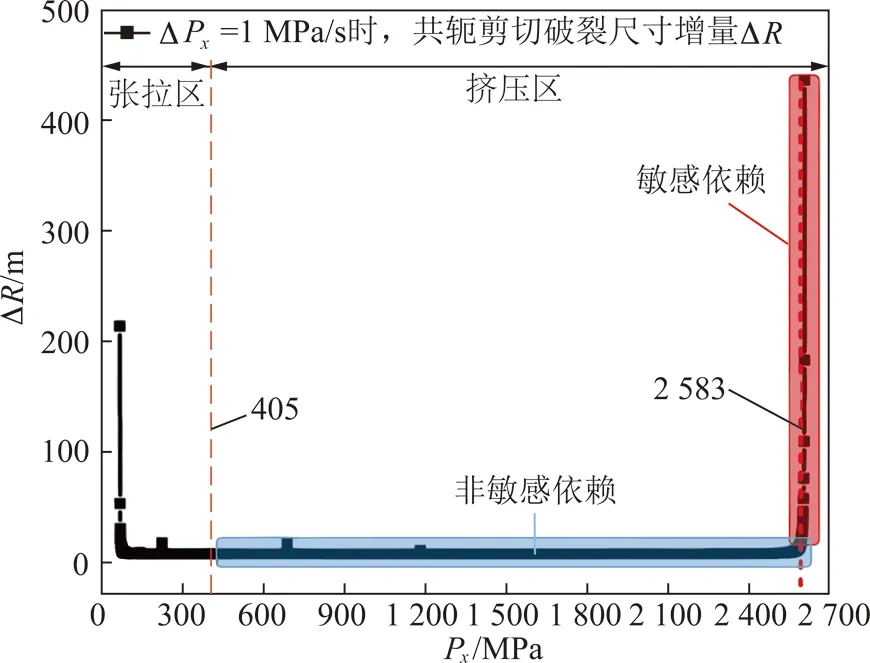
图8 水平应力增量为1 MPa时，破裂尺寸增量ΔR的变化关系Fig.8 Curves of the increment ΔR of fractures as the horizontal stress increment is 1 MPa

2.3 “X”型、“Y”型与“V”型共轭剪切破裂特征的成因

“X”型共轭节理(破裂)是一种普遍存在的节理系统，规模大，长度一般由数千米到十千米，最长30 km，表3所示理论计算得到的“X”型共轭剪切破裂尺寸Rmax与自然界中真实存在的“X”型共轭剪切破裂长度相吻合[39-40]。地质学家通过露头地层剖面记录到复杂的共轭破裂体系整体呈“X”型、“Y”型和“V”型的共轭特征[41]，可由式(1)的计算结果很好地定量解释。如图7所示，当A,B和C区域都为软弱岩层时，软弱异性体周围岩体会呈现出“X”型共轭破坏特征;如果B,C为强度高的坚硬岩层，软弱异性体仍然位于软弱岩层A中，则共轭剪切破裂的发展会受到坚硬岩层的阻断，从而形成“V”型共轭破裂。位于犹他州汉克斯维尔的Entrada和Curtis地层中共轭破裂的现场观测充分证实了这一点:“V”型共轭破裂交叉点集中在富含淤泥的软弱地层中并沿着软弱岩层发育明显[42-43]。数值模拟反演结果也普遍证实了:破裂交叉点附近的几何特征和软弱岩性夹层可能对共轭破裂的生长和发展产生强烈影响[43];当共轭剪切破裂某个发展方向上岩体强度比软弱异性体周围岩体的强度高(图7中C区域为坚硬岩层，A,B区域为软弱岩层)，则该方向的破裂发展就会受到限制，从而呈现出“Y”型的共轭特征;如果软弱异性体周围只有一个方向上为软弱岩层(图7中B为软弱岩层，其余区域为坚硬岩层)，则会形成单个的破裂特征。综上分析可知，共轭剪切破裂的扩展对于地层强度的微小变化具有敏感依赖性，它既可以引发“X”型共轭破裂的不断扩展，也可以使得花瓣缺失或残缺，出现不完整蝶形的形态，即软弱异性体周围岩体强度特征变化，使得共轭破裂表现出“X”,“V”,“Y”型共轭特征，图9数值模拟结果充分验证了理论分析的真实性。其中，数值模型、应力条件、规则圆形软弱异性体尺寸及围岩力学参数(选用图3(d)的参数)如图3所示。

表3 不同水平主应力对应“X”型共轭破裂尺寸的计算结果Table 3 Calculational results of different horizontal principal stresses corresponding to “X” conjugate fracture’s radius

注:假设Pz=405 MPa;q=202.5 MPa。

图9 不同类型共轭剪切破裂形成的数值模拟结果Fig.9 Numerical simulation results of shear fractures formation of different types

3 地震与“X”型共轭剪切破裂一次性扩展尺寸的关系

在“X”型共轭剪切破裂-地震复合模型及共轭剪切破裂尺寸数学表达(式(2))的基础上，从数学上推演得到的地震释放能量计算式(5)，可以明确“X”型共轭剪切破裂一次性扩展长度与地震释放能量大小的关系。如图10所示，当水平应力增量ΔPx=1 MPa/s时，应用式(2),(5)分别计算得到共轭剪切破裂尺寸一次性扩展量ΔR、地震释放能量Wm和相应里氏震级ML。分析表明:随水平主应力Px的变化，地震释放能量Wm与地震震级ML具有同共轭剪切破裂一次性扩展量ΔR相同的指数型增长趋势;同时可以看出，ΔR和Wm都是水平主应力Px的单值函数，二者之间是一一对应关系。当图中的水平应力不断增加或减小，“X”型共轭剪切破裂也在不断扩展，“X”型共轭剪切破裂尺寸与地震释放的能量相对于水平主应力Px的变化具有同步性，地震与“X”型共轭剪切破裂扩展之间为相互伴生关系，它们同时出现，也同时消失。

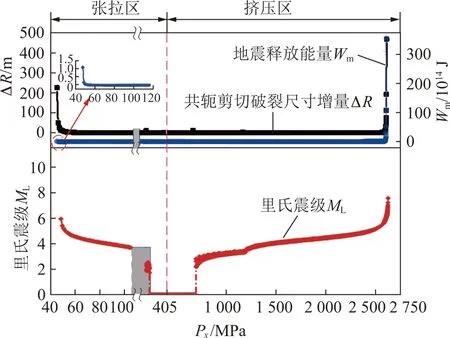
图10 破裂尺寸一次性扩展量、释放能量与地震震级Fig.10 One-time expansion of the size of fractures,release energy and seismic magnitude

表4为不同破裂尺寸条件下水平应力扰动为0.1 MPa时，“X”型共轭剪切破裂尺寸增量ΔR、地震能Wm与对应里氏震级计算结果，围岩力学参数与图3数值模拟选用参数保持一致。可以看出，“X”型共轭剪切破裂扩展一次释放的能量级别可以涵盖自然发生的各种地震震级和每次地震震中释放的能量;相同的应力扰动在不同的应力状态下引发“X”型共轭剪切破裂一次性扩展的尺度不同，从而引发不同级别的地震(例如水平应力Px=2 591 MPa时，增加0.1 MPa，破裂一次性扩展2.4 m，释放的能量量级可达1013，相当于里氏6.0级地震)。对于一般地质力学条件下“X”型共轭剪切破裂引发地震的能量计算，式(5)同样适用，而且会得出与本文给出的完全相同的结论。

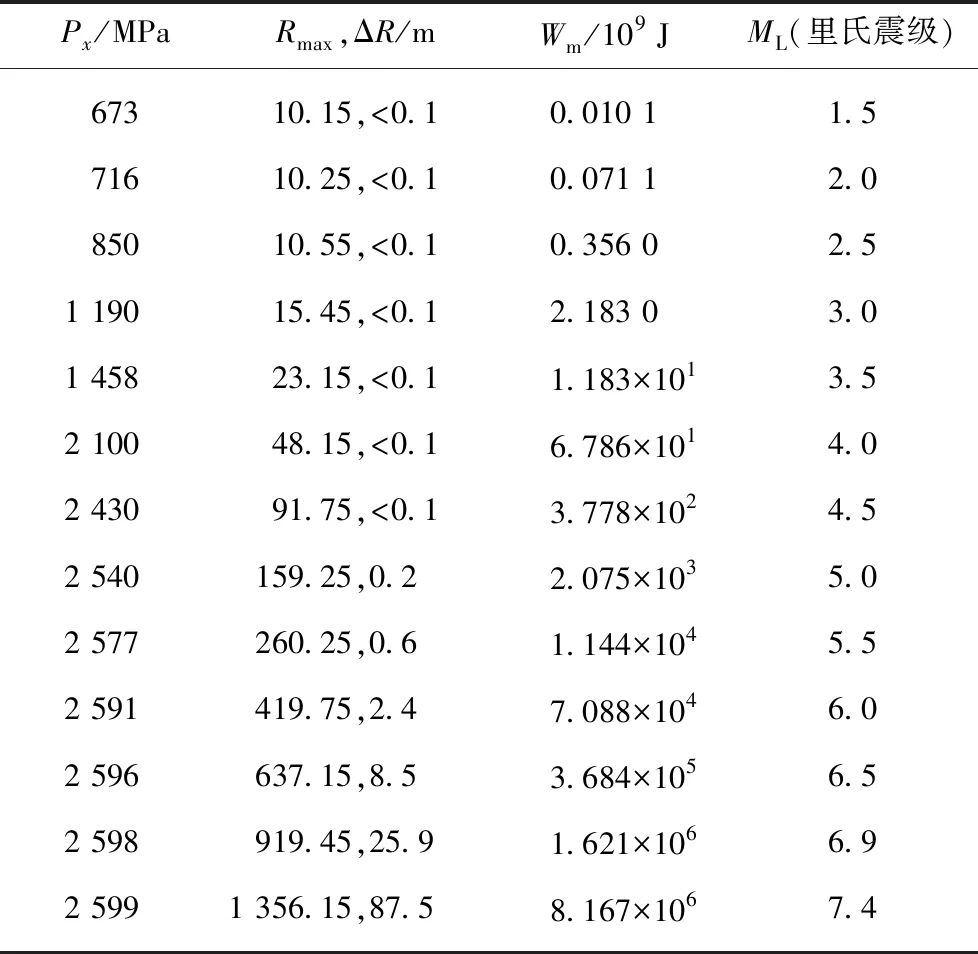
表4 “X”型共轭剪切破裂尺寸增量ΔR、地震能Wm与对应里氏震级计算结果Table 4 Calculational results of increment ΔR of “X” conjugate fracture’s radius,seismic energy Wm and corresponding Richter Magnitude

4 自然地震对微小应力的敏感依赖

“X”型共轭剪切破裂-地震复合模型用定量方法解释了许多微小应力变化触发自然界中较大地震的现象。根据式(5)可以求得不同应力环境下，水平应力扰动分别为1，10-1，10-2，10-3，10-4，10-5，10-6，10-7和10-8MPa/s时，引发地震所释放的能量与对应的震级(里氏震级通过公式lgE=11.8+1.5Ms换算得到[44],Ms为面波震级，见表5)。需要指出:地应力本身是没有时间概念的，水平应力扰动是有作用时间的，文中水平应力扰动是以秒为单位，反映出每秒释放的能量。由表5可以看出，对于相同应力状态的“X”型共轭剪切破裂来说，扰动应力ΔPx值越大则发生地震的震级越高。相同于“X”型共轭剪切破裂扩展对应力状态和区域围岩强度的敏感依赖性，地震对于“X”型共轭剪切破裂所处的应力状态和区域围岩强度(震前状态)也同样具有敏感依赖性，微小、甚至极其微小的应力扰动即可触发大级别的自然地震，很好地解释了自然界中普遍存在的仅仅0.01 MPa甚至更微小的应力变化触发地震的现象[45-47]。例如，苏门答腊-安达曼地震(M9.0，2004)(the Sumatra-Andaman earthquake)震后仅0.01 MPa的局部应力扰动就引发附近M8.6地震[48];汶川M8.0地震发生后，与其震中相隔85 km的庐山地震(Ms=7.0)前后应力变化0.02～0.04 MPa(0.2～0.4 bar)[49];甚至距离3 100 km处Mw=7.9Denali地震震中(美国阿拉斯加)产生的0.16～0.22 MPa动态触发应力，亦可引发有感地震[50];日本北部Iwate火山岩浆膨胀使得区域应力场发生变化，0.33 MPa的应力增加引发了Ms=6.1级地震[51];此外，平均量级103Pa的固体潮汐应力、地球自转以及人类活动等产生的应力扰动也可对地震的发生产生重要影响[52-55]。

表5 不同触发应力Px，地震能Wm与对应里氏震级计算结果(围岩力学参数选取同表3,4)Table 5 Calculational results of different trigger stresses Px,seismic energy Wm and corresponding Richter Magnitude (The surrounding rock mechanics parameters are shown in Table 3,4)

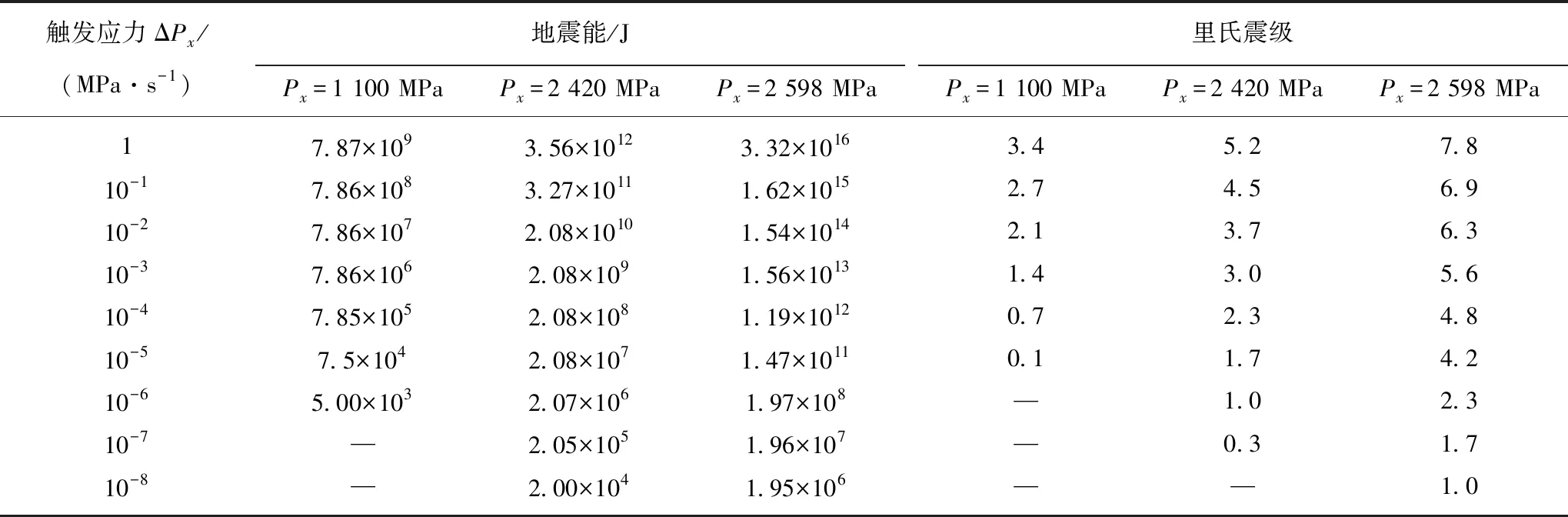
表5 不同触发应力Px，地震能Wm与对应里氏震级计算结果(围岩力学参数选取同表3,4)Table 5 Calculational results of different trigger stresses Px,seismic energy Wm and corresponding Richter Magnitude (The surrounding rock mechanics parameters are shown in Table 3,4)

触发应力ΔPx/(MPa·s-1)地震能/JPx=1 100 MPaPx=2 420 MPaPx=2 598 MPa里氏震级Px=1 100 MPaPx=2 420 MPaPx=2 598 MPa17.87×1093.56×10123.32×10163.45.27.810-17.86×1083.27×10111.62×10152.74.56.910-27.86×1072.08×10101.54×10142.13.76.310-37.86×1062.08×1091.56×10131.43.05.610-47.85×1052.08×1081.19×10120.72.34.810-57.5×1042.08×1071.47×10110.11.74.210-65.00×1032.07×1061.97×108—1.02.310-7—2.05×1051.96×107—0.31.710-8—2.00×1041.95×106——1.0

5 结 论

(1)应用“X”型共轭剪切破裂-地震复合模型的理论计算结果推演了共轭剪切破裂形成的力学机理:在高偏应力场作用下，软弱异性体周围岩体会形成蝴蝶形状的高剪切应力区，该区域内的岩体与应力状态满足摩尔—库仑剪切破坏条件而遭到破坏，因而形成以软弱异性体为中心的“X”型共轭剪切破裂。

(2)软弱异性体周围岩体强度特征变化，使得共轭破裂表现出“X”,“V”,“Y”型共轭特征;共轭剪切破裂尺寸一次性扩展与地震释放能量具有同步性，即地震与“X”型共轭剪切破裂是相互伴生关系，它们同时出现，并同时消失。

(3)在实际地层中存在某种地应力环境，使得地壳软弱异性体与其周围岩体组成的非线性动力系统对于“初始状态”具有敏感依赖性，“初始状态”可以是软弱异性体自身的形状、尺寸，也可以是所受应力环境和周围岩体物理力学性质。也就是说，某些情况下，地应力的微小变化会引发“X”型共轭剪切破裂的较大扩展和较大地震。