基于蝶形破坏理论的地震能量来源
马 骥,赵志强,师皓宇,3,郭晓菲,乔建永,2,马念杰
(1.中国矿业大学(北京) 能源与矿业学院,北京 100083; 2.北京邮电大学 理学院,北京 100876; 3.华北科技学院 安全工程学院,北京 101601)
地震是地壳板块运动时快速释放能量过程中造成的急剧震动,并会产生地震波的一种自然现象。地震过程的第1阶段,即在地球内部能量激发的起因,至今仍是众说纷纭,并没有形成统一的认识。自20世纪初,科学家们就地震的能量来源,相继提出弹性回跳、相变和岩浆冲击3个比较有影响的假说[1-2]。弹性回跳假说详细并系统地总结了地震的成因与能量的来源,即地震是地壳岩体突然断裂错动引起的,接着岩体又沿着断裂面整体弹性回跳到初始状态,地震能量来源于断层两侧岩体发生不均匀弹性变形所产生和积累的弹性变形能[3];相变说揭示的能量来源于地下物质由于临界温度和压力作用下,其自身密度增大体积突然变小,发生相变,周围岩体由于应力状态发生改变,快速挤压该相变物质从而激发地震波[4];岩浆冲击说认为地震能量是地下深处高温高压的岩浆涌入地壳,使得地壳岩体导热不均,部分岩体体积膨胀挤压周围岩体,导致周围岩体发生破裂激发的地震波[5]。
受三大经典假说影响,后来学者针对不同类型地震分别提出了一系列假说,试图揭示地震能量来源。黏滑说基于弹性回跳假说将断层变形问题转化为断裂两侧岩体的摩擦问题,指出地球上的浅层地震(深度<70 km)为新老断层滑动过程中的黏滑,地震能量来源于相邻震区提供给震源体的应变能[6-8];既然因断层运动导致岩石破裂就能引发地震,研究岩石本身破裂机制十分必要。岩石破裂说提出断层面上存在障碍体与凹凸体破裂模型,地震发生能量来源于积累高能量载体自身突然破裂[9-10];剪切熔融假说认为地壳岩体在剪切应力持续作用下发生蠕变,在蠕变加速过程中岩体变形并集中在一个具有高速蠕变特征的薄层中,该薄层由于温度升高产生熔融进而导致沿剪切带滑移,最终由于耗散产生剪切失稳发生地震(深度>300 km),此过程描述了地震的能量主要来源于高速蠕变的薄层温度升高使得局部岩体弱化存储的能量[11];脱水脆裂假说解释板块在俯冲过程中将一定数量的水带入地球深部,随深度增加温度和压力不断增大,当达到一定的温压条件时引起矿物脱水脆化破裂,以弹性波的形式释放积聚的弹性变形能进而引发地震(70~300 km)[12];反裂隙断层假说基于相变说的论述,指出地震能量来源于超高压作用下,深源岩体内部反向裂隙贯通形成断层时以弹性波形成释放的弹性应变能[13];孕震断层多锁固段脆性破裂理论认为孕震断层存在一个或多个锁固段,强度高的锁固段承受应力集中,是高能量的载体,发震能量主要集中于此;某个锁固段发生宏观破裂后,应力向下一个锁固段转移,导致下一个锁固段承受应力集中,以此类推[14];重力塌陷假说解释地震能量来源于震源岩体直接释放出的重力位能,能量的大小取决于作用在震源岩体上的重力所产生的构造应力[15];地球自转速率的加强或减慢触发板块构造运动,使得板块边缘与构造聚集带地震活跃,揭示了地震能量与地球自转有关系[16];共振假说指出地震能量主要来源于震源区岩体自身的自由振动周期与天体、太阳以及地球自转产生的某些周期相一致或接近整数倍时产生共振做功所积累的动能[17]。这些假说对人们从宏观上认识地震的能量来源提供了良好借鉴。
近期出现的蝶形破坏理论[18-20]可以从微观角度认识地震的发生机理和能量来源,它较好的解释了煤矿巷道冲击地压发生机理[21-22]与掘进巷道煤与瓦斯突出的机理[23],为地震能量来源的研究提供了一种新方法。笔者首先从软弱异性体周围岩体发生塑性破坏引发能量改变角度出发,构建地震发生时以软弱异性体为中心的能量分析模型,提出地震震源能与地震能的计算方法;然后,采用FLAC3D数值模拟手段理论分析地震发生过程中能量积聚与释放的变化特征;最后,对比分析真实地壳应力环境下有无软弱异性体存在,地震震源能分布特征与触发地震能的变化特征,阐明不同类型(形状、尺寸与性质)软弱异性体存在所揭示规律的一致性,及能量分析模型与计算方法的合理性与适用性。
1 地震能量来源的理论分析
1.1 均匀弹塑性介质中软弱异性体围岩的能量分析模型
地震时会释放大量的能量,研究地震发生机理,首先需要弄清地震的能量来源。受蝶形破坏理论的启发[18-20],考虑从软弱异性体周围能量集中现象进行分析,如图1所示,这里的软弱异性体是指真实地壳岩体中存在着的强度较低、具有一定尺寸,任意形态特征,可能充斥有气态、液态物质的软弱岩体、破碎固体等,是一个广义的概念。

图1 自然界中真实存在的软弱异性体Fig.1 Soft anisotropic bodies in nature
由于软弱异性体的存在,周围岩体应力将重新分布,形成围绕软弱异性体周边的应力集中。应力的变化也带来了软弱异性体周围岩体中能量分布的变化,即能量集中。由弹性力学理论可知[24-25],集中在软弱异性体周围岩体内的弹性能可以通过原岩应力和周围岩体的物理力学参数计算出来。为此,构建了软弱异性体存在发生塑性破坏集中与释放能量的计算分析模型如图2所示。
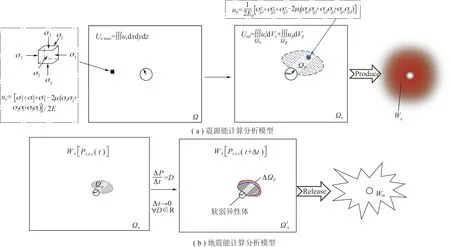
图2 软弱异性体周围能量计算分析模型Fig.2 Computational,and analytical,model for energies around a soft anisotropic body
1.2 含软弱异性体围岩集中弹性能的计算
板块构造学说认为:划分板块的岩石圈具有较高的刚性和弹性(均厚70~80 km),漂浮在低密度、塑性软流圈之上作大规模运动[26]。因此,对地震过程有意义的弹性应变能可等效为引起岩石圈体积发生变化的体变能。当应力和应变满足线性关系时,岩石圈任意微单元体均满足虚功原理[27],则微单元单位体积应变能,即应变能密度可表示为
(1)
其中,σ1,σ2,σ3分别为区域应力场主导下的最大,中间与最小主应力;E为均质岩体的弹性模量;μ为岩体的泊松比。如图2(a)所示,假设大尺度的地质体为理想弹性体,则其空间内任意一点的应变能密度可由式(1)计算(软弱异性体及其周围岩体构成空间闭区域任意单元的应变能密度)。当含软弱异性体围岩出现破坏后,其塑性破坏区的微小单元体仍看作处于弹性状态下,则该区域弹性应变能密度可等效用式(2)计算(此时的弹性模量与泊松比为塑性状态下的量值)。
σp2σp3+σp1σp3)]
(2)
式中,σp1,σp2,σp3分别为塑性破坏区域微小单元受到的最大,中间与最小主应力;Ep为该区域岩体的弹性模量;μp为塑性破坏区岩体的泊松比。软弱异形体与其围岩共同构成空间闭区域Ω(规则圆形软弱异形体半径a的5倍以上范围),当软弱异性体围岩没有出现任何破坏时其弹性应变能最大,表示为
(3)
塑性破坏区出现后,必定消耗能量,这就意味着图2的能量计算模型存在着弹性Ωe和塑性Ωp(应力极限平衡)两种不同的区域,其中Ωe∪Ωp=Ω。则在软弱异性体周围部分岩体出现破坏后,含软弱异性岩体的全部弹性应变能用Uep表示,即
(4)
式中,u′e,up分别为弹性区Ωe与塑性区Ωp的微单元单位体积应变能密度;dVe,dVp为对应微单元的单位体积。
含软弱异性体的最大弹性应变能Uemax大于软弱异性及其周围岩体破坏后的弹性应变能Uep,这一差值伴随着软弱异性体围岩的破坏而消失。其中部分用于岩石内结晶晶格错位,部分产生热量,还有一部分会引起岩体的震动并以地震波的形式传播出去。定义这种伴随软弱异性体围岩破坏而引发岩体震动,并以地震波的形式传播出去的能量为震源能We,其数学表达式为
We[Px,y,z(t)]=β(Uemax-Uep)
(5)
其中,We为震源能,106J;β为震动能因子,0<β<1;Px,y,z(t)为以软弱异性体为中心形成的整个空间闭区域岩体受到3个方向的主应力;We为一个以Px,y,z(t)为自变量的复合函数。
1.3 基于能量分析模型的数值分析
板块构造学说的提出,合理解释了地壳运动相对剧烈的板块边界附近是地震活动的频发区域[28]:由于板块之间的相互运动,必然造成板块岩体应力的变化,通过“世界应力图”发现全球大部分地区的最大水平主应力方向与板块绝对运动迹线保持较好的一致性,反映出构造应力与板块运动的关系密切[29];被人们称之为“世界屋脊”的青藏高原是印度板块与欧亚板块间陆陆碰撞的结果,如今印度次大陆仍向北运动,使得青藏高原受南北向巨大挤压应力场作用,表现为强烈挤压冲断,大规模的走滑与剪切、正断与拉伸等构造特征[30];有“地球上的伤疤”之称的东非大裂谷是由于非洲板块SW向运动和印度洋板块NE向运动拉伸张裂形成的,地壳下面的地幔物质上升分流,产生巨大的张力,正是在这种张力的作用之下,地壳发生大断裂,从而形成裂谷[31];总之,板块运动会产生巨大的压力与张力(构造应力场变化),其应力方向与最大水平主应力方向趋于一致,由于地壳局部区域较强的刚性,致使弹性应变能积累,当这个应变能积累到超过局部岩体强度极限时势必产生塑性破坏,并伴随能量释放。
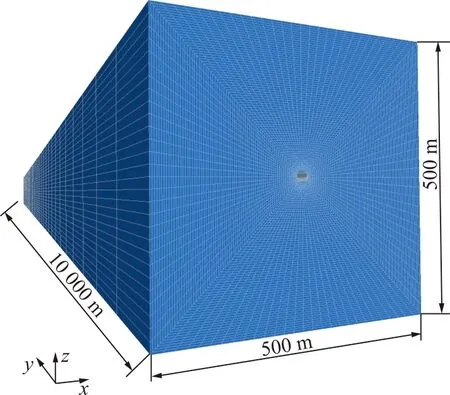
图3 含软弱异性体围岩体模型Fig.3 Model of the rocks surrounding a soft anisotropic body
数值模拟方法是近似直观反演地震发生物理过程的有效手段之一,本文应用FLAC3D数值模拟构造应力场变化产生局部塑性破坏,伴随能量释放的变化过程。构建以软弱异性体为中心的围岩体数值模型,如图3所示。基于圣维南原理[32],在小边界上进行面力的静力等效变换后,只影响附近局部区域的应力,对绝大部分弹性体区域的应力没有明显影响。因此假设软弱异性体(充斥着各种气态物质的圆形孔洞构造)为规则的圆形,半径为10 m,长度为10 km,位于地下深处10 km,取软弱异性体周围500 m半径区域范围内的岩体为均质变质岩或火成岩(参考了花岗岩的力学参数取值),具体岩石力学参数见表1。模型x轴、y轴边界水平位移与z轴上下边界垂直位移均固定。

表1 均质岩体物理力学参数Table 1 Physical and mechanical parameters of homogeneous rock masses
设软弱异性体及其周围岩体处于相对稳定的等压应力状态下,即Px(t)=Py(t)=Pz(t)=270 MPa,区域围压均为时间t的函数;结合弹塑性力学平面应变问题解法,假设垂直向主应力为软弱异性体上覆岩层自重,即Pz(t)=270 MPa,则水平向区域主应力Px(t)为惟一自变量。
1.3.1软弱异性体周围蕴含能量的变化规律
为了揭示软弱异性体周围蕴含能量的变化规律,建立起区域水平主应力与震源能、里氏震级间的对应关系,如图4所示,软弱异性体周围蕴含能量可以通过式(5)(这里β取1)定量计算得出。以区域水平主应力为自变量,震源能与里氏震级作为因变量表现出几乎一致的特征:随着水平主应力Px的改变(以Px=Pz=270 MPa为中心,曲线左侧水平主应力减小,右侧主应力增大),震源能与地震震级在曲线的两侧出现了近似指数型增长的变化规律。软弱异性体周围积聚的能量最大可达1.80×1016J,如果这部分能量一下释放,则相当于里氏7.6级地震。以软弱异性体及其周围岩体的等压状态为中心,随着水平主应力Px逐渐增加,使得整个岩体系统的总能量增加,所以软弱异性体周围岩体的能量也增大,可能引发地震的级别也越大;然而图4左侧函数变化关系显示:随着水平主应力Px的减小,系统能量总体减小的情况下软弱异性体周围岩体的能量反而增大,对应地震的级别也是越来越大。正是这种随着系统总能量的减小地震级别越来越高的反常现象,很好的解释了受构造应力作用强烈的区域附近往往是地震多发带的自然规律,即构造地应力场的剧烈变化,导致地球内部岩体突然的破裂,从而引发不同级别的地震;于是,以等压力状态为中心,将水平主应力减小软弱异性体周围岩体弹性能增长的区域划分为张拉破坏区TFZ,水平主应力增加能量增加的区域划分为挤压区CFZ(图4)。依据软弱异性体周围岩体塑性破坏形态的变化特征(图5,6),将挤压应力区地震活动分为3个阶段(图4):I为软弱异性体周围岩体塑性区为圆形;II为蝶形塑性区形成初期;III为蝶形塑性区发展末期(张拉应力区具有同样特征,本文仅以挤压应力区能量变化特征为例进行分析)。

图4 软弱异性体蕴含震源能、里氏震级与水平主应力关系Fig.4 Relationship between SEP-SS in rock masses surrounding the anisotropic body,Richter magnitude,and the horizontal principal stress
1.3.2软弱异性体围岩能量的分布特征
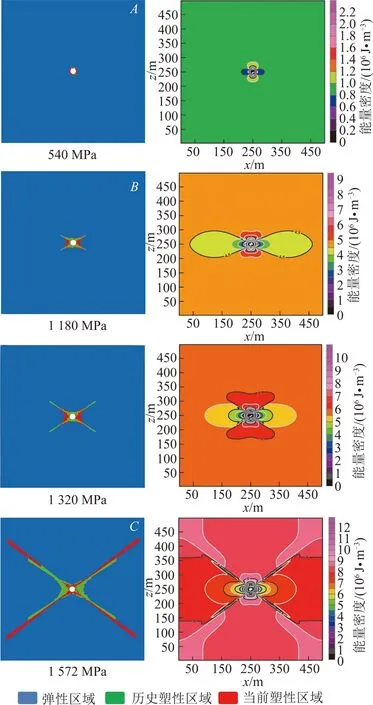
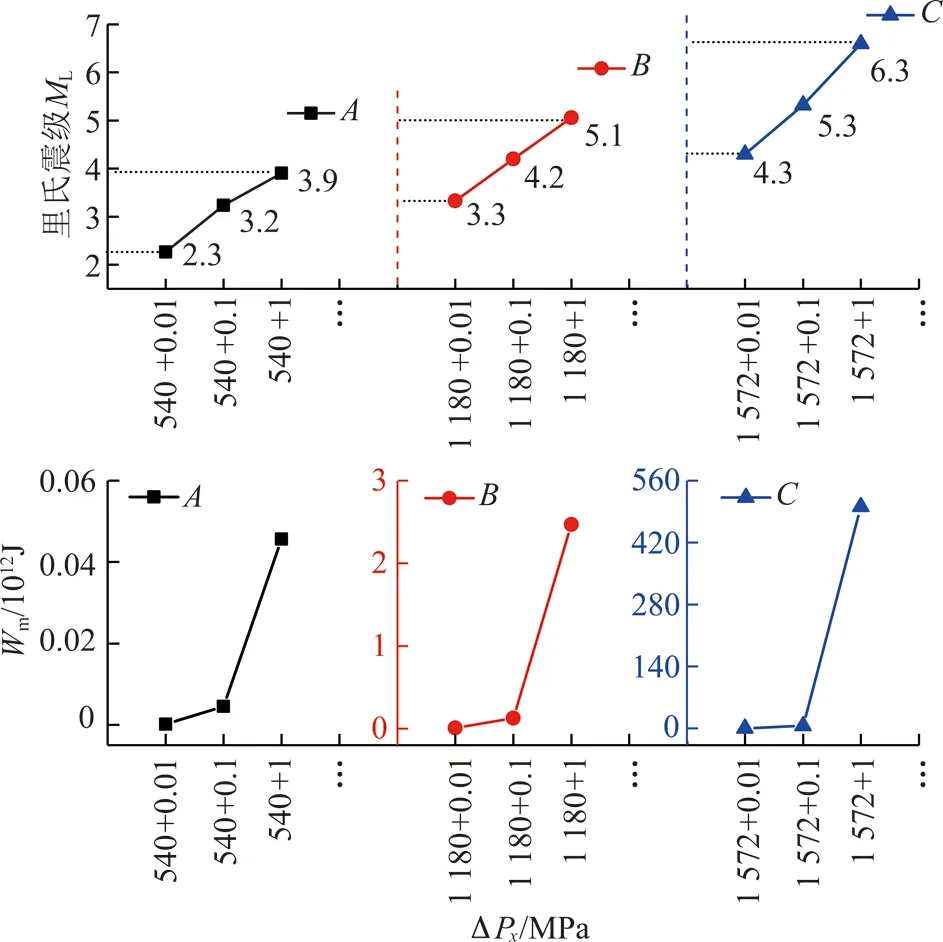
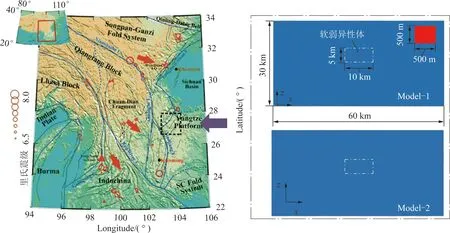
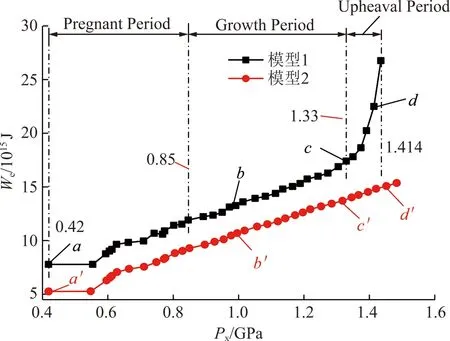
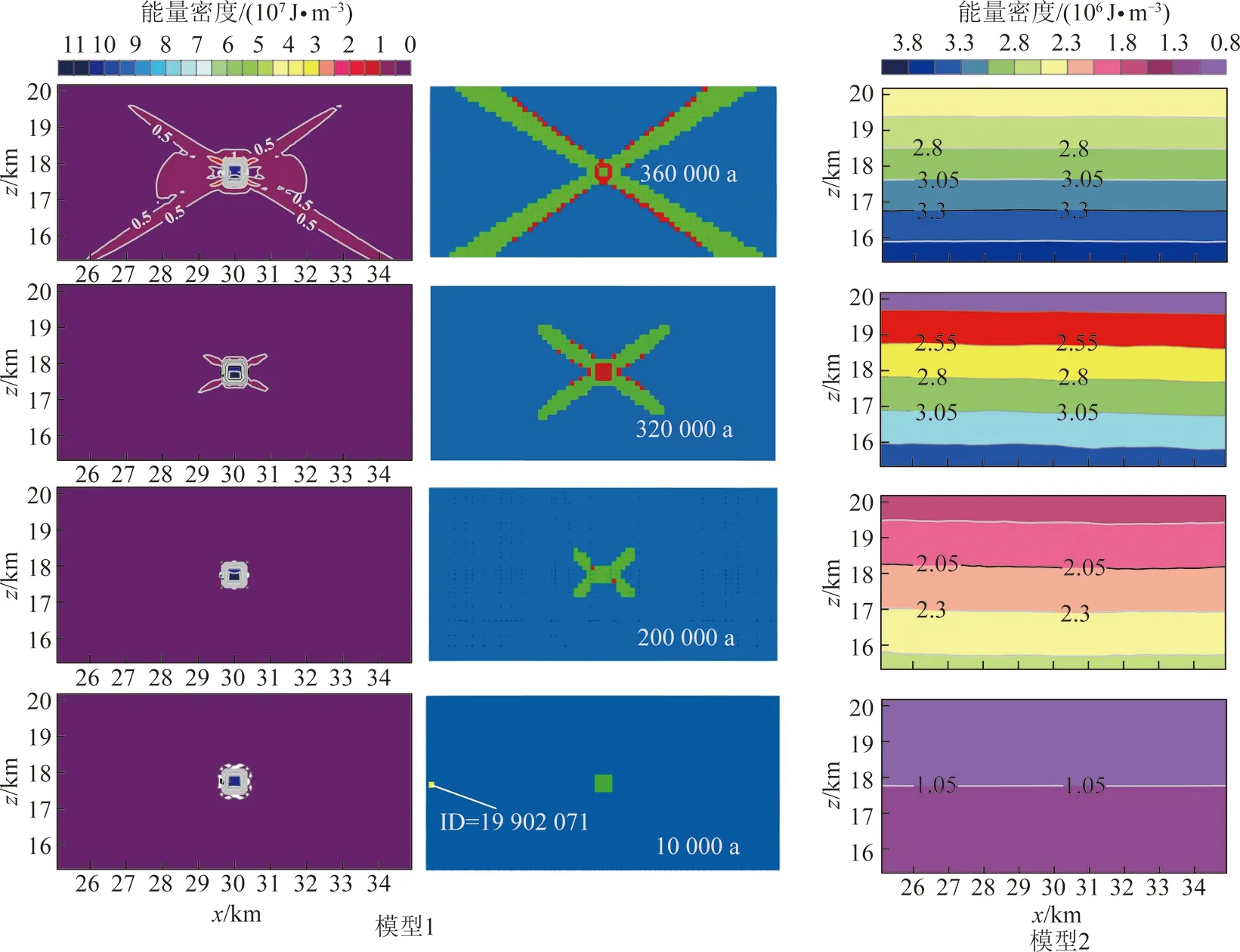
图5,6提取出不同区域主应力Px作用下,塑性破坏区形态变化与对应震源能密度分布特征。图6中A,B,C分别对应图4划分的阶段(I,II,III)中任意取得的3个特征点。分析可得软弱异性体围岩形成的蝶形破坏区周围集中了大量的弹性能,是地震发生时能量的主要来源。以挤压应力区为例,原岩应力Px=270 MPa,塑性区的形状为圆形。地质构造剧烈变化,水平应力开始增加,当Px=810 MPa时(Px/Pz=3),软弱异性体周围的破坏产生质的转变,呈蝶形变化特征。也就是说,满足条件270 MPa 图5 张拉破坏区的蝶形的演化过程与能量分布Fig.5 Evolutionary process and energy distribution of butterfly failure in TFZ 图6 挤压破坏区的蝶形的演化过程与能量分布Fig.6 Evolutionary process and energy distribution of butterfly failure in CFZ (1)地震能与震源能的关系 依据前文定义:震源能是指某种破坏状态下软弱异性体周围岩体内的集中能量,是某一时刻的状态量值,与时间无关。而真实地震发生时记录到的以地震波形成释放的能量是以时间为周期加以衡量,例如里氏震级(ML)、面波震级(Ms)及体波震级(Mb,MB分别为用1 s和5 s左右的地震体波振幅来量度地震的大小)中能量的计算都是以波的周期长度作为时间单位。为了方便起见,本文定义单位时间释放的震源能为地震能Wm,如图2(b)所示。结合式(5)构建地震能Wm与震源能We的关系: Wm=We[Px,y,z(t+Δt)]-We[Px,y,z(t)]= We(Px,y,z+ΔPx,y,z)-We(Px,y,z) (6) 式中,Wm为地震能,即地震发生时每秒释放的震源能,J/s;t为时间变量,s;Px,y,z(t)为地震发生前时间t的区域主应力,MPa;Px,y,z(t+Δt)为地震发生时的区域主应力,MPa;ΔPx,y,z为经历Δt时刻的区域主应力增量,MPa/s;D为常量;R为全体实数域。 式(6)表明,对于软弱异性体而言,发生地震时的震级和释放的能量仅取决于区域主应力Px,y,z(t)及其增量ΔPx,y,z。 (2)区域主应力微小变化触发地震的可能性分析 与地球提供给板块运动的能量相比,地震所释放的能量仅仅占很小的部分[33];地球板块运动仿佛一直处在不稳定的边缘,而地震似乎可以看成是围绕这一“临界状态”的“涨落”[34]。固体潮汐应力、地球自由震荡、已有断层的突然破裂、采矿活动等微小应力亦可“触发”大级别地震的自然现象不断被发现,甚至极其微小的远处大地震的面波通过(引起的水平张应力仅为0.025 MPa)也能引发地震[35-39]。由此看来,“触发”地震似乎无需非常大的应力变化,这一说法令人难以置信。 这种微小应力变化“触发”地震的自然现象可通过式(6)的计算结果很好的定量解释。假设软弱异性体位于挤压构造应力场中,则在受到1,0.1与0.01 MPa/s的触发应力作用时,不同震前状态(图4,A点540 MPa;B点1 180 MPa;C点1 572 MPa)下的地震能和震级如图7所示,受到相同触发应力增量作用时,围岩塑性破坏形态呈圆形与蝶形塑性破坏形成初期(特征点A+B)的地震能和地震级较小,蝶形塑性破坏发展末期(特征点C)最大,震级可达6.6级。此时,水平主应力仅增加0.01 MPa/s,即可触发里氏4.3级左右地震,说明地震诱因存在着“压倒骆驼的最后一根稻草”现象;处于蝶形塑性破坏急剧扩展阶段,地震对地应力分布具有敏感依赖性,区域主应力的任何微小增量ΔPx,y,z都有可能引发能量系统的灾变,可以推测微小、甚至极微小的应力变化都可“触发”较大级别的地震。这里需要指出:① 由于应力是矢量,以上表述的触发应力方向是与区域水平主应力的方向保持一致的。如果二者的作用方向不一致,其结果也会完全不一样,尤其当触发应力和区域水平主应力的作用方向完全相反时,即使再大的应力变化也不会“触发”地震;② 区域主应力(x,y,z方向上)尽管有时存在相互作用关系,但它们之间也可看成独立的自变量,即以上所有过程基于固定区域垂直主应力,仅分析水平主应力变化引发地震的自然现象,也可用于解释不同方向上区域主应力变化引起的地震能量改变。 图7 应力增量对应能量与震级变化Fig.7 Changes in energies and magnitudes corresponding to different stress increments 自然界中的软弱异性体形形色色,有各种类型。软弱异性体极少是圆的,存在各种各样的形状;软弱异性体很多情况下会是被坚硬岩体包围着的局部相对软弱的地质软弱构造。 中国大陆西南地区是印度板块与欧亚板块碰撞形成的“挤出构造”,地处南北地震带中南部的川滇菱形构造块体及其边缘区域,构造应力环境极其复杂。研究区域具体的空间位置为:26°~28°N,103°~104°E,其中包含了鲁甸6.5级(2014年中国云南省)地震震中所在位置。考虑到鲁甸震源区地壳厚度变化较大,从44.5 km增加到59.0 km的特点[40],采用基于拉格朗日连续介质法的FLAC3D5.0数值模拟软件[41],构建了真实地壳的三维有限差分模型,如图8所示,东西向为模型的走向,其长度为60 km,高度取为30 km,厚度为100 m(南北向表示厚度方向)。为了方便模型的构建和突出所研究的中心区域,建模中进行了必要的简化,由于本文主要研究地震震源能量来源,对于震中地表及走向范围内的地势差异影响未作考虑;由于模型所建高度未达到岩石圈底部Moho面,故真实岩石圈底部的起伏变化也加以忽略。在距模型地表12 km深度处设置一软弱异性体(长方体单元)(图8),其尺寸为500 m×500 m×100 m(x×z×y)。 模型岩石力学参数选取:依据摩尔-库仑破坏准则,涉及弹塑性介质的5个物理力学参数分别为:弹性模量E、泊松比μ、黏聚力c、内摩擦角φ和抗拉强度σc。由PREM地球模型得出地震P波、S波在地球内部传播速度变化特征:随深度增加,地震波波速增加,岩石更加致密,地壳岩体的弹性模量也同等增加。在30 km深度中国大陆西南地区的平均S波波速约为3.74 km/s[43],平均P波波速为6.45 km/s[44-45],随深度变化的密度取值在2.35~2.85 g/cm3内呈梯度增长[46]。于是,E与μ依据式(7)可求出[47],即 (7) 式中,α与β分别为P波和S波的传播速度,km/s;ρ为已知岩体的密度,kg/m3。 将计算所得弹性模量按梯度均匀赋值于模型,同时参照花岗岩的岩石力学性质[48],确定未给出的物理力学参数,具体取值见表2(软弱异性体参照煤的物理力学参数取值)。 为了方便对比分析,将已构建的含软弱异性体模型定义为模型1。同时建立无软弱异性体模型2,具体参数取值参照表2。用六面体单元对2个模型进行网格划分,对于模型1进行局部网格加密处理,单元总数为246 800个,节点总数为274 349个。 图8 西南地区构造简图[42]Fig.8 Geological structures of southwest China[42] 表2 模型物理力学参数Table 2 Physical and mechanical parameters of the model 板块运动观测网络给出了中国大陆地区地表GPS速度场结果,模型所在区域(图8)内部鲁甸地震临近地区的GPS监测资料真实反映了包谷垴—小河断裂带(1991—2013)东西两侧运动存在明显差异,即西侧运动量值约为10 mm/a左右,东侧为6 mm/a[49-50]。本文所建模型的左侧边界相对于右侧可以移动,移动速度取2个边界实际移动速度的差值,并将该相对速度值插值于模型左侧边界面,作为水平向板块运动位移移进量,且假定从地表到30 km深度保持一致[51-52],速度取值为4 mm/a(每年4 mm),在FLAC3D数值模拟软件中表现为1 a(年)相当于1个step;垂直方向位移保持自由;右侧界面水平向固定,等同于板块运动相对静止的边界面,其他方向自由;上表面为自由边界,即法向应力和剪应力均为0,对于底部边界,将底面垂直方向位移约束为0,而水平方向自由,具体如图9所示。整个模型范围内岩体初始应力环境设定为自重应力场,铅直应力变化随深度成正比递增,由此构建了模型1与模型2的初始应力环境。 图9 约束条件与初始位移速度加载模型Fig.9 Constraint conditions and loading model for initial displacement speed 2.3.1在有无软弱异性体条件下,地震震源能变化规律的对比分析 软弱异性体总体积只占整个地壳模型总体积的14‰,为了便于分析软弱异性体周围岩体能量的分布规律,选取以上两数值模型单元体ID=19 902 071的区域水平应力为自变量,10 000 m×5 000 m×100 m(x×z×y)内(图8)蕴含能量值为因变量绘制曲线图,具体如图10所示,能量值由式(5)计算得出。在初始自重应力场影响下,随着模型边界位移移进量逐渐增加,该区域水平应力Px(t)逐渐增大,与因变量震源能We呈正指数型增长关系;当区域水平应力达到某一极限值Pxmax=1.414 GPa时,软弱异性体集中能量具体量值可达2.25×1016J。为了对比分析相同力学条件下无软弱体围岩能量分布特征,建立数值分析模型2。显然,无软弱异性体模型2集中震源能We与区域水平主应力之间呈线性增长关系;考虑塑性区形态的变化特征与积聚能量的分布特征,将能量变化曲线分为3个阶段:蝶形塑性破坏还未形成0~150 000 a(仅软弱异性体围岩发生塑性破坏)、蝶形塑性破坏形成初期150 000~320 000 a(蝶形塑性破坏形成,并稳速扩展)与蝶形塑性破坏扩展末期320 000~370 000 a(蝶形塑性破坏急速扩展)。 2.3.2不同应力状态下震源能的分布特征分析 从图10划分的3个阶段中任意选取特征点a,b,c,d和a′,b′,c′,d′,绘制塑性区形态与集中能量分布对比图11。由该图可知,模型1积聚震源能总体分布特征表现为软弱异性体中心集中能量最多,并由里向外逐级减弱,尤其随着蝶形塑性区的发展,软弱异性体围岩会形成蝶形能量集中区(图11中32万a首次生成),蝶叶周围岩体也积聚大量弹性能;无软弱异性体模型2能量呈层状分布,其积聚能量分布与线性递增的曲线能量值呈正相关,符合客观规律。 图10 塑性破坏区与震源能分布Fig.10 Distribution of plastic damage zones and seismic source’s energy 图11 特征点集中能量分布对比Fig.11 Comparison of distributions of energies accumulated at feature points 以上对比分析证实:构造应力主导下的真实地壳岩体,由于软弱异性体的存在造成了其周围岩体的能量集中,随着围岩蝶形破坏的发展能量逐渐呈蝶形分布特征,且随着蝶叶的扩展其周围岩体持续破坏并伴随能量释放,发生一系列地震。 Pregnant Period:蝶形塑性破坏还未形成时期;Growth Period:蝶形塑性破坏形成初期;Upheaval Period:蝶形塑性破坏扩展末期。 2.3.3不同围岩塑性区状态下地震的触发 选取模型1中不同塑性区状态下(a,b,c三点)集中震源能为初始值,取微小应力增量ΔP=0.001 MPa,则地震能对应里氏震级变化关系见表3,地震能由式(6)定量计算得到。处于蝶形塑性区形成初期与稳速发展时期,微小应力可能触发里氏2.3和2.5级地震,急速扩展末期的蝶形塑性区微小应力会引起碟叶发生急剧扩展,此时释放地震能可达6.02×1010J,相当于里氏4.0级地震,说明地震发生时,真实地壳围岩系统对于软弱异性体周围塑性区状态具有敏感依赖性,蝶形塑性区一旦出现,系统由稳态向非稳态能量积聚转变,处于剧变期的围岩系统本身积聚震源能量值已经很大,任何微小的扰动即可引发能量释放,蝶形塑性破坏发生灾变产生大级别地震。 表3 微小力触发地震能与震级变化关系Table 3 Relationship of seismic energies triggered by microstress and corresponding magnitudes (1)得到了一种计算地震震源围岩能量的方法,发现了地震震源能、相应里氏震级与水平主应力关系曲线呈指数型变化规律,即以等压状态为中心,随着水平主应力减小(形成张拉破坏区),震源能与对应震级呈负指数型增长;随着水平主应力增大(形成挤压破坏区),震源能与对应震级呈正指数型增长,且蝶形破坏围岩形成了以软弱异性体为中心的蝶形能量集中区,蝶叶周围岩体集中了大量的弹性能。 (2)揭示地震能量来源的力学本质。由于地壳内部软弱异性体的存在,使得周围岩体应力重新分布,形成围绕软弱异性体的应力集中。应力的改变也带来了软弱异性体周围岩体能量的集中,由于构造应力场变化而产生的巨大压力与张力,造成软弱异性体周围岩体出现蝶形破坏,积聚的弹性能得以释放,形成以软弱异性体围岩蝶形破坏区为震源的地震。也就是说,地震的能量主要来源于软弱异性体周围岩体内的能量集中,并以此构建了地震能量的分析模型。 (3)应用数值分析方法初步论证了微小应力扰动可以引发大级别自然地震的观点。实际上不同的应力变化可引发不同级别的地震,之所以同等应力变化下地震释放的能量大小存在巨大差别,是由地震发生时塑性破坏范围与围岩积聚能量所处的状态决定的。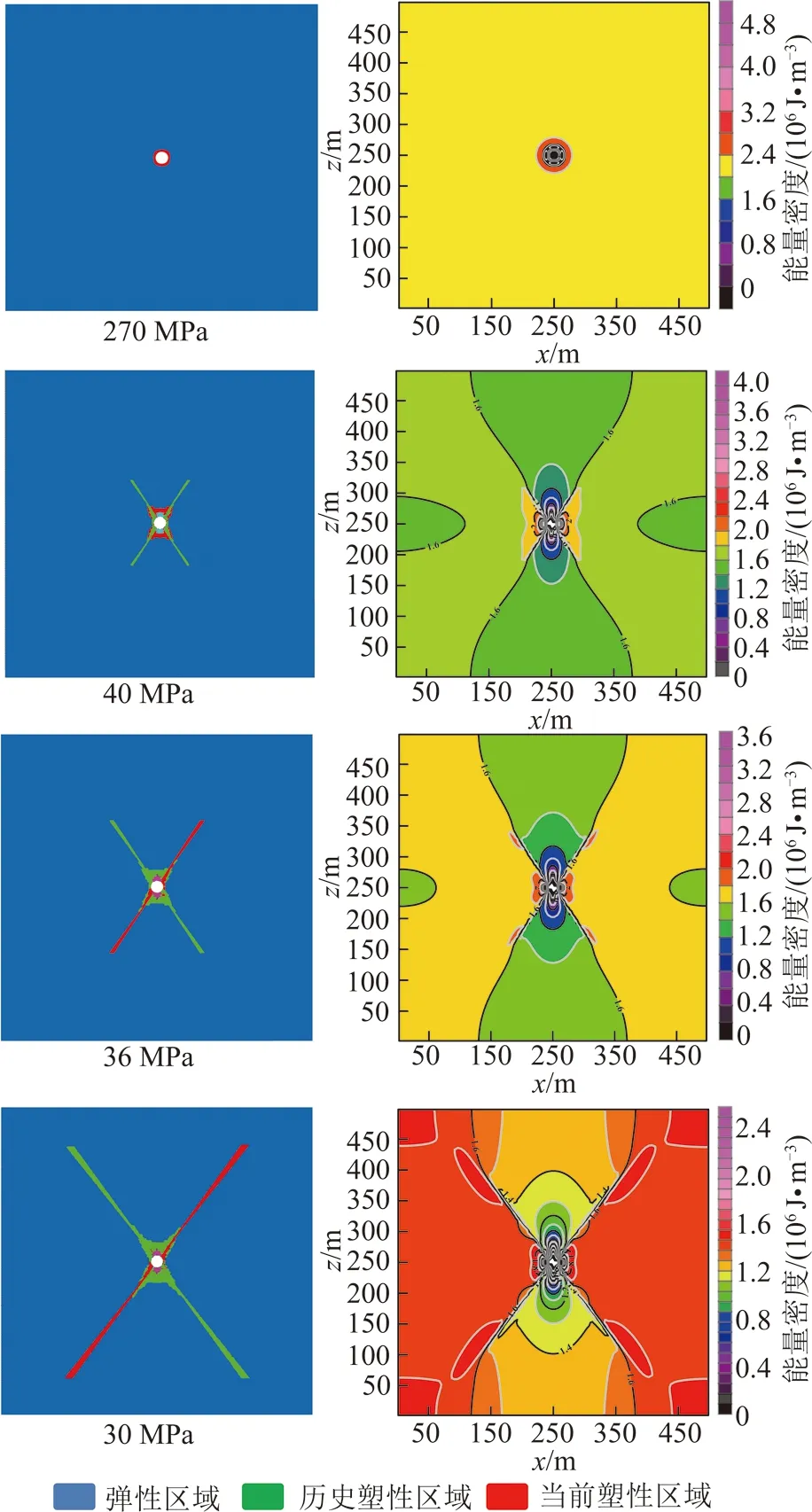
1.3.3 自然地震的触发
2 震例分析
2.1 区域构造背景及有限差分模型

2.2 边界条件与初始条件

2.3 数值模拟结果分析

4 结 论
——以淮南矿区为例

