随机介质中的探地雷达叠前逆时偏移成像
王敏玲, 龚俊波, 王洪华, 罗崇炎
(1. 桂林理工大学 地球科学学院,桂林 541004;2. 广西隐伏金属矿产勘查重点实验室,桂林 541004)
0 引言
探地雷达(Ground Penetrating Radar, GPR)是利用高频脉冲电磁波来探测地下地质体结构及物性参数的一种重要浅部地球物理方法[1],具有无损性、高分辨率、高效率等特点,在工程勘查、环境监测、考古调查等领域中得到广泛应用[2-6]。逆时偏移成像[7]作为一种将实测雷达数据与真实地质结构转换的关键技术,一直以来是GPR研究的重点,通过逆时偏移成像可获得地下精细结构分布,提高解译精度[8]。
对GPR逆时偏移成像的研究,国内、外学者已经开展过相关工作。底青云[9]考虑地下介质电导率对GPR信号的衰减,开展了衰减介质GPR逆时偏移成像研究;鲁兴林和钱荣毅[10]通过数值算例分析了逆时偏移与克希霍夫偏移的优缺点,得出了逆时偏移成像精度更高、效果更好的结论;Fu等[11]通过对传统逆时偏移成像剖面进行去模糊滤波处理,有效提高了逆时偏移的成像精度;Liu等[12]提出了一种基于分层介质格林函数的频率域GPR逆时偏移算法,提高了计算效率;王敏玲等[13]将激发振幅成像条件运用于GPR逆时偏移成像中,有效提高了逆时偏移计算效率;Bradford等[14]为克服地形起伏对成像精度的影响,提出了一种适用于起伏地表的GPR逆时偏移算法,数值算例表明:该算法比传统高程静校正偏移方法的成像精度更好。
上述GPR逆时偏移成像研究大都将偏移速度模型看作均匀、分块介质模型,侧重于理论数据的逆时偏移成像研究。然而实际地下介质是随机分布的,电磁波在其中传播时会产生大量的不相干扰动,其实质是源于介质在小尺度上的非均匀性[15]。采用确定性的均匀介质模型难以描述小尺度上的非均匀、随机分布特性。因此,如何真实描述地下介质的小尺度非均匀特性,成为当前GPR研究的热点。随机介质模型建立理论是将地下介质的小尺度非均匀性性视为一种随机过程,采用统计学方法加以描述介质小尺度上的非均匀分布特征[16]。戴前伟等[17]采用随机过程中的谱分解理论和椭圆自相关函数构建随机介质GPR模型,并利用无单元法分析电磁信号在随机介质的传播特征;宋二乔等[18]利用时域有限差分法模拟了雷达波在季节性冻土随机介质中的传播特征;郭士礼等[19]采用多相随机介质模型建立方法构建了混凝土随机分布结构,并分析了GPR信号的随机扰动特征与多相离散随机介质模型参数之间的关系。笔者在上述理论研究基础上,采用随机过程中的谱分解理论和椭圆自相关函数构建了2个典型的GPR随机介质模型,并采用时域有限差分法(Finite Difference Time Domain, FDTD)正演模拟和逆时偏移成像,分析了随机介质中的电磁波传播特征和异常体的逆时偏移成像效果,为可否利用GPR方法实现地质结构的高精度探测提供理论参考。
1 随机介质GPR模型建立方法
随机介质模型主要由非均匀性大、小两种尺度组成。大尺度非均匀性描述介质的背景特性,小尺度非均匀性是加载在大尺度上的一种随机扰动,通常用一个均值为零的二阶平稳随机过程来表示[16]。GPR探测过程中,电磁波在地下介质中传播时主要受介质相对介电常数的影响。二维随机介质中空间坐标(x,z)处的相对介电常数ε(x,z)可表示为:
ε(x,z)=ε0(x,z)+δε(x,z)
(1)
其中:ε0(x,z)为背景介质(大尺度)的相对介电常数;δε(x,z)为背景介质上的空间相对随机扰动量(小尺度)可表示为:
φ(x,z)=δε(x,z)/ε0
(2)
假设φ是具有零均值、一定方差及自相关函数的空间平稳随机过程[16],则φ满足[17]:
〈φ(x,z)〉=0
(3)
〈φ2(x,z)〉=α2
(4)
构造二阶平稳过程ε(x,z)的步骤如下[16, 20]:
1) 选择自相关函数。目前,描述随机介质的自相关函数有多种。其中,混合型自相关函数能较好地描述具有多尺度平滑的随机介质而在弹性波、电磁波正演模拟领域得到广泛应用,其表达式为:
(5)
式中:a,b分别是介质在x,z方向上的自相关长度,是表示相似程度大小的参数;p为粗糙度因子。
2) 计算混合型自相关函数φ(x,z)的二维傅里叶变换φ(kx,kz)。
3) 用随机数发生器生成0~2π之间服从独立均值分布的二维随机场φ(kx,kz)。
4) 计算随机功率谱函数ψ(kx,kz),其表达式为:
exp[iθ(kx,kz)]
(6)
式中,ω(kx,kz)为窗函数,通过窗函数的应用可降低空间离散误差,从而减少自相关函数的低频能量[17]。
5) 计算ψ(kx,kz)的二维傅里叶逆变换,从而得到随机扰动v(x,z)。
6) 计算随机扰动v(x,z)的均值和方差:
μ=〈v(x,z)〉
(7)
d2=〈[v(x,z)-μ]2〉
(8)
7) 通过规范化生成均值为零、方差为α2的随机扰动:
(9)
图1为按照上述理论,构建的不同自相关长度随机相对介电常数模型。其中,背景介质的相对介电常数为3,其随机扰动量的方差为0.1。由图1可知:随机介质中的相对介电常数呈随机分布,局部区域存在微小异常;自相关长度a,b分别表示随机介质在x,z方向上扰动的平均尺度,自相关长度越大,则该方向上相对介电常数的连续性越好;当a=∞,表示在x方向均匀分布,此时二维随机介质变成一维层状随机介质,如图1(d)所示。由此可见,笔者采用的随机介质建立方法能灵活、有效地描述地下实际介质的非均匀随机分布特性。
2 GPR逆时偏移成像方法
GPR逆时偏移[21]主要包括以下三个过程:源点电磁波场的正向传播,接收点电磁波场的逆时外推和成像条件的应用。前两个过程的实现可利用相同的数值模拟方法,如FDTD[22]、时域有限单元法[23]、时域伪谱法[24]等,其中FDTD具有原理简单、计算效率高、易实现等优点而在GPR数值模拟中得到广泛应用。因此,我们采用FDTD计算源点正传电磁波场和接收点反传电磁波场。
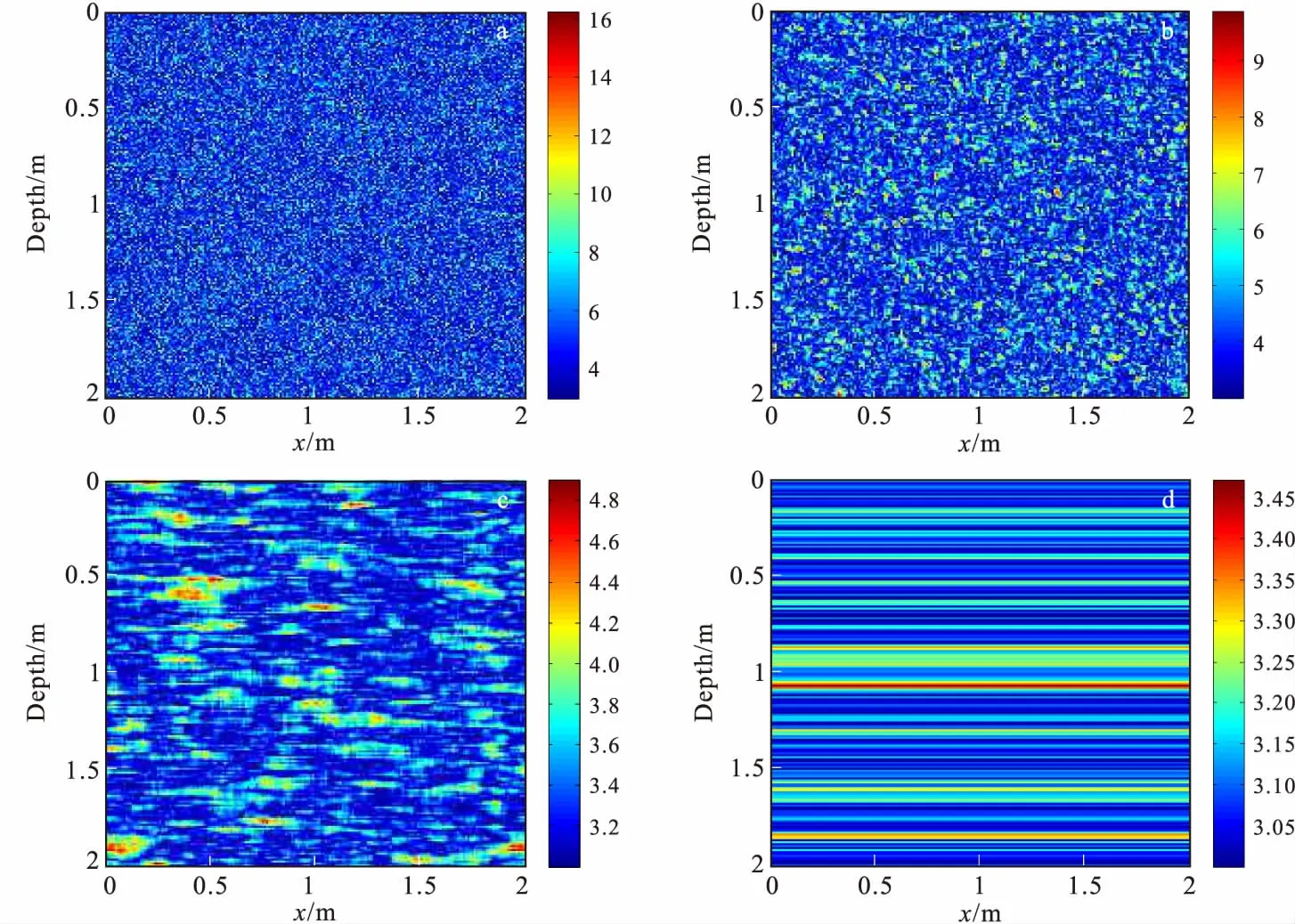
图1 不同相对常数的椭圆自相关函数产生的随机介质相对介电常数模型Fig.1 Random media models of relative dielectric permittivity in different auto-correlation length media produced with intermixed ellipsoidal autocorrelation function(a)a=1,b=1;(b)a=10,b=10;(c)a=100,b=20;(d)a=∞,b=20
成像条件的应用是影响逆时偏移成像效果的另一个重要因素。目前,GPR逆时偏移中应用最广泛的成像条件是互相关成像条件[25]。互相关成像条件以时间一致性原理为基础,通过计算源点正传电磁波场和接收点反传电磁波场的零延时互相关,从而获得成像剖面。标准的零延迟互相关成像条件公式为:
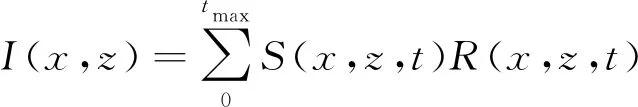
(10)

为此,Kaelin等[26]采用源点正传电磁波场或接收点反传电磁波场对零延时互相关成像条件的计算结果进行归一化,提出了归一化互相关成像条件,其表达式为:
(11)
由式(11)可知:归一化互相关成像条件不但能削弱近地表源点强振幅影响,而且可提升深部反射界面的能量。目前,归一化互相关成像条件在弹性波、声波和电磁波逆时偏移中得到广泛应用[27, 28, 21]。笔者采用该成像条件开展GPR逆时偏移计算,开发的随机介质GPR逆时偏移成像算法如图2所示。逆时偏移的第一步是给定偏移模型和激励源,利用FDTD模拟激励源在模型中传播的正传波场,计算至最大采样时间tmax;第二步是将接收点所接受到的数据借助FDTD沿时间轴进行电磁波场的逆时延拓至零时刻;第三步,把相同时刻相同位置上的电磁波场应用相关成像条件进行成像,本文用归一化互相关成像条件进行偏移成像。对单个源点进行归一化互相关成像后,需要对偏移结果进行拉普拉斯滤波去除剖面顶部的低频噪声,并将多个源点偏移结果进行叠加,获得最终的偏移结果。
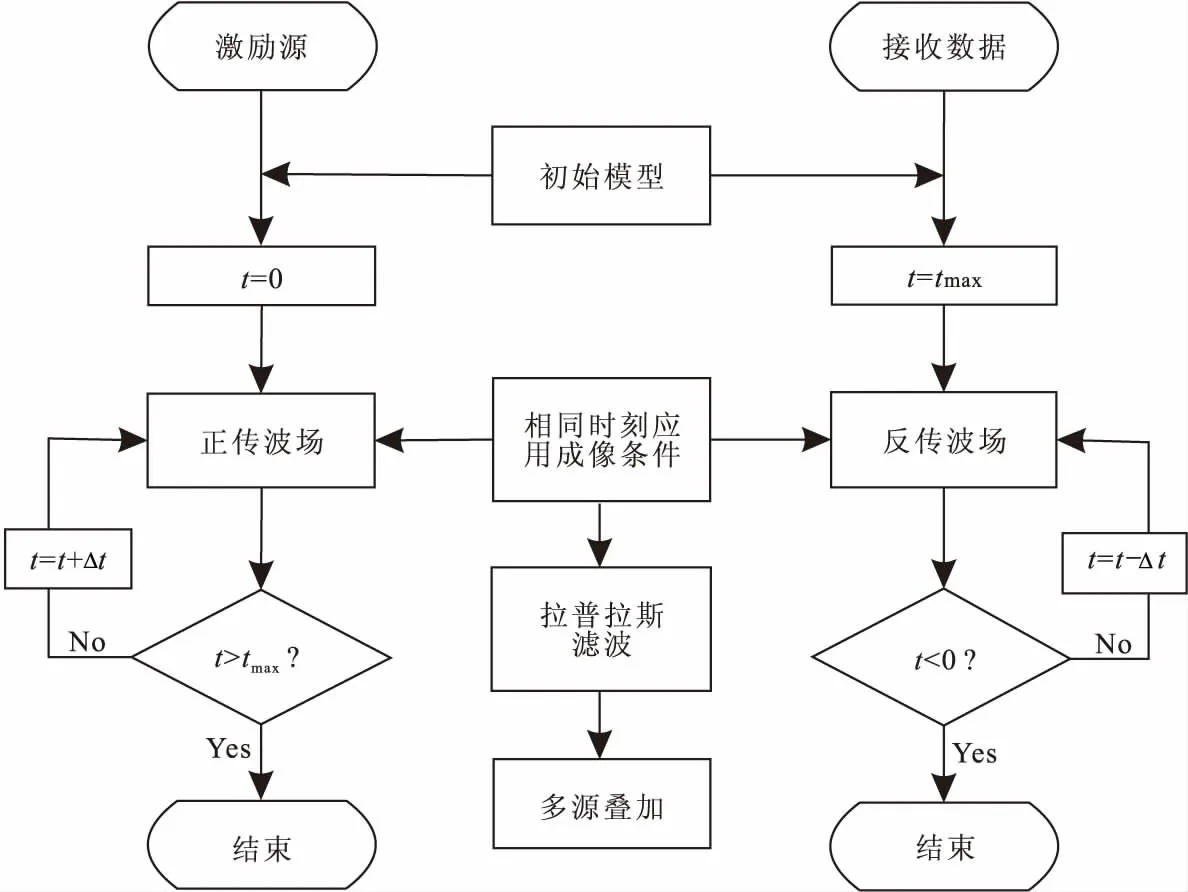
图2 随机介质GPR逆时偏移流程图Fig.2 Flow chart of prestack RTM algorithm in random media
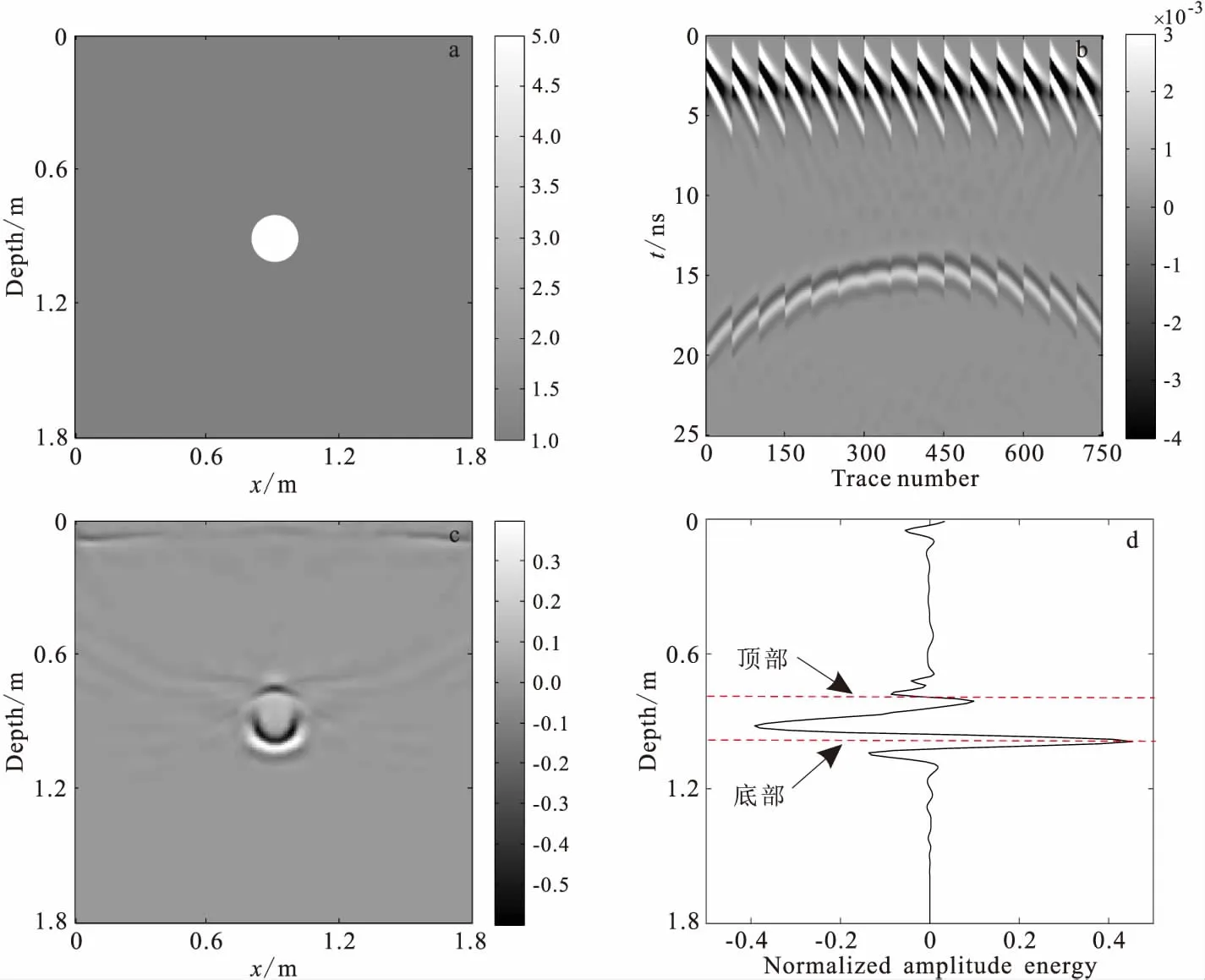
图3 圆状体GPR模型及其逆时偏移结果Fig.3 Schematic diagram of circle model and its migration reverse time result(a)圆柱体GPR模型;(b)多偏移距GPR正演剖面; (c)逆时偏移剖面;(d)单道逆时偏移结果
3 数值算例
依据上述方法原理,编制了相应的随机介质GPR叠前逆时偏移程序,利用该程序对两个典型随机介质GPR模型的多偏移距正演数据进行逆时偏移成像,并与相应背景介质的GPR模型的逆时偏移结果进行对比分析。
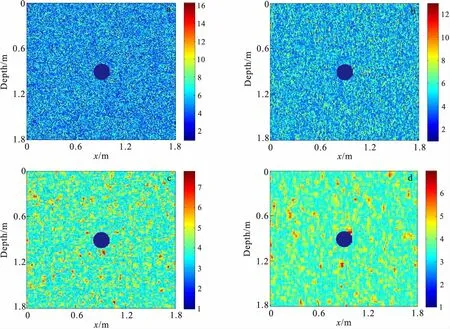
图4 不同自相关长度的随机介质圆柱体模型Fig.4 Random media circle models of relative dielectric permittivity with different auto-correlation length(a)a=1,b=1;(b)a=1,b=10; (c)a=15,b=15;(d)a=15,b=30
3.1 模型一
图3(a)是大小为1.8 m×1.8 m的圆形空洞模型示意图,模型介质的相对介电常数为5,电导率为0.001 S/m;中间埋有一个半径为0.1 m的圆形空洞,其圆心位置为(0.9 m, 0.9 m)。利用FDTD法对该模型进行多偏移距正演和逆时偏移时,发射源信号采用中心频率为500 MHz的雷克子波,采样时间间隔为0.01 ns,时窗长度为25 ns;地表布设15个发射天线,发射天线的间距为0.1 m,第一个发射天线放置在原点,其余发射天线依次往右布置;每个发射天线右侧布置50道接收天线,接收点的间距为0.01 m,水平方向上覆盖了0.5 m。图3(b)为模型一的多偏移距GPR正演剖面,由图可知:圆形空洞产生的双曲线反射波清晰可见,但不能准确定位异常体的真实空间位置。利用二维GPR逆时偏移成像算法对图3(b)中的正演数据进行逆时偏移,获得了成像剖面如图3(c)所示。偏移剖面中,绕射波能量几乎都得到收敛,反射波能量归位到空洞的真实空间位置,且空洞顶部和底部真实位置与图3(c)中水平位置0.9 m处的归一化单道波形能量位置相符,如图3(d),所示验证了本文构建的GPR逆时偏移算法的正确性和有效性。
为了更好地分析二维GPR逆时偏移成像算法对实际地下随机分布介质的成像能力,将模型一的背景介质设置为不同自相关长度的随机介质,建立的模型a、模型b、模型c、模型d,如图4所示。由图4可见,随机介质中自相关长度是影响介质非均匀尺度的重要因素,自相关长度越大,非均匀尺度越大,自相关长度越小,非均匀尺度越小,取不同的自相关长度可以很好地表示地下不同非均匀尺度的随机介质模型。
图5为利用FDTD对图4所示的随机介质模型进行多偏移距正演计算,获得GPR正演剖面。由图5可见:自相关长度a、b均为1时,圆形空洞产生的反射波清晰,如图5(a)所示;自相关长度越大,双曲线反射波能量越微弱,如图5(b)和图5(c)所示;当自相关长度a=15,b=30,如图5(d)所示,双曲线反射波形态失真,不易被识别。对比图5和图3(b)可知:电磁波在随机介质中传播时散射强烈,散射波相互叠加,形成了明显的随机扰动,致使反射波扭曲变形,不连续,不易辨识,降低了GPR回波的信噪比和分辨率。
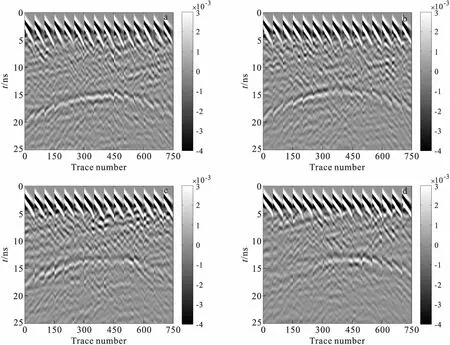
图5 图4中的随机介质GPR模型的多偏移距正演剖面Fig.5 Simulated multi-offset GPR profiles of media GPR models with different autocorrelation length as in Fig 4(a)a=1,b=1;(b)a=1,b=10; (c)a=15,b=15;(d)a=15,b=30
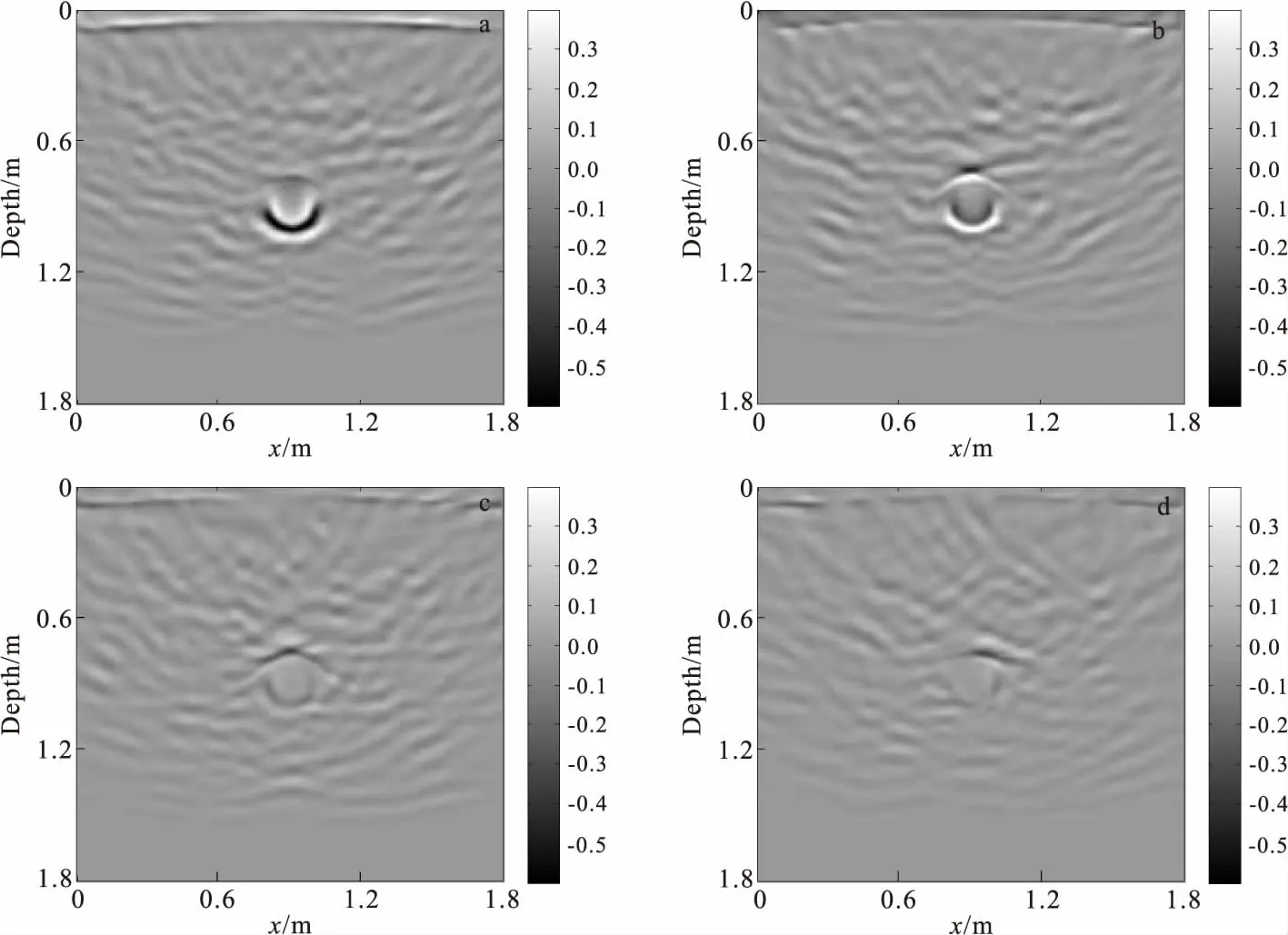
图6 利用图5中的多偏移距GPR正演数据进行逆时偏移获得的成像剖面Fig.6 Imaging results of simulated multi-offset GPR dataset by using the GPR reverse time migration of random media(a)a=1,b=1;(b)a=1,b=10; (c)a=15,b=15;(d)a=15,b=30
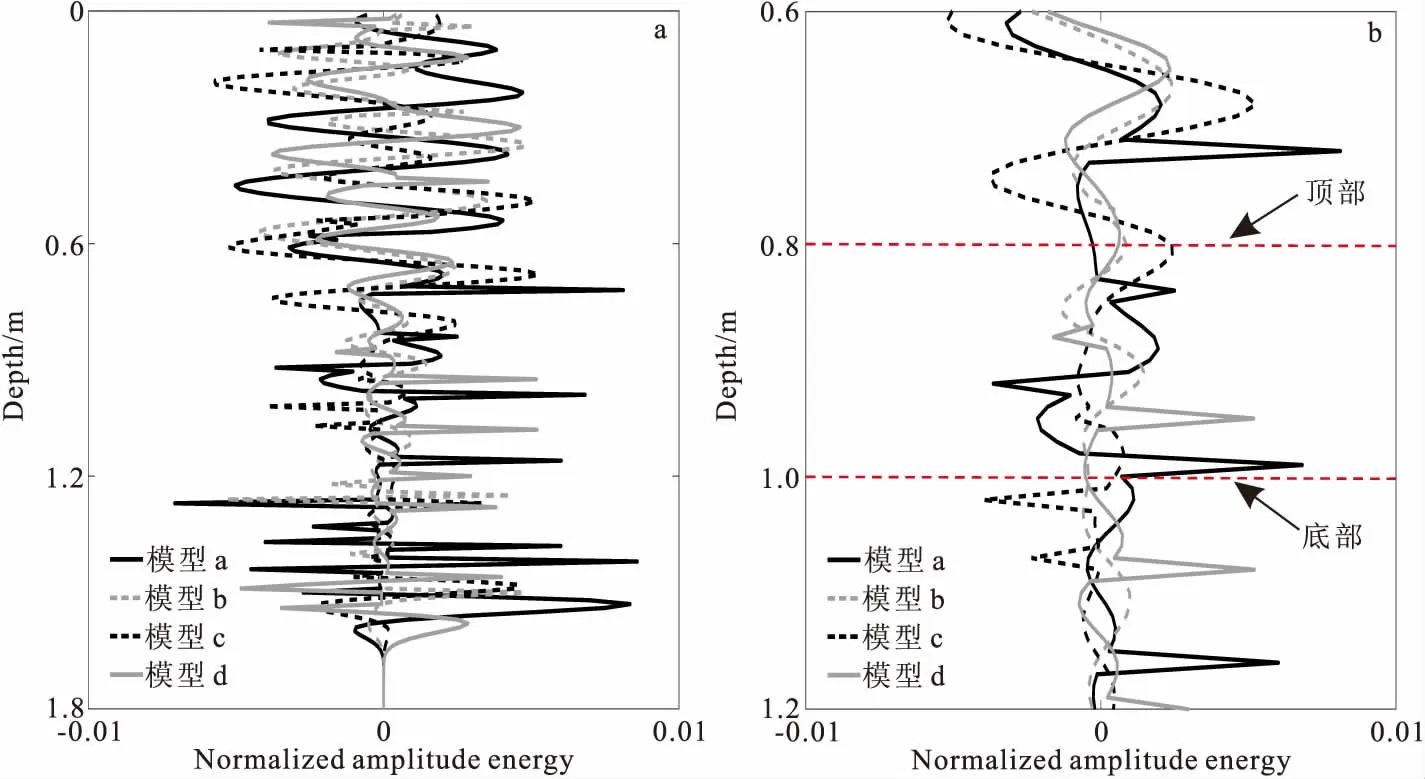
图7 图6中地表中心位置(0.9 m)处的单道波形对比Fig.7 Comparison of single waveforms extracted from the center surface position of 0.9 m in Fig 6(a)0 m~1.8 m;(b) 0.6 m~1.2 m
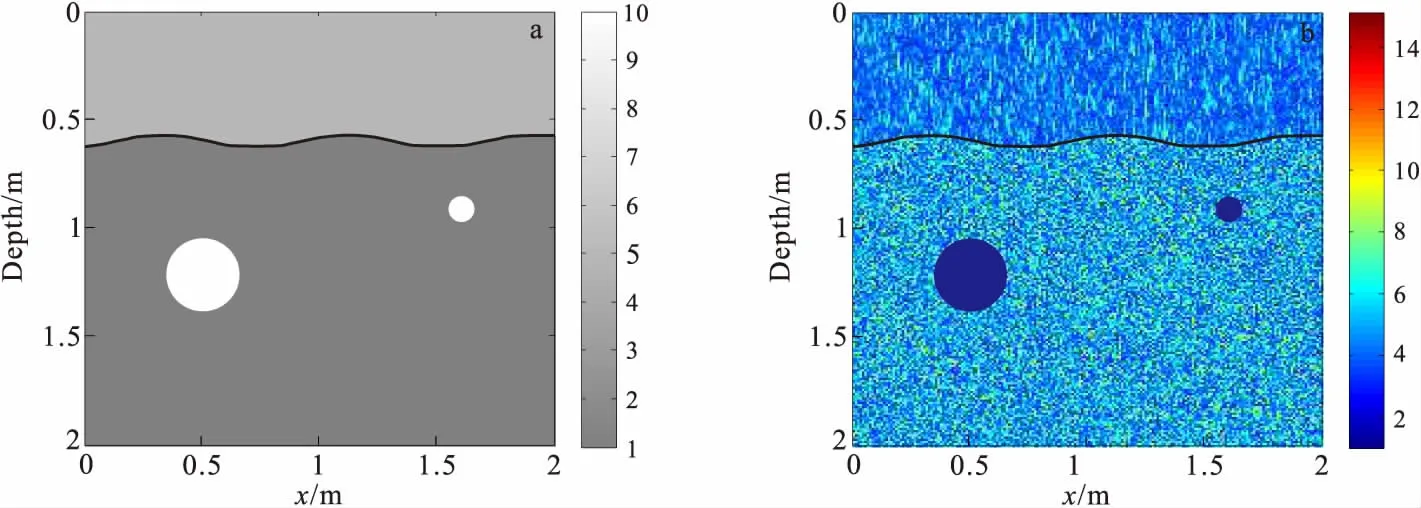
图8 复杂GPR模型二示意图Fig.8 Schematic diagram of complex GPR model(a)背景介质为均匀介质;(b)背景介质为随机介质
利用随机介质GPR叠前逆时偏移成像算法对图5中的多偏移距正演数据进行逆时偏移,获得的成像剖面如图6所示。由图可见,自相关长度越小,绕射波归位到其真实空间位置的效果越好,能量收敛越集中,圆形空洞成像越清晰;自相关长度越大,绕射波归位效果越差,圆形空洞成像越模糊;当自相关长度达到15以上时,反射波和绕射波能量几乎不能收敛,异常体的空间分布位置难以被识别。
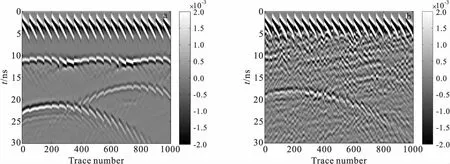
图9 复杂GPR模型二多偏移距正演剖面图Fig.9 Simulated multi-offset GPR model of complex GPR model II(a)背景介质为均匀介质;(b)背景介质为随机介质
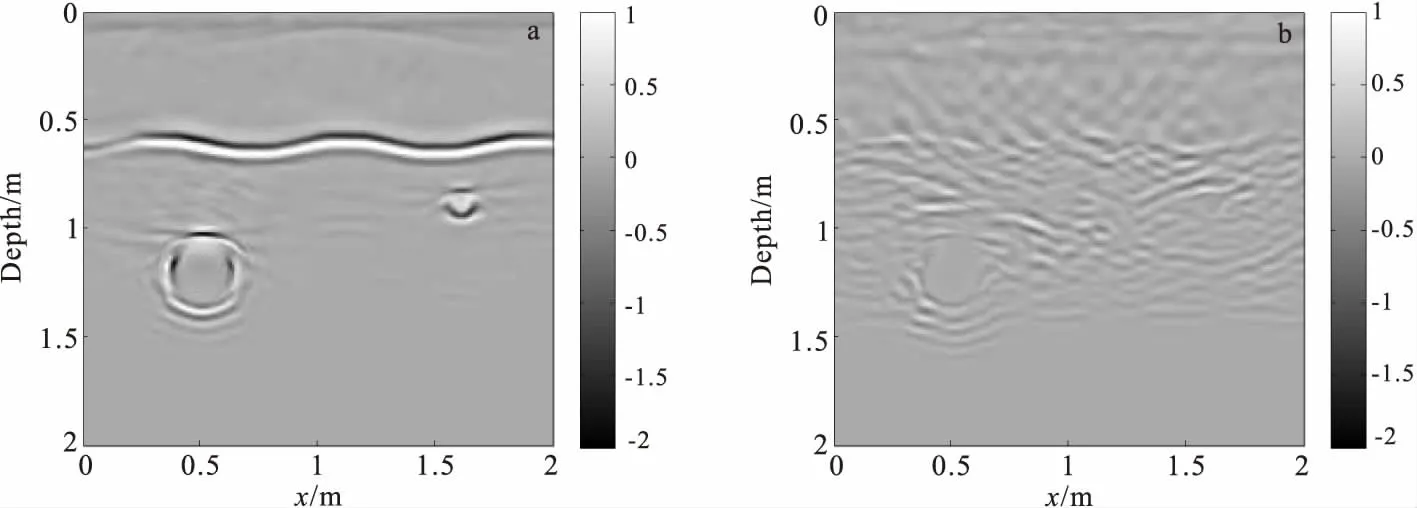
图10 利用图9中的多偏移距正演数据进行逆时偏移获得的成像剖面Fig.10 Imaging results of simulated multi-offset GPR dataset by using the GPR reverse time migration of random media(a)背景介质为均匀介质;(b)背景介质为随机介质
图7(a)为从图6地表中心0.9 m处提取的归一化单道波形能量对比图,对比图3(d)和图7(a)可知,随机介质中的归一化波形能量连续出现多个波峰与波谷,散射波能量收敛差,异常体的空间分布位置难以被识别。而图3(d)中的散射波能量几乎都得到收敛。为了更好地对比空洞位置附近的波形能量收敛性,截取了0.6 m~1.2 m范围内的波形对比如图7(b)所示。由图7可知:自相关长度越小,波形能量越强,且绕射波能量越收敛于空洞的真实位置(如红色虚线表示)处。
3.2 模型二
模型二是大小为2.0 m×2.0 m的复杂GPR模型示意图,如图8(a)所示。模型被一条起伏界面分成上、下两层,起伏界面的埋深约0.6 m;上层介质的相对介电常数为5,电导率为0.02 S/m;下层介质的相对介电常数为10,电导率为0.001 S/m。下层介质的左右两边分别埋有一个圆形空洞异常体,其半径分别为0.15 m和0.05m,圆心位置分别为(0.50 m, 1.2 m)和 (1.60 m, 0.9 m)。图8(b)为图8(a)相应的随机介质模型示意图,其上层介质自相关长度a=1,b=10,方差为0.1,其下层介质自相关长度a=1,b=1,方差为0.1。利用FDTD和逆时偏移成像算法对模型二进行计算时的参数与计算模型一时相同。
图9为利用FDTD法对模型二进行多偏移距正演计算获得的GPR正演剖面。由图9(a)可知,当背景为均匀介质时,电磁波未发生散射,反射波形规则、有序,起伏界面清晰可见;当背景介质为随机介质时,电磁波散射强烈、随机无序传播,散射波相互叠加,如图9(b)所示。由于上层随机介质的自相关长度大,电磁波散射强烈,使得起伏界面的反射波能量异常微弱,无法被识别;而下层随机介质的自相关长度小,电磁波散射较弱,两个圆形空洞的反射波能量较强,能被识别。
利用随机介质GPR叠前逆时偏移算法对图9中的多偏移距正演数据进行逆时偏移,获得的剖面如图10所示。由图10可见,当背景介质为均匀介质时,起伏界面、圆形空洞的成像清晰,反射波和绕射波得到收敛,且归位到其真实空间位置,如图10(a)所示;当背景介质为随机介质时,由于电磁波在其中传播时发生散射,起伏界面的反射波和圆形空洞的双曲线反射波形态失真、扭曲,起伏界面和圆形空洞的反射波能量几乎不能收敛,难以精确定位其空间位置。
通过图10可知:由于介质分布的随机性,电磁波在其中传播时散射强烈,波形发生扭曲,并产生随机扰动使得电磁波在反传过程中不能精确到达真实空间位置,从而造成异常体的逆时偏移成像结果比背景介质为均匀介质的逆时偏移结果差;自相关长度是影响随机介质中异常体成像效果的主要因素,自相关长度越小,异常体的成像越清晰、准确;自相关长度越大,异常体的成像效果越差,且不易被识别。
4 结论
1) 阐述了随机过程的谱分解和混合型自相关函数理论构建GPR随机介质模型方法及其具体步骤;利用FDTD法和归一化互相关成像条件构建了GPR随机介质叠前逆时偏移成像算法。
2) 不同自相关长度的GPR随机介质模型的逆时偏移剖面对比表明:自相关长度是影响异常体成像效果的主要因素;与背景介质为均匀介质的GPR模型的逆时偏移结果相比,随机介质的逆时偏移成像结果的空间分辨率更低,低频噪声更强。

