湍流渠道中几何减阻技术及其机理研究

许桂阳，王春光，龚建良，张晓军，邓 哲

（西安近代化学研究所，西安，710065）

0 引 言

20世纪70年代NASA兰利研究中心发现，顺流向的微小沟槽（肋条）表面能有效降低壁面摩阻，且具有一定尺度的三角形（V型）沟槽为最佳减阻沟槽几何形状。在流动状态下，减少因流体的黏性而产生的黏性阻力具有重要意义[1]。

文献[2]进行了关于层流状态下沟槽渠道阻力系数变化规律的研究。文献[2]主要针对具有任意形状和任意方向的沟槽渠道中参数变化对阻力系数的影响，同时还分析了表面简单褶皱引起减阻的相关机理[3]。褶皱影响黏性阻力是由于它改变了壁面表面的剪应力分布以及湿周的面积[4～6]。然而以上研究主要集中在层流几何减阻方面，而现在更为关注沿着沟槽方向的流动减阻，特别是表面肋条减阻技术[7～9]，这种技术主要是控制边界层内的湍流结构，特别是拟序结构，从而达到控制湍流动能损耗，实现减阻目的[10～18]。

本文主要研究了具有湍流流动的渠道中，用一阶傅里叶模式表示任意壁面形状时，通过改变壁面的几何形状，实现渠道的减阻系数的变化。为了方便计算简化模型，建立单位计算模型。通过通用流场分析软件Fluent对流动过程进行计算，选取kω− SST模型对湍流模型进行模拟，并计算压降损失。对减阻系数变化规律以及其内在机理进行详细的分析。

1 计算模型和方法

假设存在一个流动充分的渠道，流体的流动状态为湍流状态，由压降驱动其沿一个方向延伸至±∞，流体被波浪壁上、下表面约束，见图1。上表面和下表面的几何形状分别由傅里叶函数表达形式U()Y x和L()Yx进行近似。上、下表面的平均位置分别在Y H=± 处，如式（1）所示。

图1 任意壁面渠道模型示意Fig.1 Channel Bounded by Volatility Upper and Lower WallsH—半渠道的高度

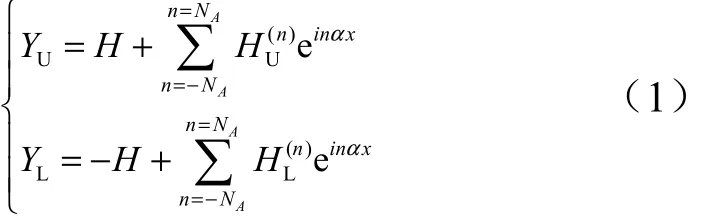
为简化模型，仅选取下壁面具有波浪壁的情况进行研究，上壁面假设为直壁面。选取一阶傅里叶模式对任意波浪壁形状进行近似，同时选取H作为特征长度，对模型进行单位化，设 /yYH= ，则单位化后的上、下表面函数表达式为

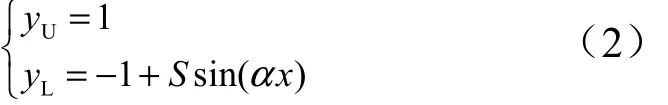
式中Uy，Ly分别为渠道上、下表面的几何形状；S为波浪壁的幅值；α为波数，且建立计算模型，只选取一个周期的波数进行研究，模型的前后、左右设定为周期边界条件，流动方向选取单位长度“1”。单位化后的模型如图2所示。

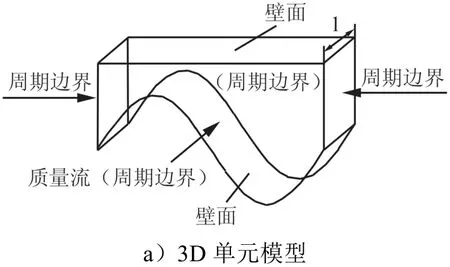
图2 单位化模型Fig.2 Unit Model

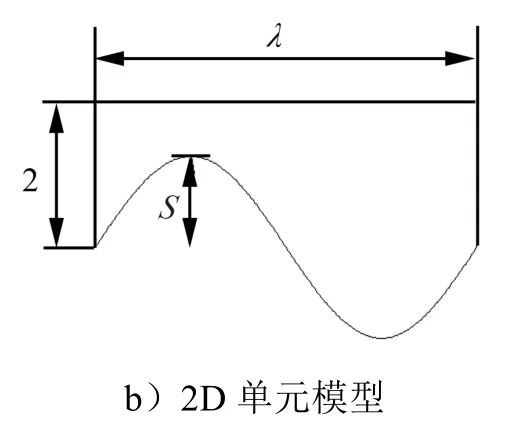
续图2

Fluent中的计算模型如图3所示。网格由ANSYS ICEM CFD 14.5生成，利用块技术生成高质量的结构化网格，且沿着壁面方向进行加密，以保证近壁面位置的计算精度，网格总数为40 000。

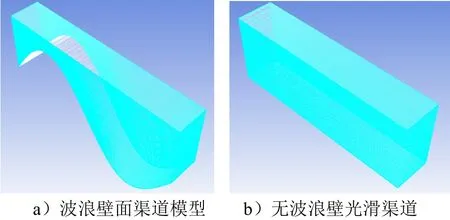
图3 Fluent计算网格Fig.3 Fluent Calculation Grids

对网格的有效性进行校验，输出上、下壁面y+均小于 1，说明 Fluent的自带函数可以较精确地计算近壁面的黏性底层内的问题。结果的收敛残差设置为小于本地残差 10-7，并且选取二阶迎风格式来计算所有的平衡方程。

计算方法及有效性验证已在文献[19]中作详细阐述，此处不再赘述。

2 振幅和波数对减阻效果的影响

波浪壁的幅值S、波数α以及流动状态的变化都会影响压强的损失，下面分别针对不同的幅值、波数进行计算，研究减阻系数随其变化规律。

将Re固定在2648，幅值S从0.25变化到1.5，波数由0.1变化到1.2，计算不同状态下的减阻系数 'f，结算结果如图4所示。从图4中可以看出，减阻系数随着波数的增加单调变化。当波数α较小时，可以获得较大的减阻效果，最大可以达到 25%。然而，当波数α较大时，减阻系数 'f将大于 0，即此时的几何结构已经没有减阻功能，相比于无波浪壁的渠道，反而是增加了阻力。当研究幅值S对减阻系数的影响规律时，应该将波长λ分为2种情况，即长波长（α≤0.7）和短波长（α≥0.8）两种情况。由于只关注减阻，因此只关注长波长状态下幅值S对减阻系数的影响，即图4中减阻系数小于0的结果。

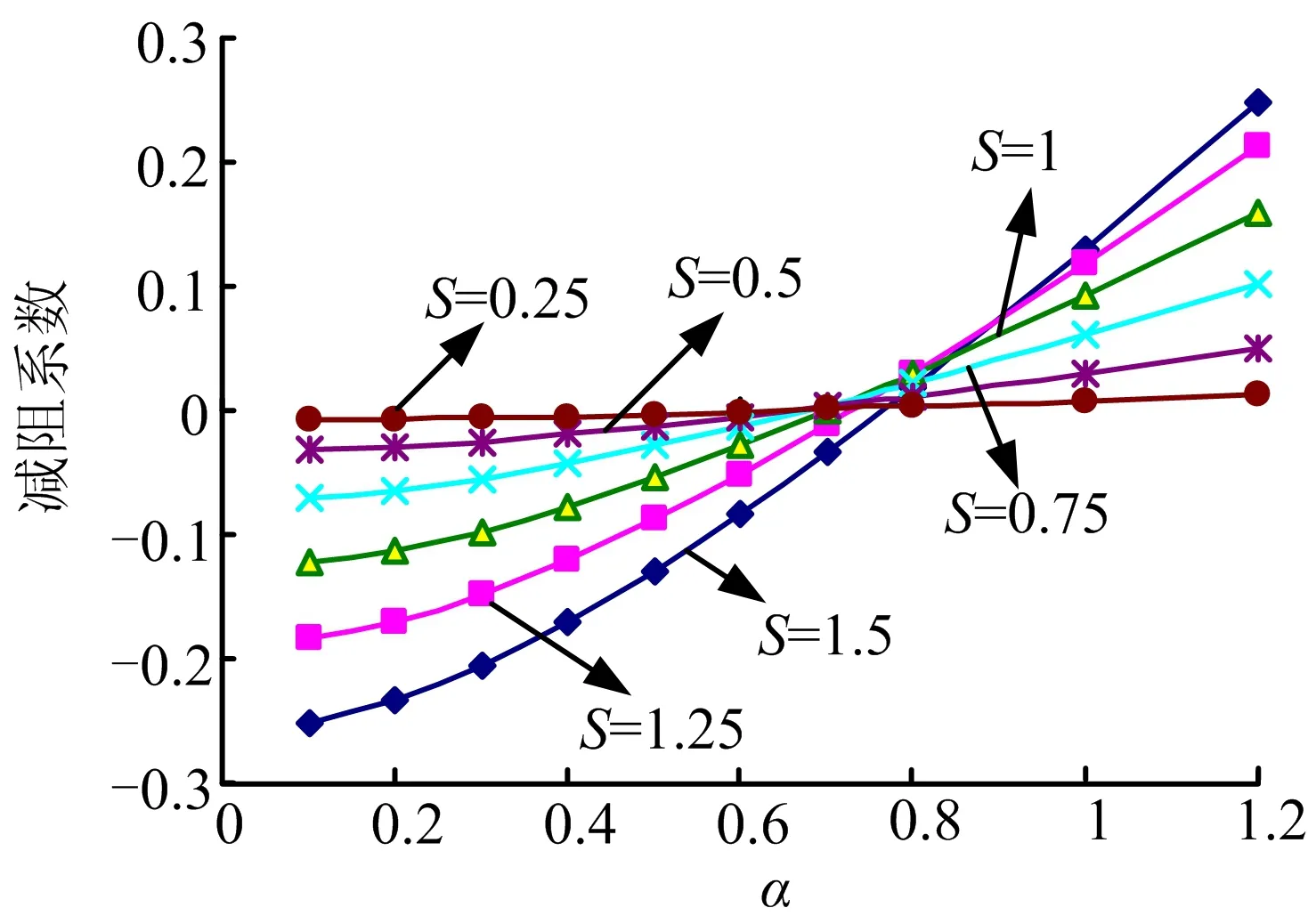
图4 减阻系数随几何形状的变化规律（Re=2648）Fig.4 Drag Reduction Factor Changing with the Geometry

2.1 波数对减阻系数的影响

为了研究波数α对减阻系数影响的内在原因，将幅值S固定在0.75，渠道截面z方向的速度分布随α的变化规律如图5所示，图5中的速度场是以无波浪壁渠道的中心速度为基础进行单位化处理后的结果。

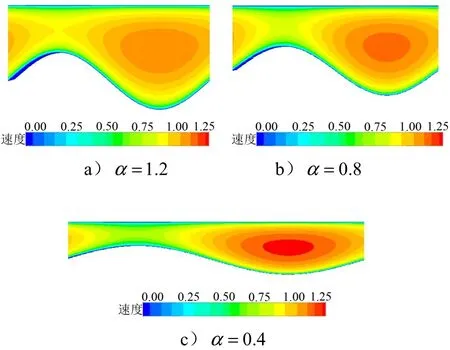
图5 速度分布随波数变化（ 0.75S= ）Fig.5 Velocity Distribution of the Grooved Channel（ 0.75S= ）

随着波数的变化，速度的分布也在变化。当波数降低时，流体在渠道中心的速度增加，壁面附近的流速降低，相当于大部分质量都从中心通过。对于湍流流动，近壁面位置都有一层黏性底层，剪切应力与速度密切相关，可通过式（3）求出：

因此，波数的变化将导致d/du y变化，从而导致壁面剪切应力的变化。将不同波数α条件下剪应力沿壁面变化曲线输出，以无波浪壁渠道的剪应力为基础进行单位化处理，如图6所示。由图6a可以看出，在无波浪壁的渠道中，上下壁面的剪切应力比都保持在1；如图 6b所示（图中数值表示波数α），当α较小时，上、下壁面的剪应力分布非常接近。随α增大，下壁面的剪切应力分布一直保持正弦曲线的变化趋势，而上壁面的剪切应力随波数变化较为“剧烈”。

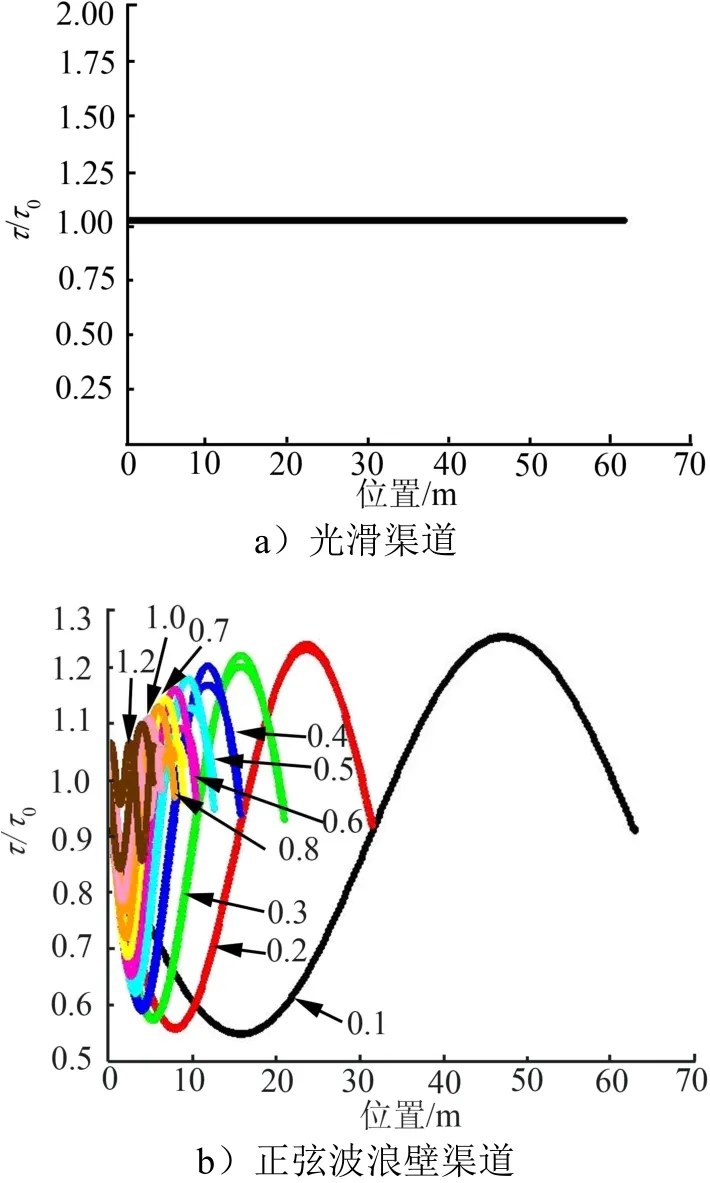
图6 剪应力分随波数变化规律（ 0.75S= ）Fig.6 The Shear Stress Distribution of Walls of the Grooves Sections（ 0.75S= ）

α较小时，剪应力比“振动”幅度较大，但是均值接近1。α较大时，剪应力比“振动”剧烈，剪应力比均值明显大于1。

输出上、下壁面的剪切应力，并根据平衡原理，相应的压降为

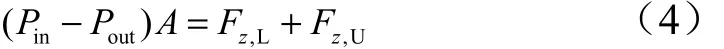
式中,LzF 为下壁面的剪应力沿z方向合力，。,UzF 为上壁面的剪应力z方向合力，的剪应力，可通过Fluent计算结果直接输出。

式（4）计算所得的压降与Fluent直接输出的压降对比结果如图7所示。从图7中可以看出，随波数α增加，压降单调增加，因此必然导致阻力增加，相应波浪壁几何结构的减阻能力逐渐降低。

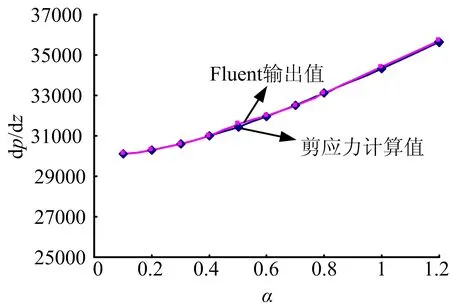
图7 由剪应力计算所得的压降与Fluent直接输出值对比（ 0.75S= ）Fig.7 Comparison of dp/dz Calculated by Shear Stress and Fluent（ 0.75S= ）

2.2 幅值对减阻系数的影响

为了研究波浪壁幅值S对减阻系数的影响，将波数α固定在0.7，分别计算当幅值S=0.25～1.5情况下的压降及减阻系数，输出相应z方向的速度随幅值变化情况，如图8所示。图8中的速度场是以无波浪壁渠道的中心速度为基础进行单位化处理后的结果。

图8 速度分布随幅值变化（0.7α=）Fig.8 Velocity Distribution of the Grooved Channel（0.7α=）

从图8可以看出，与波数变化类似，幅值变化时，会导致流体的速度分布变化，从而影响近壁面的剪应力分布变化，从而影响压降。

为了研究其剪应力随幅值的变化规律，将不同幅值情况下的剪应力输出，如图9所示。从图9中可以看出，下壁面的剪应力分布一直保持余弦形式。随幅值增加，上壁面的剪应力变化幅度逐渐增大。当S=0.25时，上下壁面剪应力比几乎相同，较接近无波浪壁渠道壁面的值1。当S=1.5时，上下壁面的剪应力变化趋势明显不同。从图9中可以看出，幅值的减小相当于将整个剪应力的分布“压”的更加扁平，而均值也在增加。

图9 剪应力分布随幅值变化（0.7α=）Fig.9 The Shear Stress Distribution of Walls（0.7α=）

同样输出不同情况下的剪应力，并根据平衡原理计算相应的压降，与Fluent直接计算值对比，如图10所示。

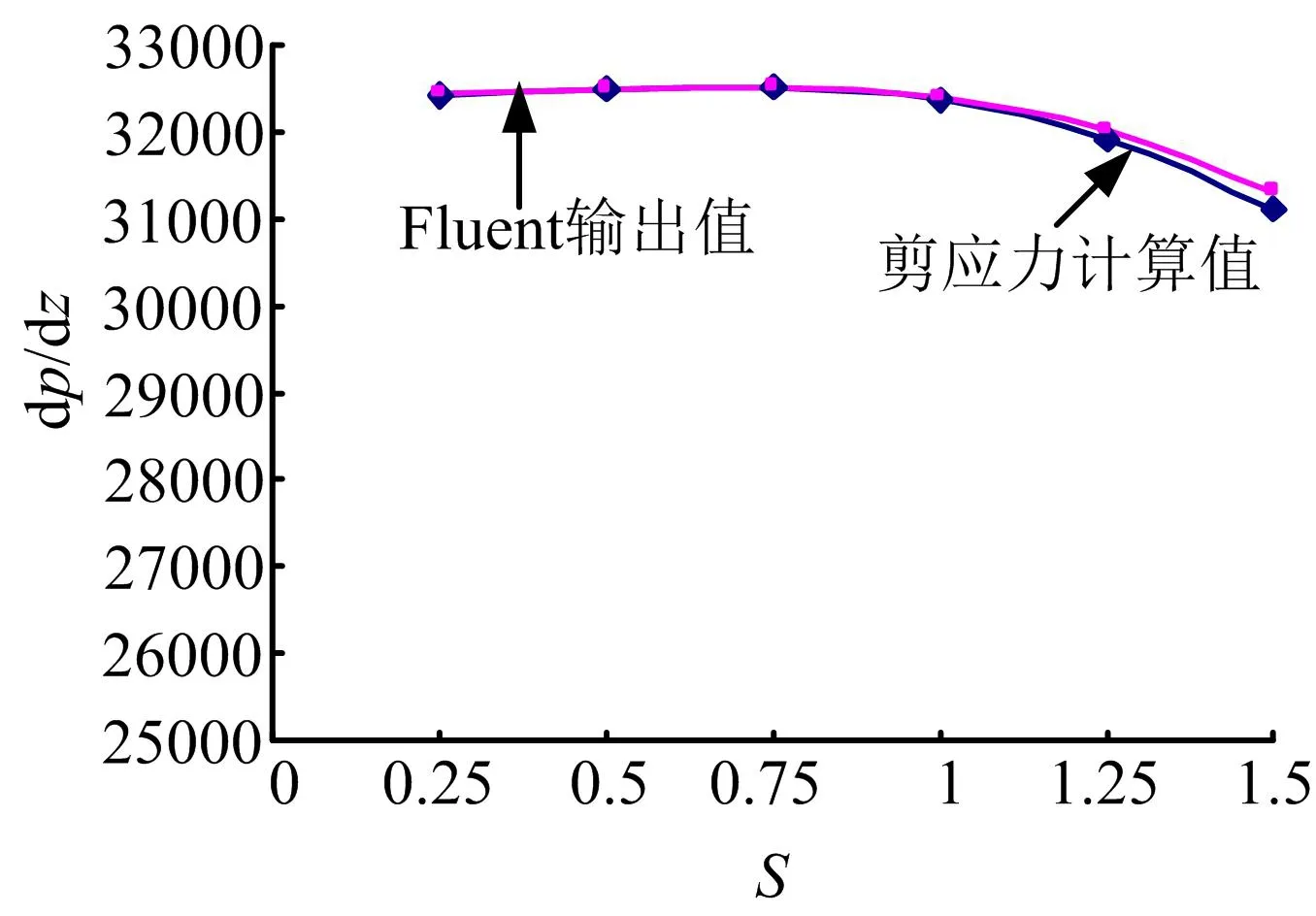
图10 由剪应力计算所得的压降与Fluent直接输出值对比（0.7α=）Fig.10 Comparison of dp/dz Calculated by Shear Stress and Fluent（0.7α=）

由图10可以看出，随幅值增加，阻力损失降低，减阻效果增加，波浪壁的减阻能力增加。

2.3 短波情况下减阻系数的分析

从图10可以看出，在短波长波浪壁的情况下，当波数进一步增加时，阻力将会进一步增加。分析这种现象的原因为：当波数增加时，将导致两边的壁面向中间聚拢，会增加渠道内的黏性摩擦，阻碍流体的流动，如文献[6]所述，有效通道面积将会降低，特别是在较大幅值情况下，更为明显。当α→∞时，有效通道面积将会减小到（2-S）·λ，导致壁面加厚，通道面积减小，阻力增加。

所以，在短波长情况下，即波数α较大时，渠道的阻力将会增加，特别是在较大的幅值S情况下，更为明显。

3 任意几何形状波浪壁对压降的影响

为了不失一般性，建立几种不同形状的波浪壁，保证通道面积相同，同时具有相同的幅值S和波数α，具体如图11所示。对于任意几何形状，主要分为2种类型：a）等深度几何形状，即波浪壁的深度和高度相同，波浪壁分布在底边平均位置y=-1两侧；b）非等深度几何模型，即为单侧波浪壁，波浪壁的深度和高度并不相同。

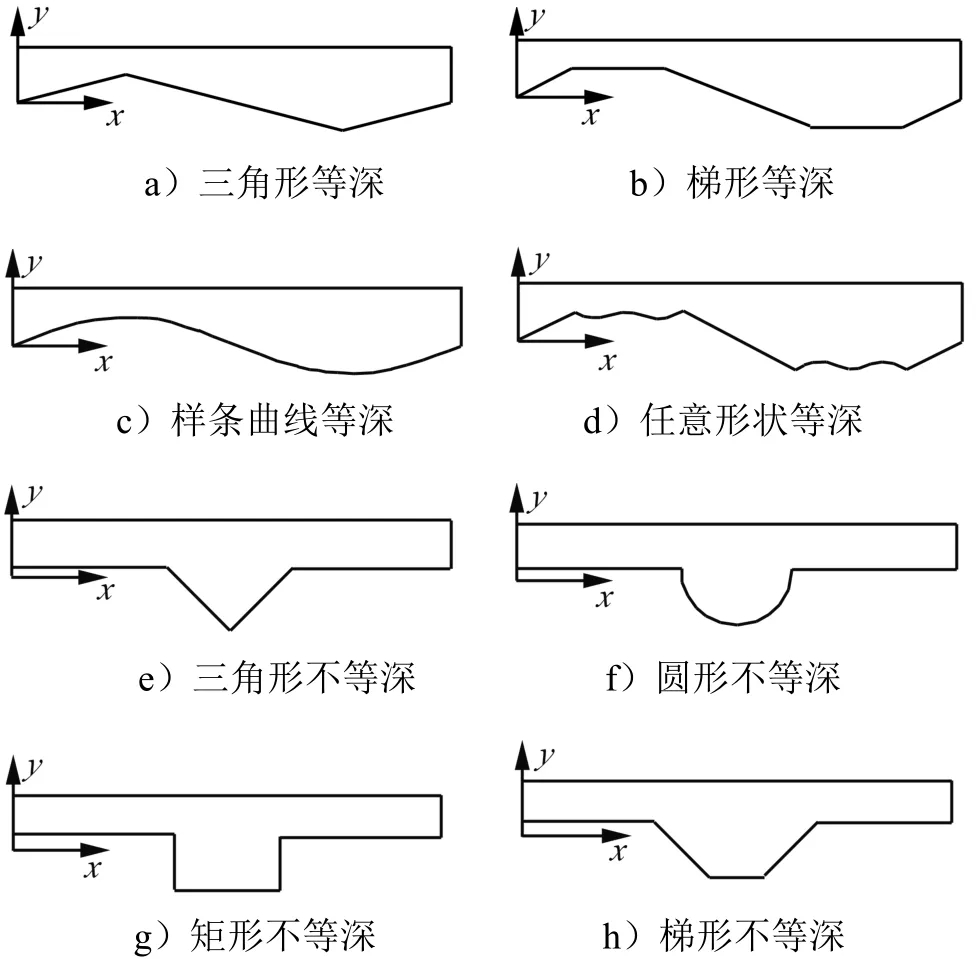
图11 不同的波浪壁形状Fig.11 Different Geometries of Volatility

建立不同几何形状渠道的流场计算模型，在相同的输入条件下进行计算，得到不同形状下的压降与无波浪壁压降之比，如表1所示。

表1 不同形状波浪壁的压降及与正弦波浪壁的差别Tab.1 Pressure Drop and Difference Between SinusoidalGeometry

从表1中可以看出，除几何形状f和g外，正弦几何形状的压降都与任意形状波浪壁很接近，差异在10%以内。

相比于e和h，f和g的几何形状有明显的向内尖角（角度小于等于90°），该尖角位置的黏性底层厚度急剧减薄，速度变化率d/du y增加。输出f和g的剪应力分布，如图12所示。从图12可以看出，在向内尖角位置剪应力数值很大，远远大于平均值，分析认为正是因为该尖角处的剪应力集中，导致渠道的压降更大，阻力损失更大，不利于减阻效果的提高。因此，在减阻设计时应该尽量避免向内尖角（角度小于等于90°）的几何形状出现。

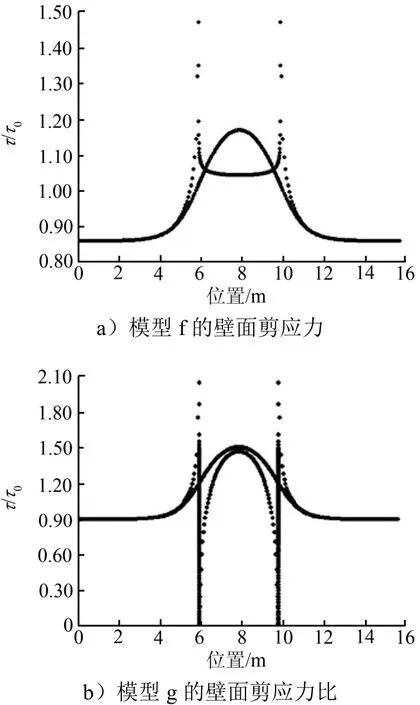
图12 壁面剪应力分布Fig.12 Shear Stress Distribution of Walls

4 不同来流条件计算结果

选取Re=10 000情况进行相同模型尺度的计算，只计算长波长情况下不同几何模型减阻系数变化规律，如图13所示。

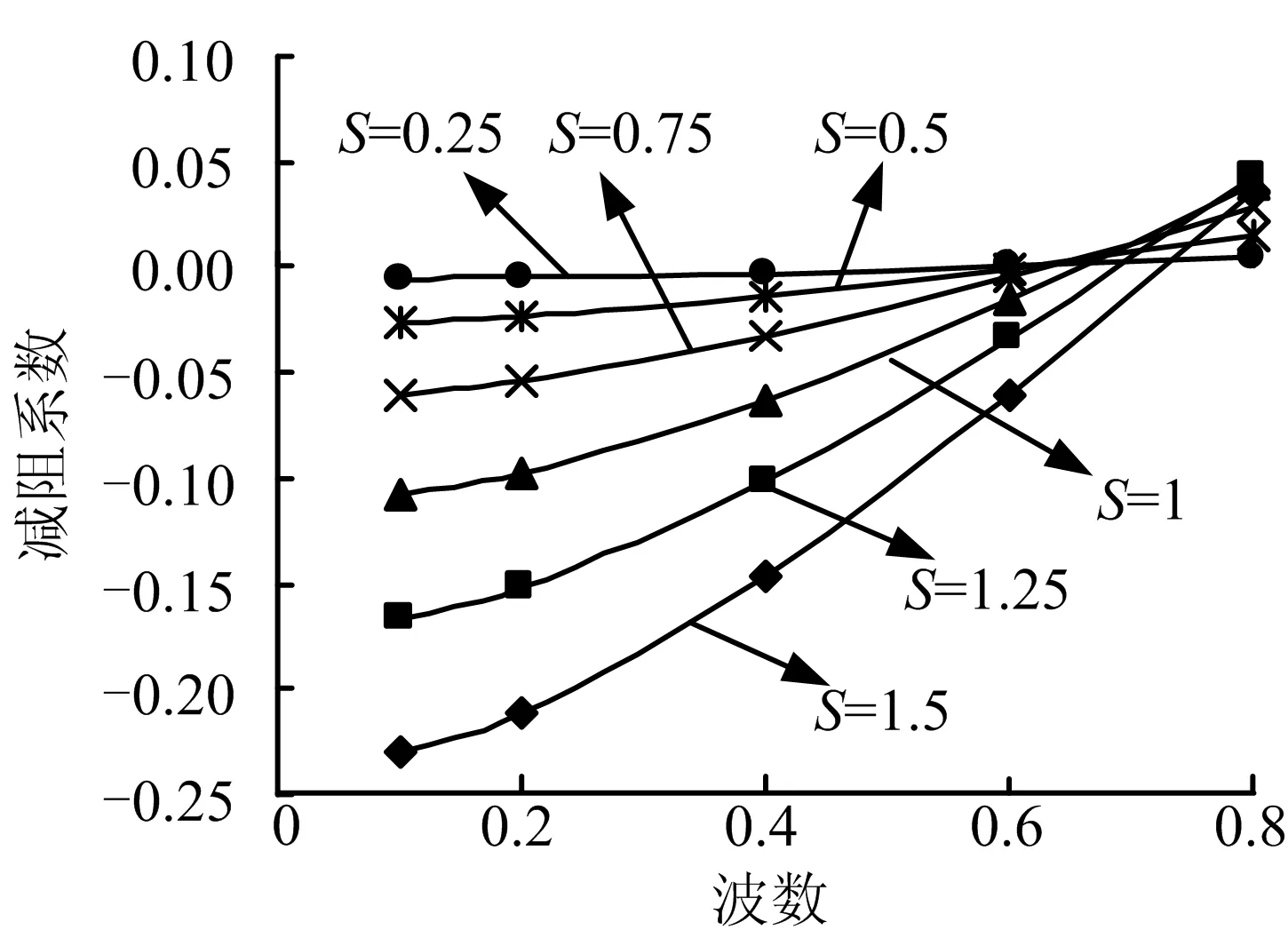
图13 减阻系数随几何形状的变化规律（Re=10 000）Fig.13 Drag Reduction Factor Changing with the Geometry

从图13中可以看出，该条件下的减阻系数变化规律与Re=2648情况下相同，波数α越小、幅值S越大，减阻效果越好。

5 结 论

a）壁面几何形状用一阶傅里叶级数近似时，当波浪壁的波数α减小时，减阻效果会单调增加。当考虑波浪壁槽幅值的影响时，需要分2种情况进行考虑，即长波长情况和短波长情况。当波数α小于0.7时，增加幅值有利于增加减阻效果；当波数α大于0.8时，增加幅值减阻效果将会降低，甚至出现增加阻力现象。

b）随着波数α变化，渠道截面的速度分布变化，壁面附近的黏性底层内的速度同样会变化剧烈。所以α的变化将导致壁面上剪切应力分布变化。α减小时，上、下壁面的剪切应力更加接近，整体变化范围较大，而平均值是在逐渐降低，减阻效果增加。α增大时，剪切应力的“振动频率”会更加剧烈，均值增加，从而减阻效果减弱。

c）在长波长的情况下，当α保持不变时，剪应力变化幅度将会随波浪壁幅值S的减小而降低，从而更加接近直渠道值，减阻效果降低；在短波长情况下，波数α的增加相当于使壁面聚拢，将会增加黏性阻力，阻碍内部流体的流动，使有效渠道面积降低，特别是在幅值较大的时候更加明显。因此，想要获得更大的减阻效果，应该尽量选取较小的波数α，同时尽量增加波浪壁幅值的大小。

d）对于任意的几何形状的波浪壁，大部分情况下，一阶傅里叶模式都有很好地近似，可以使压降的差异控制在10%以内。但是当几何形状出现向内尖角时（角度小于等于90°），将会使壁面附近的黏性底层厚度急剧减薄，从而使尖角处的剪切应力急剧增大，使整体压降增大，不利于增加减阻效果。