一种基于因子图的异步信息融合定位算法
张 靖,王向东,邓志宝,张凌东,刘宇航
(1. 北京航天发射技术研究所,北京,100076;2. 火箭军驻211厂军事代表室,北京,100076)
0 引 言
单一惯性定位方法已无法满足陆基武器发射系统在复杂工况中大范围机动、随机发射的定位需求,不具备良好的鲁棒性与可靠性[1],难以持续提供高精度的定位信息。基于多信息源融合的组合定位算法实现了多种定位传感器的优势互补,可在复杂工况中提供高精度的定位信息,提升导弹武器系统的生存能力。
按信号的输出频率特性划分,目前定位信息源主要分为3类:a)信号以固定频率发送的信息源,如惯导(Inertial Navigation System,INS)、里程计(Odometer,OD)、全球卫星导航系统(Global Navigation Satellite System,GNSS)等;b)信号异步非等时间间隔输出的信息源,如地磁匹配(Geomagnetic Matching Navigation System,GMNS)、地图匹配(Map Matching Navigation System,MMNS)、景象匹配(Scene Matching Navigation System,SMNS)等;c)距离间隔较长、不等时间间隔信号输出的信息源,如地标。组合定位算法在融合不同频率特性的信息源时存在异步时间配准误差,降低定位精度。
解决多信息源异步融合问题,主要有3种思路:a)采用GMNS、MMNS等信息源输出的异步非等间隔定位信息直接校正INS的位置,该方式对匹配定位信息利用不充分。b)在数据融合前消除时间不同步问题。文献[2]采用最小二乘法将高频量测值融合到低频量测时刻进行同步,文献[3]、文献[4]采用内插外推将高精度量测数据推算到低精度量测信息的时间点上;c)针对异步量测信息采用异步融合方法,可避免以上两种方法均存在数据拟合误差。文献[5]采取各个子滤波器滤波周期的最大公约数和最小公倍数作为融合周期,但不适用于信号无固定频率非等间隔输出的信息源。
本文提出了一种基于因子图的异步多源组合定位算法,以异步量测信息异步融合的思想,采取量测信息“即来即更新”的状态估计方式,充分利用了信息源的量测信息,避免了外推法的拟合误差,适用于多频率特性传感器的数据融合,可实现定位信息源的即插即用。
1 系统误差模型
组合导航系统的离散化误差模型为

式中 xk为系统的状态变量; zk为系统的观测变量;为转移矩阵和观测矩阵; wk, vk为噪声项,设 Qk, Rk为噪声项 wk,vk的协方差矩阵;i表示有i个观测方程。采用表示INS/OD组合的观测方程。表示 INS/GMNS组合的观测方程。
2 因子图与和积算法
2.1 因子图
因子图是一种概率图模型,用来表示全局函数与局部函数的关系,可以将多变量全局函数因式分解后的多个局部函数进行图形化表示。因子图模型G=(F , X,ε)包含因子节点:fi∈F、变量节点:xj∈X和边:eij∈ε3个元素[6]。因子图可将待求解的问题转化为边界问题,在很多领域如编译码、信号处理、人工智能、神经网络中的边界问题都可用因子图算法表示并求解,因此,因子图作为一种分析问题的图形工具已经得到了广泛的应用[7]。
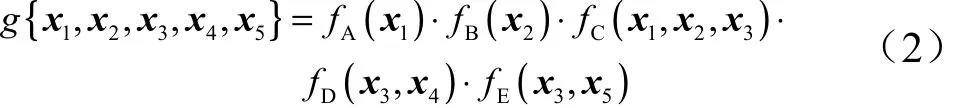
变量 xi以变量节点形式来呈现,局部函数 fj( Xj)以函数节点的形式来呈现。当变量 xi与某个局部函数fj( Xj)相关时,则在因子图中用双向边将两者对应的节点相连接。
基于上述分析,式(2)对应的因子图模型见图1。
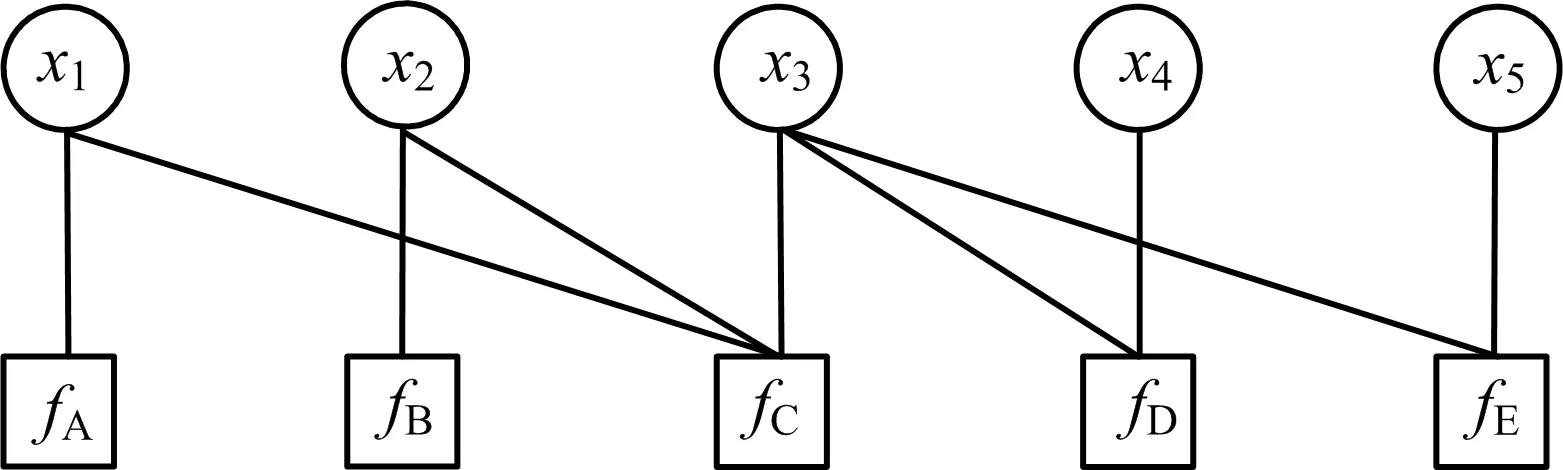
图1 对应因子图模型Fig.1 Corresponding Factor Graph Model
2.2 和积算法
因子图可以清晰直观地表现函数与随机变量间的关系,而对应函数节点与变量节点间的消息传递则需要和积算法来实现。和积算法作为一种消息传递算法,又称置信传播算法,用来计算因子图中各节点沿着不同边传递的信息,规则如下:
在因子图中,某个节点x传递到另一个节点f的信息可以从其他所有与节点x相关联的节点传递到x节点的消息乘积而得。
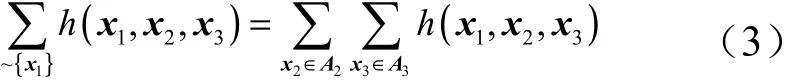
变量节点x传递到函数节点f的消息:
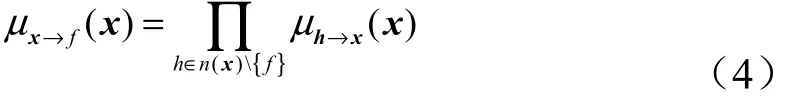
变量节点f传递到函数节点x的消息:
式中 X=n(f)表示节点f的所有相邻节点即函数f包含的所有变量组成的集合;~x表示除去节点x的所有变量集。
3 异步非等间隔数据融合算法
在线性高斯系统(Linear Gaussian,LG)中,运动方程、观测方程是线性的,且两个噪声项服从零均值的高斯分布,记高斯分布的概率密度函数为
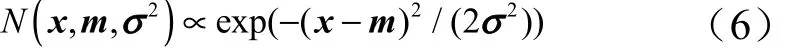
式中 m和2σ为均值和方差,且服从以下计算:
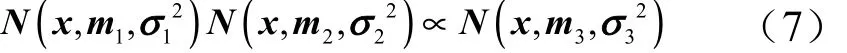
其中,

同样地,可以得到:
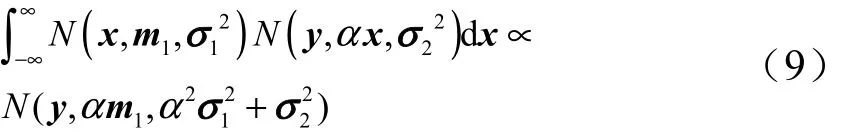
组合导航是由观测量估计状态量的过程,系统的状态变量为:x1, x2,…xk,系统的观测量为,状态变量估计的条件概率密度可写为,假设模型的一阶马尔可夫性,根据贝叶斯法则得到:


图2 惯导/里程计/地磁匹配组合定位状态估计因子图示意Fig.2 State Estimation Factor Graph Representation for Inertial Navigation/Odometer/Geomagnetic Matching Integrated Navigation
最小方差估计等于量测为某具体实现条件下的条件均值[9]:
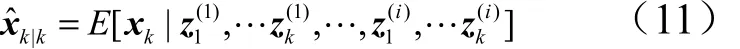
式中kx的条件概率密度函数为时刻k的边缘函数:
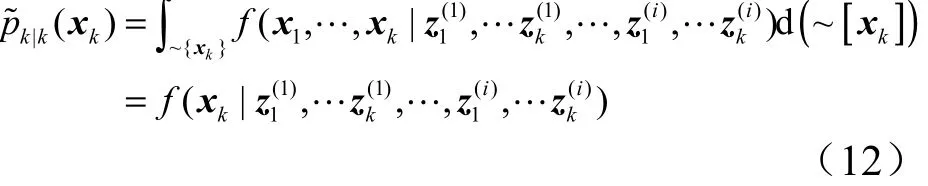
式(12)的计算需用到和积算法,并用积分作为求和操作,见式(4)、式(5)。再将式(10)代入式(12),得到:
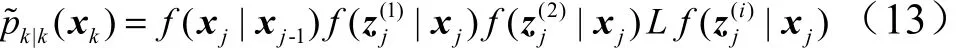
采用式(9)的计算方法整理得到,为推导过程简洁、直观,以下采用向量、矩阵采用一维状态形式进行推导:
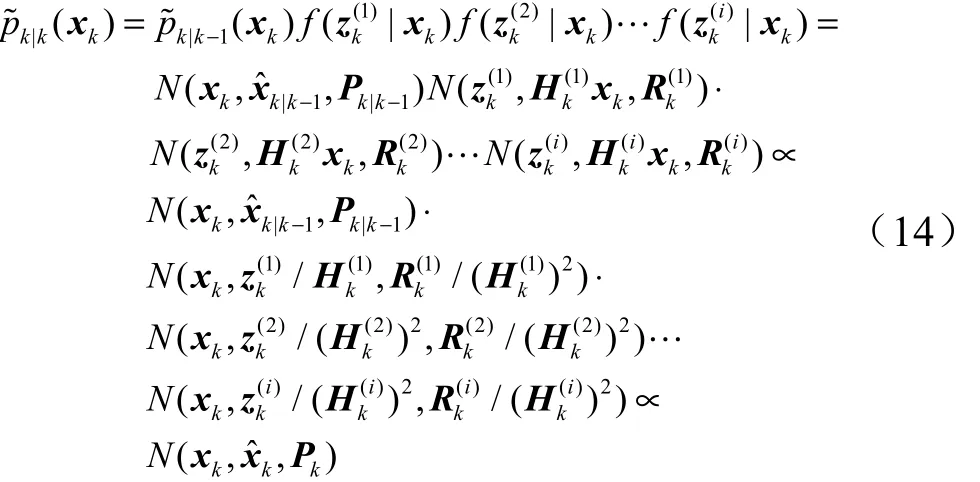
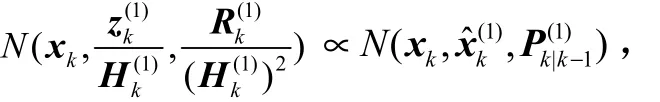
其中,

再令:

其中,
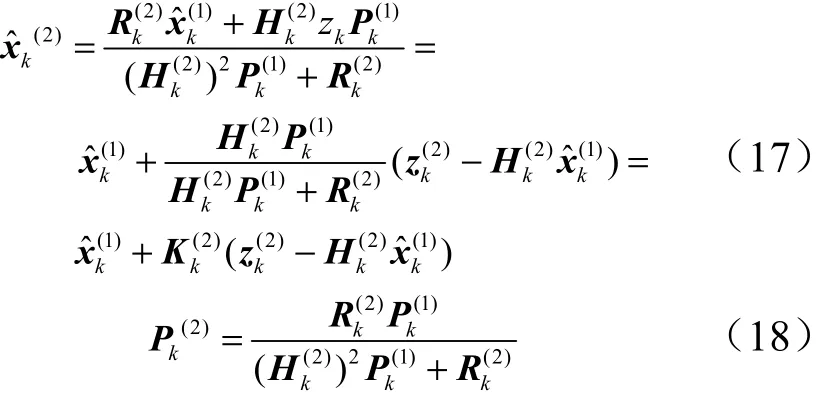
迭代进行计算,得到:

令:

同样地,通过式(12)可以得到:
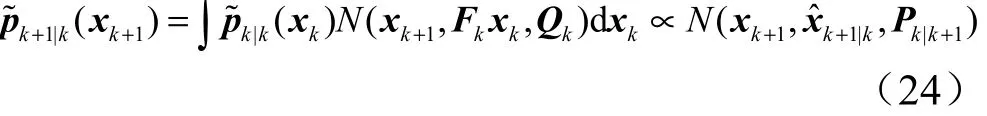
其中,
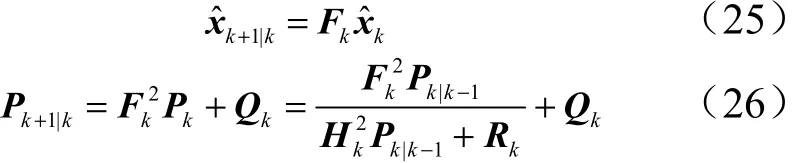
异步多源组合定位算法流程如图3所示,INS/OD的信号同频且高频输出,GMNS的信号非等间隔输出。若无 GMNS信号更新,进行一次时间更新,一次INS/OD组合的量测更新,若有GMNS信号更新,进行一次时间更新,进行两次量测迭代更新,见式(19)、式(20)。

图3 异步多源组合定位算法流程Fig.3 Asynchronous Multi-source Integrated Navigation Algorithm Flow Diagram
4 仿真分析
选取INS、OD和GMNS 3种定位传感器进行仿真分析,INS、OD的信号以100 Hz的频率输出,GMNS的信号在1~10 s之间非等间隔输出。采用异步多源组合定位算法、GMNS定位结果直接校正惯导位置这两种组合定位方法进行仿真,对结果进行比较分析。
4.1 行车路径与状态
以 WGS84坐标系统设置起始点为:经度116.40675°E,纬度39.80047°N,高度H为70 m。
行车状态如表1所示,全程共计用时4095 s,里程约为80 km。行驶路径和行驶方向如图4所示。
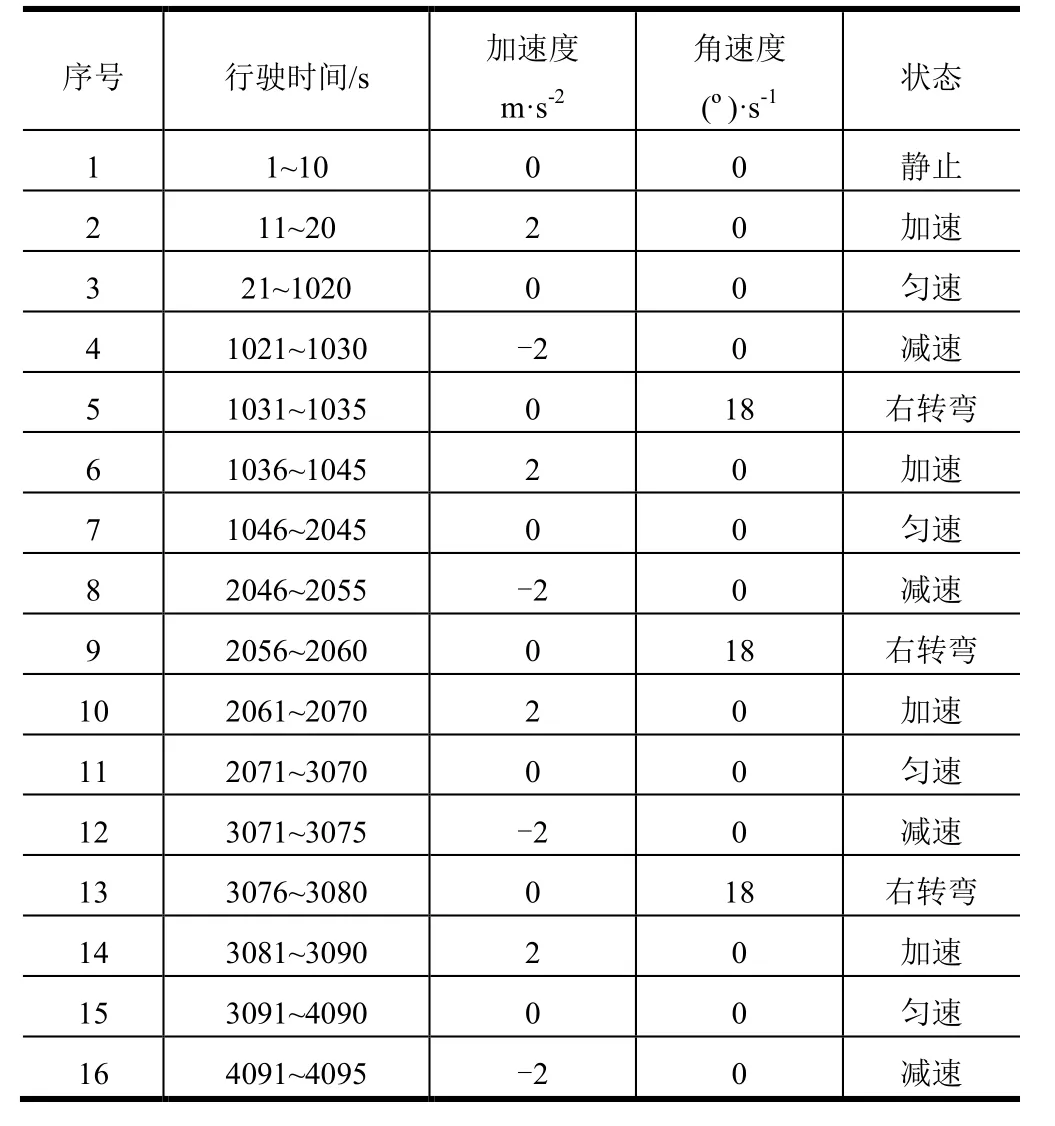
表1 行车状态Tab.1 Driving Status
图4 仿真路径Fig.4 Simulation Path Chart
4.2 误差参数设置
以90TM型二频机抖激光陀螺仪为参考,取陀螺随机常值零偏为 0.003 (°)/h,随机游走系数为0.0005 (°)/h;加速度计零偏为20 µg;地磁匹配水平误差为10 m(1σ),高程误差10 m(1σ);里程计刻度系数误差为 0.01;里程计杆臂误差为[0.0149 m,0.1756 m,-1.0232 m];地磁匹配杆臂误差为[0.0149 m,0.1756 m,1.0232 m]。
4.3 仿真结果
依据第4.1节路径与第4.2节误差参数的设置生成了8组行车数据,分别采用本文提出的异步多源组合定位算法、GMNS结果直接修正惯导位置的组合导航算法进行仿真分析,随机选取一组仿真结果的北向、东向与高程定位误差对比分别如图5~7所示。图5a、图6a、图7a为采用异步融合算法的组合导航定位误差,精度为:北向10.2 m(3σ)、东向10.5 m(3σ)、高程4.9 m(3σ);图5b、图6b、图7b为采用GMNS结果直接校正INS位置的组合导航定位误差,精度为:北向29.9 m(3σ)、东向30.1 m(3σ)、高程15.1 m(3σ)。从仿真结果可以看出,采用异步非等间隔融合算法的水平与高程定位误差分别减少到采用匹配点直接校正惯导位置方法的三分之一。
通过对比两种组合导航算法的定位误差图可以看出,直接运用GMNS结果校正惯导位置时,导航过程中定位误差有突跳的状态,如图 5~7的箭头所示;采用异步融合算法会将定位误差的幅值压缩、平滑,定位精度更高。
行驶过程中北向与东向的陀螺零偏状态估计对比如图8、图9所示。从图8、图9可知,采用异步融合算法进行导航的过程中,2000 s之后东向陀螺零偏估计值稳定在0.003 (°)/h左右,3000 s之后北向陀螺零偏估计值稳定在0.003 (°)/h左右。这是由于GMNS提供了较为准确的位置观测信息,使东向陀螺零偏得到较好的估计。
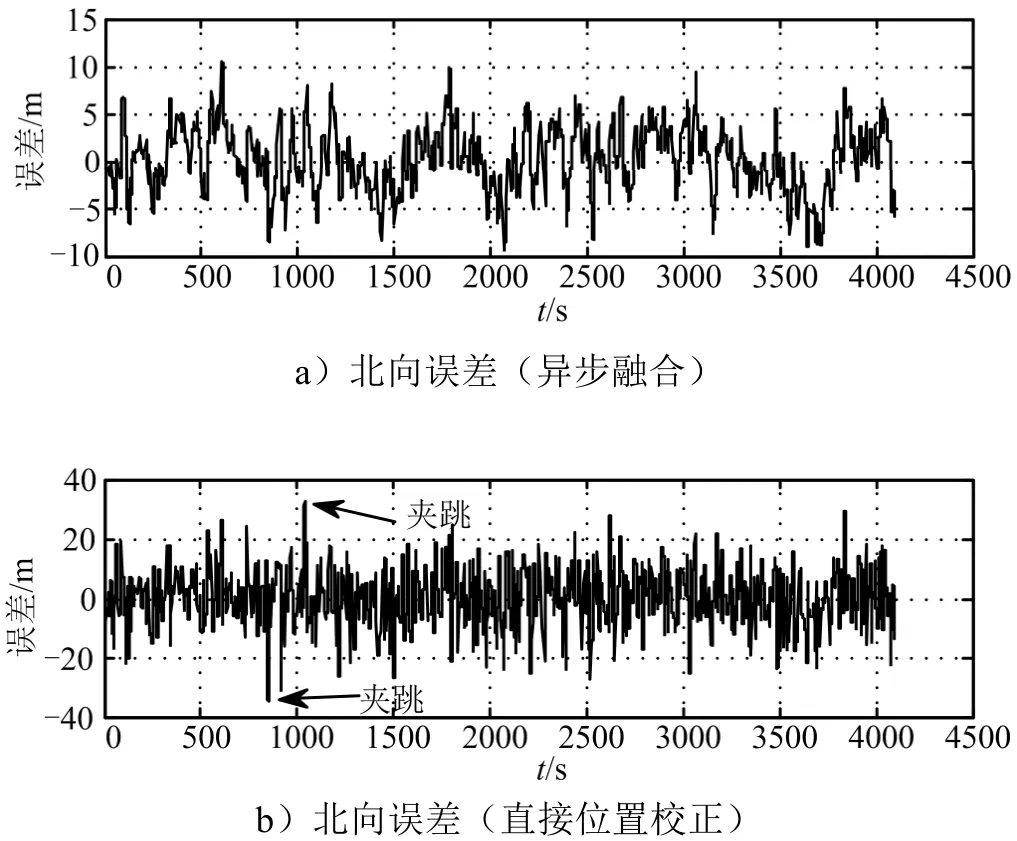
图5 北向误差对比Fig.5 Northbound Error Comparison Chart
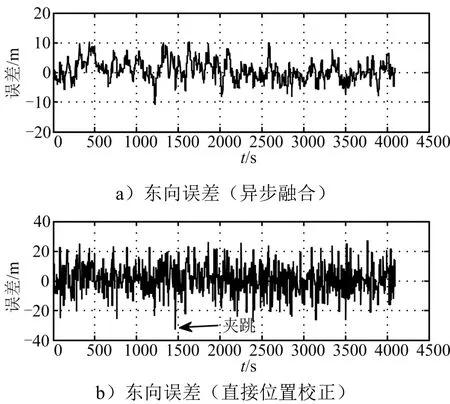
图6 东向误差对比Fig.6 Eastward Error Comparison Chart

图7 高度误差对比Fig.7 Height Error Comparison Chart
采用GMNS结果直接校正惯导位置,导航过程中由于缺少一种较为准确的观测量,东、北向陀螺零偏的收敛在 0.0025 (°)/h左右,较初始设置偏差了0.0005 (°)/h。
水平轴陀螺零偏与位置误差在一定时长内呈大致线性关系[10],式(26)为作用在东向轴线的有效角速率零偏(gEδB)引起的位置误差。
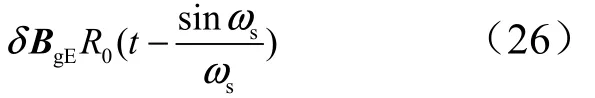
式中0R为地球半径;sω为舒勒振荡频率。采用异步融合算法可对陀螺零偏进行更准确的实时校正,更加有效的抑制了位置误差发散,提高定位精度。

图8 北向陀螺零偏估计对比Fig.8 Northbound Gyro Bias Estimation Comparison Chart
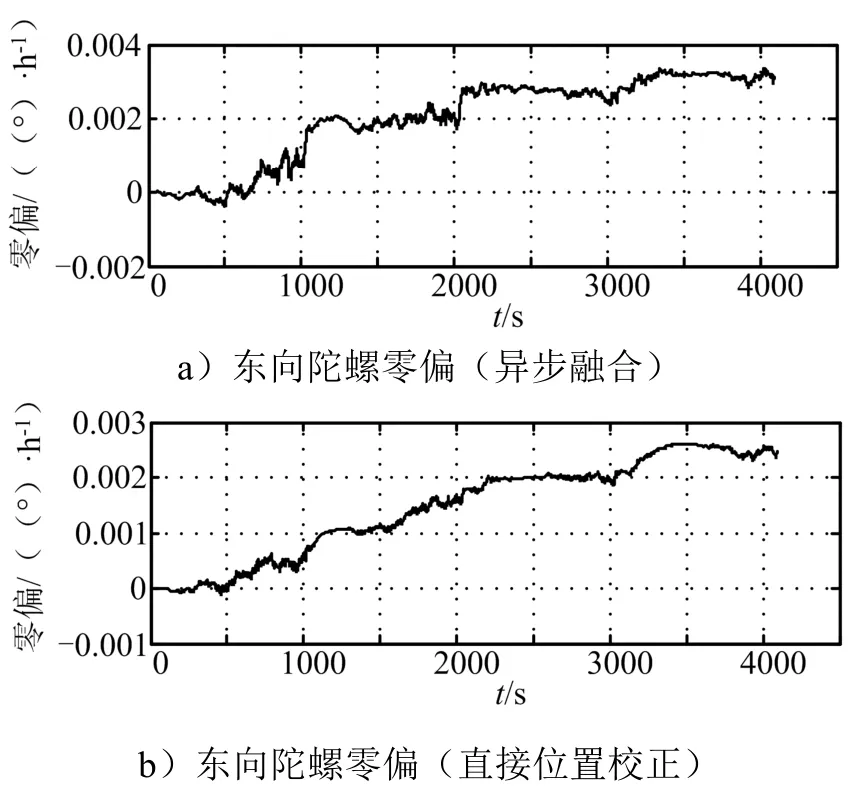
图9 东向陀螺零偏估计对比Fig.9 Eastward Gyro Bias Estimation Comparison Chart
5 实车试验
采用 SINS、GNSS、里程计和高程计构建了一套组合定位系统,单机具体性能见表2。行车中约1000 s时开启GMNS信号,约1500 s时关闭信号,约3500 s时再次开启,直到终点。比较开启与关闭GMNS信号期间的定位精度,验证即插即用功能。
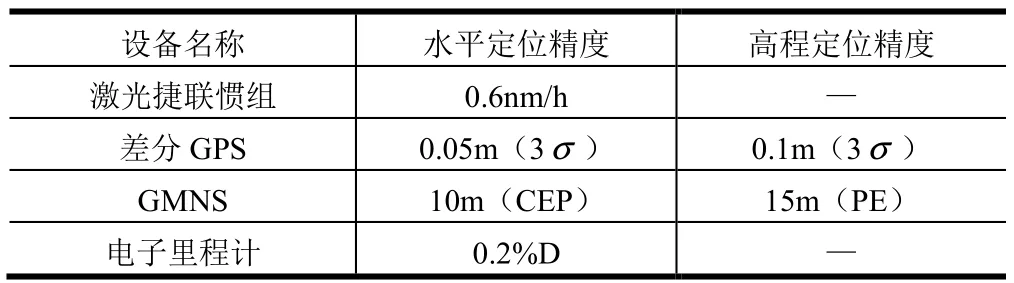
表2 实车试验设备条件Tab.2 Test Conditions
将该组合定位系统安装在猎豹试验车上,行车路线如图10所示,全程约44 km,行驶过程中以差分GPS的定位结果为基准,每3~4 km记录定位结果,进行精度检测。
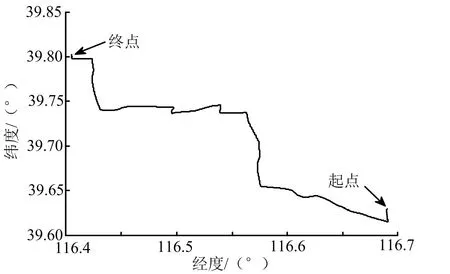
图10 跑车行驶轨迹Fig.10 Vehicle Trajectory Chart
行车中采集SINS、GMNS和里程计的原始数据,进行离线解算。
定位误差统计如表3所示。表3中1点位的测量位于1000 s之前,此时未开启GMNS信号,以INS/OD组合的方式进行定位,此间定位误差逐渐增大;2、3点位为1000~1500 s之间的定位点,此时开启GMNS信号,可观察到定位误差减小;4~8点位无GMNS信号,定位误差逐渐增大,高程定位误差变化最为明显;9~12点位开启GMNS信号,定位误差再一次收敛。

表3 定位误差统计Tab.3 Positioning Error Statistics

续表3
实车试验过程中 12个定位点的高程定位误差如图 11所示。从图 11可见,采用异步融合算法融合GMNS信号期间可明显提升组合定位精度。且使用过程中无误差突跳,定位精度可信度良好。

图11 实车试验高程定位误差Fig.11 Height Error Chart
异步多源组合定位算法有效融合了GMNS的非等间隔信号,行车中随机开启与关闭GMNS信号,定位功能不受影响,识别出了GMNS信号,利用了GMNS的有效信息,实现了定位信息源的“即插即用”。
6 结 论
提出的基于因子图的异步非等间隔组合定位算法避免了外推法带来的误差,利用了GMNS等信息源定位信息,更加准确地估计了惯导的水平轴陀螺零偏,抑制了定位误差的发散,提高了定位精度。
异步融合算法中,量测信息“即来即更新”,实现了定位信息源的即插即用,进一步增强了定位系统的可靠性,提高了陆基机动武器系统的实战化水平。

