基于前景理论的众包物流配送方行为决策演化博弈分析
——基于发货方视角
李 玉, 吴 斌, 王 超
(南京工业大学 经济与管理学院,江苏 南京 211816)
0 引言
众包物流为物流行业“最后一公里”问题提供了一个创新性的解决方案。所谓众包物流是指把原本应该由企业员工承担的配送工作,以自由自愿的形式转交到企业外的大众群体来完成。在该系统中,由于信息不对等,如配送方故意夸大自己的实力、缺乏责任感等,导致货物在配送过程中出现受损、丢失、延迟等问题。由于个体的本性都是自私的,发货方若想降低安全风险,就必须了解哪些因素影响了配送方的行为决策,并采取有效的应对方法。
Wang等人[1]首先提出了利用大量闲散的城市居民,来实现实时物流配送优化,即众包模式来解决城市物流“最后一公里”问题;Lin等人[2]通过比较三种常见的配送方式,发现众包配送具有成本费用低、环境友好等优势。国内学者就众包物流的安全与监管问题进行了大量的定性研究。有人认为众包物流就是快递版的Uber,其安全性问题的解决直接关系到该模式能否可持续发展。已有的研究分析了众包模式的影响因素、激励机制与风险控制,发现预期收益、努力期望、激励机制等因素会对大众参与众包的行为产生影响[3~5]。Baruch等人[6]研究了影响参与者加入众包平台的动机以及障碍等问题,结果发现任务的完成质量是参与者关注的重点。刘戌峰等人[7]则利用演化博弈方法定量研究外包知识共享行为的影响因素。对于众包项目中存在的风险,Liu等人[8]指出众包工作者的风险(能力、态度等)、工作者与发包者之间的关系风险、任务风险等都对众包的完成结果产生消极的影响。针对参与者加入众包的影响因素,国内外学者进一步就如何提高众包工作者努力水平进行了深入研究。Duan等人[9]根据众包工作模式的连续性,分别设计了两种竞拍激励机制来确保移动用户用真实值竞价。Wang等人[10]针对移动众包系统提出了一种基于隐私保护的激励机制,通过更新众包工作者的声誉等级来降低移动众包中的“free-riding”和“false-reporting”问题。郝琳娜等[11]则从定量与定性角度研究如何建立众包社区的信誉评价机制与诚信保障机制。
综上所述,目前的研究主要存在以下问题:(1)关于众包模式参与者行为已有研究,但关于众包物流参与者决策研究的文献较少。仅有Punel等人[12]通过分析531份众包配送调查问卷,得出配送者的经验以及配送任务的类型会对参与者的选择行为产生显著影响。与文献[12]不同,本文构建了演化博弈模型,对参与者的行为进行定量分析。(2)现有的研究都是基于参与者是理性人角度出发,并未考虑到个体的有限理性特征。(3)市场主体的风险管控机制与众包参与者的努力水平不一定成正相关关系。鉴于以上几点,本文将前景理论引入到演化博弈中,考虑发货方与配送方的利益相关性,研究提高众包物流配送方努力水平的条件与影响因素,并进一步探讨保价制度对于配送方努力水平的具体影响,以及该制度下如何降低众包物流的安全风险。
1 模型建立
1.1 模型假设
在不考虑外部环境及其他市场主体影响的情况下,众包物流配送过程中不安全问题是否发生可以视为是配送方与发货方的博弈结果,而博弈本身可以看成是风险决策行为。基于发货方与配送方的博弈关系,本文做出如下假设:
假设1博弈中只存在发货方与配送方这两类群体,且这两类群体中的个体都是有限理性的。个体策略选择主要依据自身对于策略得失的主观心理感受,而非实际效用情况。依据前景理论,将个体对策略得失的心理感受用前景价值v来表示,v根据前景理论的价值函数v(x)与权重函数π(p)来计算:
(1)
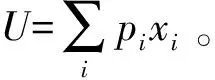
(2)
其中,α,γ∈(0,1)表示风险偏好与风险厌恶系数,决定博弈主体的风险偏好。当α=γ=1,表示风险中立。λ(λ≥1)表示损失规避系数,值越大博弈主体的损失规避程度就越高。
假设2参与众包的两个群体均只存在两种策略,其中发货方可选择监测或不监测配送方的行为,这里用行动集(监测,不监测)表示;配送方根据每次任务的奖金报酬、配送要求等决定配送行为,决策集为(努力,不努力)。
假设3考虑到众包物流的安全问题,博弈双方都要承担一定的安全风险,如货物损坏、丢失风险、信息泄露风险等,即双方的安全风险成本线性相关。若配送方承担的风险成本为C,则发货方承担的风险成本为kC,其中,k为风险传递系数。因为在博弈过程中,双方承担风险的比例是变动的,因此k的取值可能大于1,也可能小于1。
假设4博弈双方具有能力互补效应。在发货方选择监测,配送方选择高努力水平完成配送工作的时候,货物损失的风险最低。在不影响博弈结论的情况下,假设此时的安全风险成本为0;仅有一方进行监测,或者努力时,安全风险成本较高;当双方采取(不监测,不努力)时安全风险成本最大。
1.2 收益矩阵构建
结合上述四点假设,构建众包物流参与者决策博弈的收益矩阵如表1所示:

表1 众包物流参与者收益前景值矩阵
各参数含义如下:
Cs:发货方监测配送方付出的成本,表示对全部付出的价值感知(前景价值,下同),取值范围为(0,+∞)。
Ce:配送方认真工作付出的成本,表示其努力将货物送达目的地所花费的时间、劳动、和精力的价值感知,取值范围为(0,+∞)。
L1:配送方不努力,造成货物受损、丢失或者延迟完成受到的惩罚,表示配送方对损失的客户满意度、奖金等处罚的价值感知,取值范围为(0,+∞)。
L2:配送方承担的安全风险成本,表示将货物按时安全送达目的地过程中可能发生的货物破损等损失的价值感知,取值范围为(0,+∞)。
q1:当发货方监测,配送方不努力时,双方应该承担的安全风险成本的折扣系数,取值范围为[0,1]。
q2:当发货方不监测,配送方努力时,双方应该承担的安全风险成本的折扣系数,取值范围为[0,1]。
ps2:当双方采取(不监测,不努力)策略时,事故发生的概率。取值范围为[0,1]。
ps3:表示配送方不努力而受到惩罚的概率。取值范围为[0,1]。
(1)当双方采取(监测,努力)的策略时,由假设4可知此时的安全风险成本为0,因此发货方需要付出的成本为Cs,配送方需要付出的成本就是其努力工作带来的前景价值Ce。该情况下,出现事故的概率ps1=0。根据公式(1):Cs=π(1-ps1)v(cs)+π(ps1)v(0)=v(cs),同理,Ce=π(1-ps1)v(ce)+π(ps1)v(0)=v(ce)。
(2)当双方策略为(不监测,不努力)时,根据假设3可知,配送方承担的安全风险成本为L2,由于风险传递性,发货方承担的安全风险成本为kL2。此时,安全事故发生的概率是ps2,如果事故发生,则实际造成的损失为l2;若事故未发生,则配送方承担的安全风险成本为0,由假设1可得:L2=π(1-ps2)v(0)+π(ps2)v(l2)=π(ps2)v(l2)。
(3)当双方的策略为(监测,不努力)时,依据假设3,配送方受到的惩罚为L1,此外还需要支付的安全风险成本为q1L2;发货方此时的成本则是(Cs+kq1L2)。该情况下,安全事故可能发生的概率为ps3,如果发生事故配送方受到l1的罚款;如果不发生,那么配送方承担的安全风险成本为0,依据假设1:
L1=π(1-ps3)v(0)+π(ps3)v(l1)=π(ps3)v(l1)
(4)双方策略为(不监测,努力)时,配送方除了需要付出固有成本Ce,还需要承担的安全风险成本为q2L2,而发货方则需要承担的安全风险成本为kq2L2。
2 模型求解与分析
根据Friedman的演化博弈方法,基于表1,发货方选择“监测”或“不监测”策略的期望前景值、平均前景值为:
U1s=L1-kq1L2-Cs-L1y+kq1L2y
(3)
U1n=(1-q2)kL2y-kL2
(4)
U1=xU1s+(1-x)U1n
(5)
同理,配送方“努力”和“不努力”的期望前景值与平均前景值为:
U2s=q2L2x-Ce-q2L2
(6)
U2n=(1-q1)L2x-L1x-L2
(7)
U2=yU2s+(1-y)U2n
(8)
根据Malthusian动态方程,即策略的增长率等于它的相对适应度,只要采取该策略的个体适应度比群体的平均适应度高,那么这个策略就会增长[13]。由此可以得到众包物流发货方的复制动态方程:

=x(1-x)[L1-Cs+(1-q1)kL2-L1y+(q1+q2-1)kL2y]
(9)
得配送方的复制动态方程:

=y(1-y)[L1x+(q1+q2-1)L2x+L2-Ce-q2L2]
(10)
2.1 平衡点计算
根据发货方与配送方的复制动态方程,联立得到由发货方与配送方构成的二维动力系统J为:

(11)

命题1该二维动力系统J的平衡点为(0,0),(0,1),(1,0),(1,1),(x0,y0)。

2.2 平衡点稳定性分析
由于众包物流双方多是社会闲散群体,目前经常出现众包物流安全事故,因此无论是发货方还是配送方都应该尽力减少事故的发生概率,实现众包物流的稳定发展。由动态方程组求出的平衡点不一定是系统的演化均衡策略(ESS),根据Friedman提出的Jacobian矩阵的局部稳定性[13]可得:
其中:a11=(1-2x)(A-yB),a12=x(1-x)B,a21=y(1-y)C,a22=(1-2y)(Cx+D),detJ=(1-2x)(1-2y)(A-yB)(Cx+D)-xy(1-x)(1-y)BC,trJ=(1-2x)(A-yB)+(1-2y)(Cx+D)。
当矩阵满足:detJ>0,trj<0时,局部均衡点将成为演化均衡点(ESS)。通过计算可以得到四个均衡点处a11,a12,a21,a22取值。如表2所示

(12)
这四个条件同时满足时,系统收敛于(1,1),也即(监测,努力)决策集,系统的安全风险成本最低。

表2 局部均衡点处a11,a12,a21,a22稳定性分析
命题2(x0,y0)不是系统的演化均衡点。
证明只有当detJ>0,trJ<0时,局部均衡点才是演化均衡点(ESS)。在点(x0,y0)处,a11=0,a22=0,显然trJ=0。因此该分析方法失效,文献[15]运用微分分析法进行判断。将式(9)、(10)进行对x,y求微分并带入(x0,y0)。得:
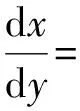
[(q1+q2-1)kL2-L1]
(13)

[(q1+q2-1)L2+L1]
(14)

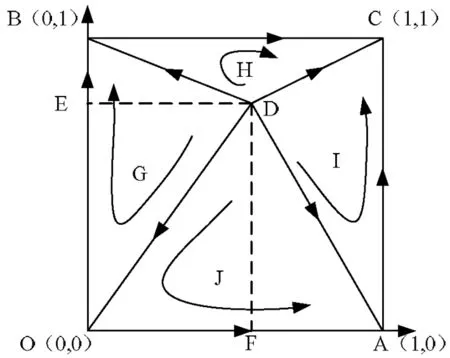
图1 动态演化博弈相位图
2.3 模型分析
由式(12)可以得出以下几点结论:
(1)前两个约束条件表明,发货方监测配送方的成本Cs不能大于其惩罚的期望收入与监测之下的安全效益之和。同时,Cs也不能大于在(监测,努力)决策下所获的安全效益。后两个约束条件表明,配送方努力工作的成本Ce不能大于其对惩罚成本的前景值与发货方监测下的安全风险之和,同时不能大于在策略(不监测,努力)下所获得的安全效益。然而事实上,参与众包物流的双方都是有限理性的,在现实情况中都是凭直觉进行决策,不能最大化利用现有信息,导致其行为产生系统性偏差。
(2)在风险决策过程中,人们经常偏离完全理性,由前景理论可知,在面对损失时,有限理性决策者经常是呈现风险偏好的特点。配送方努力工作需要付出成本Ce,发货方监测也需要付出成本Cs;而选择不监测以及不努力策略虽然会有一定的概率发生事故,造成损失L2以及惩罚损失L1,但是此时的决策参与者是风险偏好性的,宁可选择冒险也不愿意承担这些确定性的损失,由此可知,众包物流出现安全漏洞的现象确实时有发生。
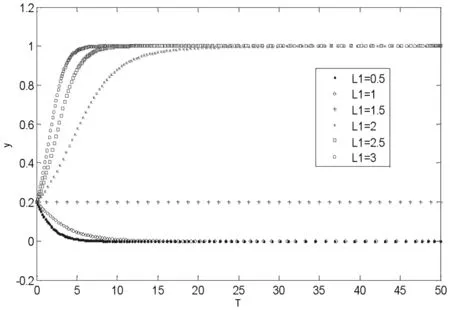
(3)显然,第二点结论与前面约束条件不相符。究其原因,众包物流多为同城配送,致力于解决“最后一公里”配送问题。同城环境容易造成参与者过度自信,发货方以及配送方都会在一定程度上低估事故发生的概率以及被惩罚的概率,即π(ps2) 综上所述,众包物流的参与者都倾向于风险偏好,这就极有可能导致众包物流安全事件的发生,难以达到系统的演化均衡点(监测,努力)策略。因此,尝试引入与配送方努力成本Ce以及责任风险成本L2相关的变量——保价金Br。通过在保价金制度下的发货方以及配送方的价值感知来剖析配送方的行为决策,进而提出有效的众包物流安全管理对策。 设配送方不努力的收入为Ir,参考点的收入为I0,保价金额为Br,配送方不努力而导致出现安全事件被惩罚的概率是pe,若被发现,则按照βIr进行惩罚,β为惩罚系数(包含由于不努力造成的顾客满意度、声誉、预期收益的贴现损失),假设配送方的收益与损失均可以货币化。由前景理论构建保价制度条件下配送方决策行为模型: maxV(Ir)=π(1-pe)v(Ir+Br-I0)+ π(pe)v(Br-βIr-I0) (15) 由公式(15)可以看出,配送方的收益与损失是基于参照点确定的,价值函数由收益与损失组成,根据前景理论,配送方对于收益,是风险厌恶型,而对于损失则呈现风险偏好。现实生活中,众包配送任务类型的不同,导致发货方的保价金额存在差异。 从保价条件下配送方行为决策模型可知,配送方不努力的行为将会影响其总收入,进而对其主观心里感知的前景价值造成影响。通过数学推导,将会得到一些有利于众包物流安全管理的结论。过程如下: 结合前文的假设条件,配送方不努力但未被惩罚的收入为:s1=Ir+Br-I0,被惩罚时的收入是:s2=Br-βIr-I0,则有: V(Ir)=π(1-pe)v(s1)+π(pe)v(s2) (16) 对公式(16)两边取全微分并化简得: (17) 又因为s1-s2=(1+β)Br,令m=(1+β)Br,则公式(17)可以变形为: (18) (19) (20) (1)当N(s2)=N(s1)时,公式(20)的值为0,配送方的绝对风险规避系数N(s)不变,也就是配送方对于众包物流安全风险的态度不变,未能达到增强安全管理,防止安全事件发生的目标,也就是保价Br对于配送方的努力水平没有任何实质性的影响。 (2)当N(s2)>N(s1)时,公式(20)大于0,则配送方的绝对风险规避系数N(s)递减,也就是配送方为风险偏好者,可能挑选保价金额更大的任务去完成,同时通过降低努力成本,例如“free-riding”[10]等方式获取更多的订单以及收益,此时保价Br的增加反而助长了其侥幸心理的行为产生。 (3)当N(s2) 综上所述,基于同样的处罚系数和监测水平,随着保价Br的增加,配送方可能会从风险中立演化为风险偏好或者风险规避。因此,发货方无法确定在哪种情况下保价的设立可以降低安全风险。假设配送方会适当选择不努力行为收入Ir以达到收入最大化。由公式(16)得: (21) 这表明,在保价条件下,可以采取以下两种方式: (1)当pe一定时,增加β,即在发货方的监测水平一定的情况下,必须加大对配送方出现安全事故的惩罚,才能减少安全问题的发生。如图2所示,不同的处罚风险感知对于配送方行为决策的影响。从演化图中可以看出,在值1.5附近存在某个临界值,当L1小于该临界值时,y收敛于0;当L1大于该临界值时,y收敛于1,并且L1的增加能使其更快收敛于1。因此提高配送方的处罚风险感知确实能影响其策略行为,促使其选择努力工作。 图2 不同惩罚风险感知条件下配送方决策行为演化图(Ce=1,Cs=1,k=1,q1=0.6,q2=0.4,L2=1) (2)当β一定时,增大pe,即在惩罚力度一定的情况下,必须加大对配送方努力水平的监测,及时反馈,可以让配送方不敢懈怠或是存在侥幸心理,以减少安全事故的发生。如图3所示,发货方选择不同的监测比例对于配送方行为决策的影响。从演化图3中可以看出,在值0.8附近存在某个临界值,当x小于该临界值时,y收敛于0;当x大于该临界值时,y收敛于1,并且x的增加能使其更快收敛于1。因此加大对于配送方的监测力度确实能影响其策略行为,促使其选择努力工作。 图3 不同监测比例条件下配送方决策行为演化图(Ce=1,Cs=1,k=1,q1=0.6,q2=0.4,L2=1,L1=0.5) 根据众包物流的研究现状,本文将前景理论引入演化博弈中,构建了参与方感知收益矩阵,推理得出配送方努力工作的条件以及影响配送水平的指标。考虑到个体的有限理性以及众包物流参与者之间的利益相关性,进一步分析保价条件下配送方的行为演化规律,并运用数值仿真技术进行验证。 根据理论推导,本文针对众包物流配送方的努力行为提出如下几点管理建议: (1)众包物流平台必须建立合理的双边收费策略与监管机制。合理的收费策略将针对任务的类型对发货方进行收费,并将收益合理奖励给配送方,这将有效降低配送方的努力成本前景值;同时,监管机制对配送方的配送过程进行严格管理,这将降低配送方的不努力成本前景值并对不努力的配送方实施有效处罚。 (2)优化众包物流平台的管理流程,有助于提高配送方的努力水平。对配送方设置较低的接入门槛,如不收取注册费等;平台的接单流程与用户交接流程的合理优化将有效节约配送者的时间成本。与此同时,平台必须加强配送方的沟通、培训工作,建立有效的沟通渠道,规范配送行为。 (3)合理的保价制度将有效提高配送方的努力水平。实际运行中,众包物流平台可以自由选择是否设置保价制度,一般发货方会根据自己的货物价值进行合理的保价。配送方趋于风险规避心理,合理的保价金额可以激励配送方发挥较高的努力水平进行配送工作;相反保价金额太高,配送方趋于风险偏好的心理,会进行针对性的挑选订单进行配送,同时通过搭便车等行为降低努力成本。因此,合理设置保价制度是控制配送方努力水平的关键。 (4)如果发货方与配送方不能认识到众包物流中监测的重要性与惩罚的严厉性,不能形成恰当的监测成本与努力成本的心理感知,即使众包物流的规范制度不断完善,也无法杜绝安全风险的产生。3 引入保价制度对配送方行为决策的影响分析
3.1 引入保价下配送方行为决策模型
3.2 保价金额变动对配送方行为决策影响分析


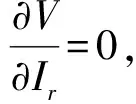

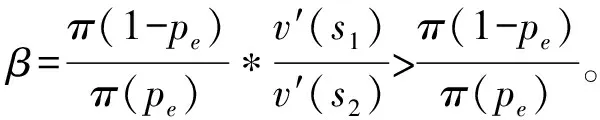
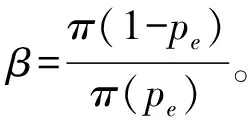

4 结论及政策建议

